
今回は、平面図形の「多角形の性質」について勉強します。
三角形、四角形は4年上で勉強しましたが、五角形、六角形、七角形、、、、とさらに角が多い図形もふくめて勉強します。また、4年下第3回では円と正多角形について習いました。正多角形は多角形の各辺の長さが等しい特別なものです。
「三角形の内角の和」、「三角形の外角の定理」など、今まで勉強した内容が出てくるので、ここでもう一度確認して使いこなせるようにしましょう。
また、面積の求め方の工夫では、面積を変えずに形を変える「等積変形」の問題が出てきます。
図形は、覚えることが意外に多いです。それぞれは難しいものではないのですが、問題の図形にどれがあてはまるか見つけるところがポイントです。問題を解くことでその感覚を身に付けましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
今回の内容で覚えることをカードにまとめました。
多角形の性質
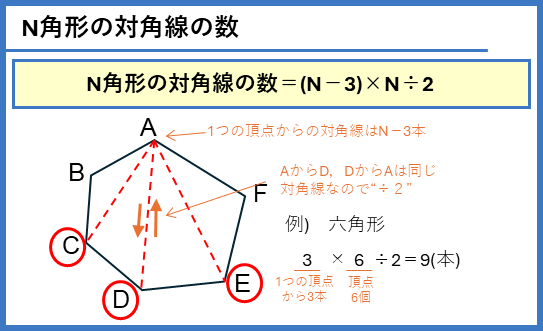
N角形の対角線の数
N角形の1つの頂点から引ける対角線は、自分と両どなりをのぞいた(N-3)本になることを理解しましょう。
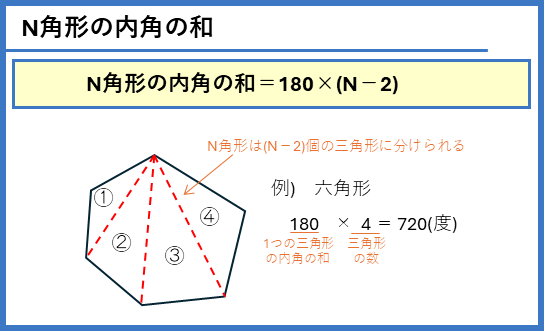
N角形の内角の和
N角形は、(N-2)個の三角形に分けられます。三角形の内角の和は180度なので、N角形の内角の和は、
N角形の内角の和=180×(N-2)
となります。式を丸覚えするのではなくて、三角形の分けて考えることを覚えましょう。
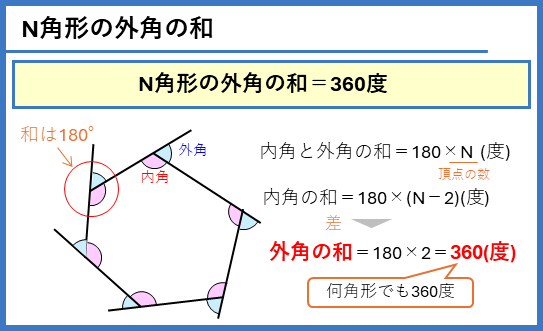
N角形の外角の和
N角形の外角の和は、どんな多角形でも360度になります。これはそのまま覚えてしまいましょう。
正多角形の1つの内角の大きさ
正多角形の1つの内角の大きさは、
多角形の内角の和÷頂点の数
あるいは、
180-1つの外角の大きさ (外角の大きさは、360÷N)
で求めることができます。この考え方をしっかり理解して覚えておけば、計算で求めることができます。

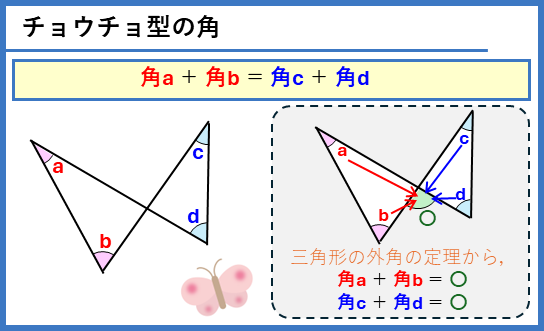
チョウチョ型の角
三角形の外角が同じであることから証明できますが、チョウチョ型として覚えて、図形の中から見つけられるようにしましょう。
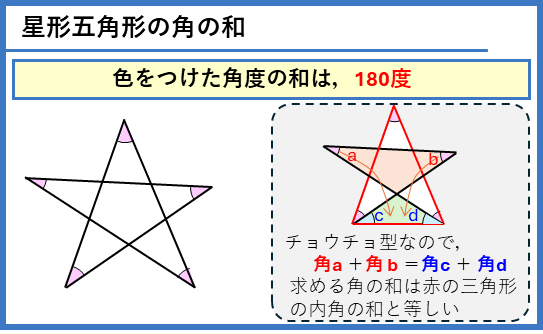
星形五角形の角の和
星形五角形の角の和は180度になります。チョウチョ型の2つの三角形を作ることで、1つの三角形の内角の和と等しくなることがすぐに分かります。補助線を引いてチョウチョ型の三角形の組を見つけられるかがポイントとなります。
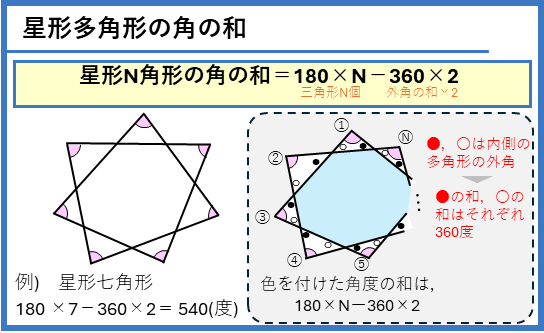
星形多角形の角の和
五角形以外の星型多角形の角の和は、
トンガリの三角形の内角の和の合計(180°×N)から、多角形の外角の和を2組分(360°×2)引いたもの
になります。上の星型五角形の角の和は、この考え方でも求めることができます。
面積の求め方の工夫
面積の等しい図形を見つける、作るー等積変形
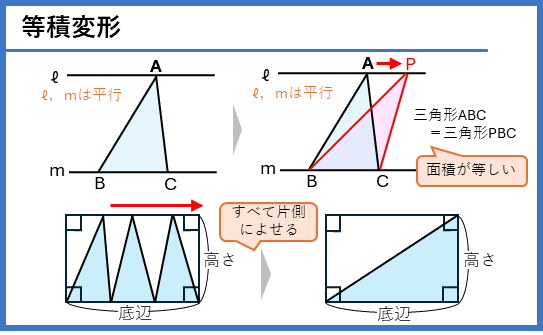
三角定規の三角形の特ちょうを利用する
三角定規の三角形は、正方形を半分にした直角二等辺三角形と、正三角形を半分にした30°-60°-90°の直角三角形になります。正方形の半分、正三角形の半分なので、次のような特ちょうがあります。
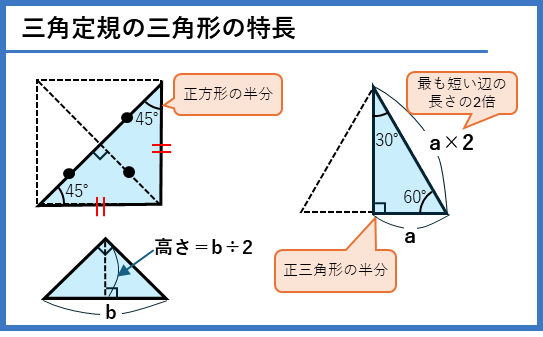
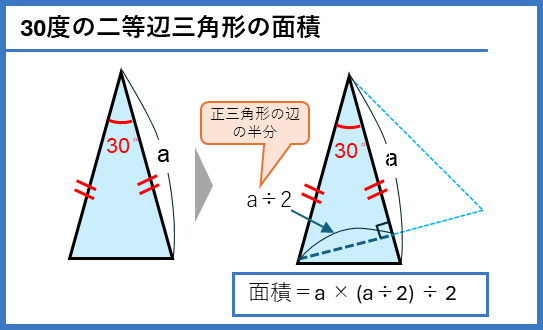
30°-60°の直角三角形の辺の長さの性質から、30度の二等辺三角形の面積を求めることができます。このように30度の三角形を見つけることで、高さを求めることができる場合があります。問題の図形から30度を見つけることが、ヒントになるかもしれないので、覚えておきましょう。
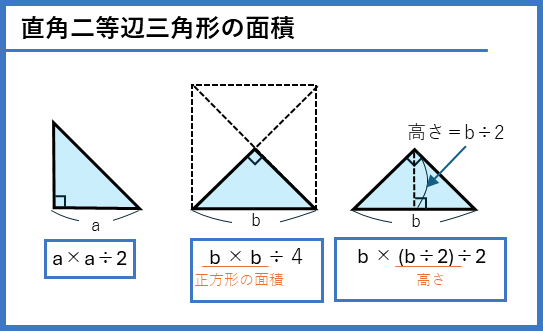
直角二等辺三角形は、長い辺でも、短い辺でも、どちらの長さが分かれば面積を求めることができます。
練習問題
正多角形の内角と二等辺三角形
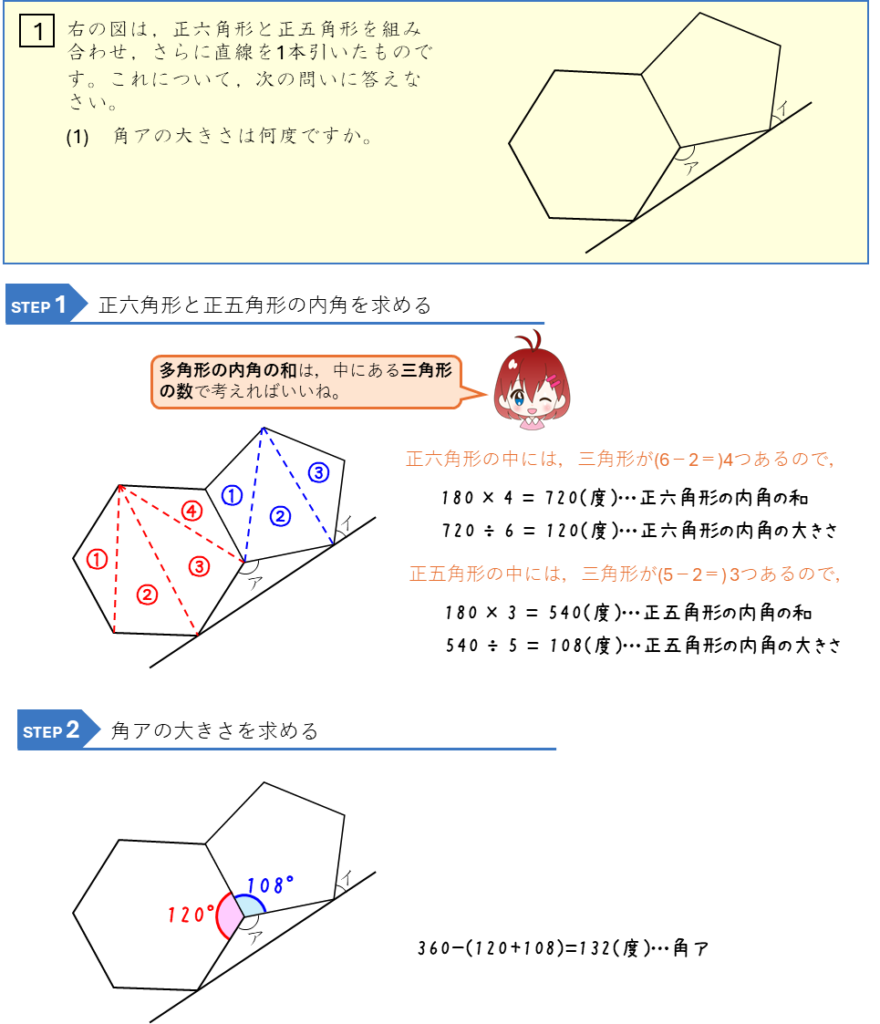
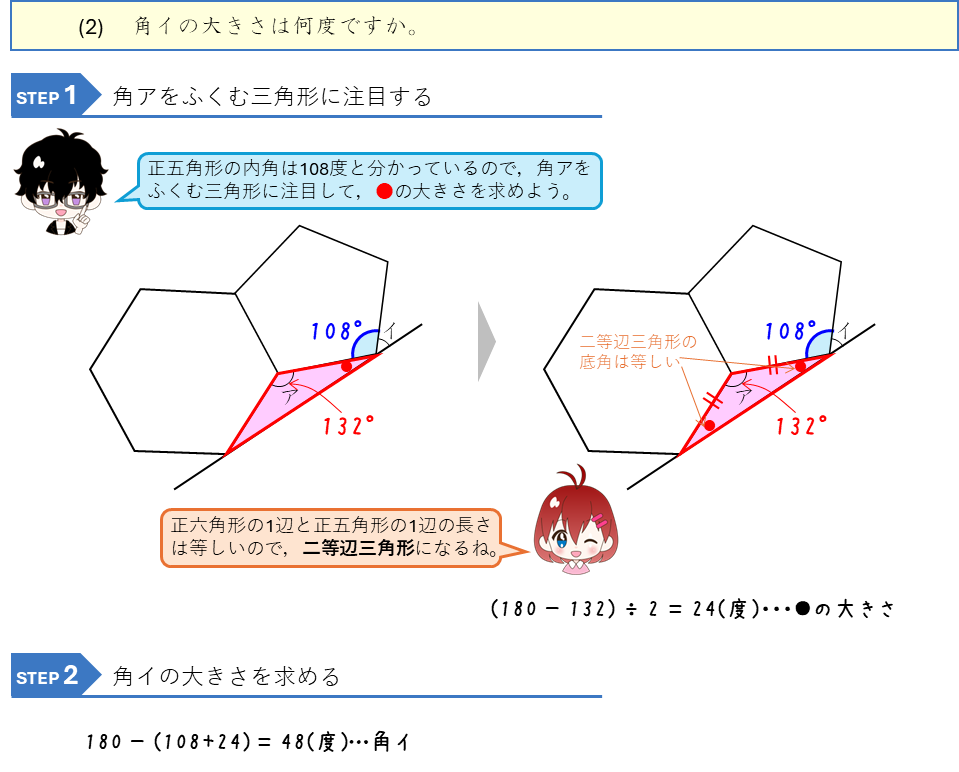
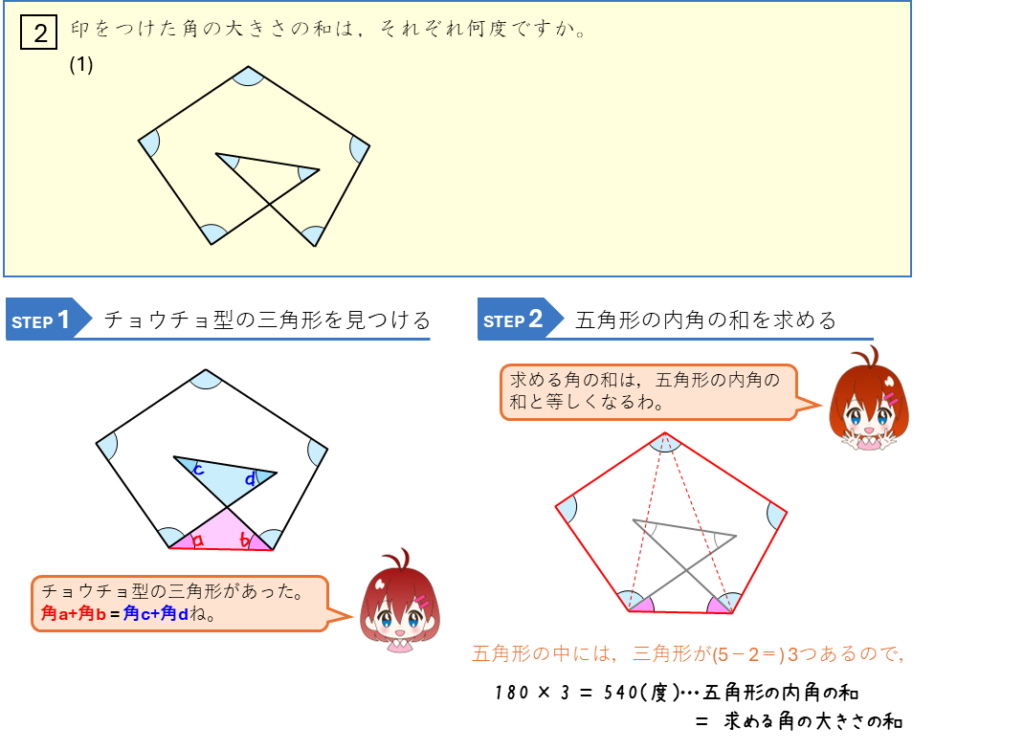
くぼんだ多角形の角の和
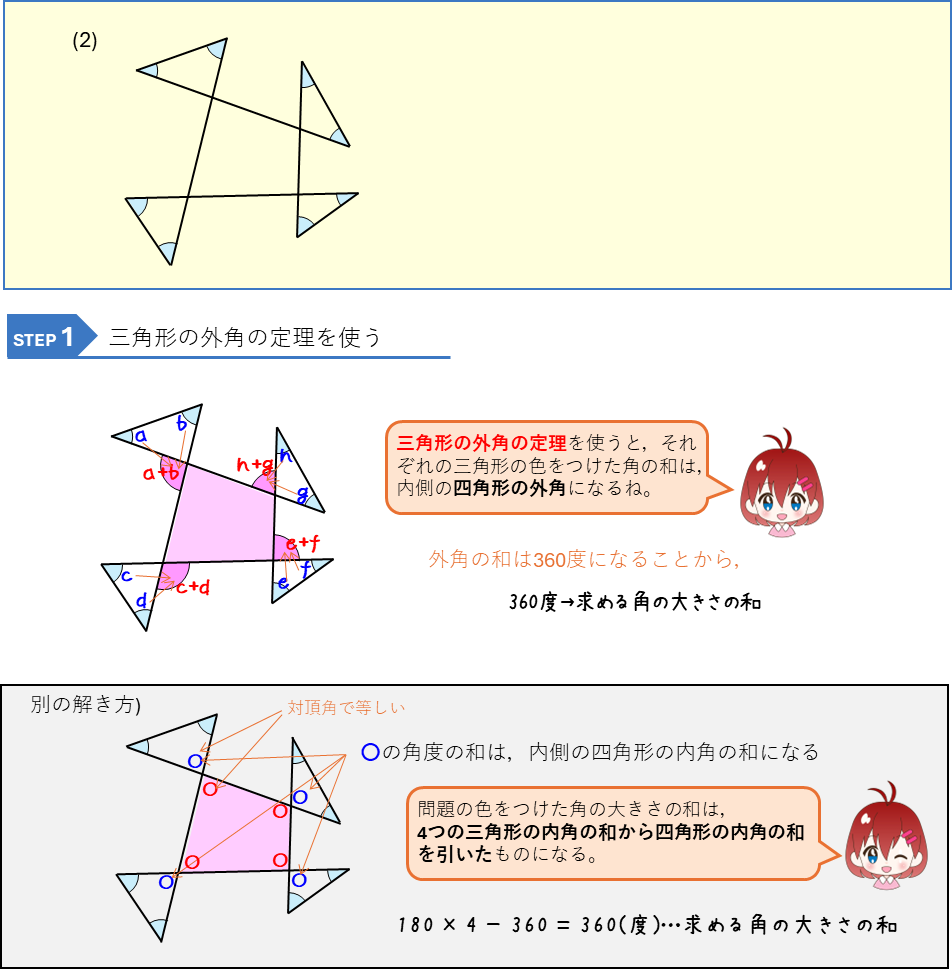
風車型の角の和
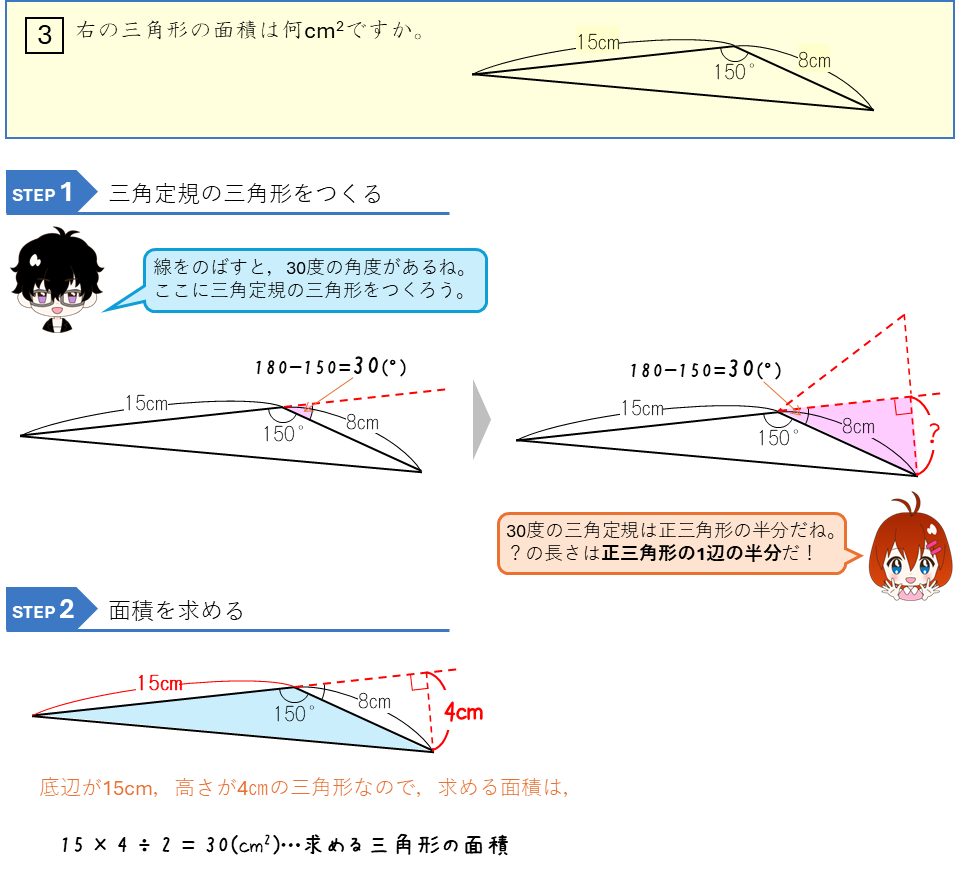
30度の直角三角形
等積変形ーのこぎり型
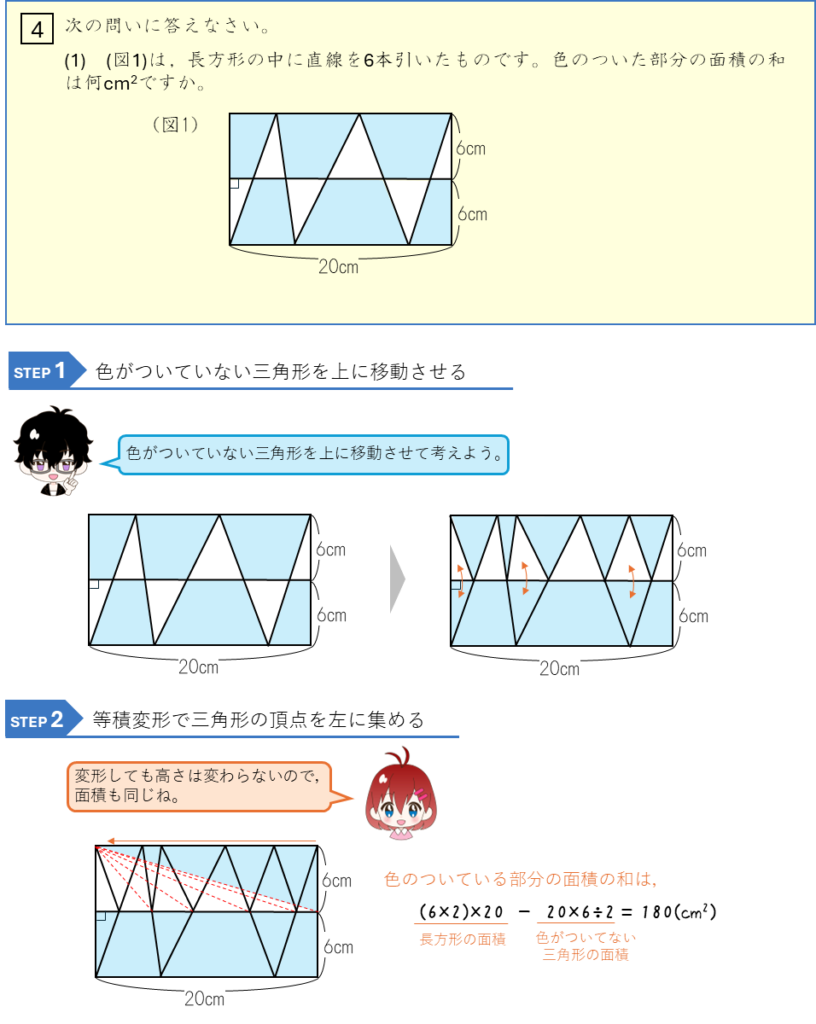
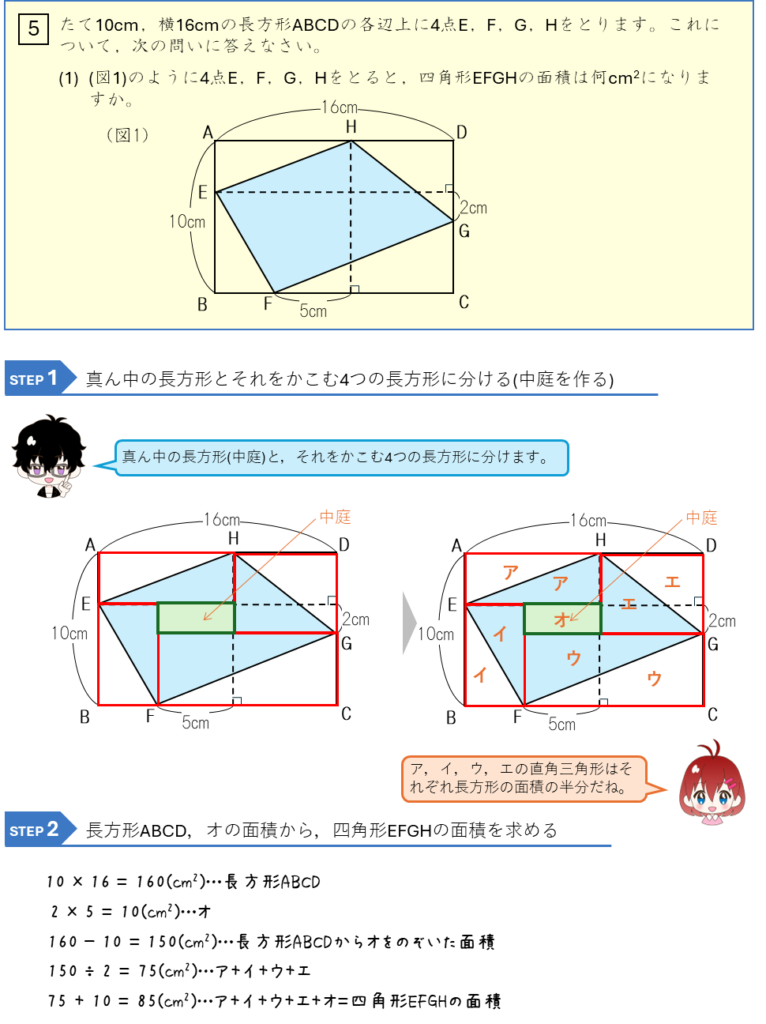
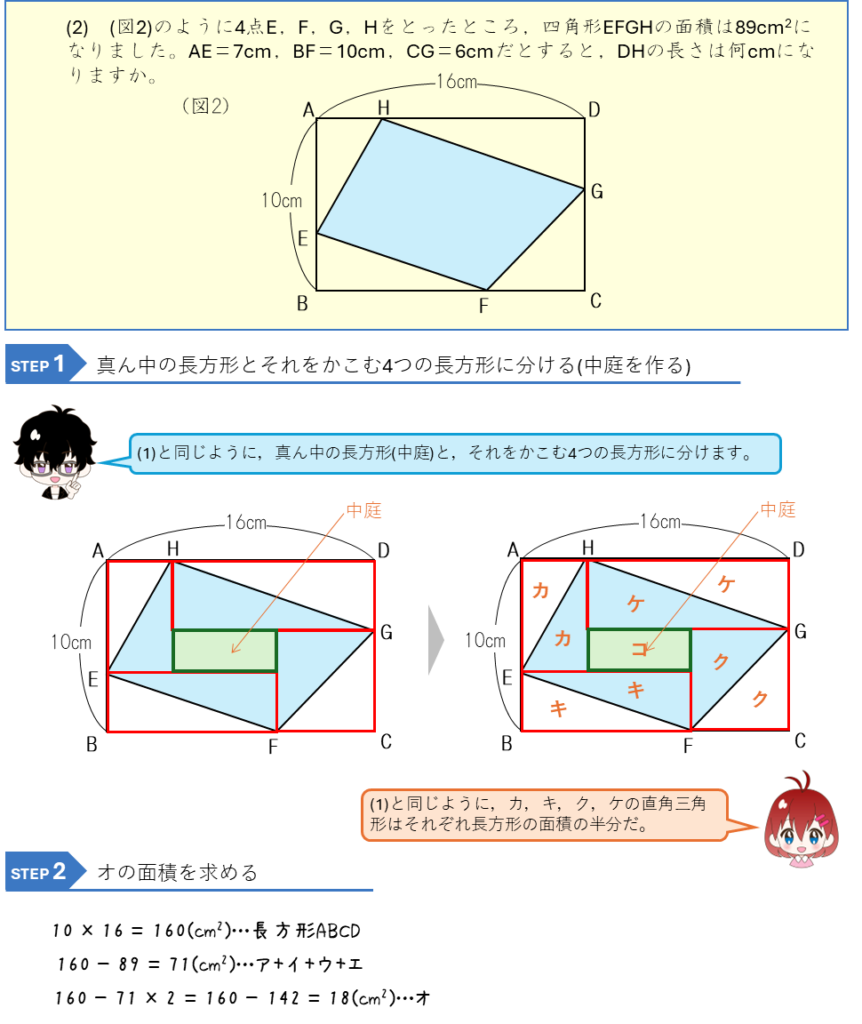
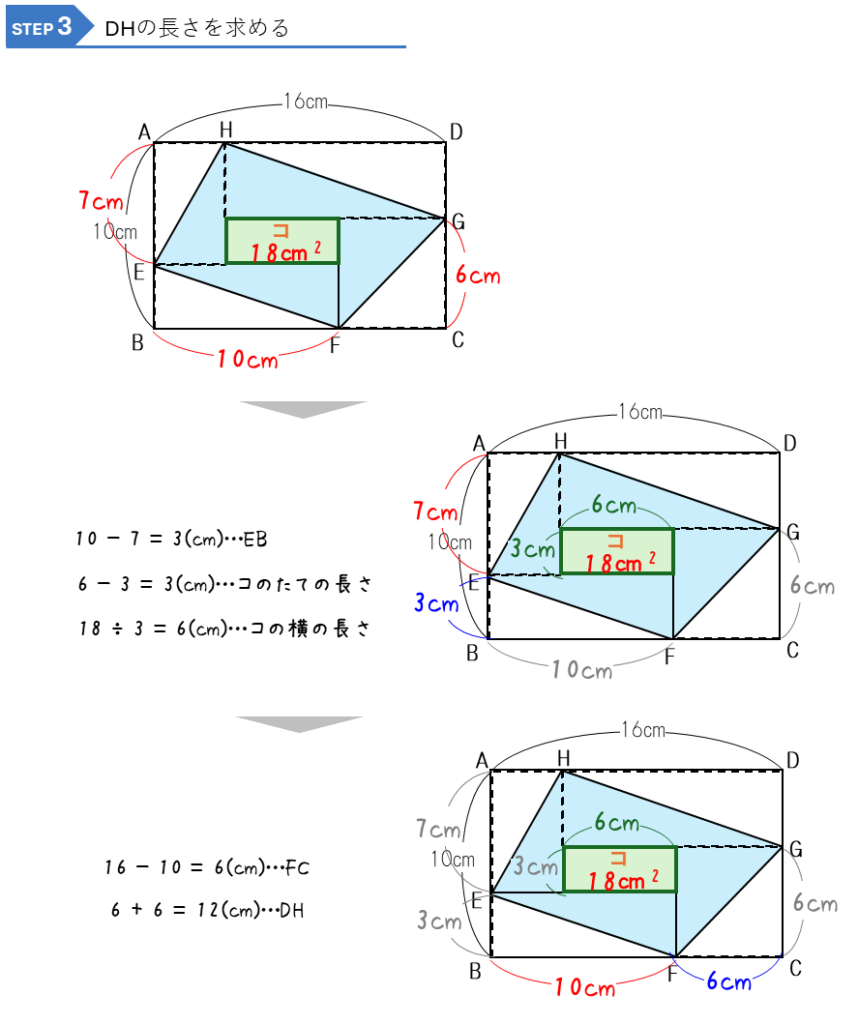
長方形の中の四角形

コメント