
今回は、平面図形の「図形の移動」について学習します。五年上第8回、第9回の「多角形の回転・転がり」、「円の回転・転がり」の復習と、新しく「おうぎ形の転がり」に取り組みます。
また、図形の向きを保ったまま、一定の方向に「すべらせる平行移動」についても学びます。2つの図形が重なる問題では、重なる部分が変化するポイントを意識して解いていきます。
これらの問題では、正しく図をかくことがとても大切です。作図のポイントをしっかりおさえて、図をかけるようにトレーニングしましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
多角形の転がり移動(復習)
多角形の転がり移動では、回転の中心を意識して作図していきます。
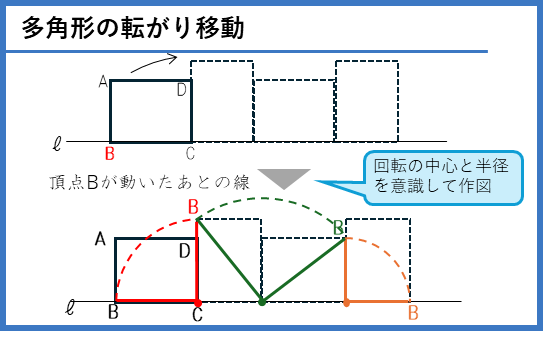
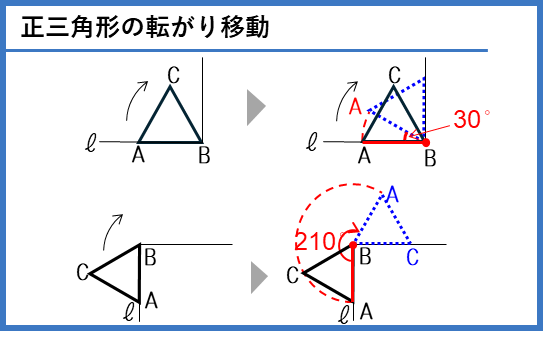
正三角形が、角の内側や角の外側を転がる場合です。
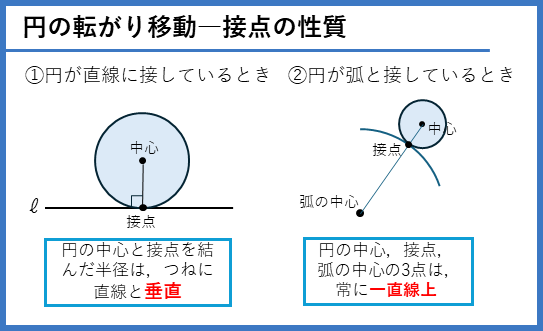
円の転がり移動(復習)
円の接点の性質の復習です。円の転がり移動などの基本となるので、しっかり覚えておきましょう。
円の転がり移動のポイントです。
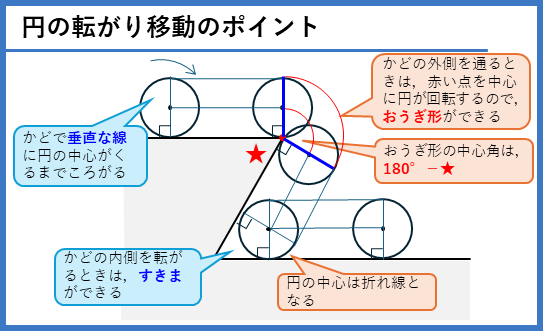
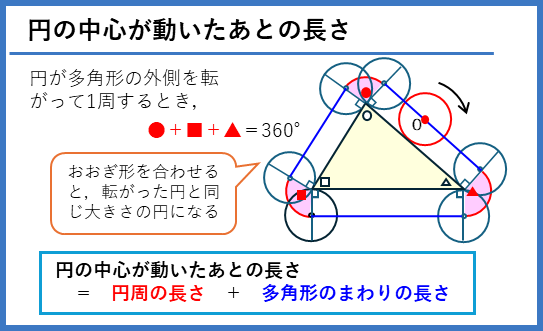
円が(へこみのない)多角形の外側を回転したとき、円の中心が動いたあとのおおぎ形は、それらの中心角の和が360度になります。下の図では、三角形の例ですが、他の多角形でも共通して成り立ちます。したがって、
円の中心が動いたあとの長さ = 回転する円の円周の長さ + 多角形のまわりの長さ
になります。
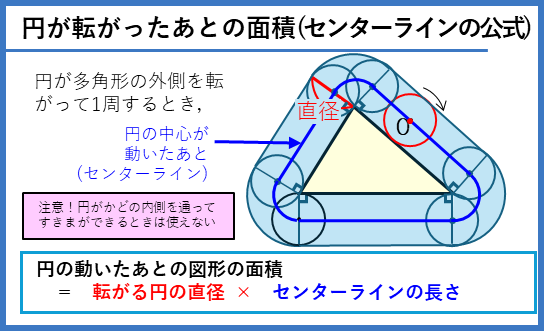
円の中心が動いたあとの長さが分かると、円が転がったあとの面積は、次の「センターラインの公式」で求めることができます。
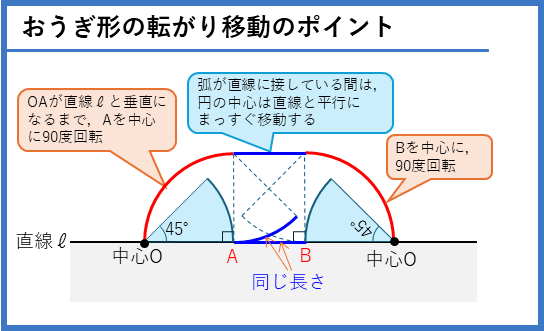
おうぎ形の転がり移動(New!)
おうぎ形の転がり移動では、弧が直線に接している間は、円の中心は直線と平行に移動します。
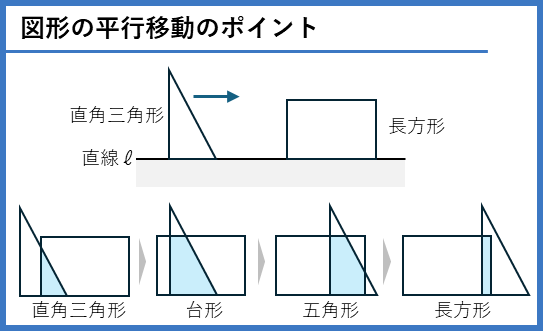
図形の平行移動(New!)
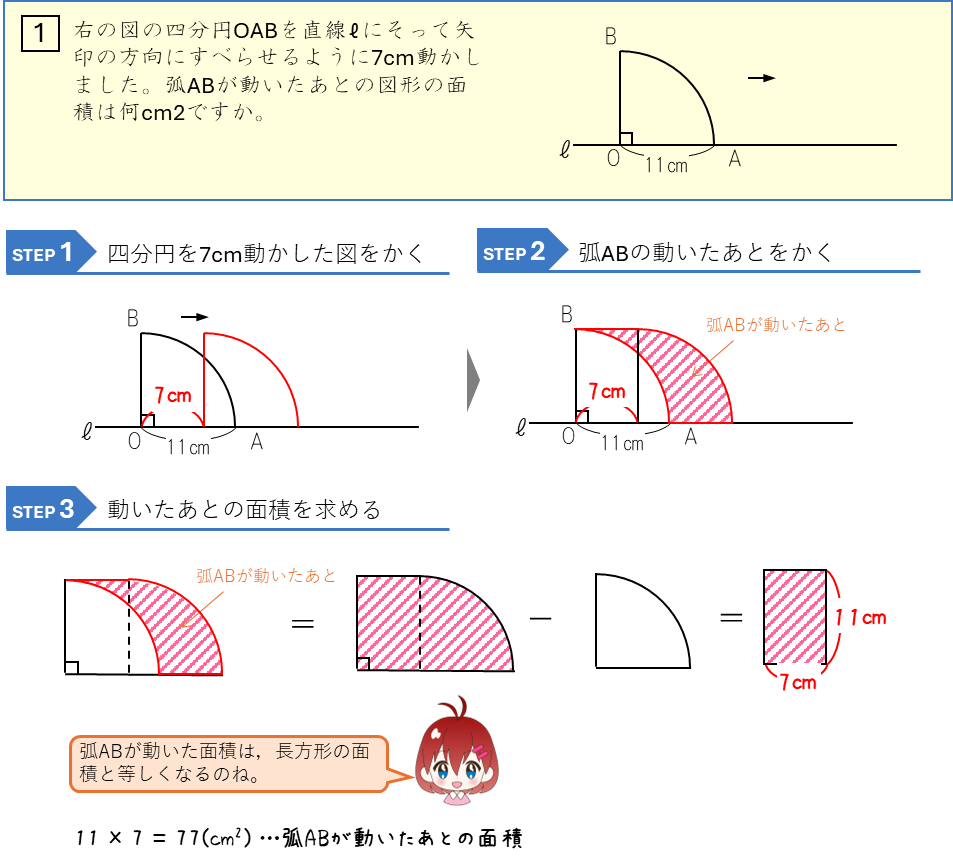
図形が向きを保ったまま、一定の方向にすべらせる平行移動では、2つの図形の重なる部分の形や面積を求める問題が出ます。直角三角形と長方形の場合は、重なる部分の形が、直角三角形、台形、五角形、長方形と変化します。図をかいて確認しましょう。
練習問題
図形の平行移動ー弧が動いたあとの面積
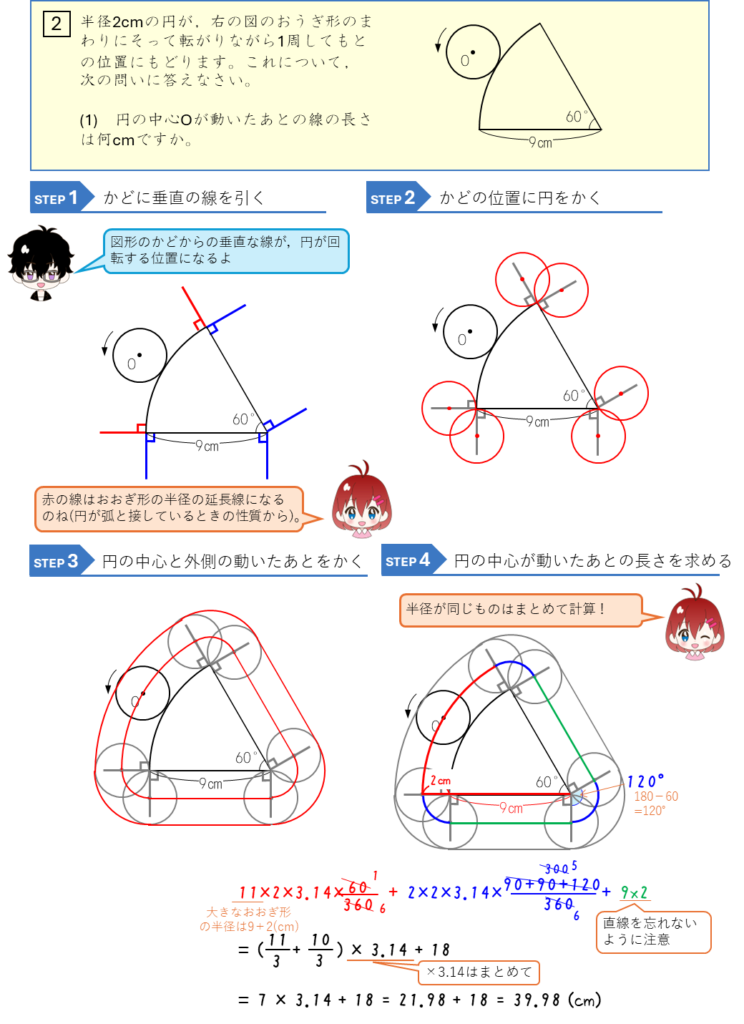
おうぎ形のまわりを転がる円

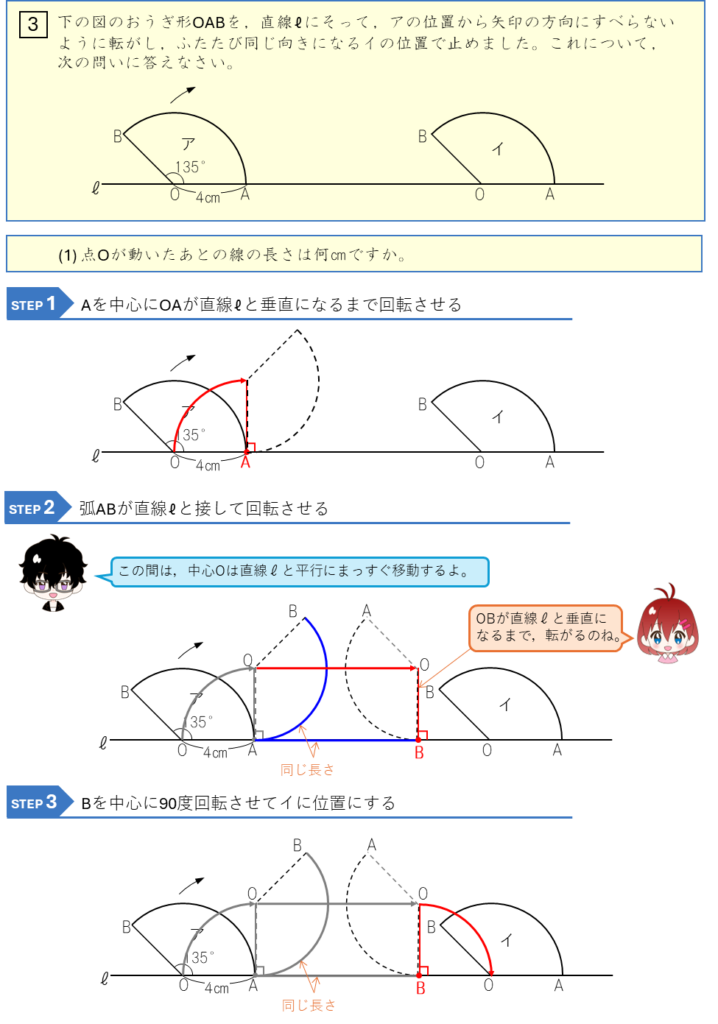
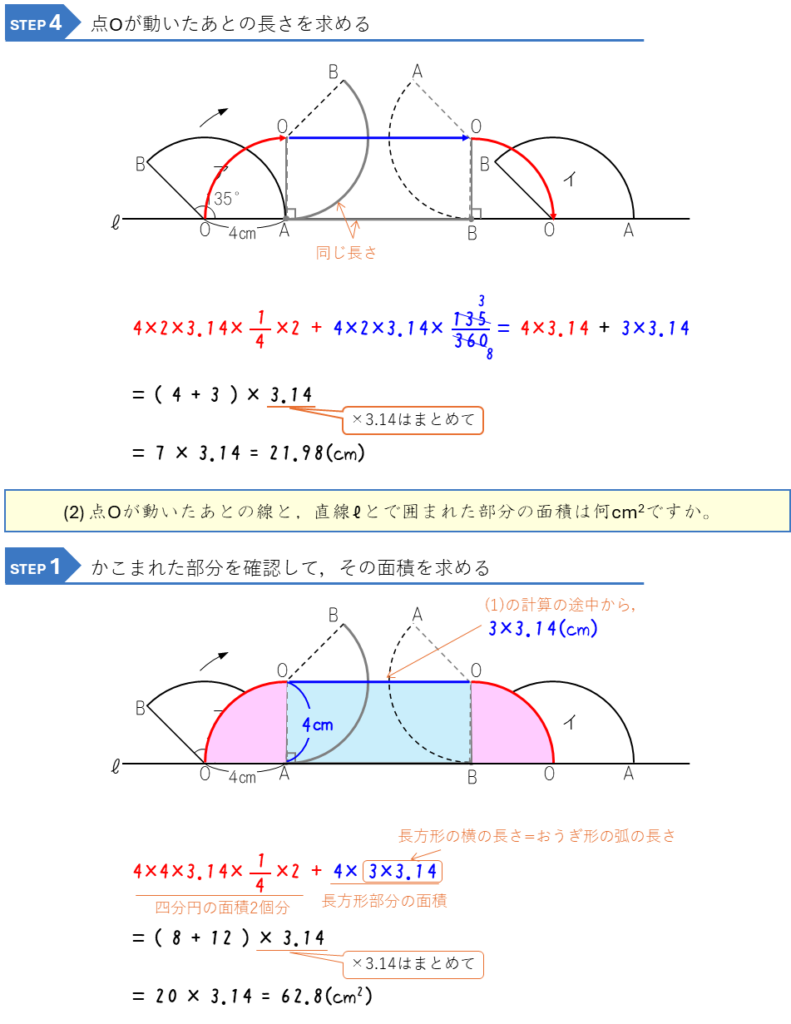
おうぎ形の転がり移動
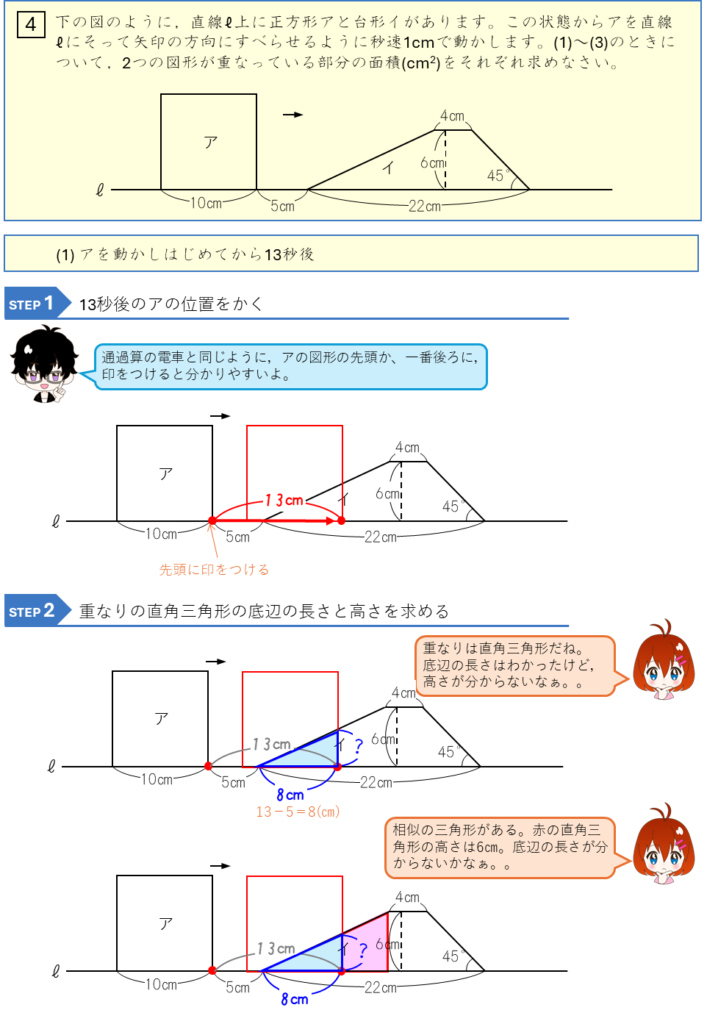
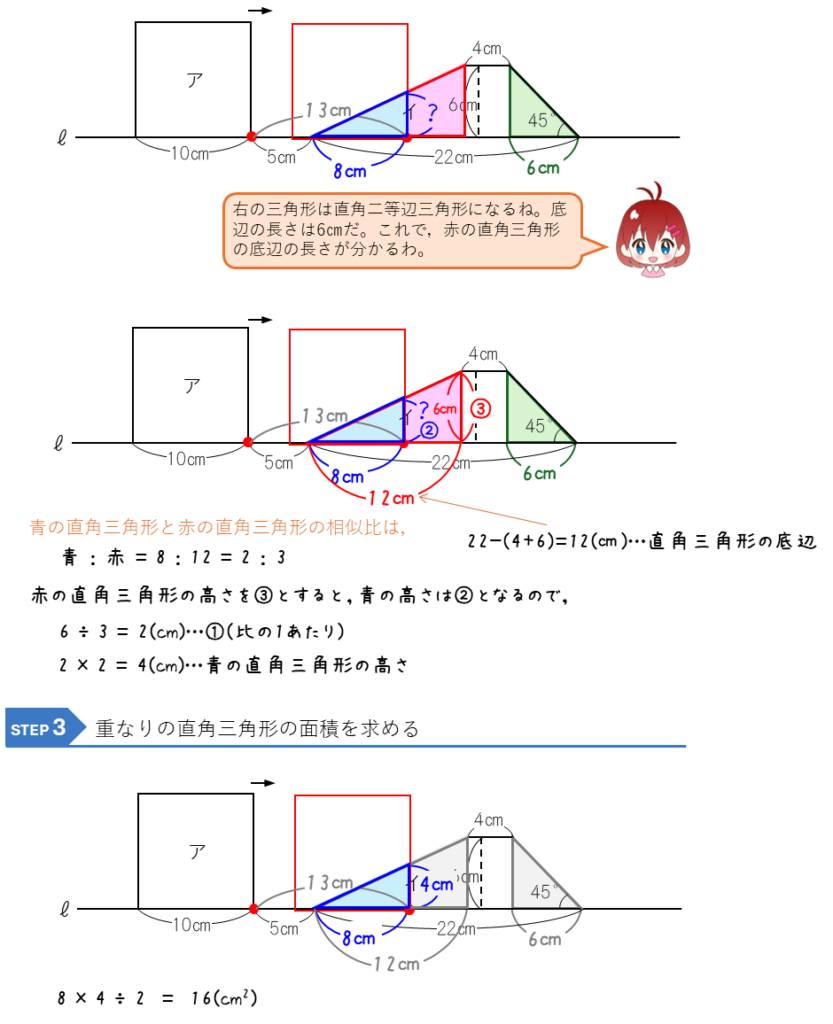
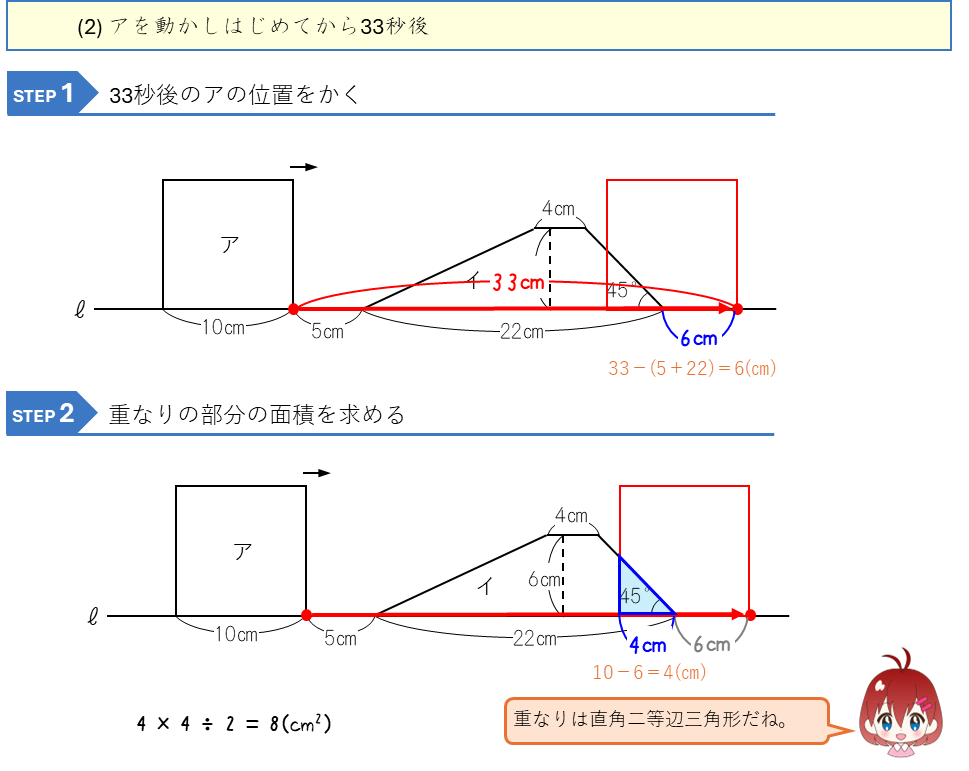
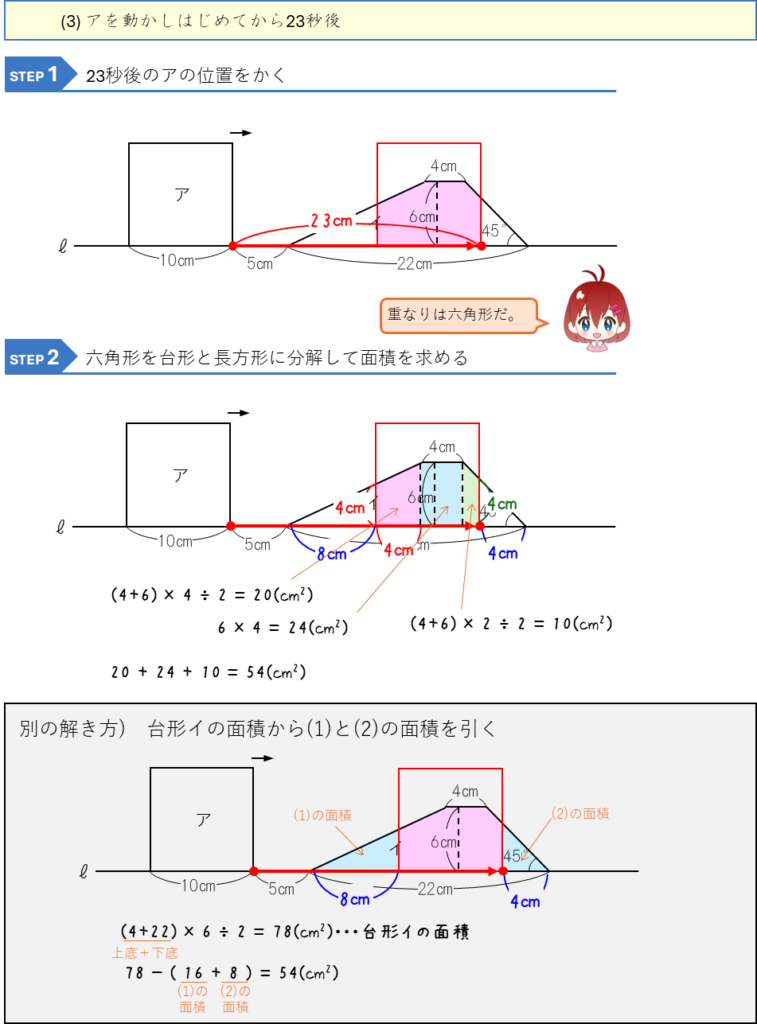
図形の平行移動ー正方形と台形の重なり
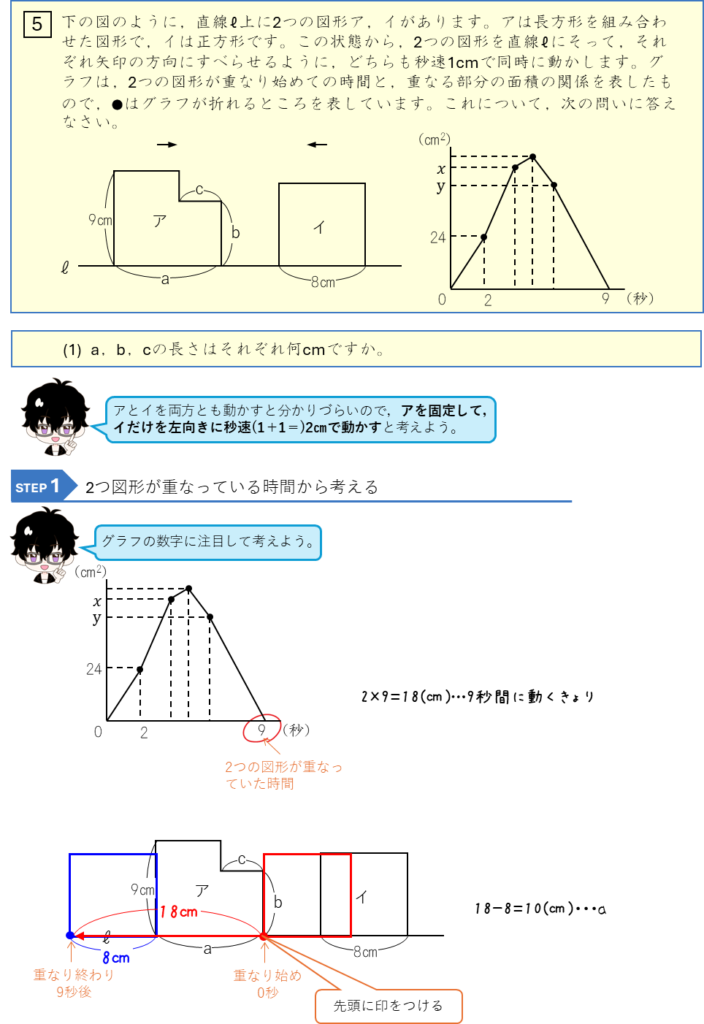
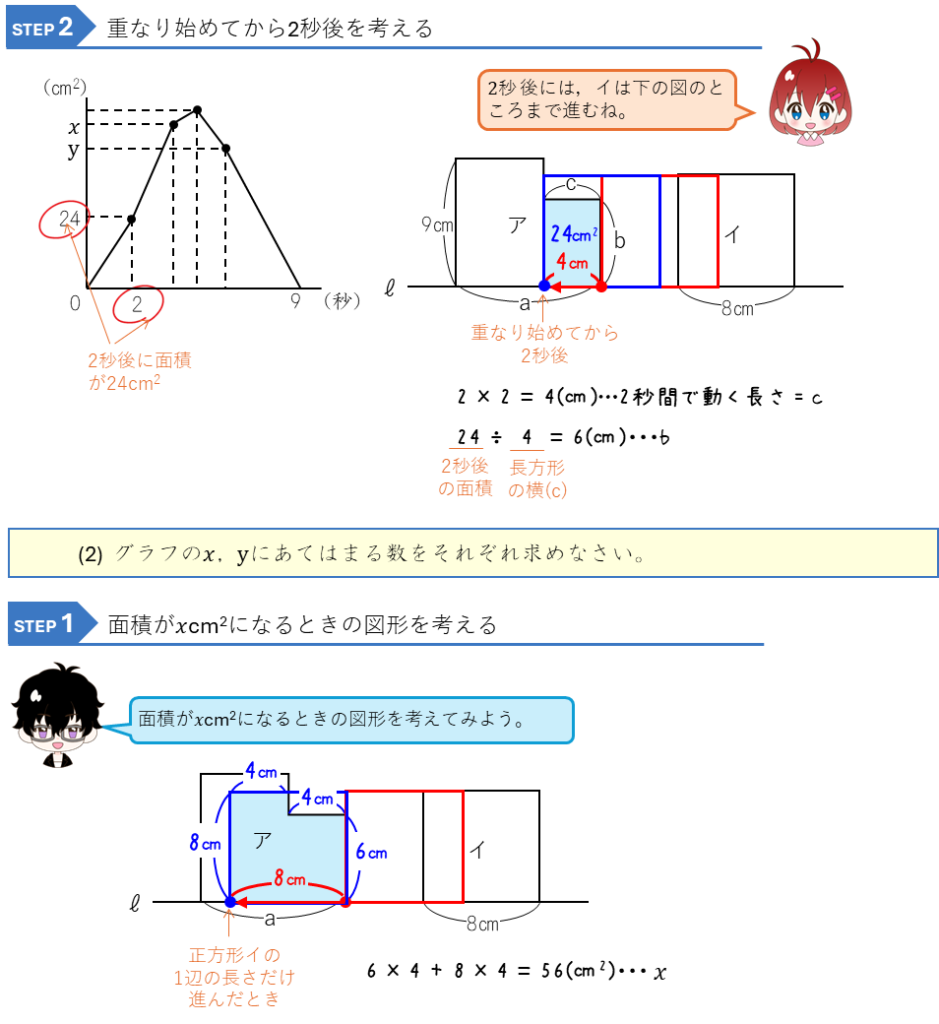
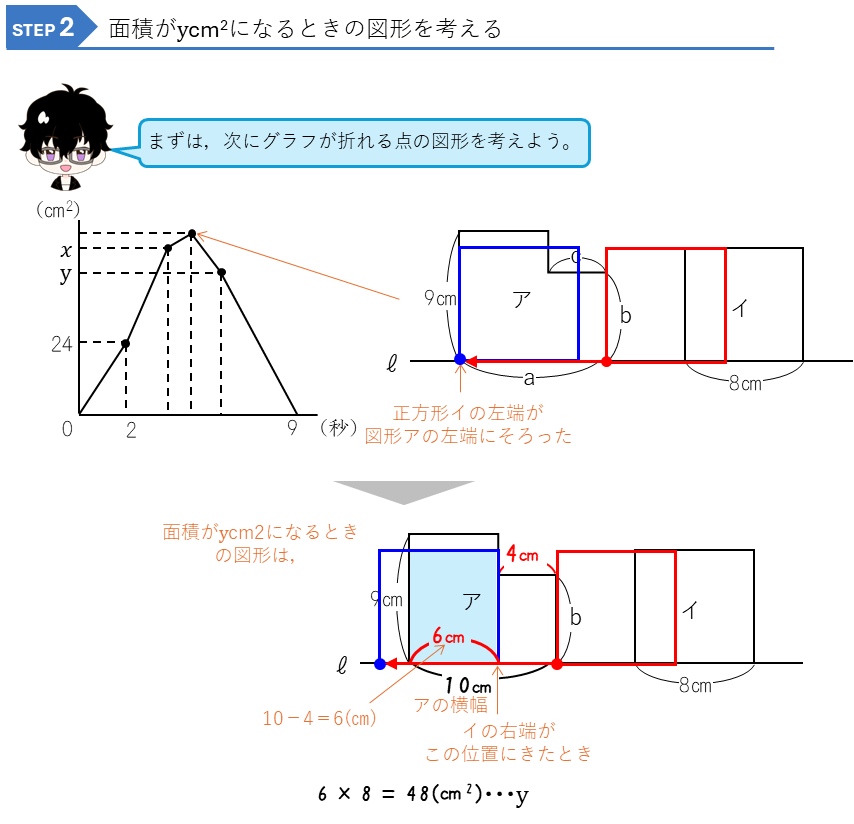
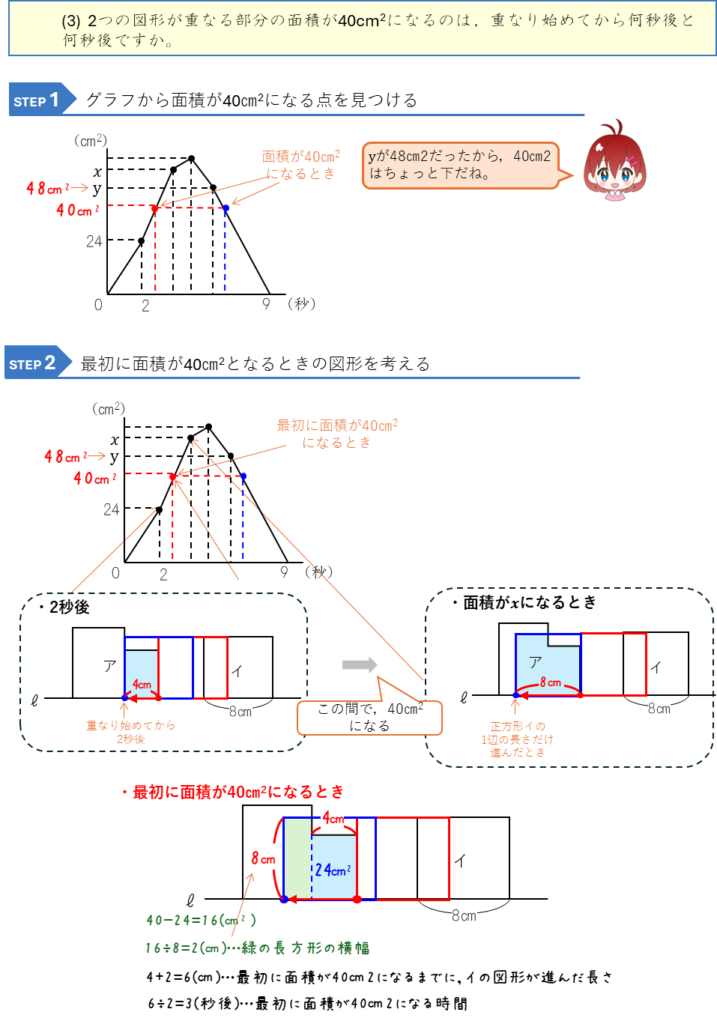
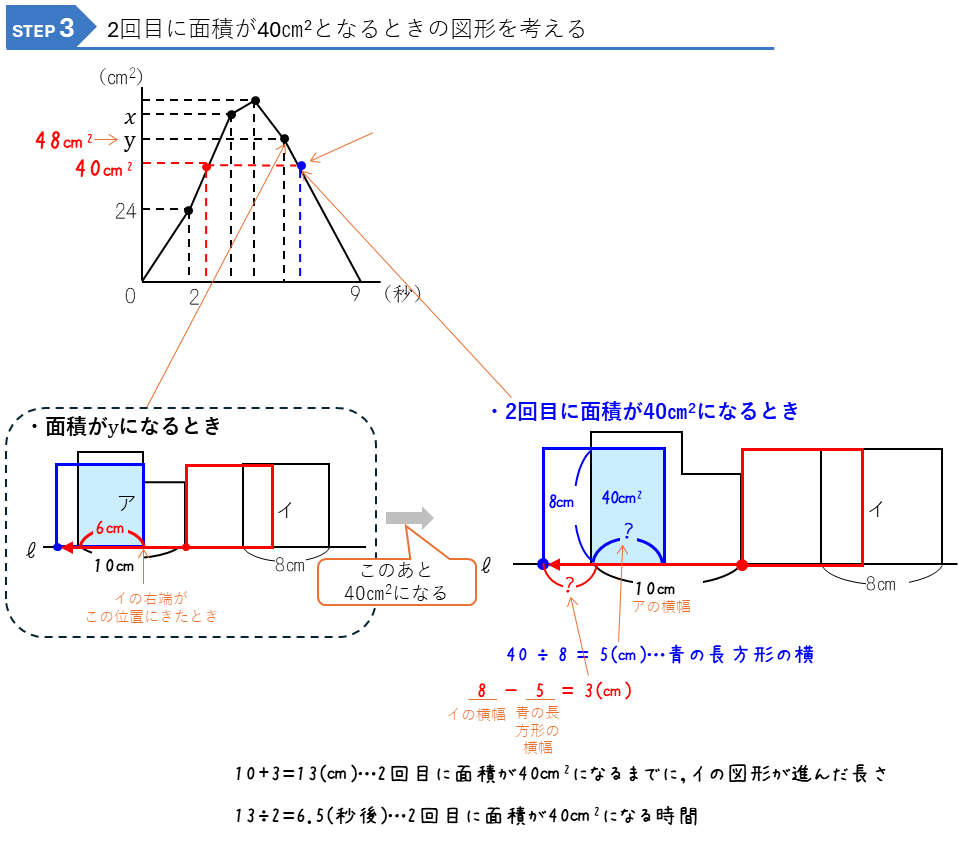
図形の平行移動とグラフ
コメント
分かりやすい!もしよければ、大阪大谷中学校の過去問題集を何年でも良いのでほしいです。後、解説してほしいです。
コメントありがとうございます。 横浜にいるもので、お問い合わせの大坂大谷中学校については詳しくありませんが、問題集は市販されていますし、四谷大塚の「過去問データベース(登録が必要)」からも入手できますよ。
試しに四谷大塚のデータベースから2024年の問題を入手して解いてみました。ひねった問題などなくて基本レベルの問題でした。大問4⃣の仕事算と6⃣の円周上の旅人算の問題は、ともに逆比の考え方を使うものでした。大問で同じ解き方を使う問題が出てきていることが少し気になりました(分かっていないと両方失点する可能性あり)。