
「線分図」について解説しましたが、今回は、これもいろいろな問題に使われる「面積図」について解説していきます。
速さ、割合や、特殊算など、かけ算(積)の形の公式は10種類くらいあります。覚えるだけでも大変ですね。それを使いこなすとなると、さらに難易度が上がります。長方形の面積は、たて×横=面積という積になっているので、かけ算の形の公式を、長方形をかいて考えていくと、計算に具体的なイメージを持つことができます。この長方形の図が面積図です。
面積図の解説の、第1回では、かけ算とわり算を表す面積図の基本から、積の形の公式をまとめてます。面積=たて×横という積の形を覚えておけば、面積の考え方で他の公式を作ることができることを理解しましょう。
第2回以降は、面積図を使った特殊算などの問題を解説します。第2回では、つるかめ算とそれを使った特殊算などの問題を、第3回では、濃度算(食塩水)、平均算を、第4回では、逆比の問題を面積図で解いていきます。
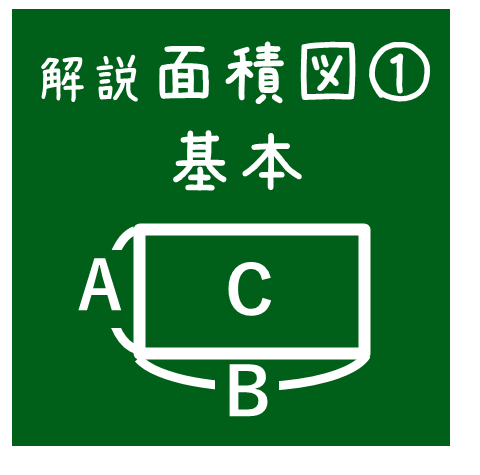
面積図の基本
長方形の面積は,「たて×横」で計算できます。面積図は,長方形をつかって,かけ算やわり算を表し,図形としてかけ算やわり算の式を具体的なイメージにしたものです。

具体的な例で、面積図をかいてみましょう。

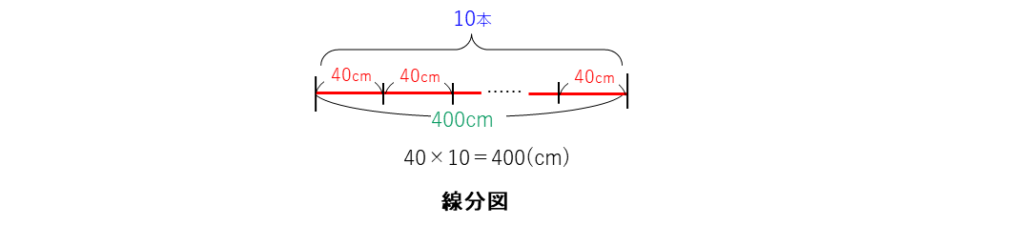
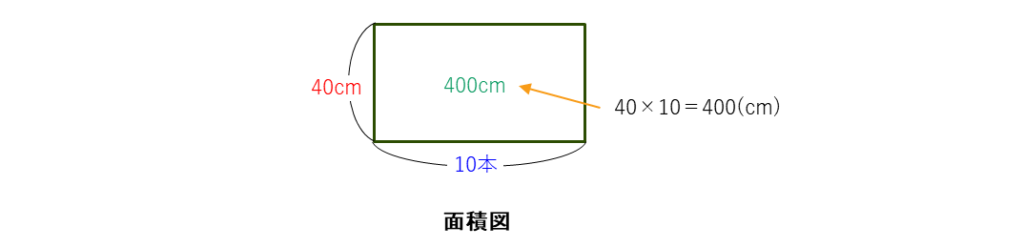
この問題は、線分図を使って図にすることができます。線分図の解説で説明した通り、これで問題を解く場合もありますが、面積図で表すこともでき、積の形の式を使う問題では面積図で考える場合も多いです。
「かけ算」と「わり算」と面積図
「かけ算」の面積図
かけ算は、
「ぜんぶの数」 = 「1つあたりの数」×「いくつ分」
を意味しています。

この問題では、
1つあたりの数=2個
いくつ分=3人分
になるので、ぜんぶの数は、

で計算できます。これを面積図で表すと、
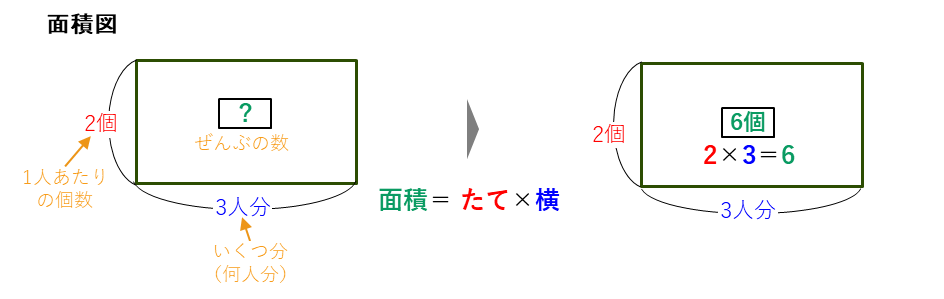
たてが1つ(1人)あたりの個数の2個、よこが3人分、長方形の面積が求める全部の数となります。面積=たて×横から、リンゴぜんぶの数を求めることができます。
「わり算」の面積図
これは、とても大切なことですが、わり算には2種類があります。「1つあたりの数」を求めるわり算と,「いくつ分」を求めるわり算です。それぞれについて、面積図をかいてみましょう。
① 「1つあたりの数」を求めるわり算
このわり算は、「ぜんぶの数」を,同じ数ずつ「いくつ分」かに分けて「1つあたりの数」を求めるものです。式にかくと、次のようになります。
「1つあたりの数」 =「ぜんぶの数」÷「いくつ分」
例題で考えてみましょう。

この問題では、
ぜんぶの数=6個
いくつ分=3人分
になるので、1つ(1人)あたりの数は、

で計算できます。これを面積図で表すと、
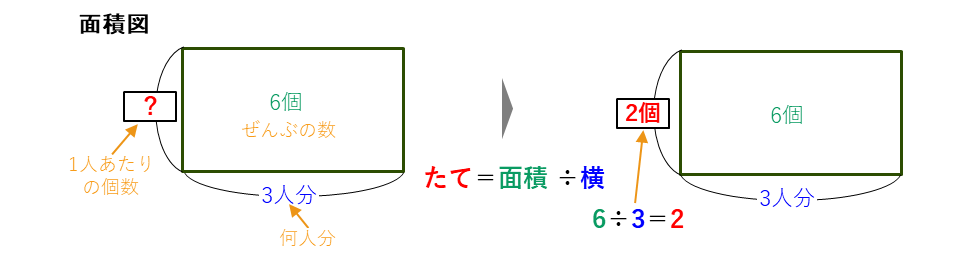
長方形の面積が全部の数6個で、よこが3人分、たてが求めたい1人あたりのリンゴの数となります。長方形のたて=面積÷横から、1人あたりのリンゴの数を求めることができます。
② 「いくつ分」を求めるわり算
このわり算は、「ぜんぶの数」の中に,「1つあたりの数」が「いくつ分」あるかを求めるものです。式にかくと、次のようになります。
「いくつ分」 =「ぜんぶの数」÷「1つあたりの数」
例題で考えてみましょう。

この問題では、
ぜんぶの数=6個
1人あたりの数=2個
になるので、いくつ分は、

で計算できます。これを面積図で表すと、
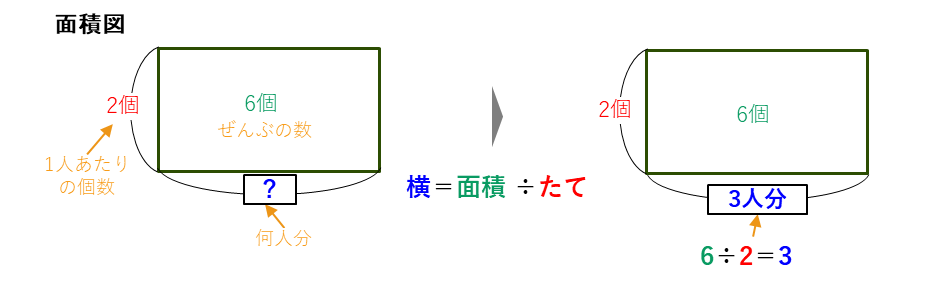
今度は、面積図の長方形のよこを求めることになります。長方形の面積が全部の数6個で、たてが求めたい1人あたりのリンゴの数2個です。長方形の横=面積÷たてから、いくつ分(何人分)を求めることができます。
主な積の形の公式と面積図
速さの公式など,かけ算を使った公式は10種類ほどあります。それぞれについて3つの公式がありますが,積の形の式だけ覚えておけば、あとは、面積図で考えることができます。これで、覚える量が大幅に少なくすることできます。覚えたはずの公式が正しいか確信が持てない場合には、面積図をかいて確認することもできます。
速さの公式の例
速さの公式は、次の3つです。
速さ=きょり(道のり)÷時間…速さの定義
きょり(道のり)=速さ×時間
時間=きょり(道のり)÷速さ
この3つを覚えて使いこなさないといけないのですが、「きょり(道のり)=速さ×時間」の式だけ覚えていれば大丈夫です。面積図をかけば、面積の式「たて=面積÷横」、「横=面積÷たて」から、残りの2つの式の計算ができます。
きょりを求める式から、次の面積図がかけます。
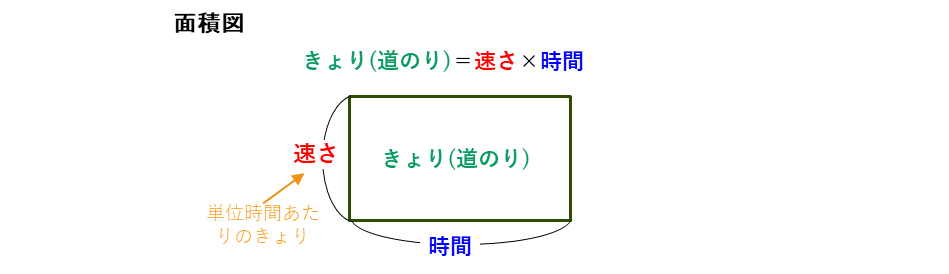
速さを求める場合は、面積図の長方形のたてにあたるので、「たて=面積÷横」から、
速さ=きょり(道のり)÷時間
を計算すればよいことが分かります。
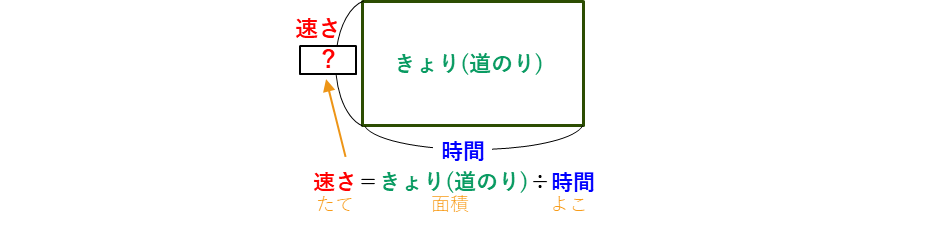
また、時間を求める場合は、面積図の長方形の横にあたるので、「横=面積÷たて」から、
時間=きょり(道のり)÷速さ
を計算すればよいことが分かります。

以上、文章と式で説明してきましたが、この説明より面積図をみれば簡単に計算方法が考えつくと思います。
主な積の形の公式のまとめ
10種類の積の形の公式を表にまとめます。

それぞれの公式の面積図をカード形式にまとめておきます。
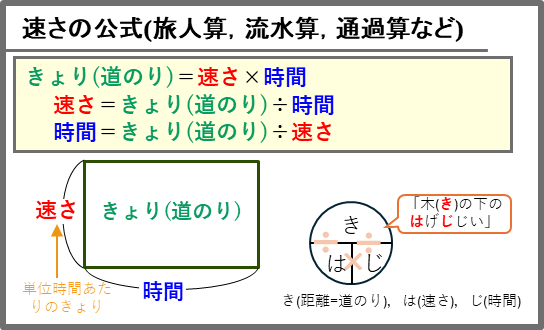
速さの公式(旅人算,流水算,通過算など)
右下の”きはじ”の図からも計算できますが、面積図でも同様に計算できます。
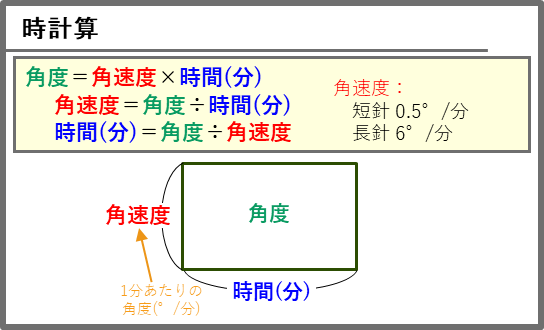
時計算
仕事算

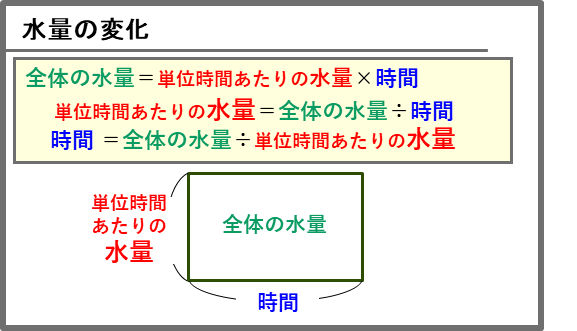
水量の変化
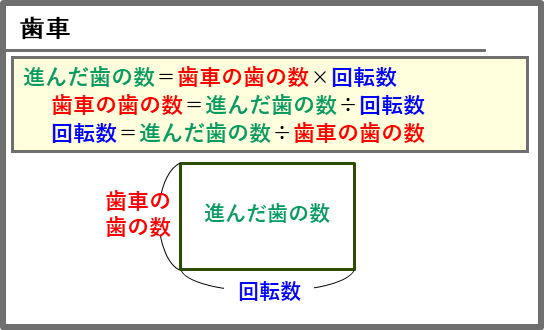
歯車
歩幅と歩数

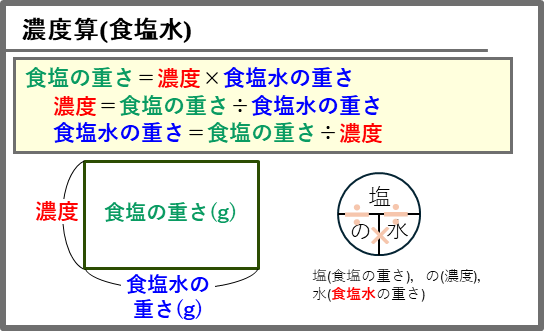
濃度算(食塩水)
速さの公式と同じように、右下の「塩の水」の図で計算できますが、面積図も覚えましょう。
平均算

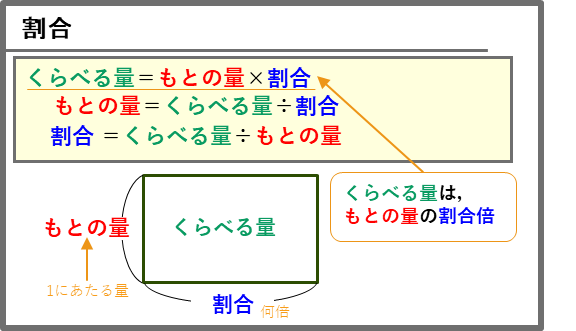
割合
例えば、「100の0.4倍は?」という問題は、そのまま、「100×0.4=」にすることができるので、
くらべる量=もとの量×割合
の式は出てくると思います。
もとの量=くらべる量÷割合
が一番難しい式ですが、面積図で考えれば計算できます。
水の体積

(印刷用に1枚にまとめたものをリンクしておきます。)

面積図の基本と積の形の公式の面積図をまとめました。それぞれの公式の3つの形をしっかり使いこなせるのであれば、面積図で考える必要はないのですが、積の形の公式は今回取り上げたものでも10種類と数が多いので、必要に応じて面積図を使うとよいです。
さて、第2回以降は、面積図を使った特殊算などの問題を解説します。第2回では、つるかめ算とそれを使った特殊算などの問題で、複数の長方形の面積を使って問題を解いていきます。
コメント
とってもわかりやすくて勉強になりました。塾でも遅れていたのですが、頑張れそうな気がします。
コメントありがとうございます! これからも分かりやすい解説を書いていきますので、よろしくお願いします。
中学受験 算数:面積図で解こう!①面積図を勉強しています。
年取った私にもとにかく先生の説明は分かり易い。
先生ありがとうございます。
コメントどうもありがとうございます。励みになります♪♪
これからも分かりやすい解説を載せていきます。どうぞよろしくお願いします。