
この単元では、2人がすれちがったり、追いこしたりするまでの時間を求めたりする「旅人算」を勉強します。2人が反対の方向に進む場合は2人の速さの和で近づいて、2人が同じ方向の場合は2人の速さの差で追いかけることになります。図をかいて、2人のはじめのきょりと2人の速さ、そして方向をみつけて問題をといていきましょう。旅人算の問題も速さのグラフとしてかくことができます。グラフに2人の線があって、その2本の線が交わる点が2人がすれちがったり、追いこしたところを示しています。グラフの読み方をしっかり理解してといていきましょう。
(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説
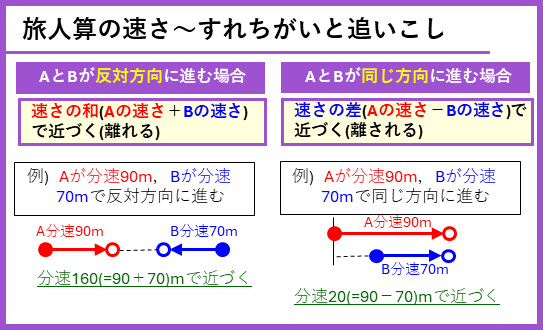
今回は、「旅人算」という、2人がすれちがったり、追いこしたりするまでの時間を求める問題を勉強します。旅人算は、「2人の方向」に気をつけて「2人のきょりの和や差」と「2人が近づく速さ」を考えることがポイントです。
2人が近づく速さ
- 2人が同じ方向に進む場合: 2人の「速さの差」で近づく
- 2人が反対の方向に進む場合: 2人の「速さの和」で近づく
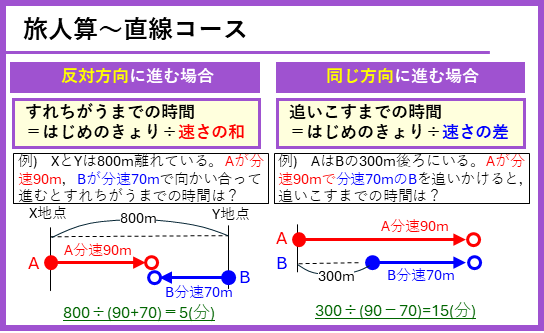
直線コース ー 2人が出会う(すれちがう、追いこす)までの時間
2人が、出会う(すれちがう、追いこす)までの時間は、
- 2人が反対の方向に進む場合: すれちがうまでの時間=はじめのきょり÷速さの和
- 2人が同じ方向に進む場合: 追いこすまでの時間=はじめのきょり÷速さの差
となるので、2人の進む方向に注意して、2人のきょりと2人の速さがわかれば、問題を解くことができます。
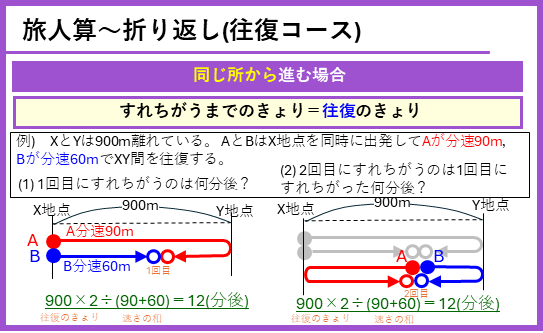
往復コース ー 同じところから進む場合
旅人算には、2人が2つの地点を往復して、繰り返してすれちがう問題もあります。同じところから進む場合は、2人で往復のきょりを進んだときにすれちがうことになります。
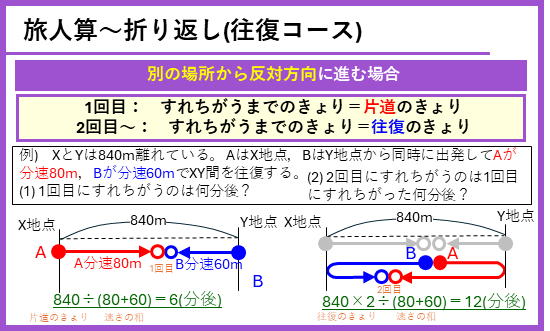
往復コース ー 別の場所から反対方向に進む場合
別の場所から反対方向に進む場合には、1回目だけは片道のきょりで、2回目以降は上の場合と同様に、同じ場所からスタートするので2人で往復のきょりを進んだときにすれちがうことになります。丸暗記するのではなくて、はじめは自分で図をかいて理解しておきましょう。
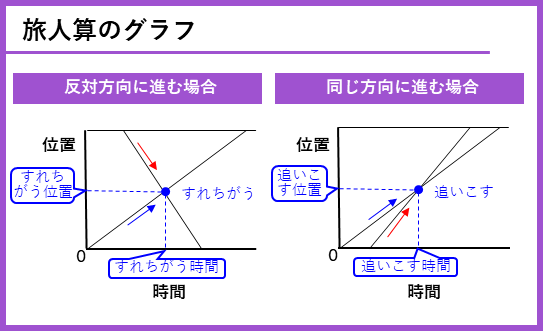
旅人算とグラフ
旅人算の問題も速さのグラフとしてかくことができます。速さのグラフ(ダイヤグラム)と同じように、たて軸がきょり(位置)で横軸が時間になります。グラフに2人の線があって、その2本の線が交わる点が2人がすれちがったり、追いこしたところになります。
練習問題
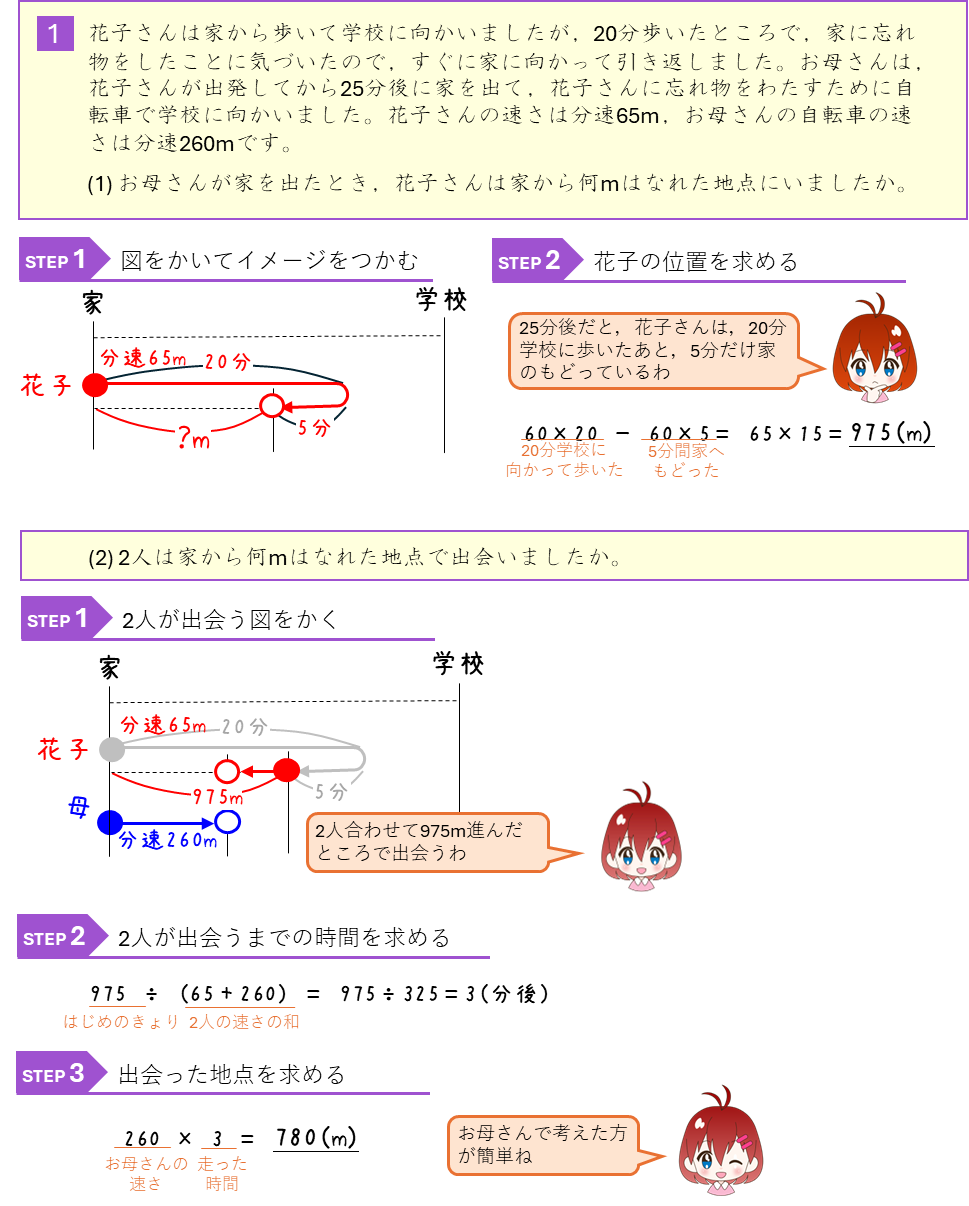
旅人算ー2人が出会う
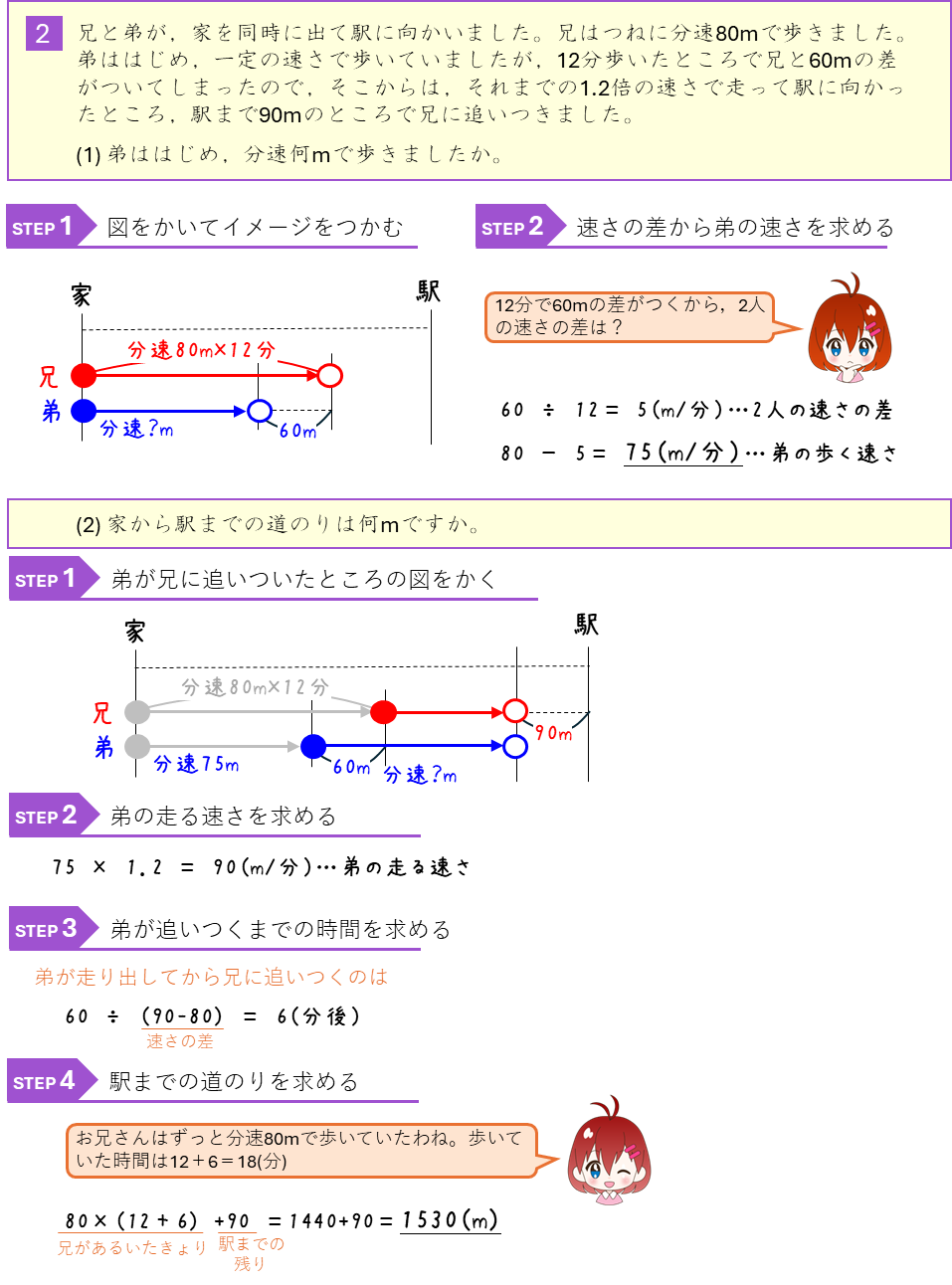
旅人算ー兄に追いつく
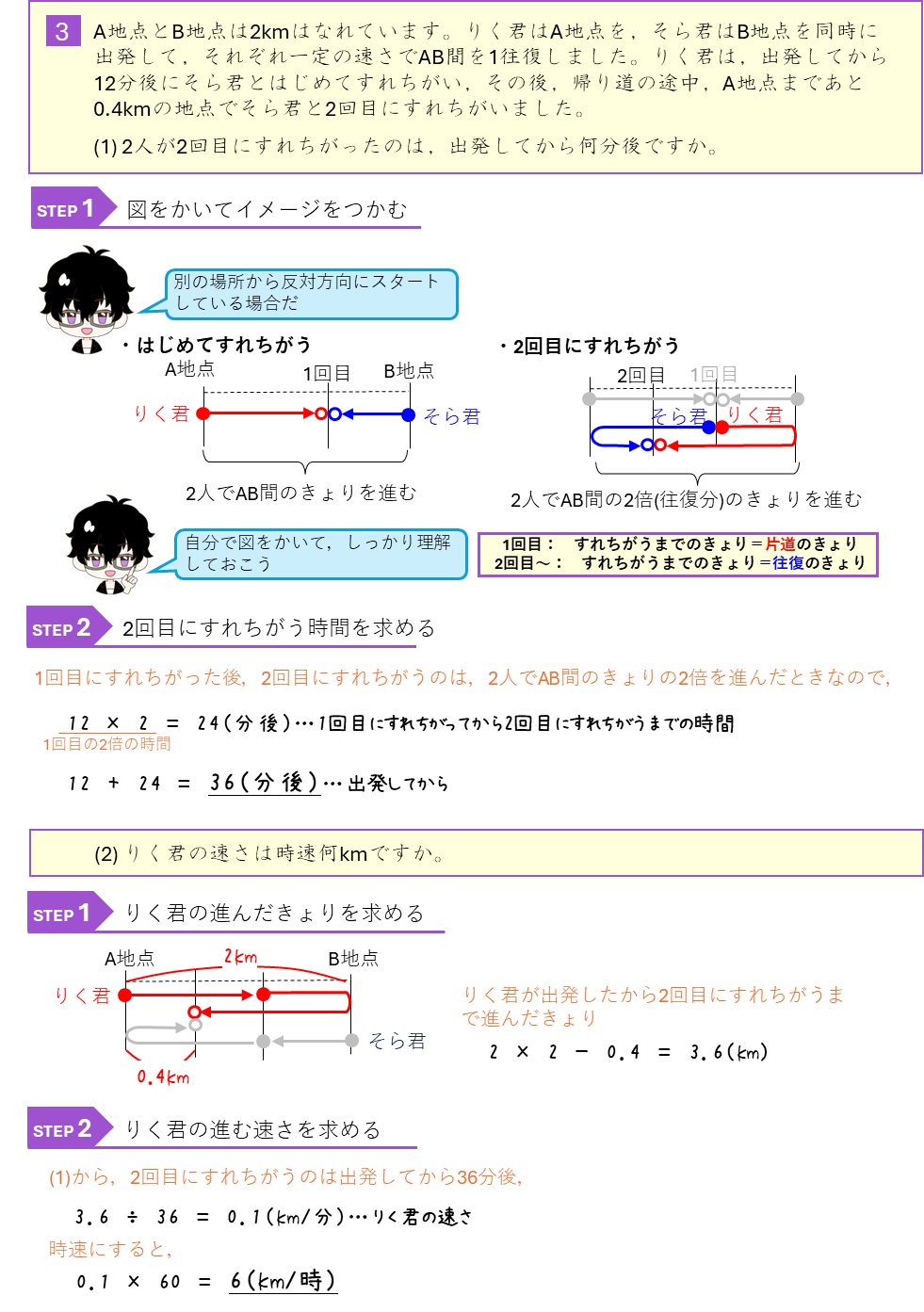
旅人算ー折り返し
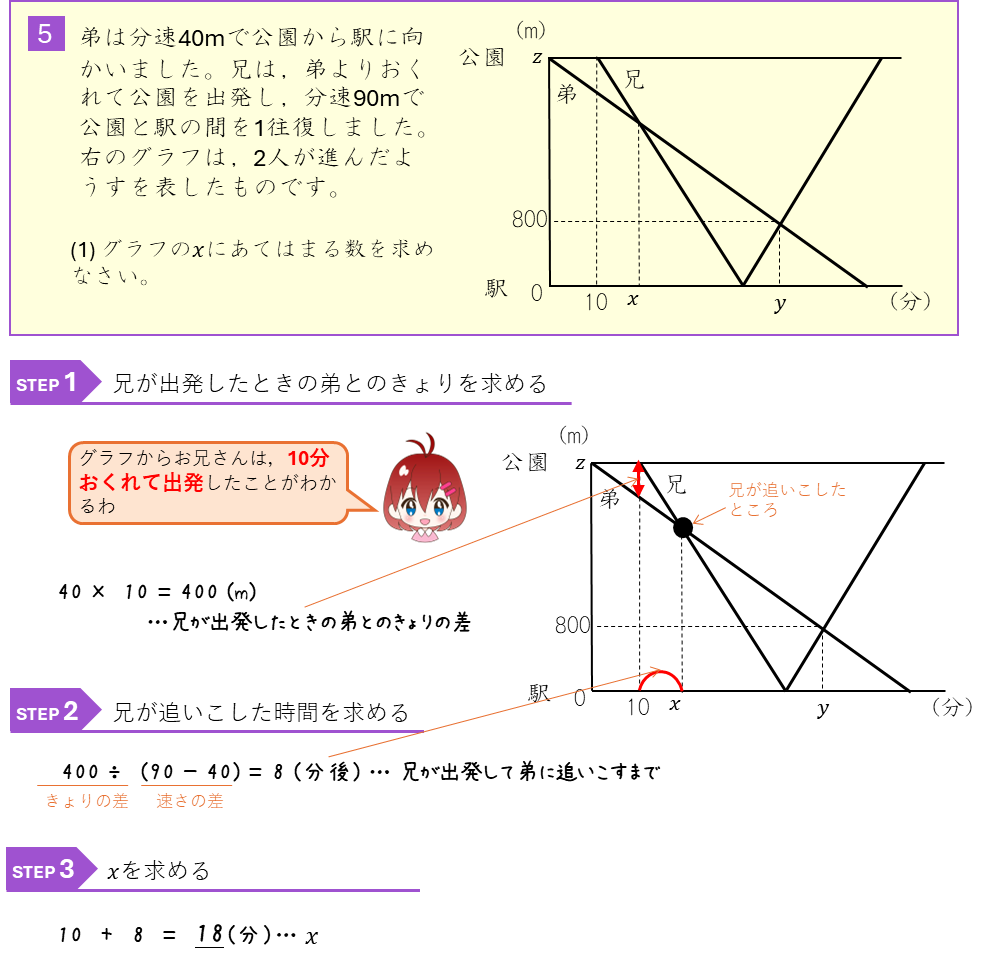
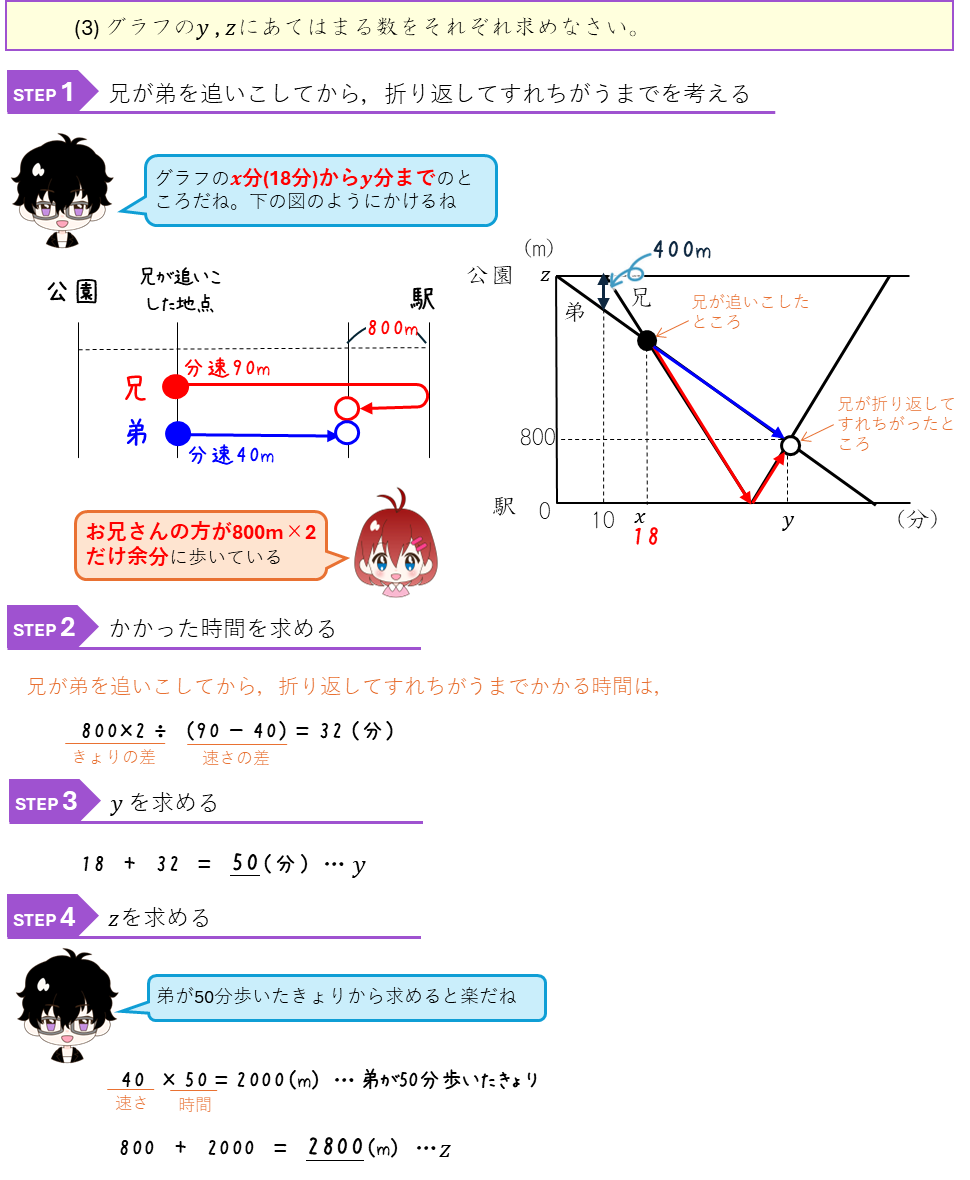
旅人算とグラフ
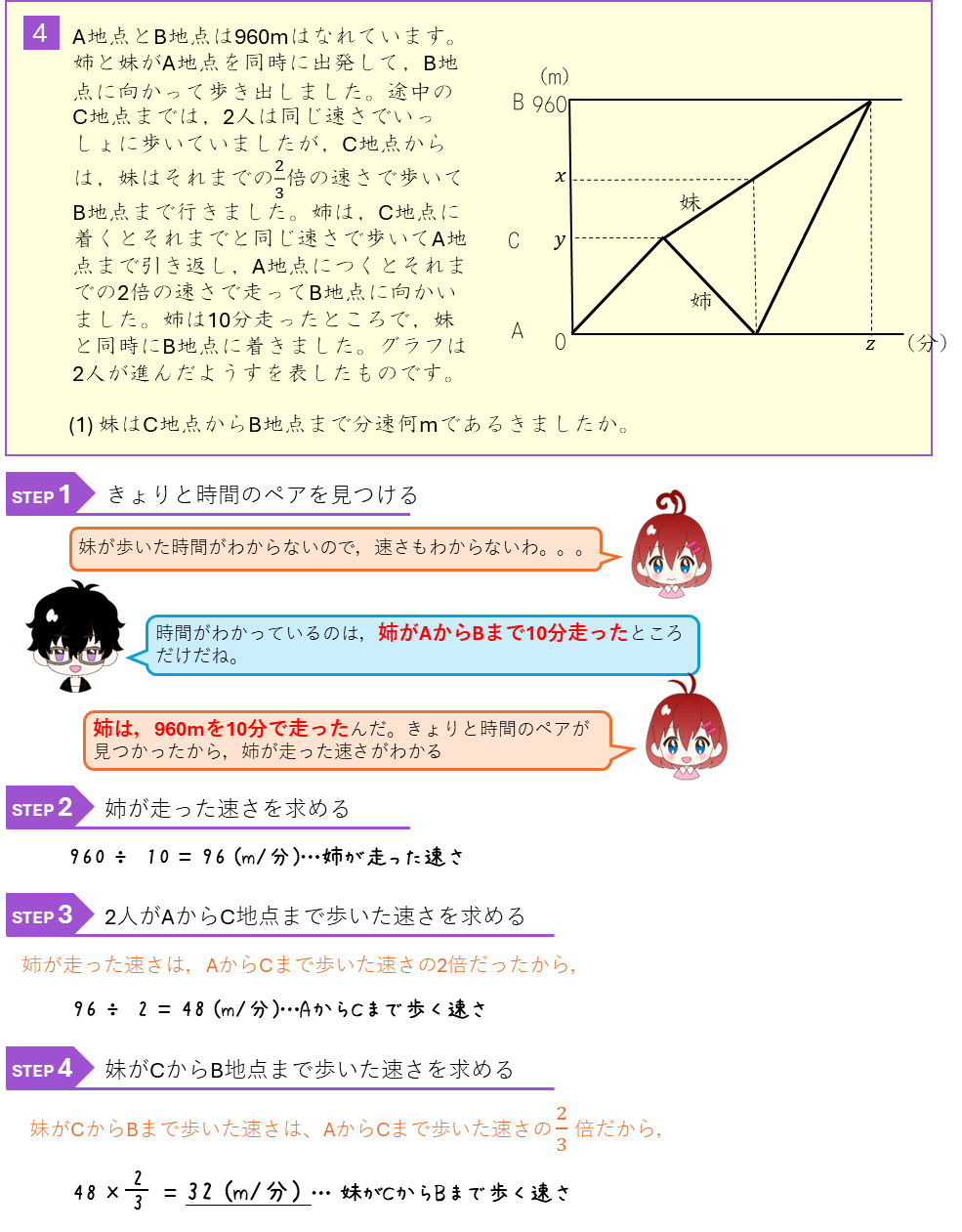
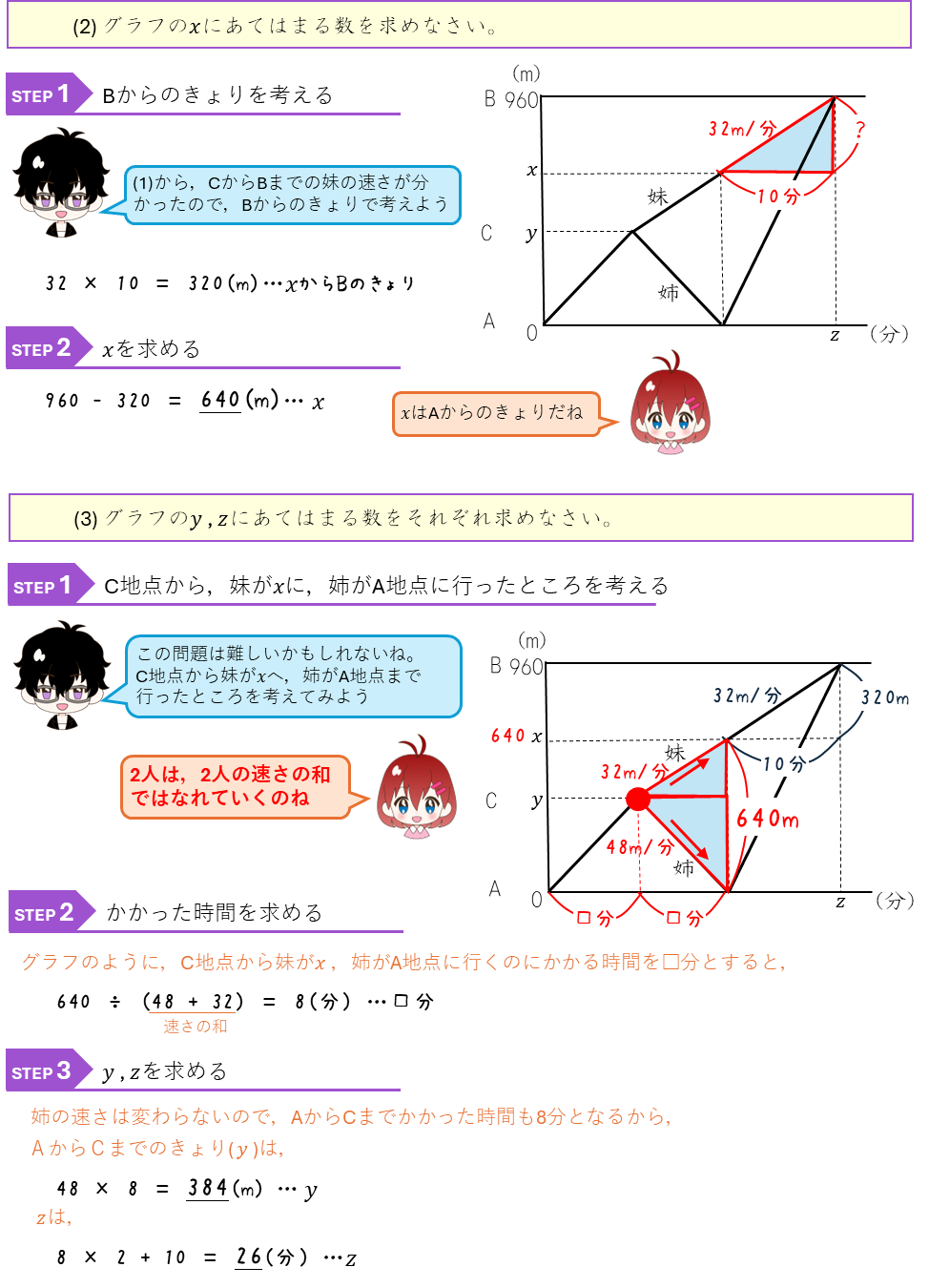
旅人算とグラフ

コメント