
”図をかいて解こう!”の3番目の図形の、”おだんご図”について説明します。おだんご図という言い方は一般的ではなくて、単に”図表”と言われているのですが、この図はいろいろな特殊算に共通に使う図ですので、ここでは”おだんご図”と名前をつけました。
かけ算やわり算の文章題や、特殊算の差集め算(過不足算)、つるかめ算、弁償算とりちがえ算で具体的なイメージがわいて問題が解きやすくなります。ぜひ、使いこなせるようにしましょう。
おだんご図とは、
次の例題を考えてみます。

線分図や面積図でも、図で表すことができますが、次のような図で表すこともできます。
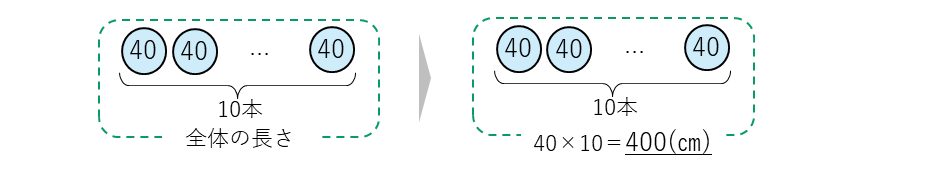
1本の量を〇数字でかいて、それを10本ならべた図です(実際には10個もかけないので、…でつなげてイメージします)。丸いおだんごをならべているようなので、これを「おだんご図」と名づけました。問題の答えは、1本あたりの長さが40㎝で、全体の長さはその10本分になるので次のかけ算、
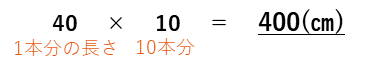
で求めることができます。
おだんご図の基本ー「かけ算」と「わり算」のおだんご図
まずは、基本のかけ算とわり算のおだんご図です。
「かけ算」のおだんご図
面積図の基本で説明した通り、かけ算は、
「ぜんぶの数」 = 「1つあたりの数」×「いくつ分」
を意味しています。かけ算のおだんご図では、
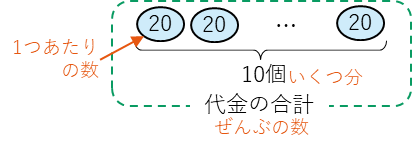
のように表します。求めるぜんぶの数(この場合は、代金の合計)は、
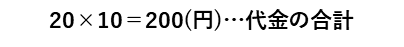
で求められます。
「わり算」のおだんご図
「1つあたりの数」を求めるわり算と,「いくつ分」を求めるわり算の2つのわり算について、それぞれについておだんご図で表してみます。
① 「1つあたりの数」を求めるわり算
最初のわり算は、「ぜんぶの数」を,同じ数ずつ「いくつ分」かに分けて「1つあたりの数」を求めるものです。

ぜんぶの数が代金の合計の400円で、いくつ分がおだんごの10個で、1つあたりの数、つまり、おだんご1個の値だんを求める問題です。これをおだんごでかくと、
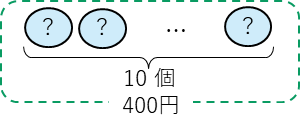
となります。ここからおだんご1個の値だんが、わり算の式、
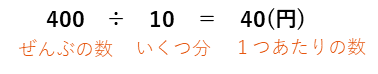
で求られることがイメージできましたか?
② 「いくつ分」を求めるわり算
次のわり算の例は、「ぜんぶの数」の中に,「1つあたりの数」が「いくつ分」あるかを求めるものです。

ぜんぶの数が代金の合計の300円で、1つあたりの数がおだんご1個の値だんの15円で、いくつ分(おだんごが何個か)を求める問題です。これをおだんごでかくと、
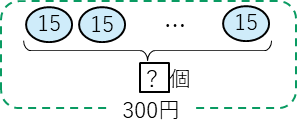
となります。ここからおだんごの個数が、わり算の式、
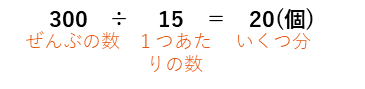
で求られます。
簡単なかけ算、わり算の例でしたので、図をかくまでもなく式が頭に浮かんでしまうかもしれませんが、おだんご図での表し方を理解して、パパっとかけるようになりましょう。
次回は、このおだんご図を使って、特殊算の差集め算(過不足算)、つるかめ算、弁償算、とりちがえ算を解いていきます。

コメント