今回は、濃さの問題（濃度算）を比を使って解いていきます。食塩水を混ぜ合わせる問題では、面積図を使って解く方法を勉強しました。今回は「てんびん図」を使う解法も学びます。てんびん図は、覚えやすく、かくのも楽なので、ぜひ使いこなせるようにしましょう。
（四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
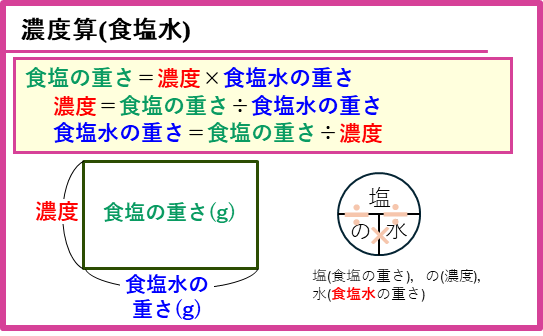
食塩水の濃さ（濃度算）の公式
食塩水の濃さ（濃度算）の公式をまとめます。この3つの式のうち、積の形の式
食塩の重さ=濃度×食塩水の重さ
から面積図をかけば、残りの式を作ることができます。
濃度算の面積図による解法
復習で、濃度算の面積図の解法をまとめます。2種類の食塩水をまぜる問題では、次の3ステップで解いていきます。
具体的な例題を考えます。
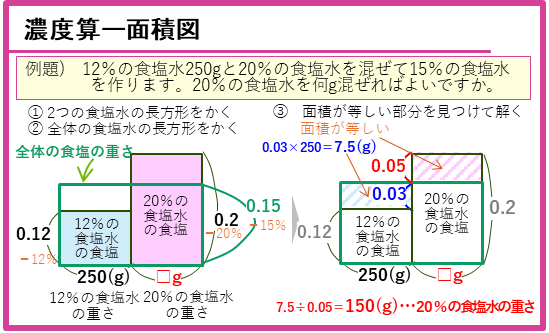
2種類の食塩水と、混ぜた後の全体の食塩水の3つの長方形をかいて、面積（食塩の重さ）の等しい部分を見つけて解いていきます。
濃度算のてんびん図による解法
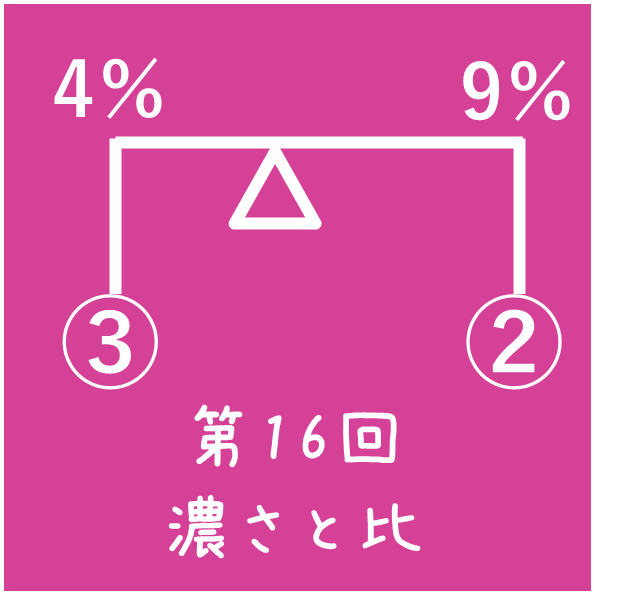
濃度算を比を使って解くときは、てんびん図がより簡単で分かりやすい解法になります。
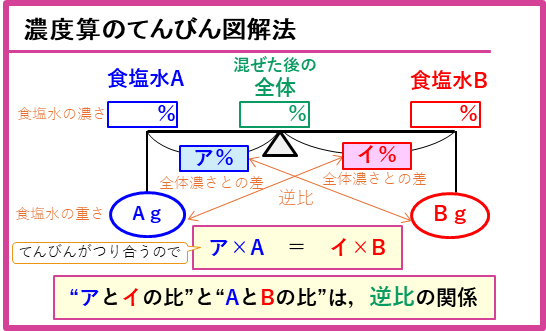
てんびん図は、上の例題の面積が等しい部分をてんびんの図として表したものです。
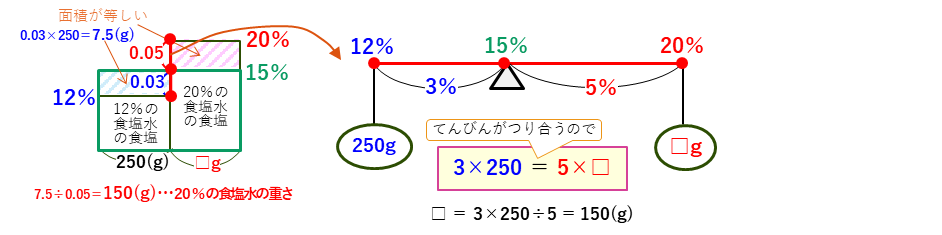
ここで、「食塩水の全体の濃さとの差」が「てんびんの支点からのきょり」になります。また、全体の濃さとの差や食塩水の重さは、そのままの値（％やg）ではなくて、比として解くことができます。このとき、全体の濃さとの差と食塩水の重さの積は一定なので、
全体の濃さとの差の比と食塩水の重さの比は、逆比の関係
になります。逆比を使うと、上の例題は次のようなてんびん図で解くことができます。
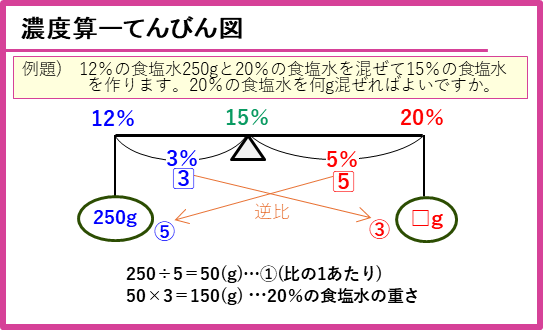
てんびん図の解法をまとめておきます。
濃度算では、てんびん図は強力な解法になりますので、今回の単元の中で理解して、使いこなせるようにしましょう。
練習問題
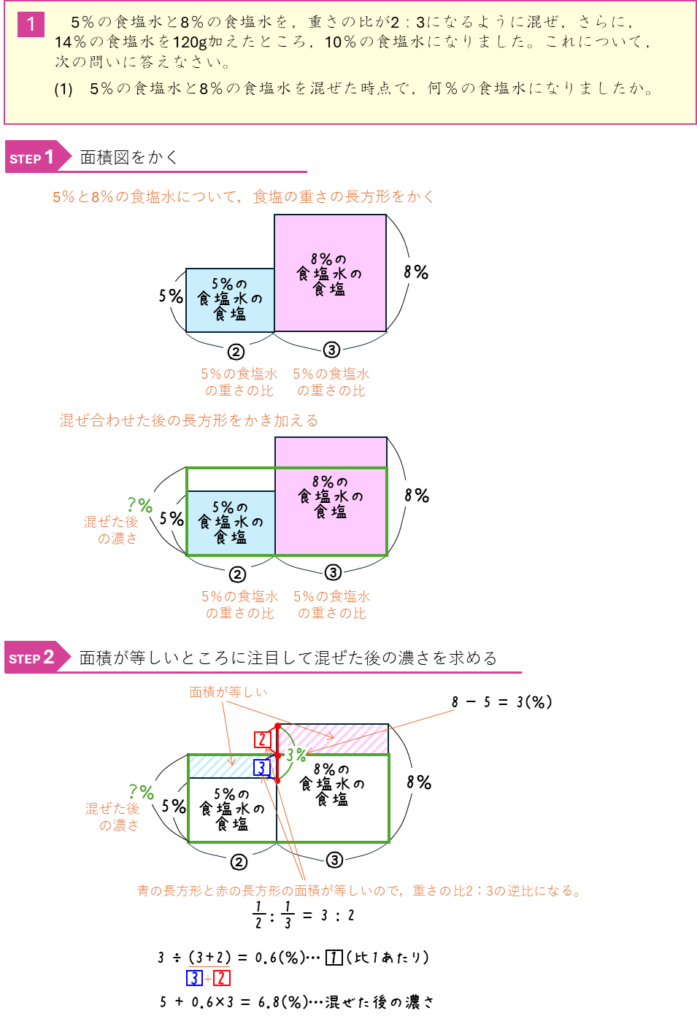
食塩水の混合と比ー重さの比から解く
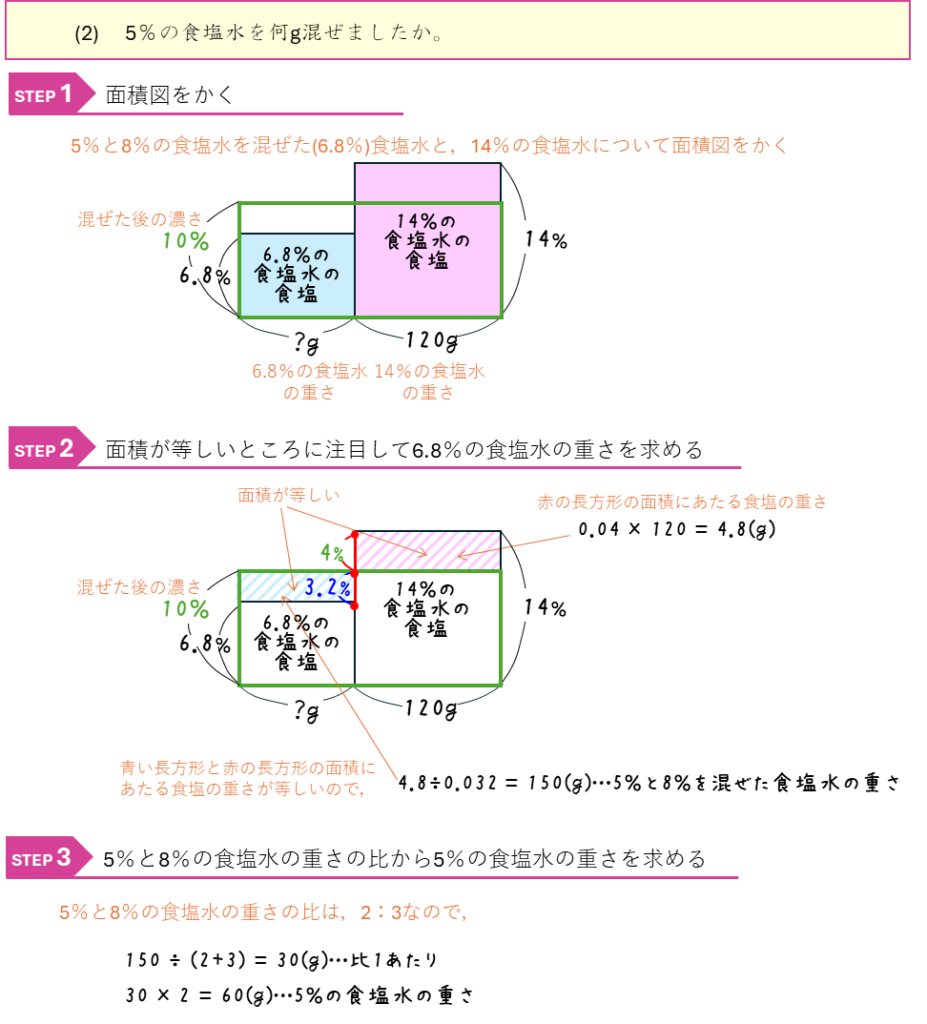
食塩水の混合と比ー濃さの比から解く
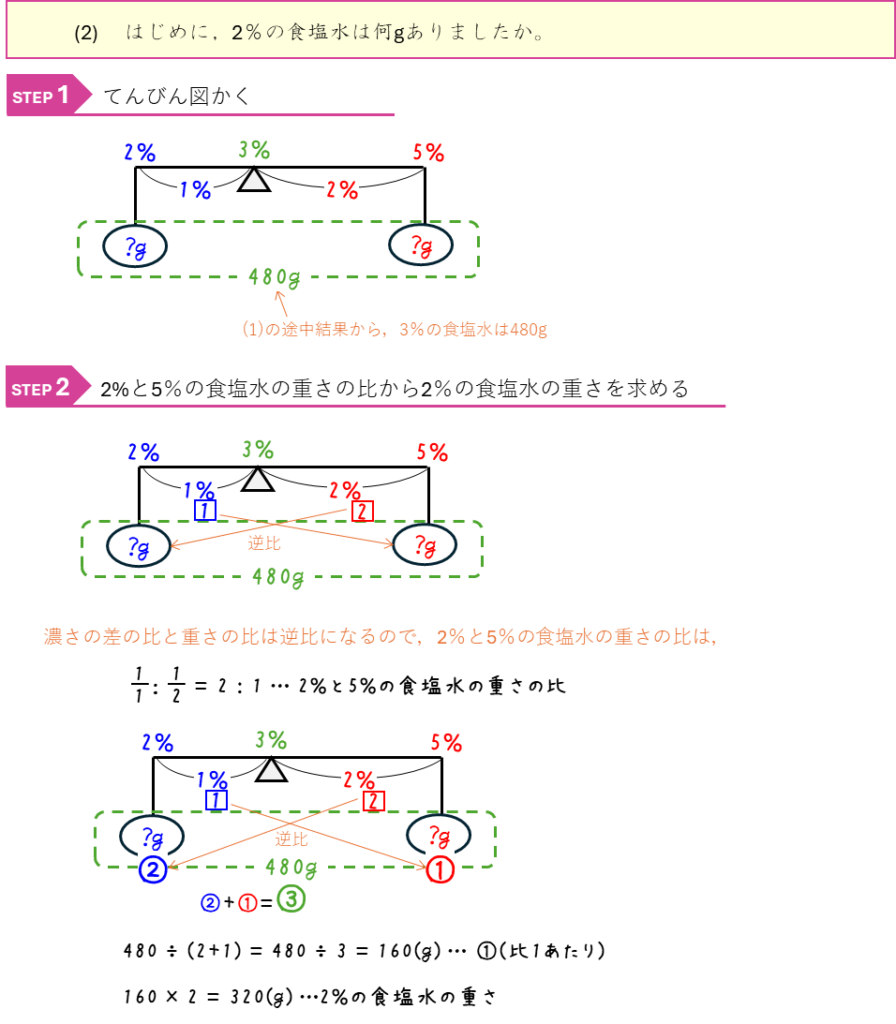
食塩水の混合と比ー食塩水の重さの比を求める
食塩水の混合のやりとり①
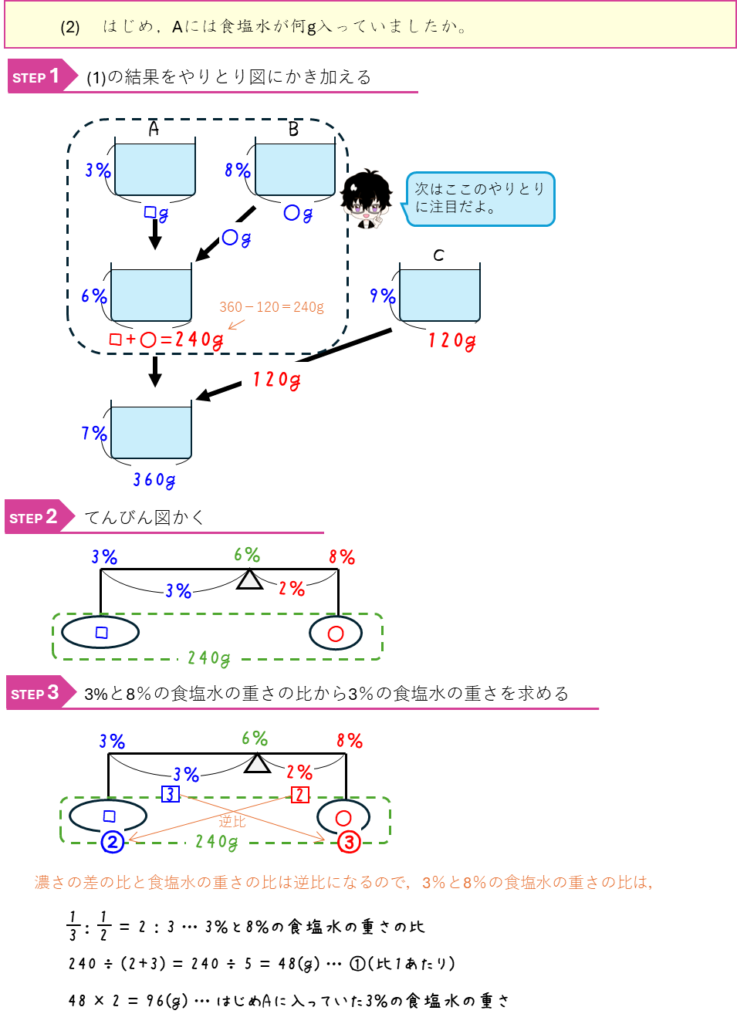
食塩水の混合のやりとり②
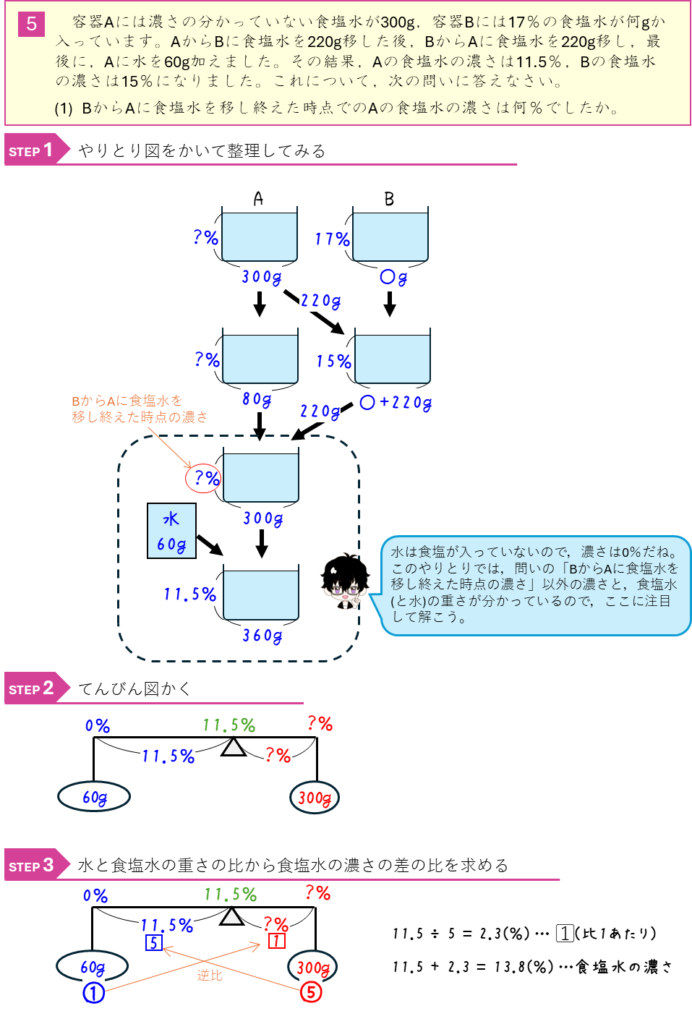
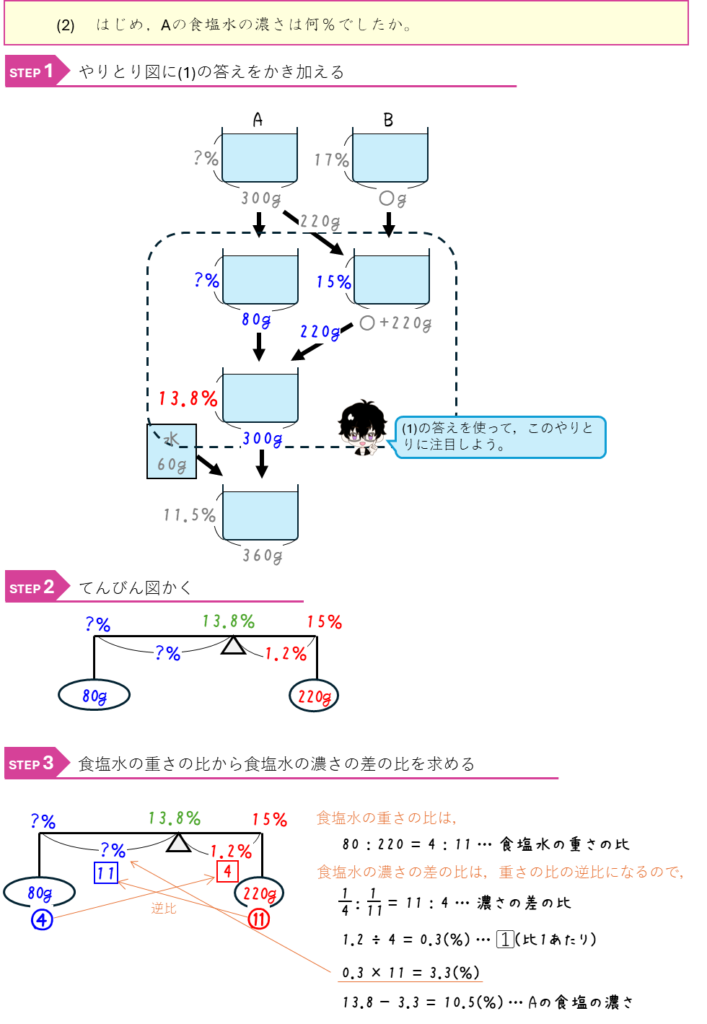
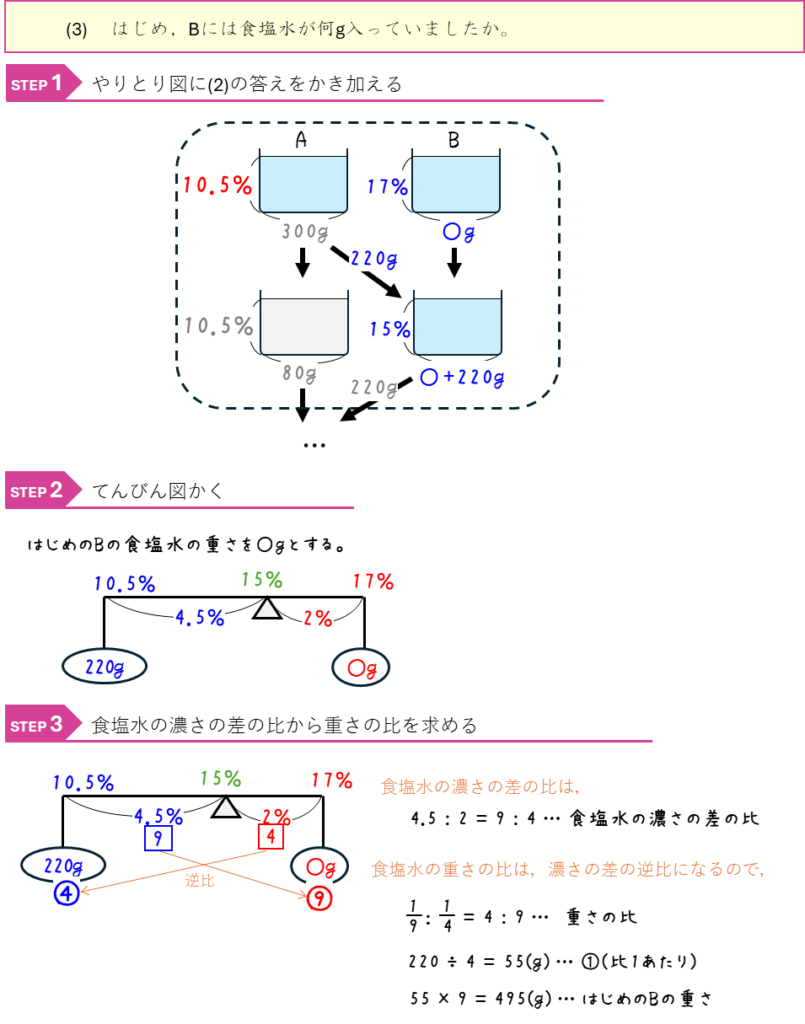
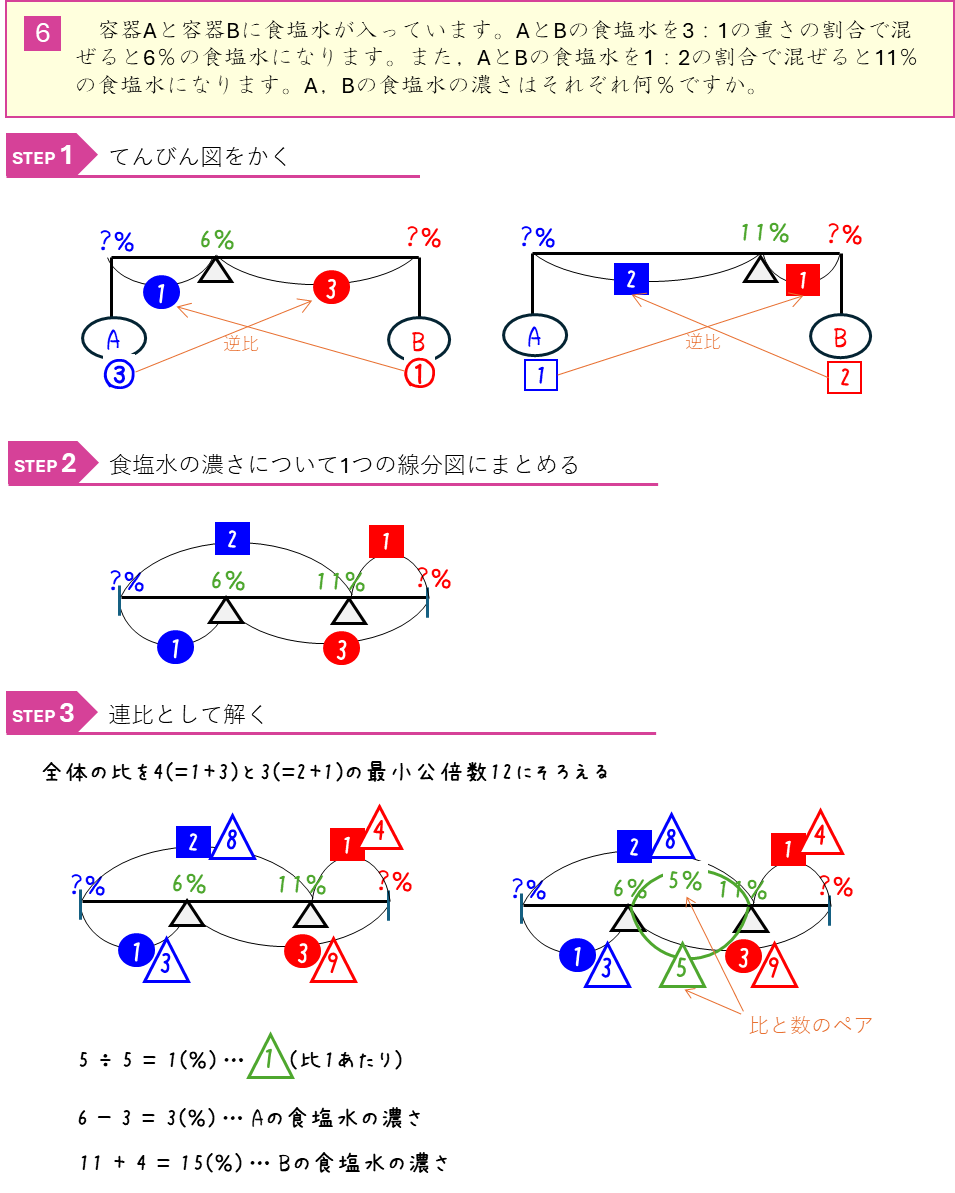
食塩水の混合と比ー連比として解く
コメント