
「面積図で解こう!」の第4回目、今回が最終回になります。「逆比」を使う問題を面積図で考えていきます。
いろいろな問題で逆比が出てきますが、苦手にしている人が多いのではないでしょうか? 逆比を使う問題では分からない数が多いので,それが難しさを高くしています。そこで逆比を面積図をかいて考えてみましょう。これによって、よりイメージを持って解くことができるようになります。
逆比を使う問題の特徴と面積図を使った解法
逆比を使う問題の特徴
逆比を使う問題を見てみましょう。

これらの問題には、次の共通点があります。
積の式になる
まず最初の特徴は、積の式で表される問題になっています。

例題1⃣は速さ、例題2⃣は仕事量の積の式になっていますね。
分かっている数が少ない
逆比を使う問題は、実際に分かっている数が少ないです。

たとえば、速さの問題では、速さ、時間、道のり(きょり)の3つの量が出てきます。普通の問題では2つの量が分かって、速さの公式を使って残り1つを計算しますが、逆比を使う問題では、1つの量しかその数が分かっていないのです。1つだけでどうやって解くのか?と悩んでしまうところです。
2つ以上の場合がある
分かっている数が少ないのですが、かわりに2つ以上の場合が出てきます。上の例題では、

となっています。
積が一定(でも、いくつか分からない)
最後の特徴はとても重要です。問題に出てきた2つ以上の場合で積が一定となっています。

でも、積の値がいくつかは問題文には書いていないので分かりません。
逆比の面積図3ステップ解法
上の3つの特徴が分かれば、逆比として比を求めて解いていけばよいのですが、今回は面積図をかいて考えてみます。逆比を使う問題の面積図による解法は、次の3つのステップになります。
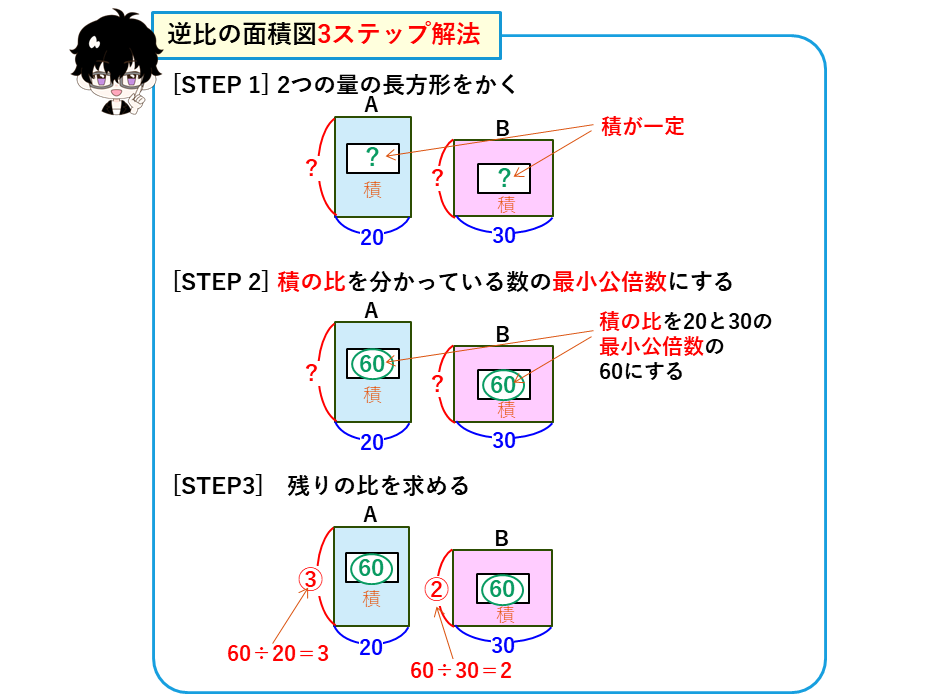
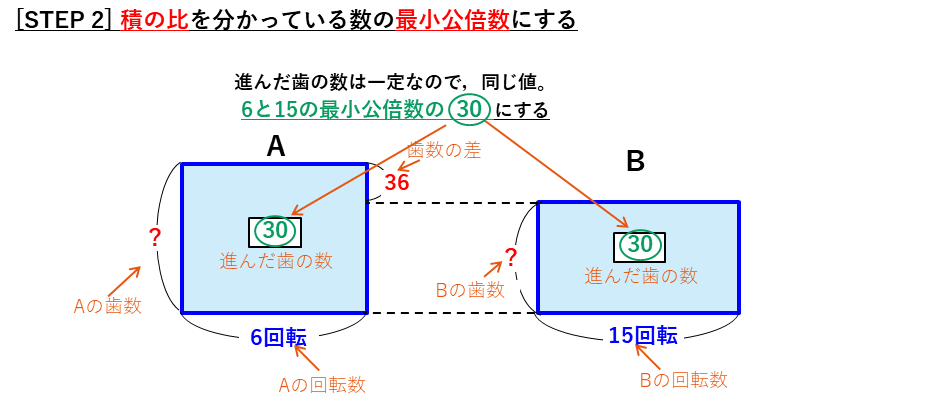
特に、重要なのはSTEP 2の、
積の比を分かっている数の最小公倍数にする
というところです。まだ分からない積に、適当な比をおくということにとまどうかもしれませんが、2番目のステップでこれを行います。実のところ、積の比をどのような数にしても正解にたどり着くことができるのですが、最小公倍数にすることで、STEP3の残りの比がわり切れる最も小さい数になるので、その後の計算が楽になります。
それでは,逆比を使う例題を実際に解いていきましょう。
逆比を使う問題を面積図で解いてみよう
速さの平均

速さの平均を求める問題は、逆比の特徴を持っています。

逆比を使った解法
逆比を使った解法は次のようになります。

まず、逆比で、行きと帰りにかかった時間の比を求めて、その後、道のりの比を求めて解きます。
次に、面積図をかいて考えてみましょう。
面積図を使った解法
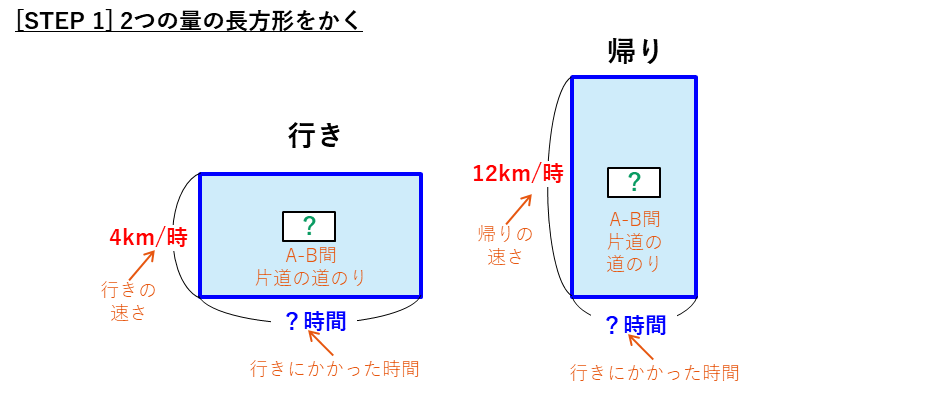
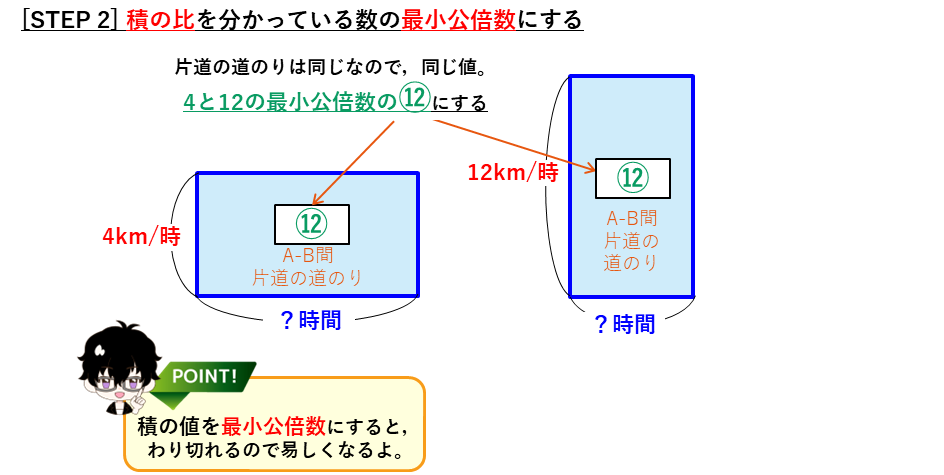
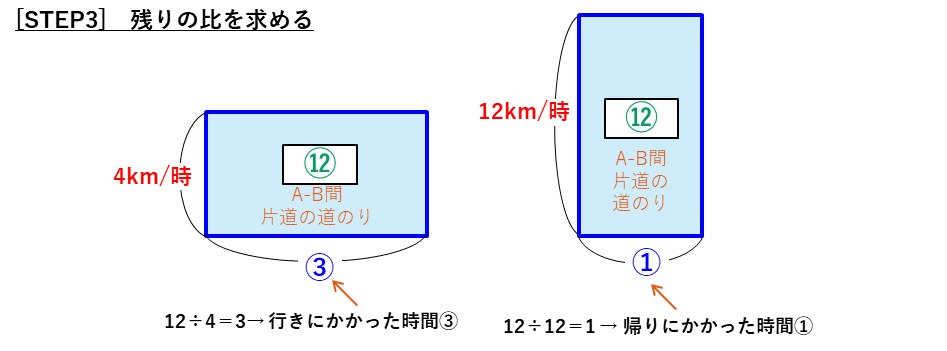
ここまでで、道のりの比、行きと帰りの時間の比が分かったので、逆比を使った解法と同じように平均の速さを求めることができます。

図をかくことで逆比を使わないでも解くことができます。比べてみると、
・逆比では、行きと帰りの時間の比を先に求めたあと、道のりの比を計算
しているのに対して、
・面積図では、道のりの比を先に決めたあと、行きと帰りの時間の比を計算
しました。順番がことなりますが、同じ内容になっていることが分かると思います。面積図では積の比ファーストで解きます。
仕事算
仕事算では、
全体の仕事量=単位時間あたりの仕事量×時間
という積の式ができます。

残りの逆比の問題の特徴を確認しましょう。

逆比を使った解法
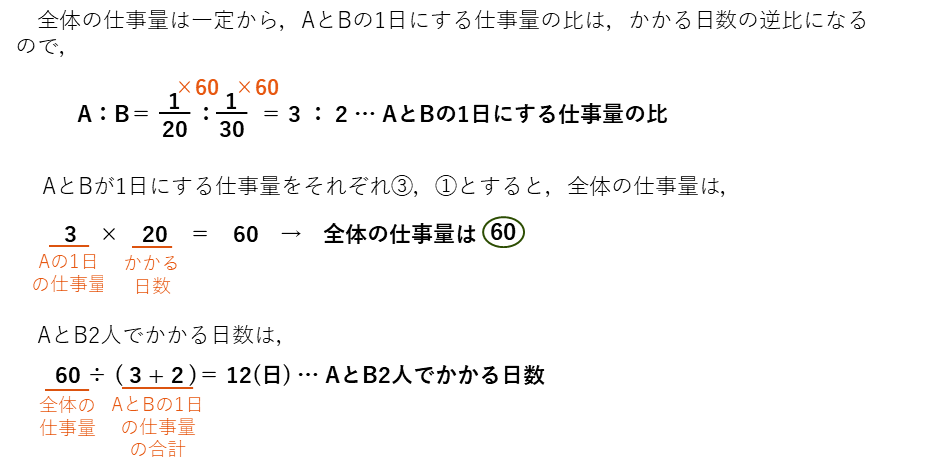
面積図を使った解法
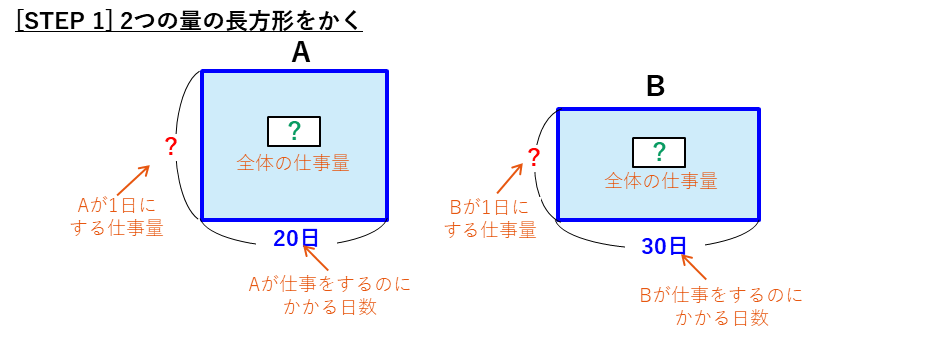
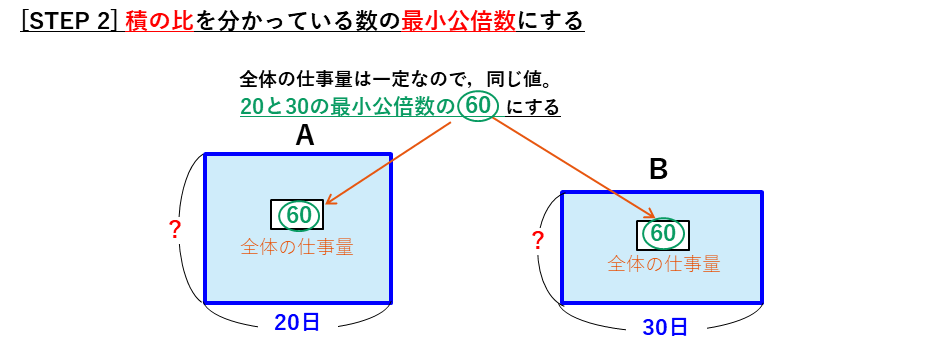
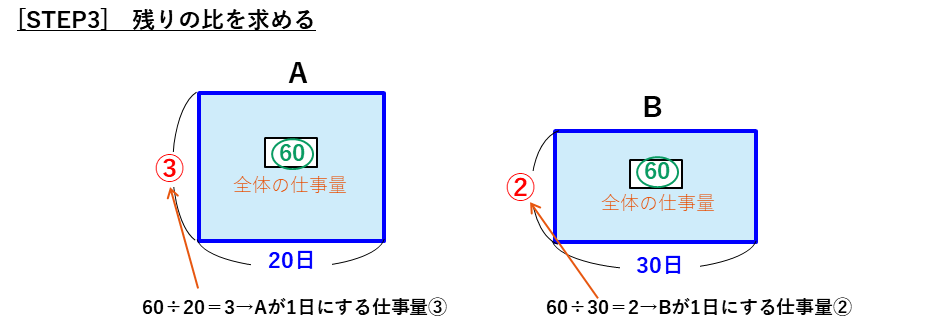

ほかにも、
・(5年下 第11回練習問題1⃣)仕事算ー仕事量を比で表す・途中で仕事量が変わる
・(5年下 第11回練習問題2⃣)仕事算ー仕事量を比で表す・周期算で解く
など、逆比を使う仕事算の問題がありますので、解いてみましょう。
歯車
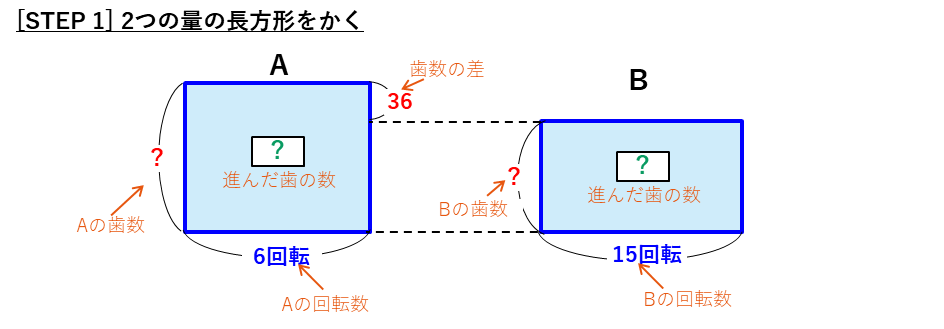
かみ合った歯車が回転する問題です。

歯車の問題では、
進んだ歯の数=歯車の歯の数×回転数
という積の式ができます。
逆比の問題の特徴を確認します。

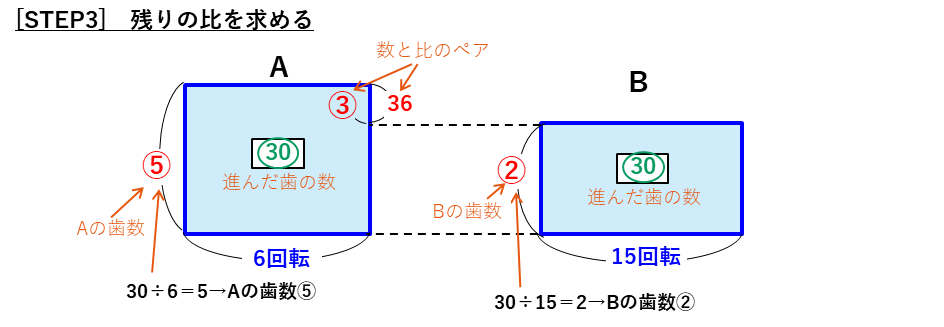
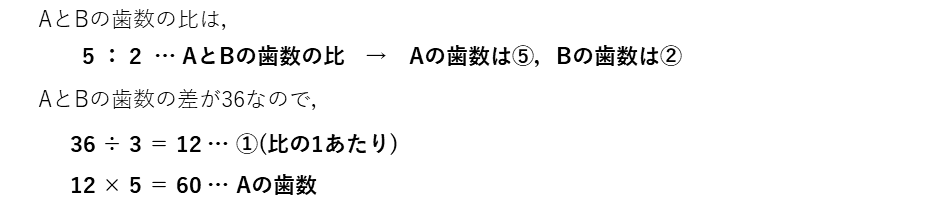
面積図を使った解法
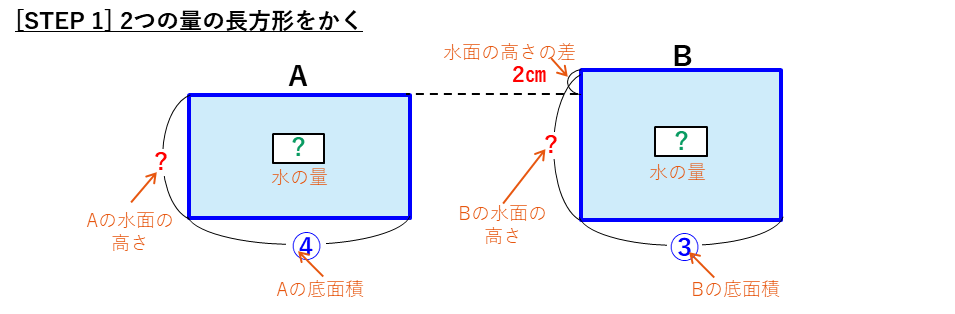
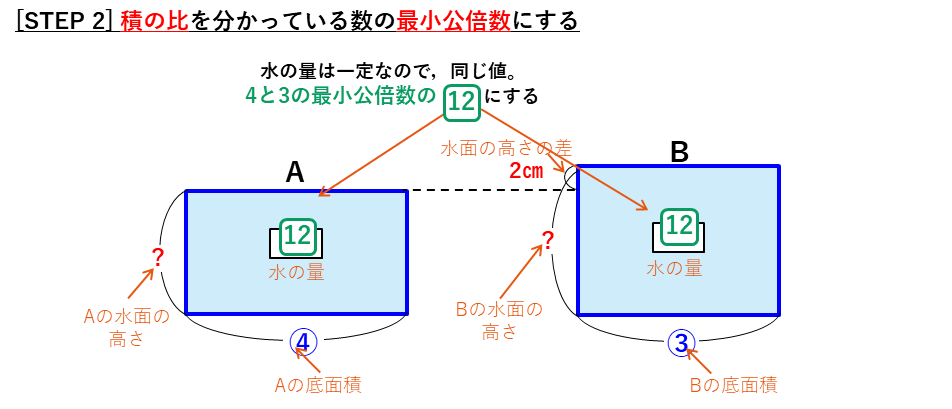
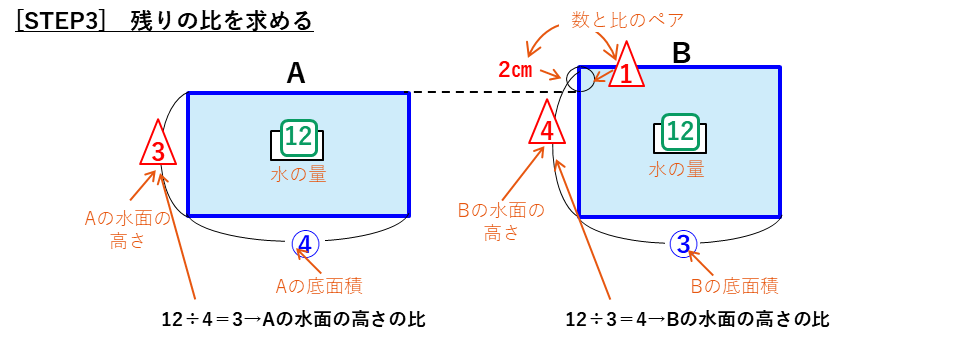
水の深さ(水面の高さ)
水の深さに関する問題です。

水の深さの問題では、
水の体積=水位(水の深さ)×底面積
という積の式ができます。
問題文から、逆比の問題の特徴を確認します。

面積図を使った解法

ニュートン算
ニュートン算は,
・水がわき出る泉の水をポンプでくみ出す
・行列に次々ならぶ人を入場口から中に入れる
など,増えていくのと減っていくのが同時におこることを考える問題です。
ニュートン算では,2つ以上の場合があり,それらを比べる問題が出題されます。全体の量に注目して線分図で解く方法(参考:予習シリーズ5年下第11回)がありますが、逆比を使わないと解けない問題もあります(難関校対策:予習シリーズ5年下第11回例題8、練習問題6⃣) 。このような難問では、面積図の解法を使うことで,よりイメージを持って解くことができます。
まずは,ニュートン算の面積図による解法を簡単にまとめます。より詳しい解説は、四谷大塚 予習シリーズ練習問題解説(5年下 第11回仕事に関する問題) ニュートン算を参照してください。
ニュートン算の面積図
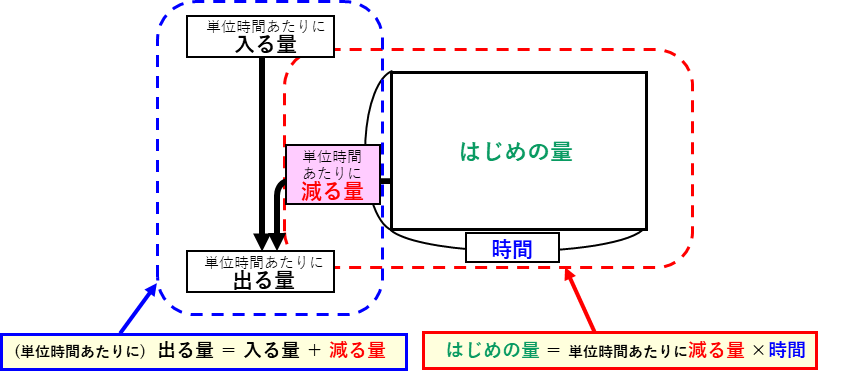
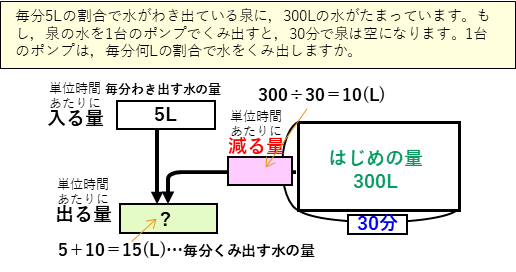
このように、ニュートン算では、
はじめの量=単位時間あたりに減る量×時間
という積の式があります。では、実際の問題を考えてみます。
面積図で解くニュートン算の例題①

問題文から、逆比の問題の特徴を確認します。

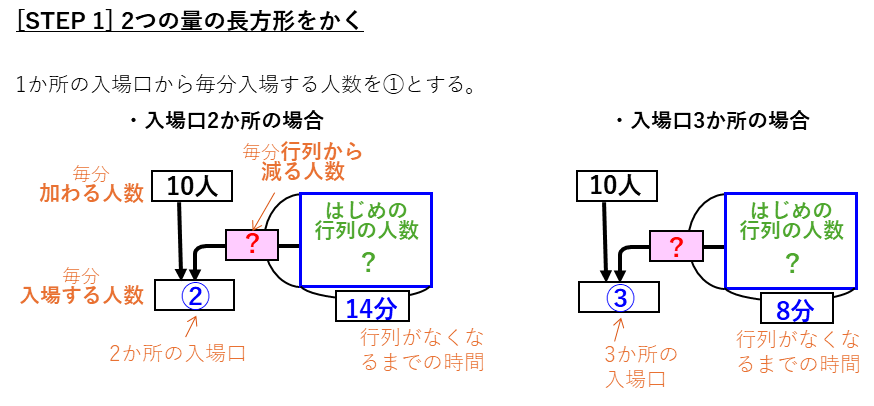
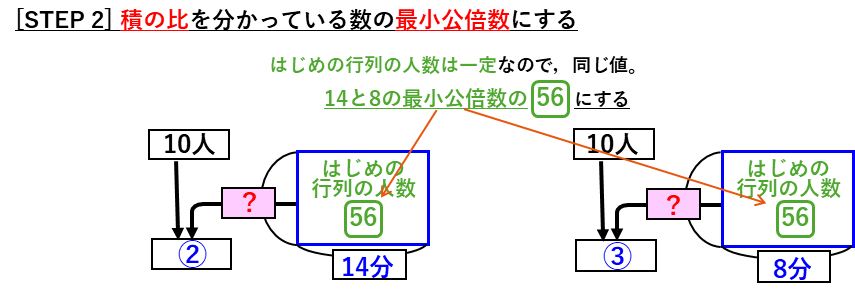
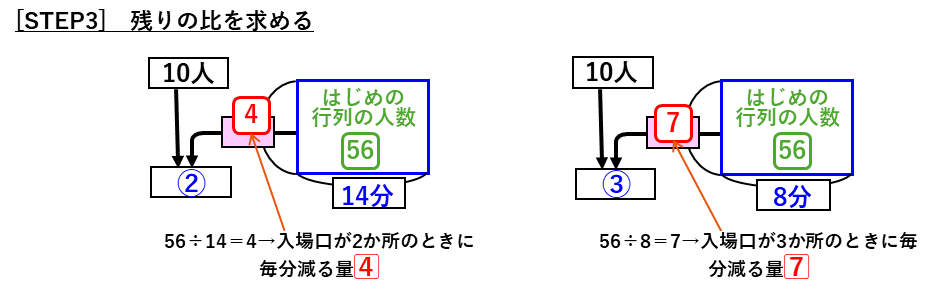
ここまでで、はじめの行列の人数と減る量の比が分かりました。ここから、面積図の左側の入場する人数の部分、
毎分入場する人数 = 毎分加わる人数(10人) + はじめの行列から毎分減る人数
から、2つの場合の差を考えます。分かりづらい場合は、線分図をかいて整理しましょう。
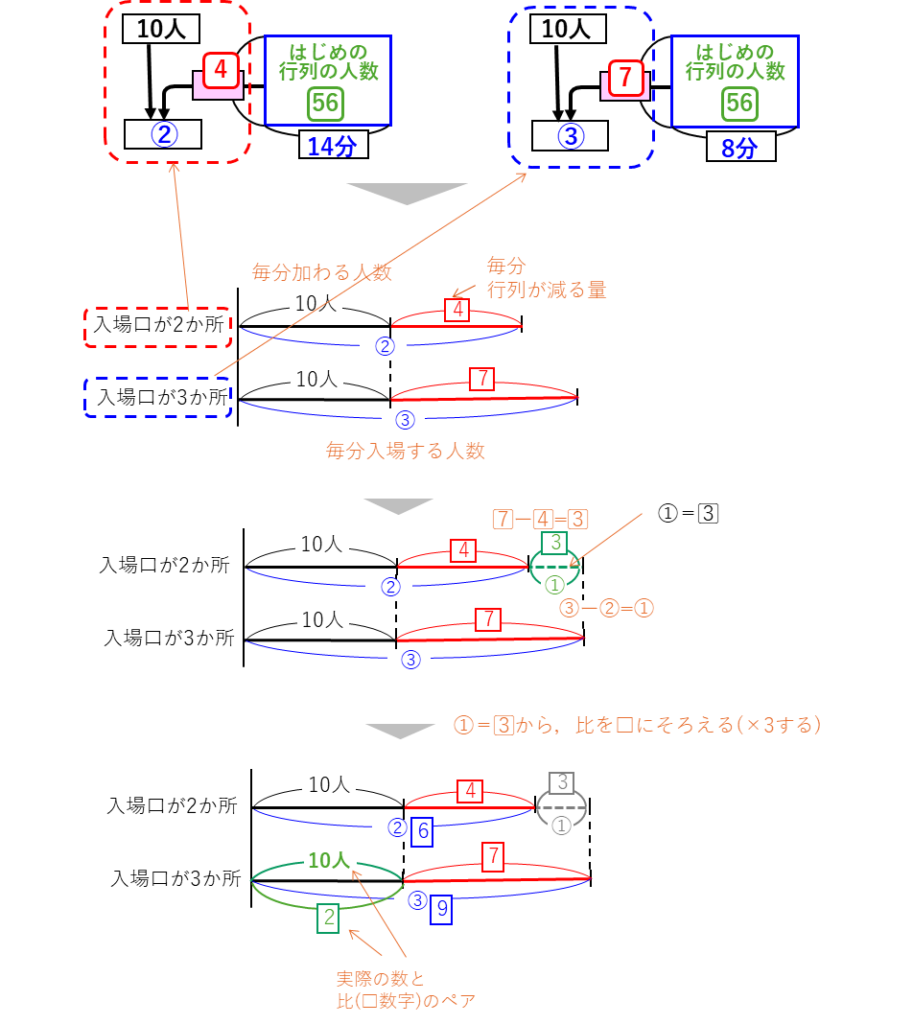
実際の数10人と比(2⃣)のペアができたので、以下のようになります。

この例題については、全体の量に注目した線分図でも解くことができますが、次の問題は逆比を使わないと解けない問題です。
面積図で解くニュートン算の例題②ー逆比を使わないと解けない


この問題は、A管、B管から入る量も、穴から出る量も分かっていません。全体の量を考えるヒントがありませんので、「1分間に増える容器の水の量」に注目して解くことになります。この場合は、面積図をかいて考えていきます。
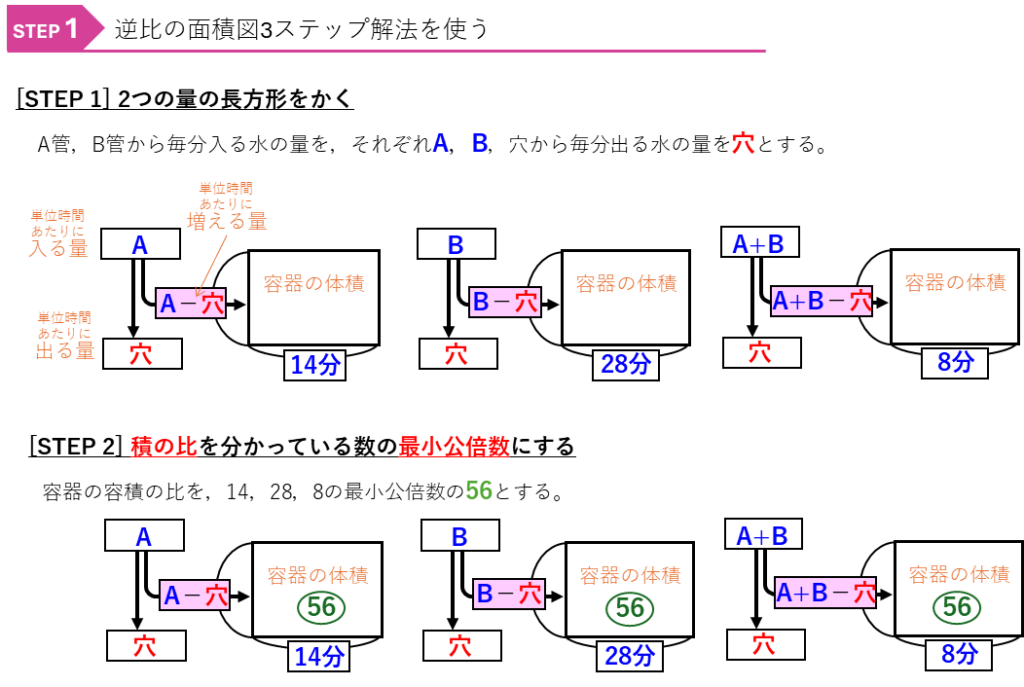
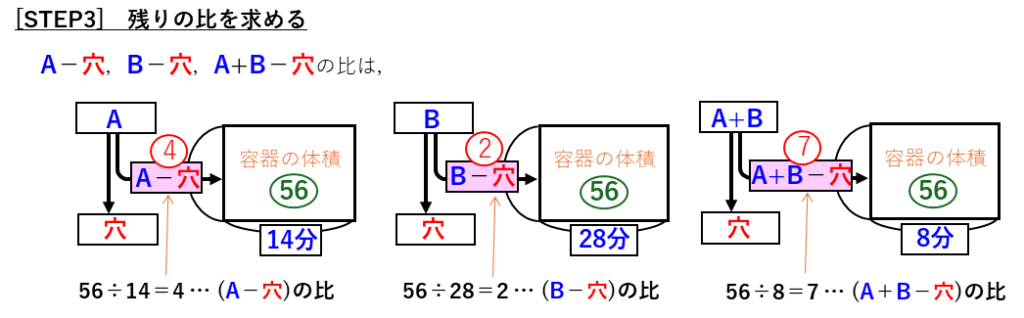
ここまでで、3つの場合(A管だけ、B管だけ、A管とB管両方)での、「1分間に増える容器の水の量」の比が分かりました。次に、それぞれの場合の差に注目して、A管、B管から1分間に入る水の量の比を求めましょう。

これで、A管、B管から1分間に入る水の量の比は、それぞれ5と3になることが分かりました。最後に、穴をふさいで、A管とB管両方を使ったときに、満水になるまでの時間を求めましょう。ここでもニュートン算の面積図をかくと分かりやすいです。
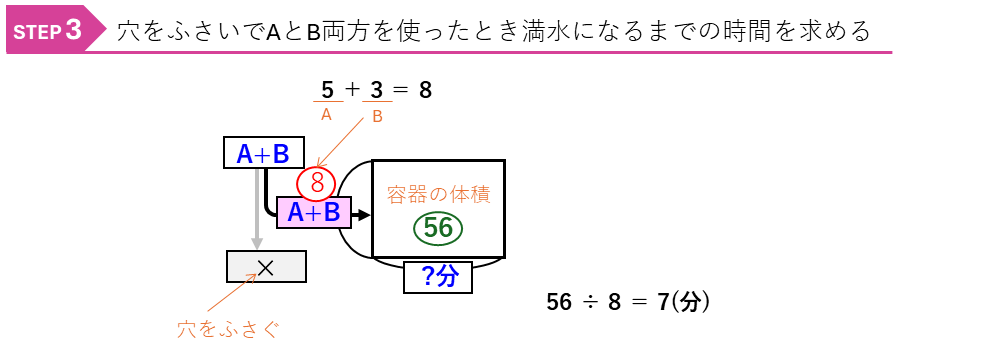
このほかにも、
・(5年下 第11回練習問題5⃣) ニュートン算ーポンプで泉の水をくみ出す
・(5年下 第11回練習問題6⃣) ニュートン算ー容器の体積・増える量を比で表す
などのニュートン算の問題がありますので、解いてみましょう。
コメント