
今回は、数に関する内容です。5年夏期講習必修編第7回「素因数分解」で習った素因数分解のやり方と、約数の個数の求め方を使った問題をより深く学習していきます。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
素因数分解
素因数分解は、ある整数を素数だけの積で表すことです。素因数分解には、連除法と同じ記号をかいて素数でわっていく方法が使われます。
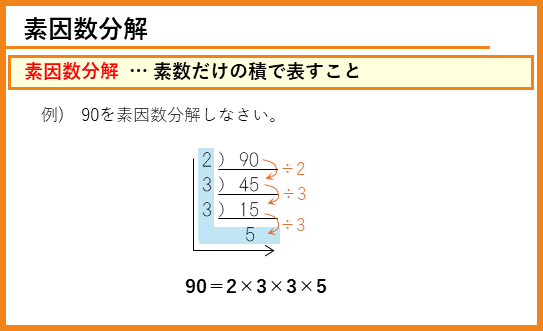
素因数分解と約数の個数
素因数分解の結果から、約数の個数を求めることができます。

約数の個数が1~4個になる数
約数の個数が1~4個になるのは、次のような数です。これらは覚えておきましょう。

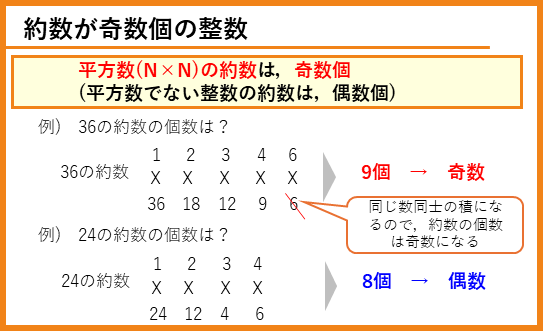
約数の個数が奇数個になる整数
約数の数が奇数個になるのは、平方数(N×N)です。平方数でない整数の約数は、偶数個になります。
最大公約数と最小公倍数から数を求める問題
最大公約数と最小公倍数の値がわかっていて、それから元の数を求める問題では、連除法で表して、式をを作って考えましょう。

既約分数の個数を求める問題
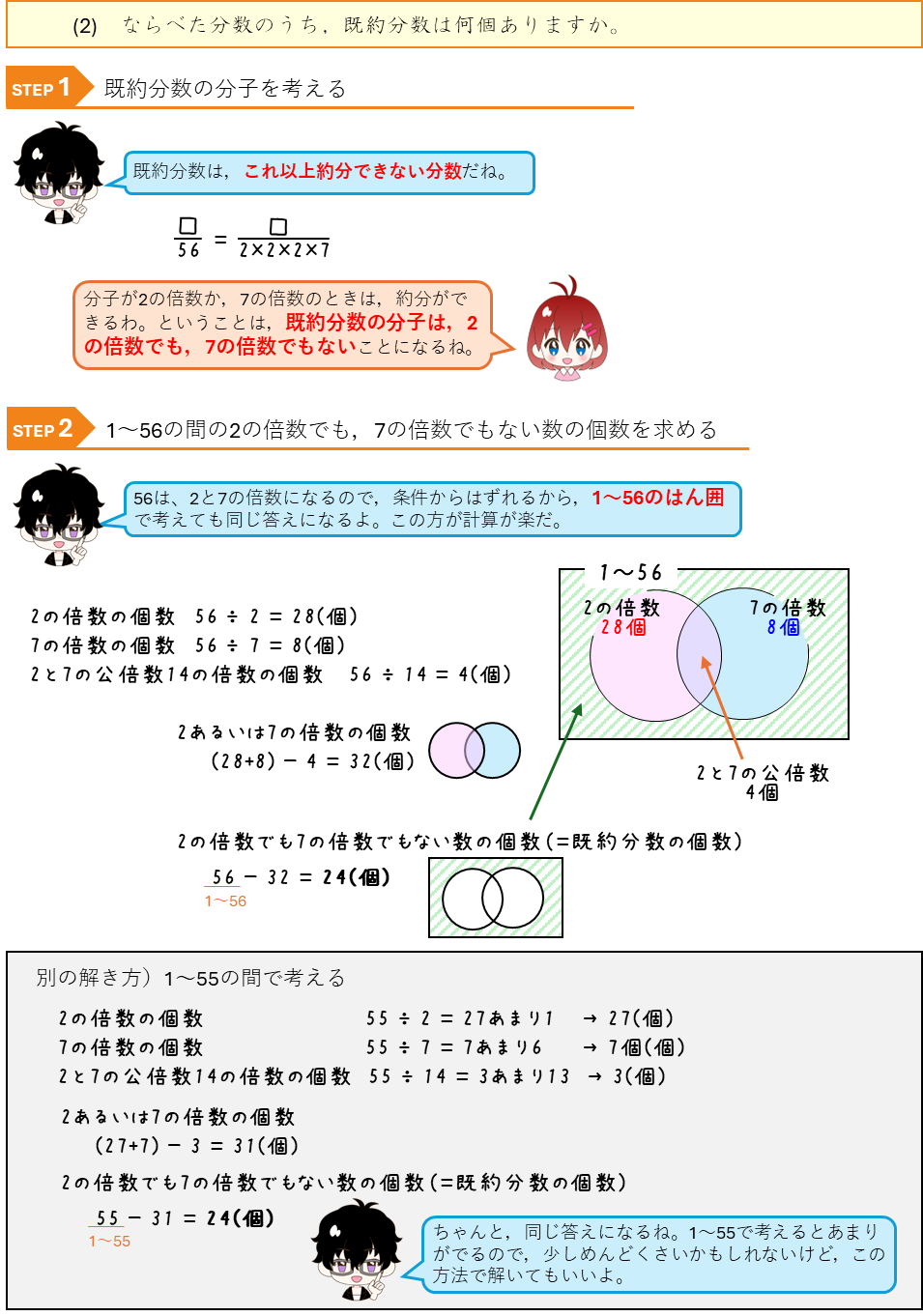
既約分数は、それ以上約分できない分数です。分母と分子の公約数は1だけです。したがって、分子は、分母を素因数分解した結果の素数の倍数ではないことになります。
例えば、$\frac{□}{96}$という分数を考えると、分母の96は、
96=2×2×2×2×2×3
と素因数分解できます。既約分数となるのは、
□が2の倍数でも3の倍数でもない
ときです。既約分数を求める問題では、この条件の分子の個数を求めます。

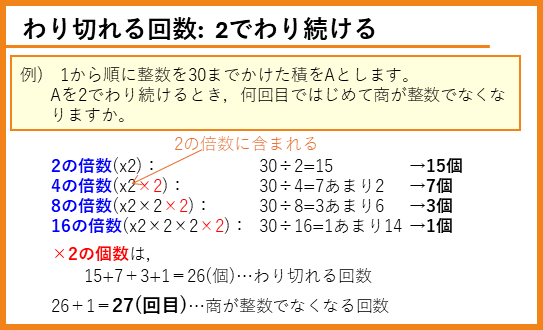
わり切れる回数
24を素因数分解すると、
24=2×2×2×3
となり、2が3個あるので、2でわったときに3回までわり切れます。別の言い方をすると、4回目にはじめて商が整数でなくなります。
わり切れる回数や、はじめて商が整数でなくなる回数を求める問題では、素因数分解をして、わる数が何個あるかを求めて解きます。

練習問題
既約分数の個数

最大公約数と最小公倍数から求める
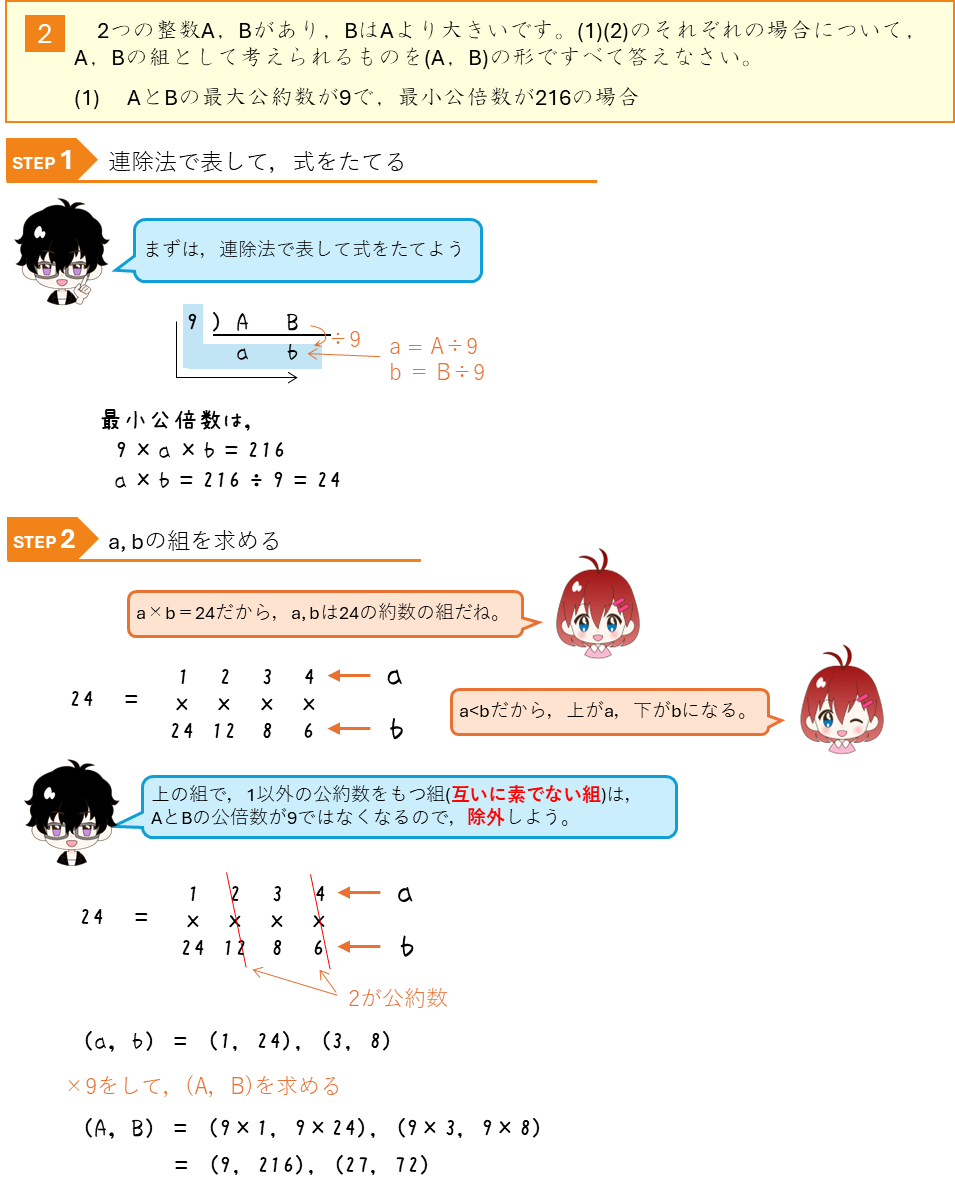
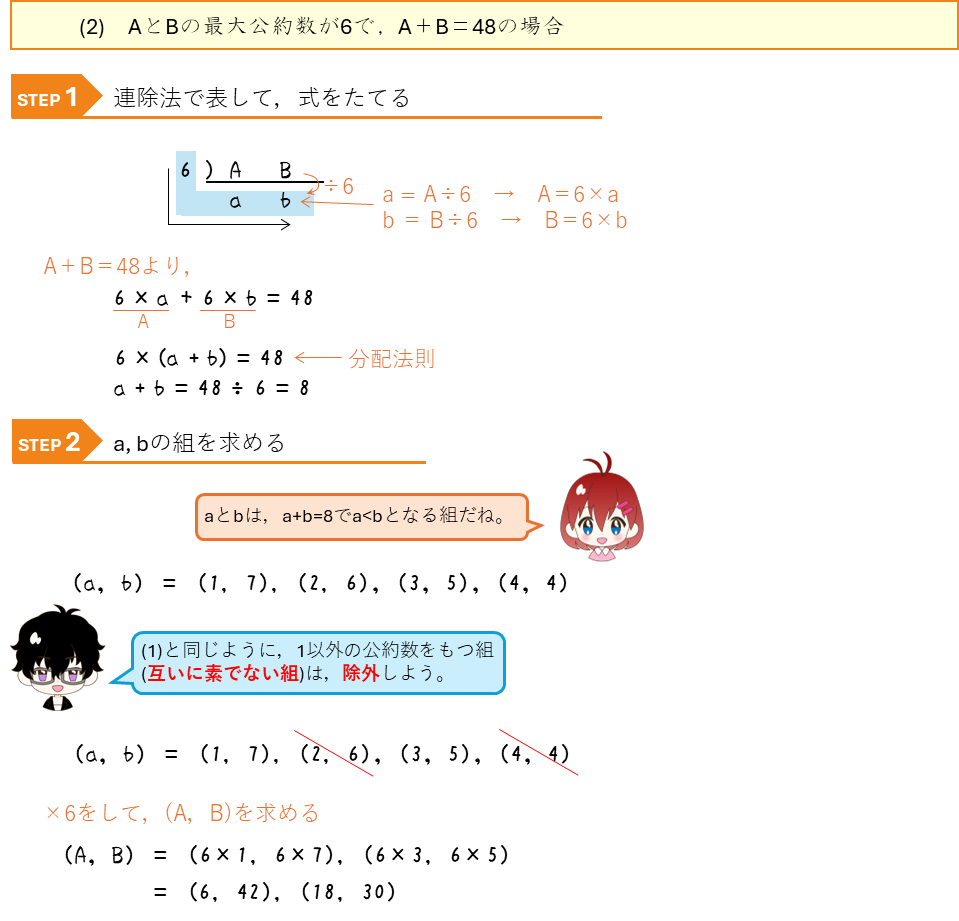
いろいろな約数の個数
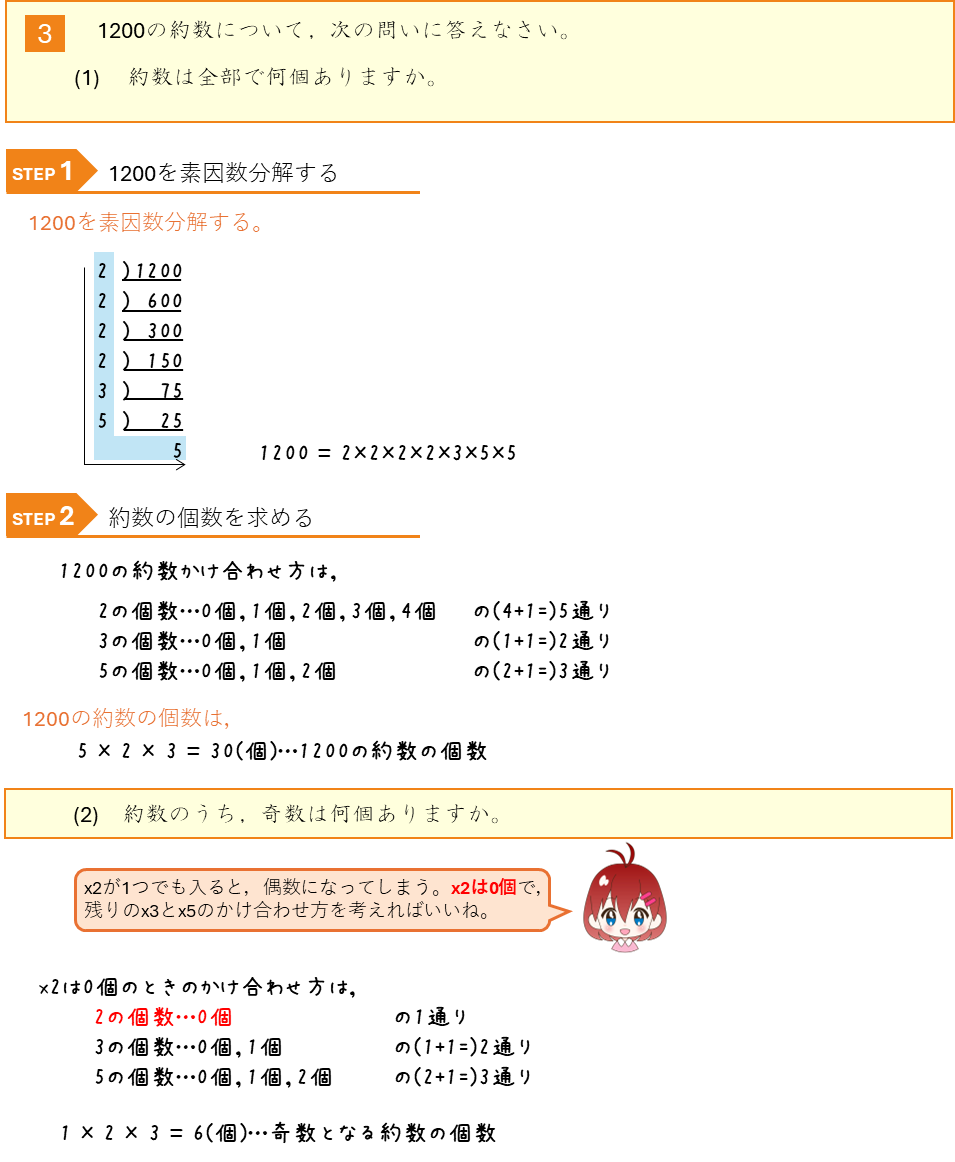

約数の個数が奇数や4個になる

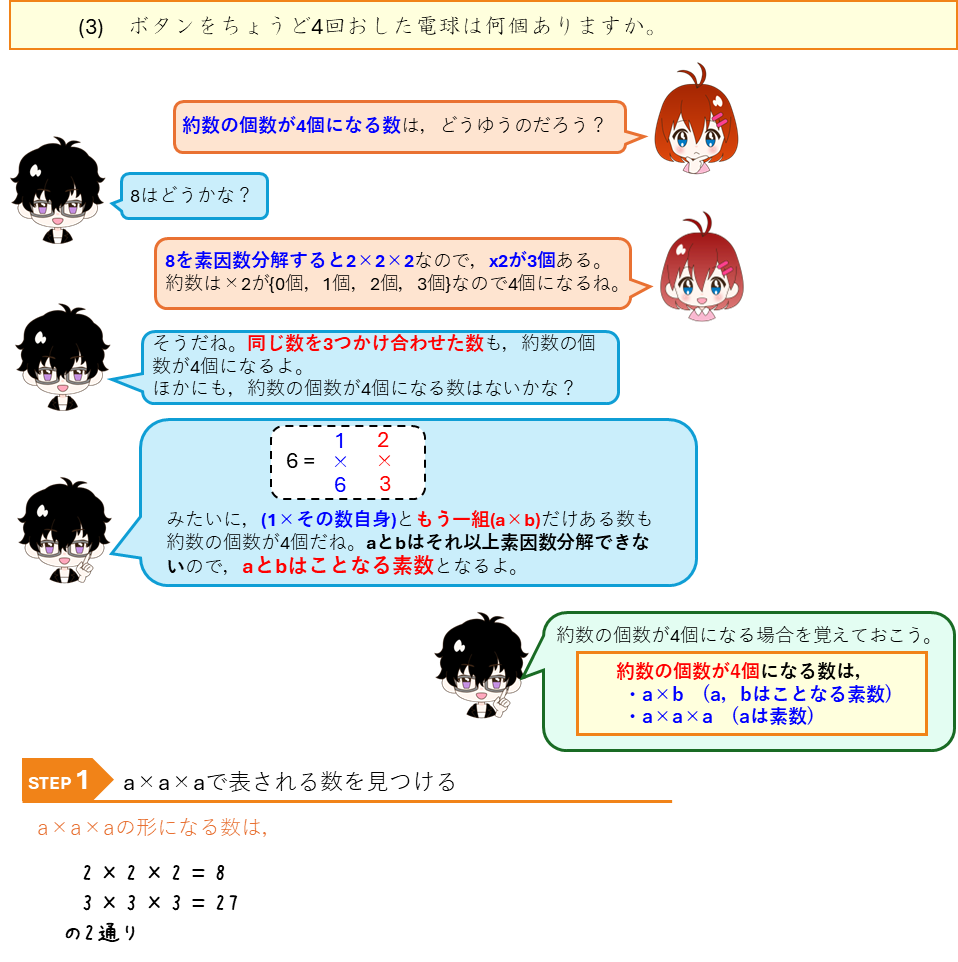

この問題では素数を小さい順の書き出しました。1~19までの8個はすぐわかるように、しっかり覚えておきましょう。100までの素数の判定方法は次の記事を参考にしてください。
わり切れる回数




コメント