
今回は、「速さ」について勉強します。生活の中でも自動車や電車の速さが時速何kmということがあるかと思います。時速は、1時間に進むきょり(道のり)です。これだけではなくて、1分間に進むきょりを表す分速、1秒間に進むきょりを表す秒速もでてきます。
このように、速さは、1時間、1分間、1秒間に(単位時間あたりに)進むきょりです。したがって、次のような式になります。
速さ = きょり ÷ 時間
きょりと時間が分かれば速さを計算できます。また、きょりや時間を求める問題もでてきます。
速さは、時速?km、分速?m、秒速?m、秒速?㎝のように、時間の単位と長さの単位がいろいろあります。これらの単位を変換する問題がでます。速さは、時間と長さの2つの単位が組み合わさっているので、複雑になります。慣れないうちは、まずは長さをそろえる、次に時間をそろえるなど、1つずつ計算しましょう。
速さは、旅人算、通過算、流水算、時計算などの特殊算やグラフの問題など、さまざまな問題に出てきます。基本をしっかりと身につけて、得意な単元にしましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
速さとは
速さは、単位時間(1時間、1分、1秒)あたりに進むきょり(道のり)です。

になります。簡単な例を示します。

速さの定義から、きょりと時間がわかれば、速さは次の式で求めることができます。

単位の変かん
速さには、時速?km、分速?m、秒速?mや秒速?cmのように、時間の単位と長さの単位の組み合わせによって、いろいろな単位があります。問題を解く途中でこれらの単位をそろえるなど、単位を変かんする必要があります。
時間の単位変かん
1時間は60分、1分は60秒から、次のように時間の単位を変換します。
・時間→分/分→秒
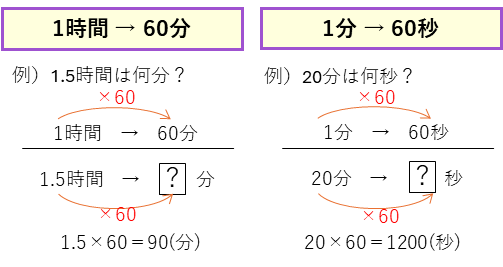
・時間→分/分→秒
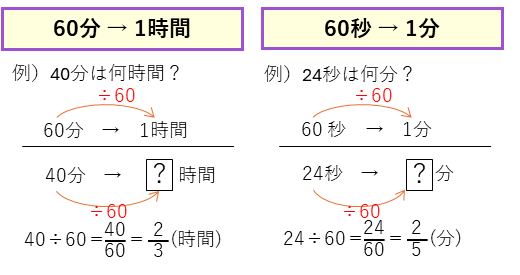
長さの単位変換
1kmは1000m、1mは100cmから、長さの単位は次のように変かんします。
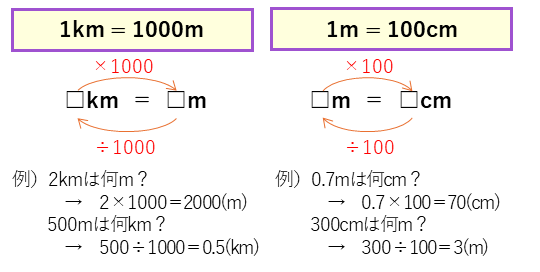
速さの単位変換
秒速から分速に変換する場合、分速は60秒間に進むきょりになるので、分速は秒速の60倍(×60)
になります。同じように、
分速から時速に変換する場合、時速は60分間に進むきょりなので、時速は分速の60倍(×60)
になります。 逆に、
分速から秒速への変換では、秒速は$\frac{1}{60}$分間に進むきょりなので、秒速は分速の$\frac{1}{60}$(÷60)、
時速から分速への変換も同じように分速は$\frac{1}{60}$時間に進むきょりなので、分速は時速$\frac{1}{60}$(÷60)
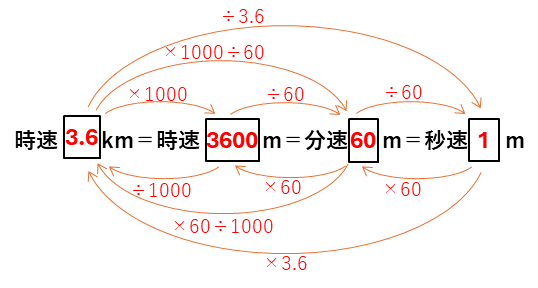
で計算できます。まずはこの関係をしっかり覚えましょう。この計算を図でかくと次のようになります。
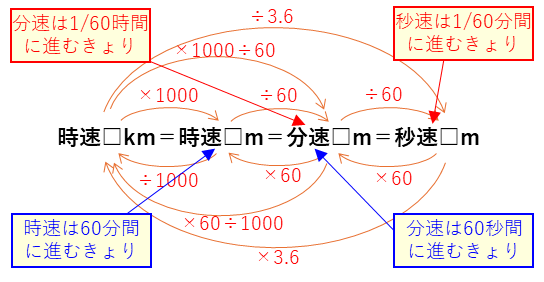
時速の長さの単位はkm、分速の長さの単位はmの場合が多いです。
時速□kmを分速□mに直す場合は、×1000÷60
分速□mを時速□kmに直す場合には、×60÷1000
とkmとmの変換も行います。慣れるまでは、時速□mに変かんすると分かりやすいです。
秒速1mの例を示します。
速さの公式
きょり(道のり)、速さ、時間を求める公式です。速さに関する問題の基本ですので、しっかり覚えましょう。

まずは、簡単な例題で確認します。

実際の問題では、1より小さい小数や分数が出てくると、直感的にわかりづらくなります。その場合は、上のような例を考えて式を確認してみましょう。
他にも、公式を覚える方法があります。
「はじき」の図
速さの公式を覚える図として、有名なのは「はじき」の図です。

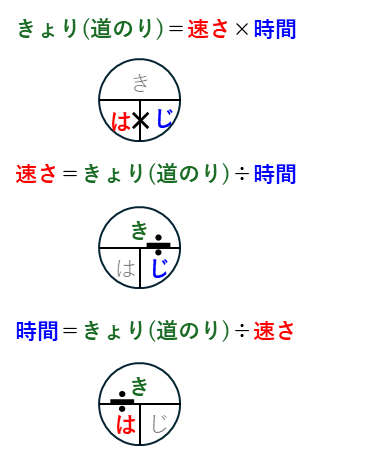
この図では、
きょりを求める場合は、”き”以外の”は(速さ)”と”じ(時間)”とそれをつなぐ”×”
が公式になります。
速さを求める場合は、”は”以外の”き(きょり)””÷””じ(時間)”、
時間を求める場合も同じように、”じ”以外の”き(きょり)””÷””は(速さ)”
が公式になります。
”き”、”は”、”じ”の位置は、「木(き)の下のはげじじい」で覚えましょう。
速さの面積図
「はじき」の図は、とても覚えやすいのですが、速さの公式の3つの関係の本質を理解しないまま、問題だけを解いてしまう危険もあります。そこで、「はじき」の図ではなくて、面積図を使うことも覚えておきましょう。
面積は、
面積 = たての長さ × 横の長さ
で求めることができます。図にかくと、
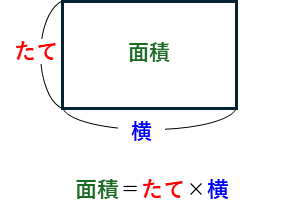
となります。また、たての長さ、横の長さを求める式は、

となります。ここで、面積→きょり、たて→速さ、横→時間、とすると、速さの面積図がかけ、面積の公式と同じように、速さの公式を考えることができます。
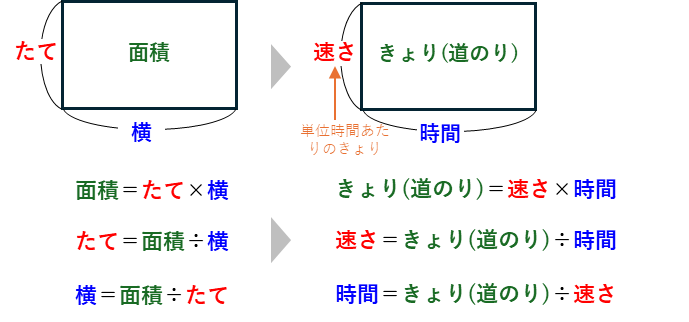
速さの公式だけでなく、積の形の公式はたくさん出てきます。面積図を使うことで、積の形の式だけをしっかり覚えておけば、他の式を作ることができます。詳しい解説は、次の記事を参照してください。
練習問題
速さー単位をそろえてきょり、時間を求める
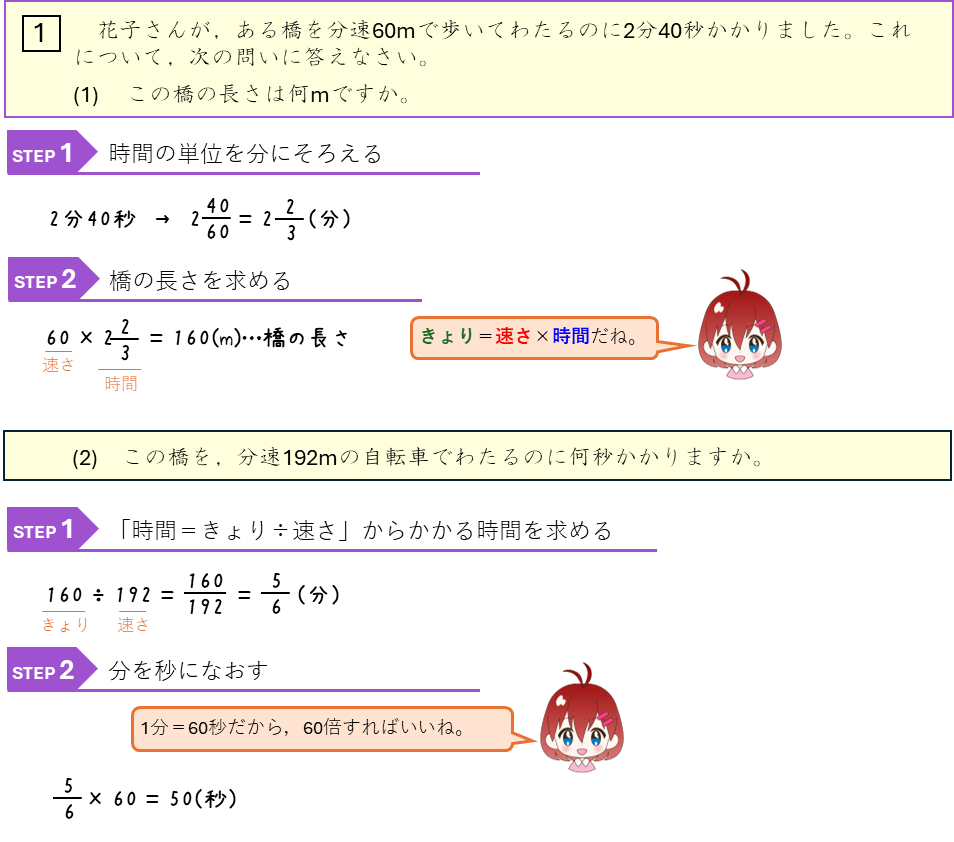
速さー時間と速さを求める①
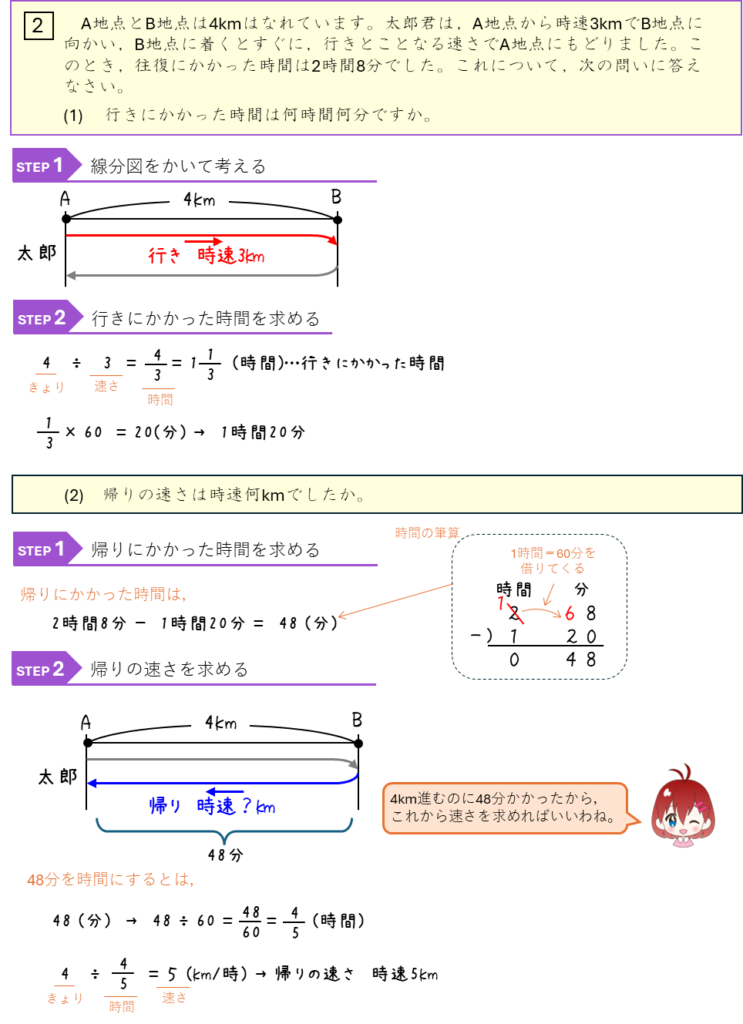
速さー時間と速さを求める②
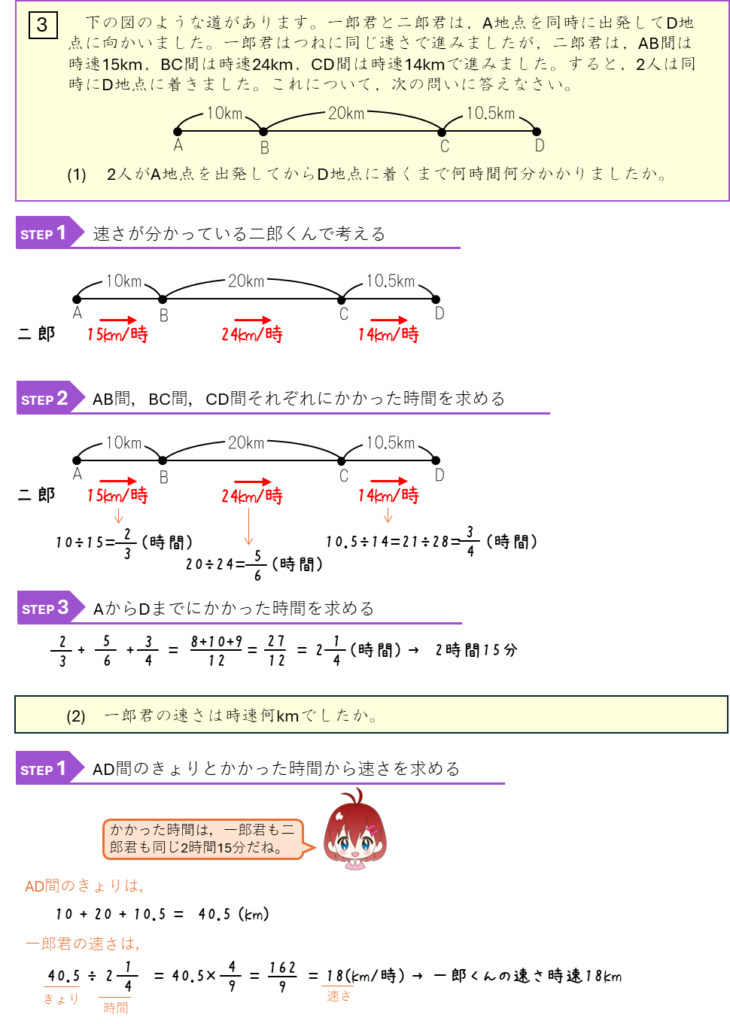
速さーわすれ物をとりに途中で引き返す
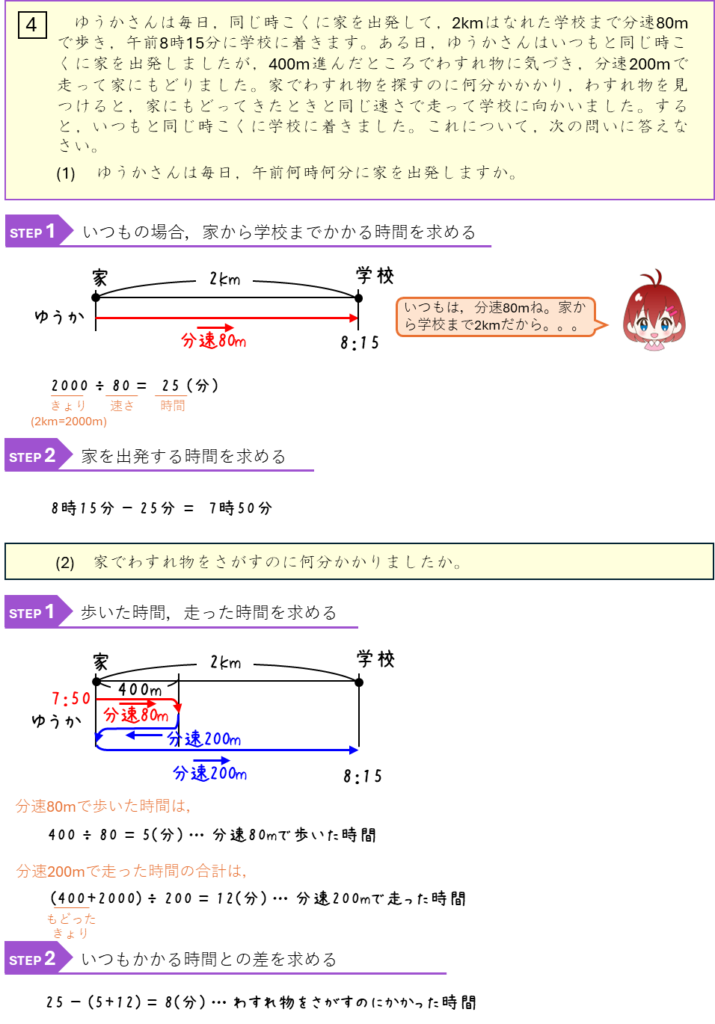
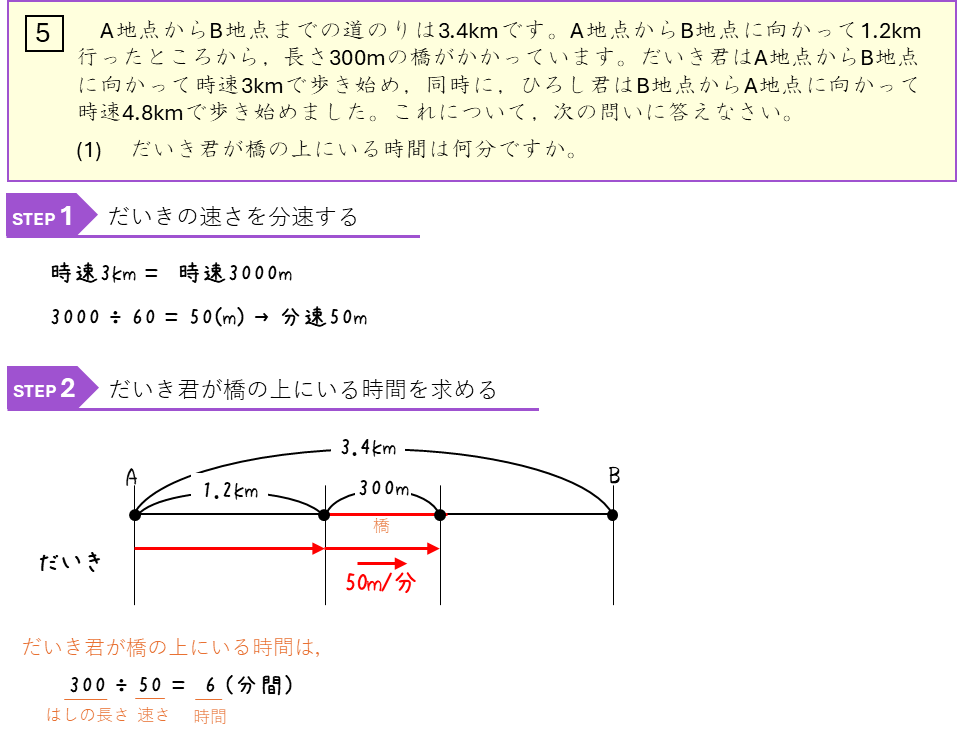
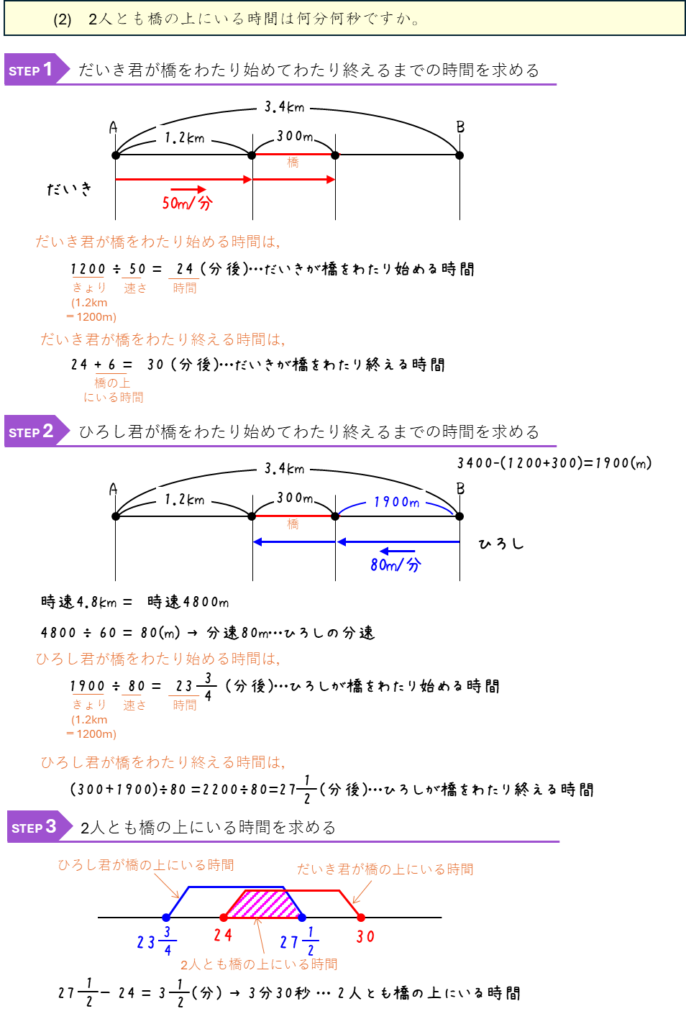
速さー途中の橋にいる時間

コメント