
前回までで、線分図の基本と4種の解法を説明しました。さあ、いよいよ特殊算を解いていきます。今回は、4年生で習う「和差算(4年上)」、「分配算(4年下)」、「やりとり(4年下)」について解説します。
線分図で解く特殊算ー和差算・分配算・やりとりの問題
和差算
和差算は、2つ以上の量の和と差の両方が分かっているとき,それらの量を求める問題です。

AとBの和が140円と差が60円と分かっています。和の値が分かっているので、「和の線分図」をかきます。

次に、線分図の解法①を使って、「長さをそろえて」解いていきます。

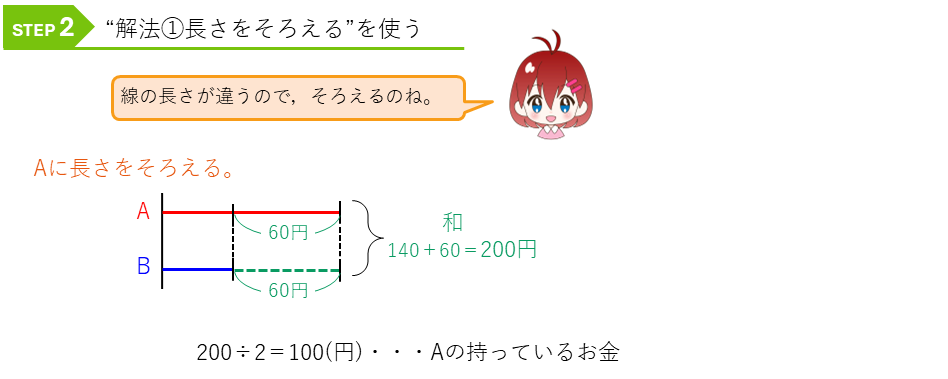
長さがそろっていれば、それらの合計を線の本数でわれば、1本あたりの長さ(量)を求めることができます。
分配算
分配算は、2つ以上の量の和や差と,?倍という関係からもとの数を求める問題です。もとにする大きさを①として線分図をかいて解きます。
分配算ー2人の合計が分かっている

Bくんがもらうお金を①とすると、Aくんがもらうお金は④となるので、これを線分図にかき入れます。
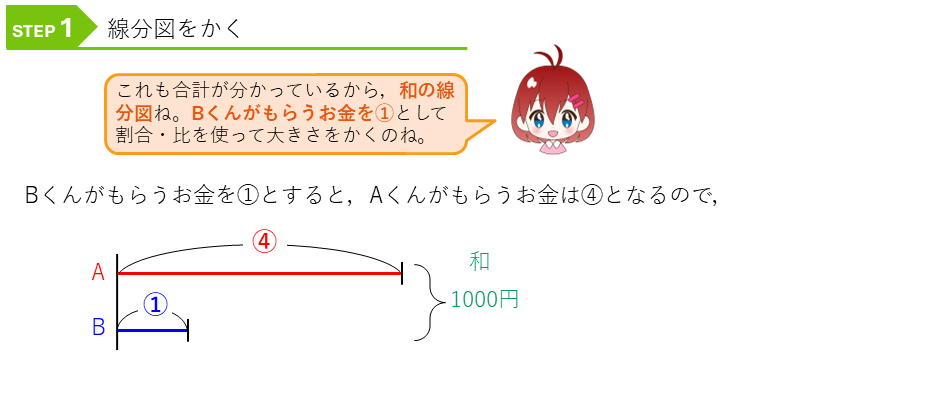

線分図の解法②で、数と丸数字のペアを見つけて解きます。

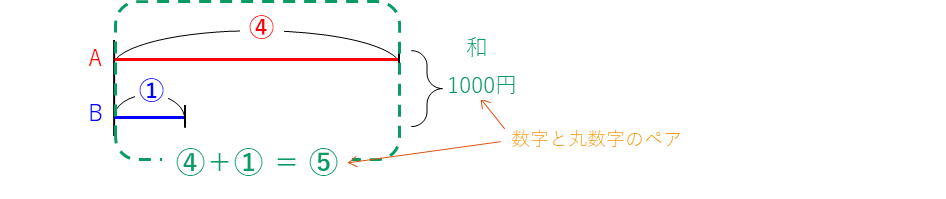

分配算ー2人の差が分かっている

今度は、AくんとBくんの差の個数が18個分かっている問題です。差の線分図になります。
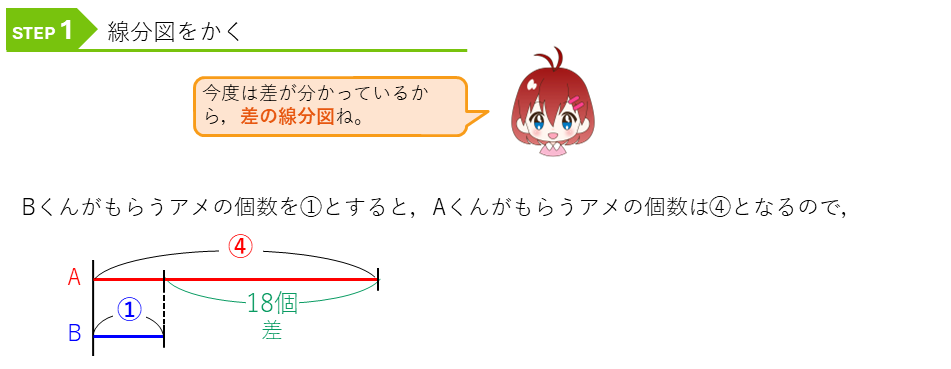
差に注目して、数と丸数字のペアのくちびるを作って解く、線分図の解法②を使います。



分配算ーはんぱがある
単純な?倍という関係ではなくて、はんぱがある問題です。

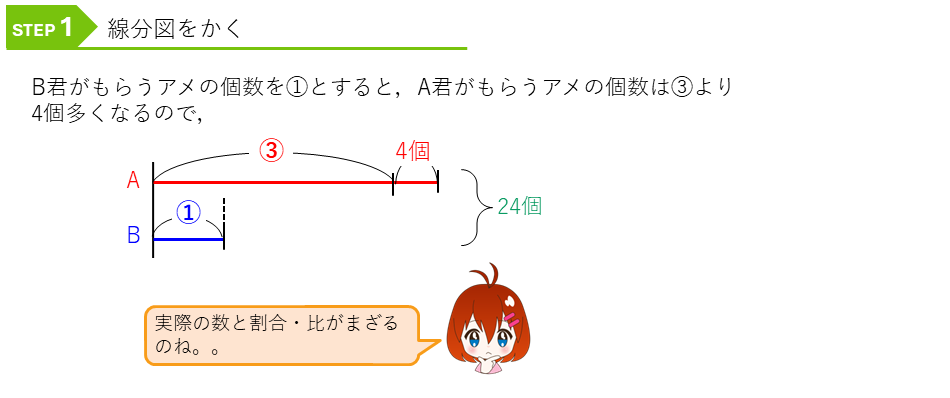
はんぱな数をのぞいて、丸数字だけにすればOKです。



やりとりの問題
お金や物をやりとりする問題では、やりとりする前とやりとりする後の違いに注目して解いていきますが、ここでは線分図を使った解法を解説していきます。
やりとりの問題ー全体の量が分かっている
最初の例題は、A君とB君の合計が分かっている問題です。

まずは、やりとりする前の線分図をかいてみましょう。
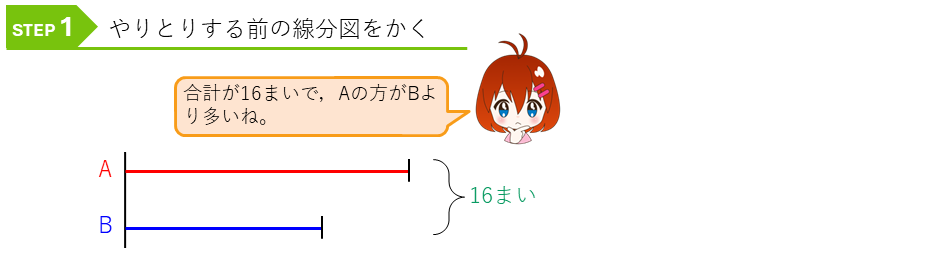
次に、やりとりした後をこの線分図にかき入れます。
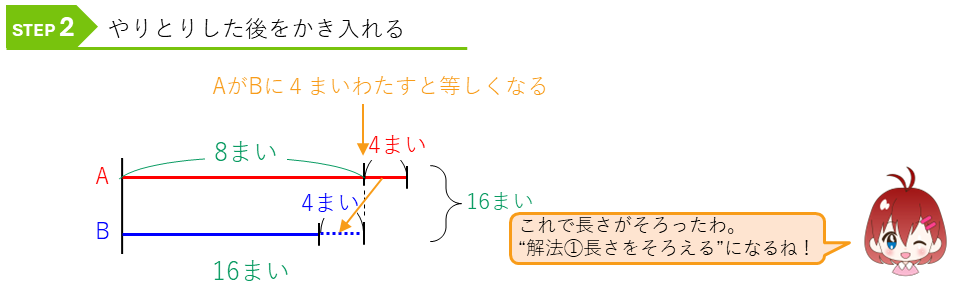
AとBの合計が分かっていて、AとBの長さをそろったので、線分図の解法①になります。

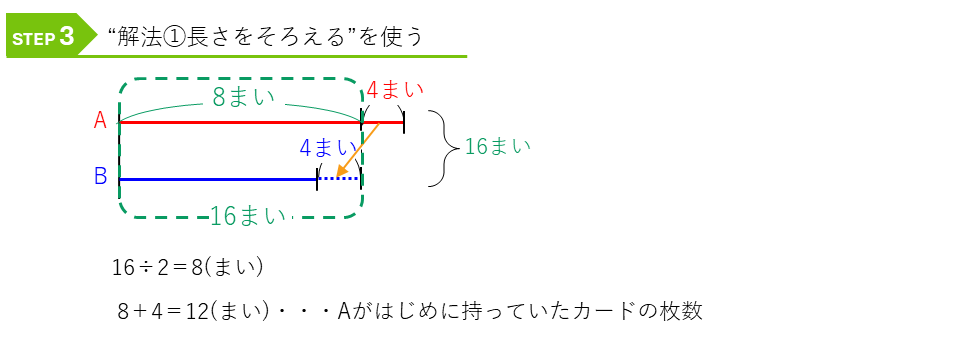
やりとりの問題ー2人がはじめに持っていたまい数の比が分かる
次の例題は、はじめにA君がB君の4倍のまい数のカードを持っていたことが分かっているケースです。

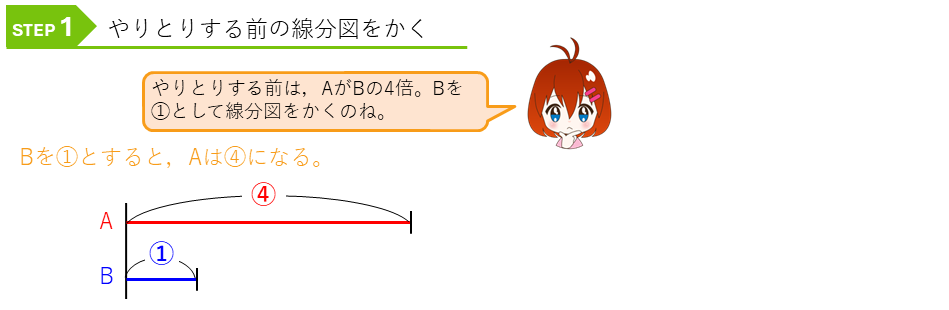
これに、やりとりした後をかき入れます。
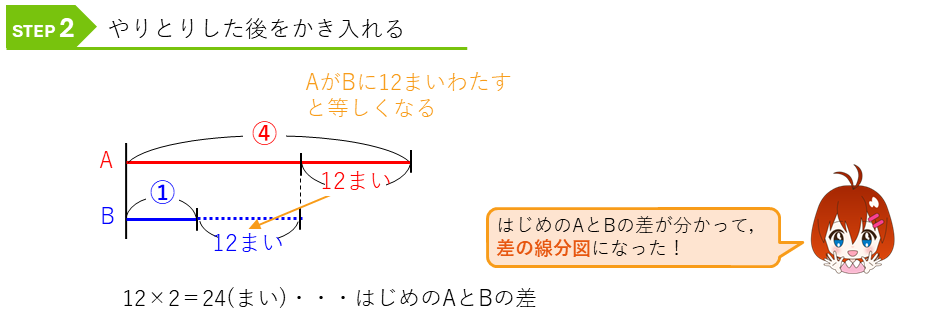
これで、はじめのAとBの差のまい数が分かりました。差に注目して、解法を使って解きましょう。

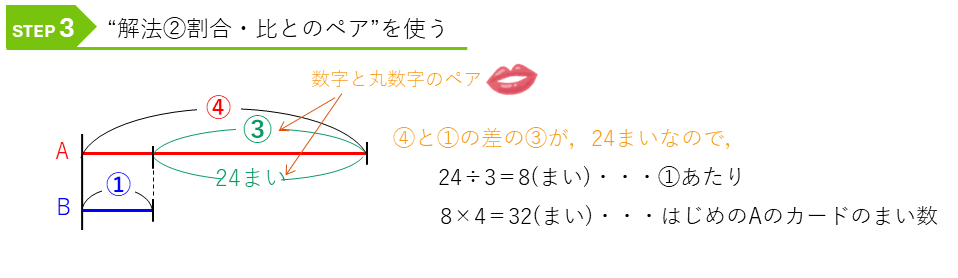

解法でうまく解けることが分かったかな?

はい。線分図をかければ、解き方が分かった気がします。

じゃあ、次回は5年生で習う特殊算にチャレンジしてみよう。
コメント