
今回も、図形について新しい内容を学習します。底辺の比と面積の比(面積比)が、高さが同じ場合に等しくなることを使った問題です。特に、「双子山」型の2つの三角形を見つけて解いていくものが多いです。練習問題からは、2つ以上の「双子山」型の三角形を見つけて、面積や底辺の長さを求めていきます。連比を使った問題も出ますので、比の計算が問題なくできるようにしましょう。
解説
高さが同じ場合の面積比
三角形の面積は、「底辺×高さ÷2」なので、高さが同じ三角形の面積の比は、底辺の比と等しくなります。特に、下のような2つの三角形がくっついた形を見つけて解く問題が多く出題されます。ここでは、「双子山型」と呼ぶことにします。
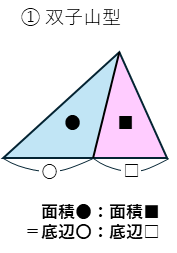
また、高さが同じ、三角形と台形に関しては、面積比は、三角形の底辺の長さと、台形の上底と下底の長さの合計の比と等しくなります。
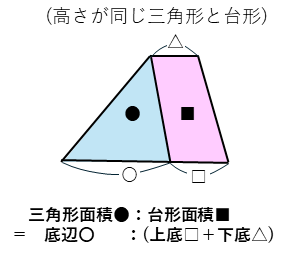
練習問題
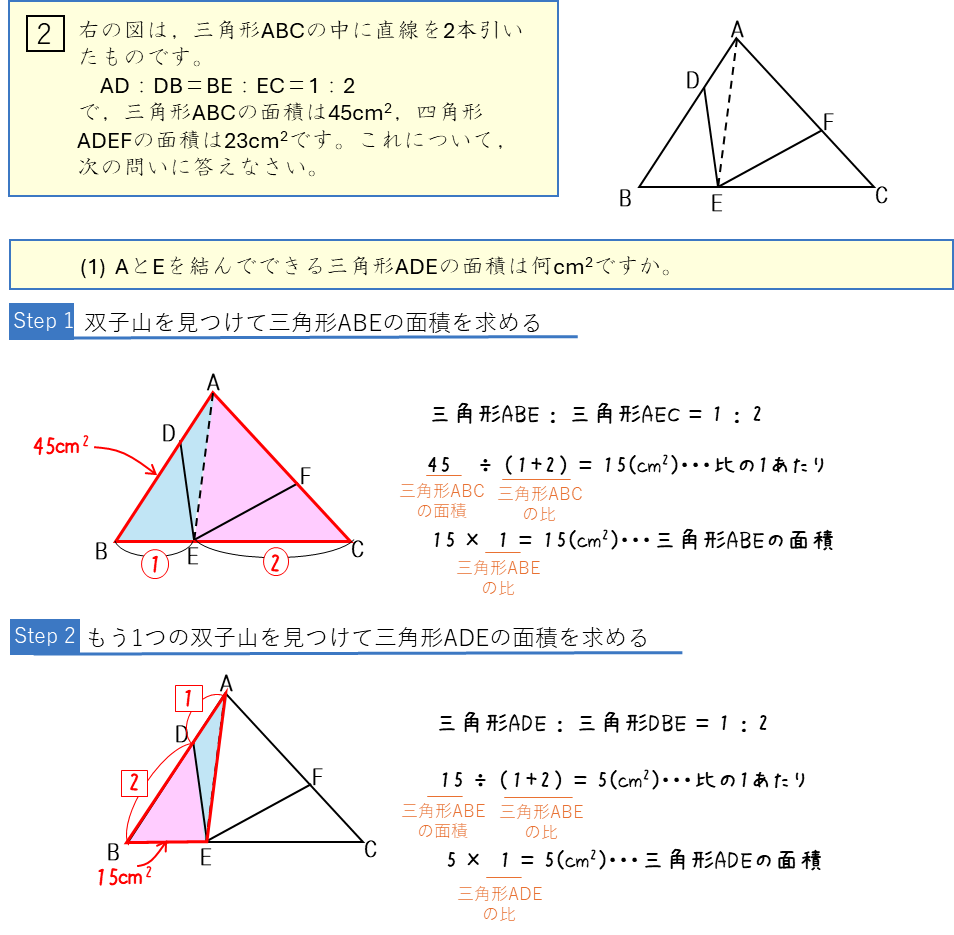
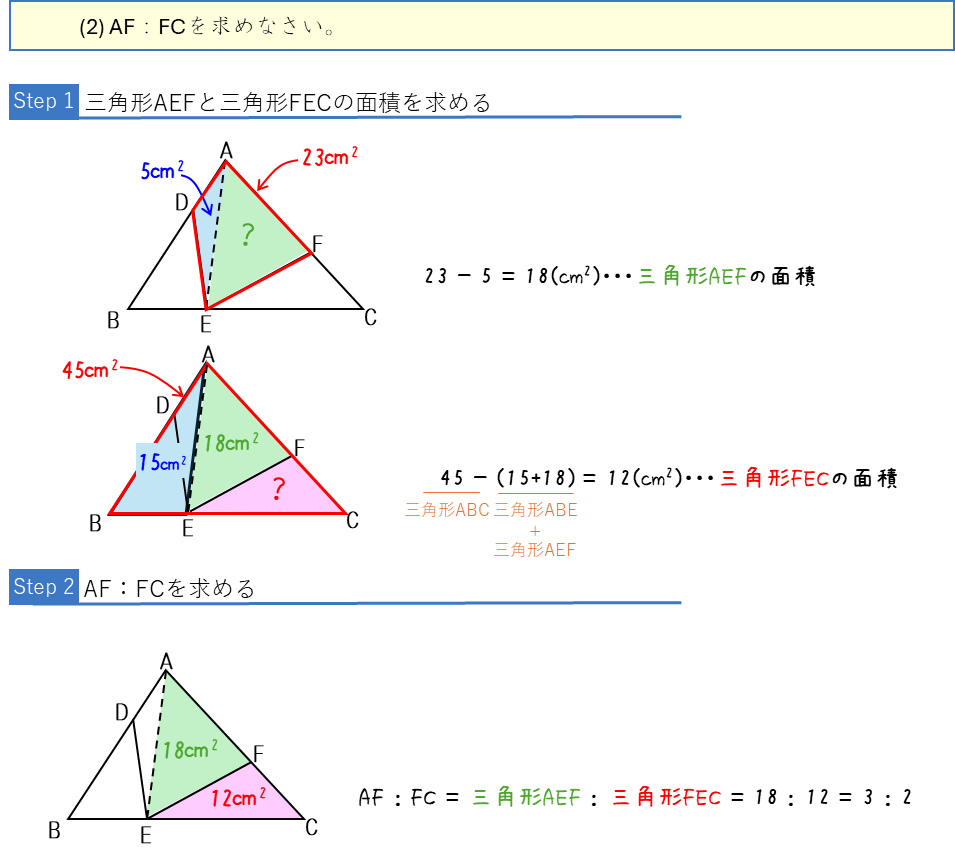
底辺の比と面積比ー2つの双子山
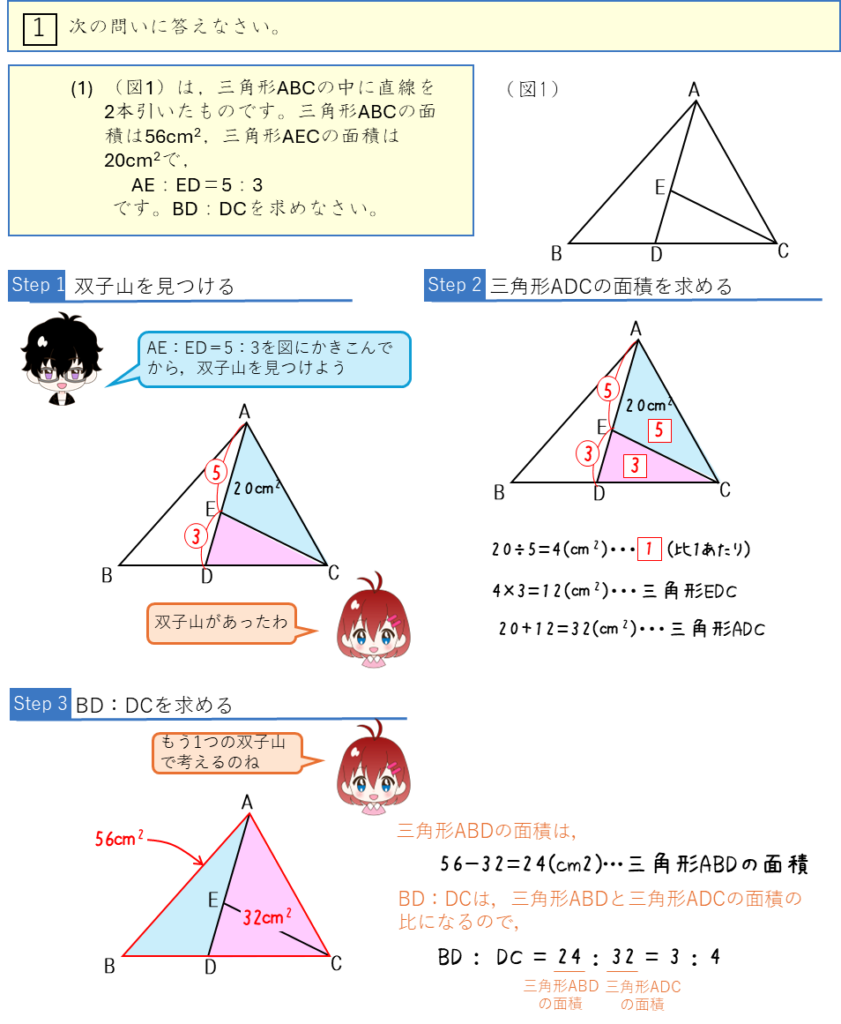
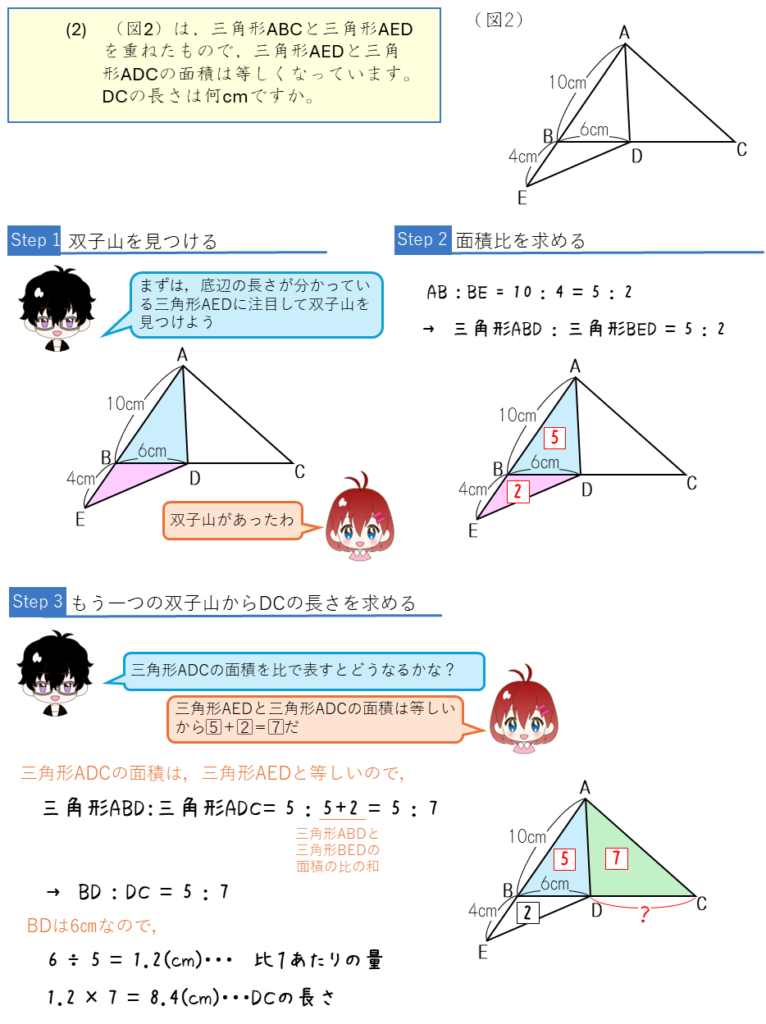
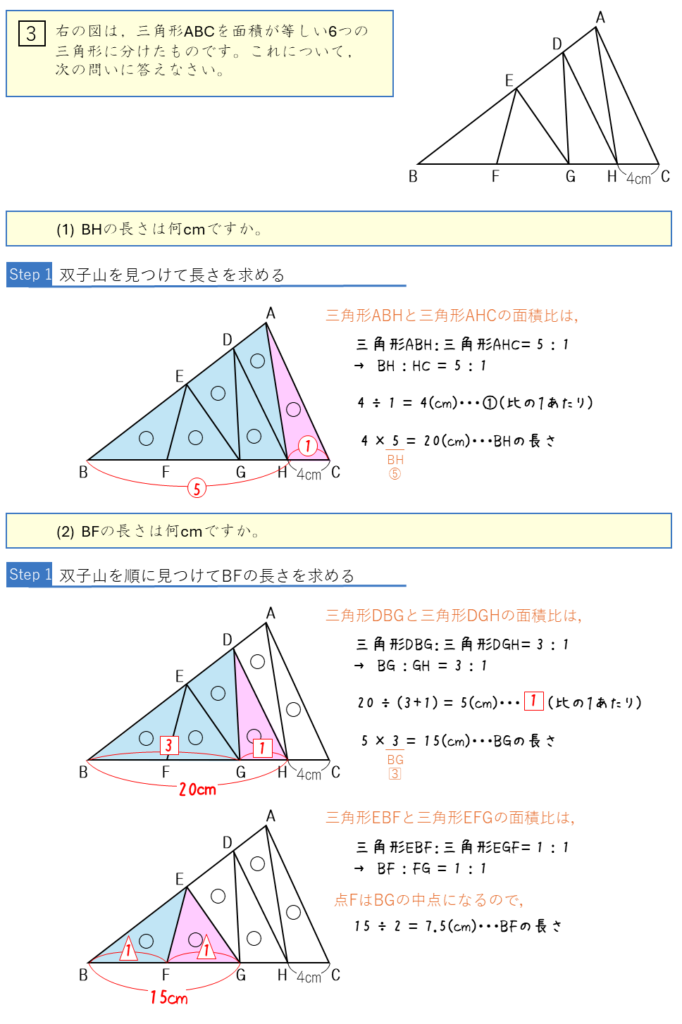
底辺の比と面積比ー3つの双子山
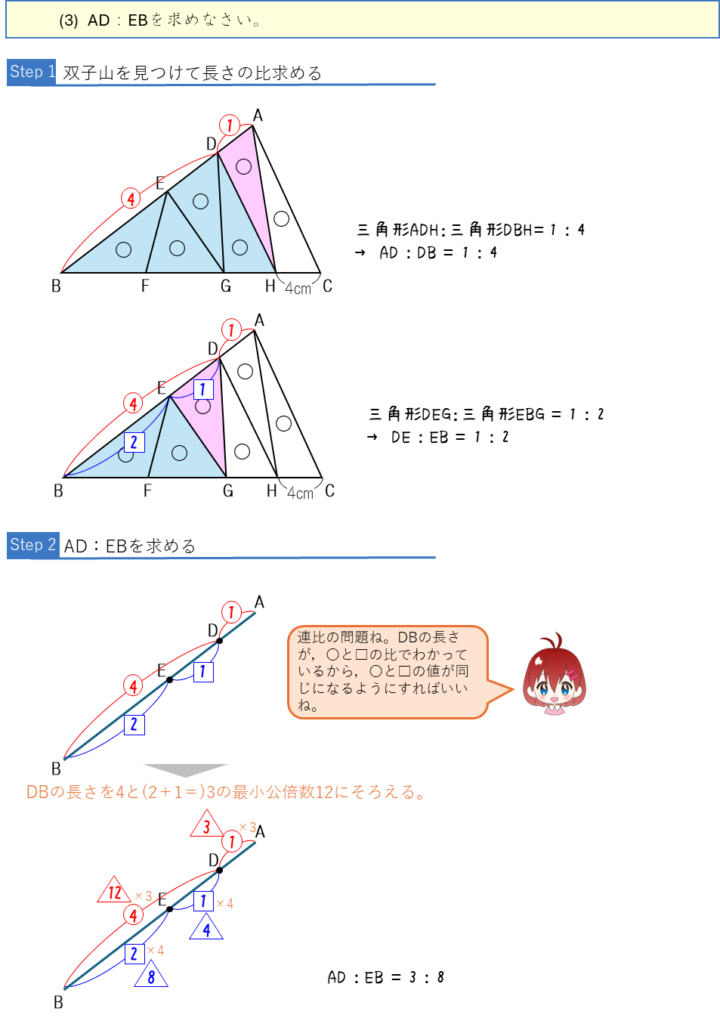
底辺の比と面積比ーたくさんの双子山と連比
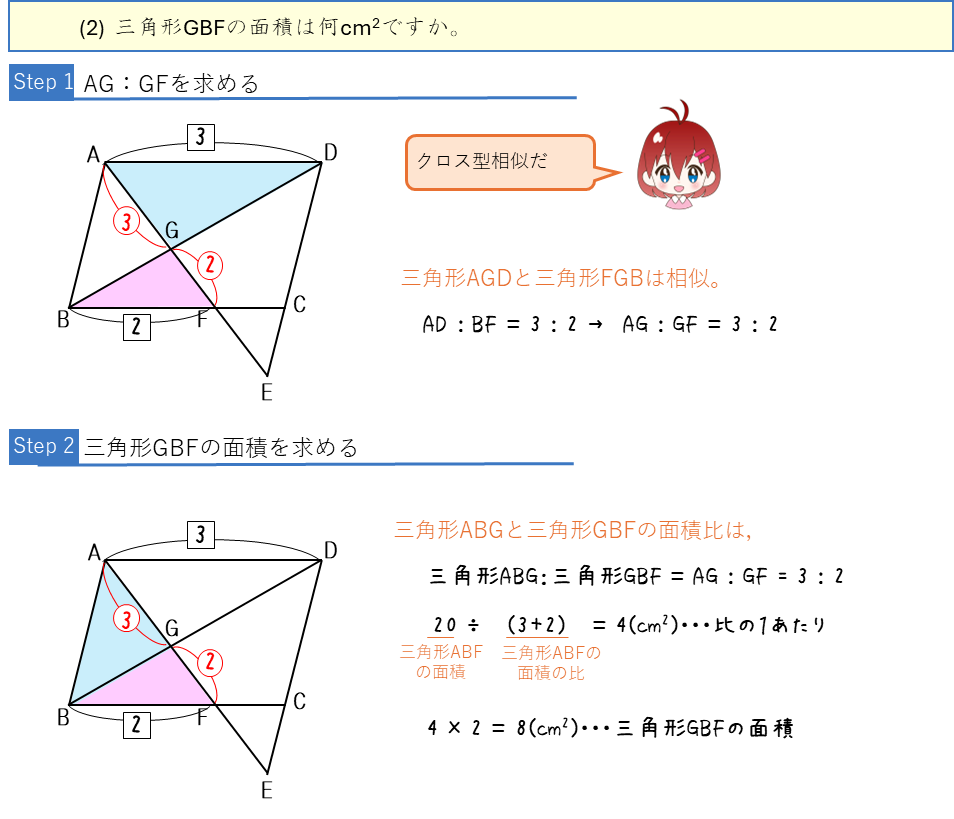
相似な三角形と高さが同じ図形の面積比


コメント
分かりやすい。基本問題や類題などの解説もやってほしいです。
コメントありがとうございます。いろいろ拡充していきたいです。どうぞよろしくお願いします。