
今回は、図形の「相似」について勉強します。相似な図形は、形は同じだけど大きさがちがう図形です。対応する辺の比が等しくなります(相似比)。特に、相似な三角形について、相似比を求めたり、その値から長さを求める問題を解いていきます。比の考えが使われるので、前回、前々回の内容も再度確認しておきましょう。
解説
三角形の相似条件
三角形の相似条件は、次の3つです。
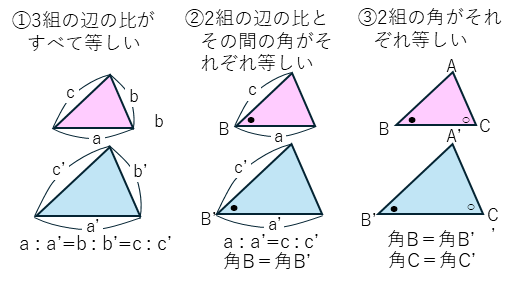
このうち、③の「2つの角度がそれぞれ等しい」ことから、相似の図形を見つけて、対応する辺の比から他の辺の長さを求める問題が多く出題されるので、よく覚えておきましょう。
三角形の相似ークロス型とピラミッド型
次の図のように、平行線があるとき、さっ角が等しい、同位角が等しいという性質から、相似な三角形ができます。
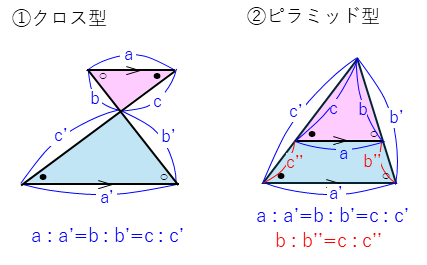
相似の問題では、「クロス型」、「ピラミッド型」の相似な三角形を見つけて解いていきます。練習問題からは、相似な三角形を2組以上の見つけるものが多くなります。
練習問題
相似な三角形の相似比
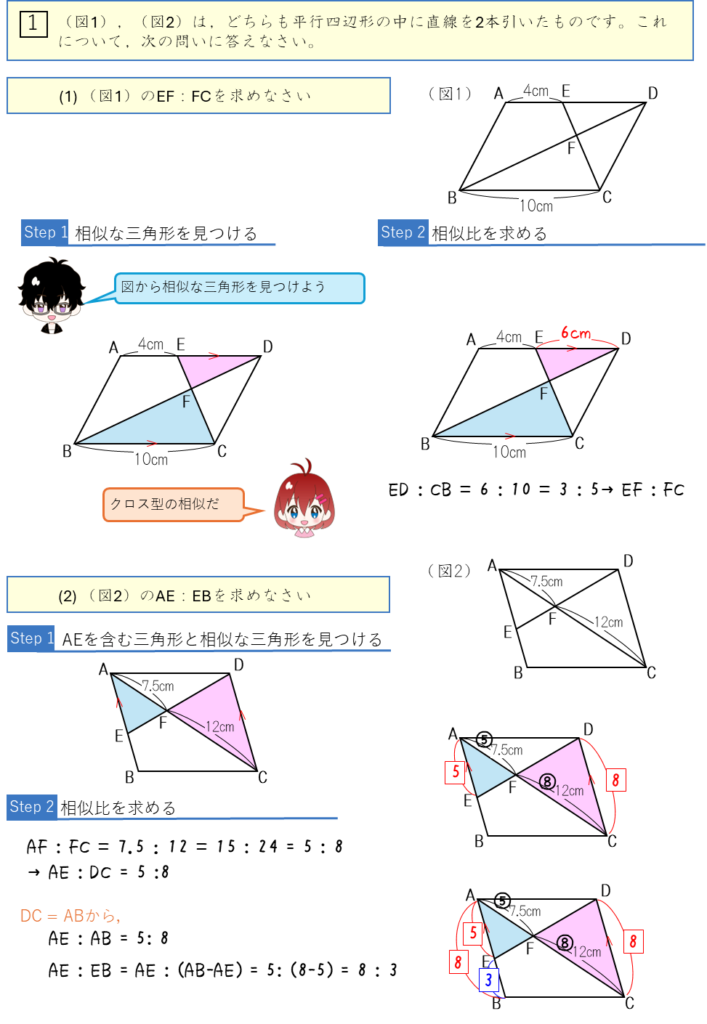
2組の相似な三角形から長さを求める
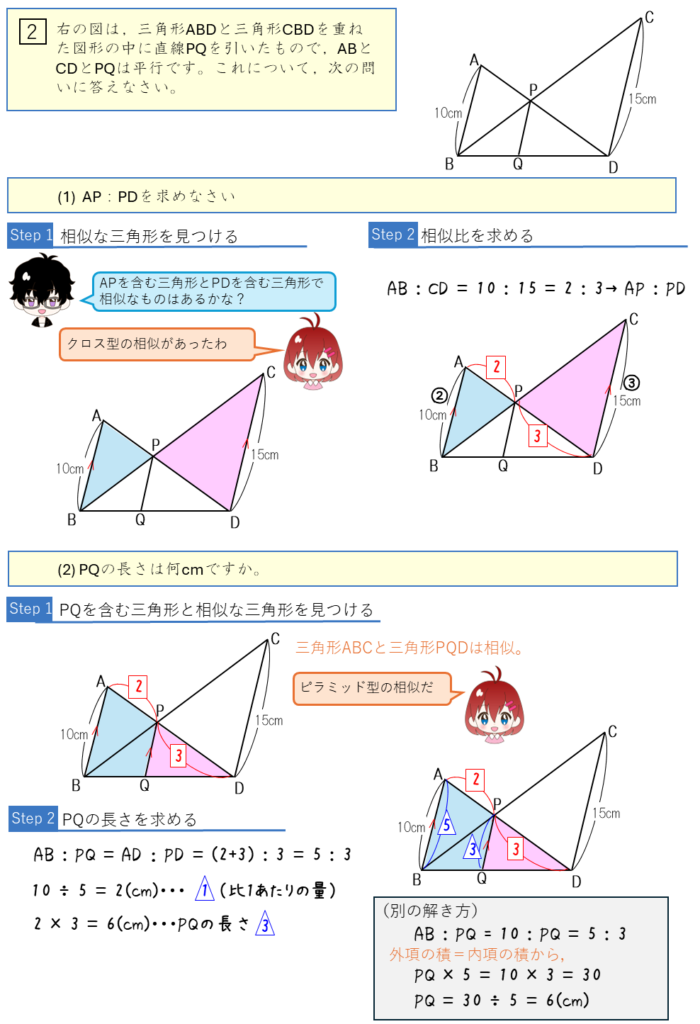
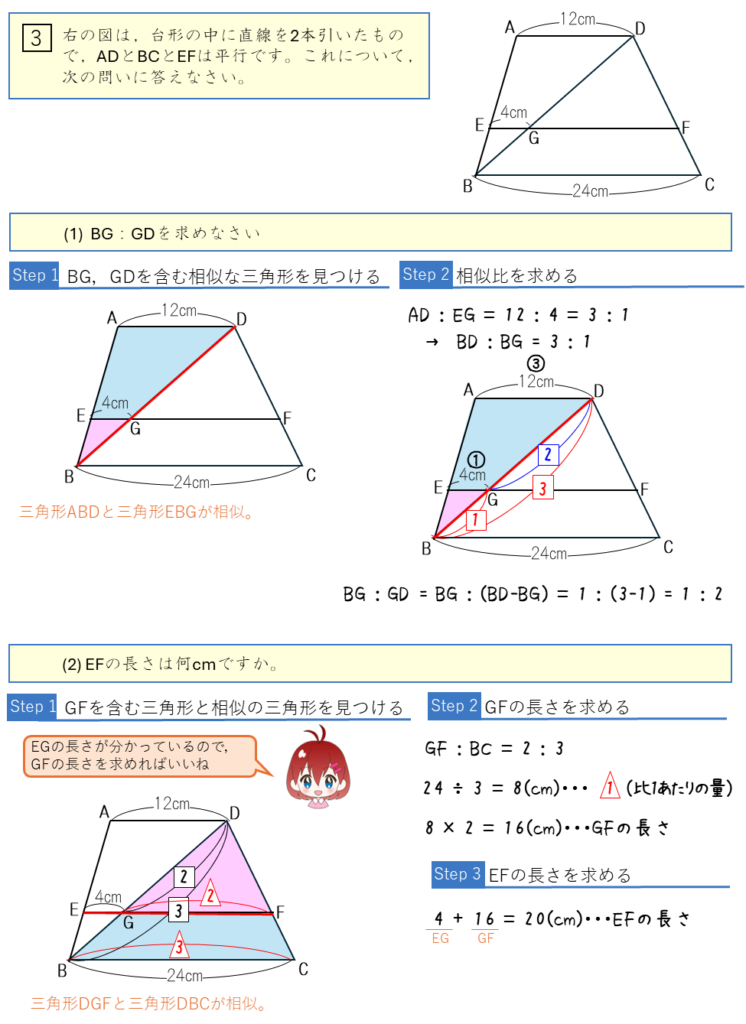
3組の相似な三角形から長さや相似比を求める
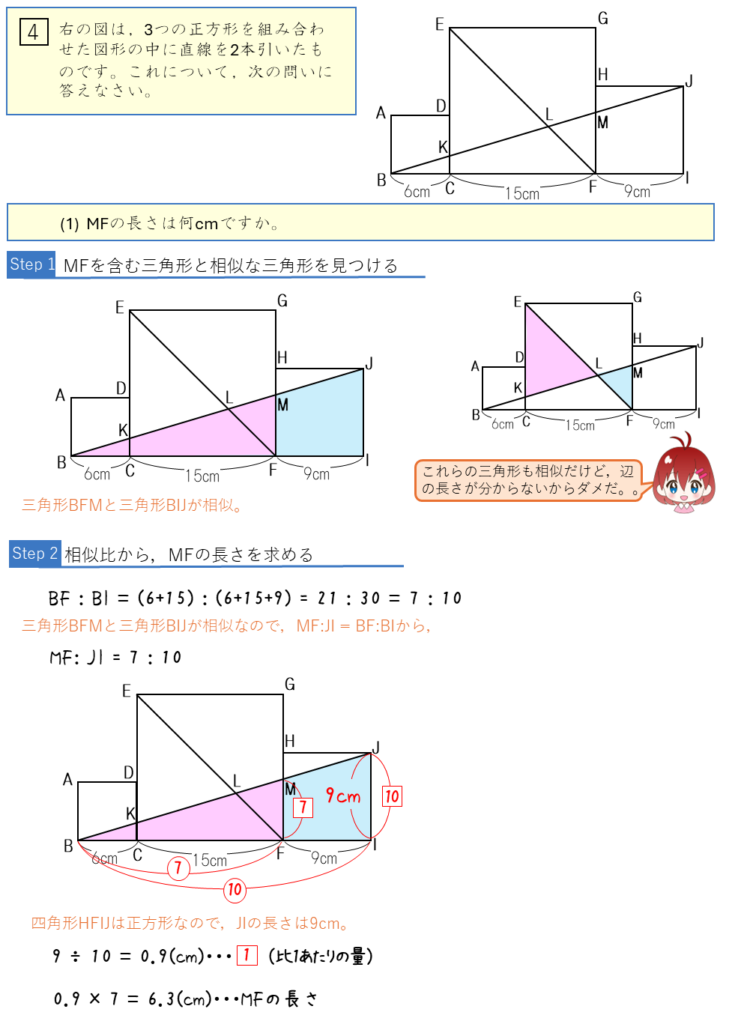
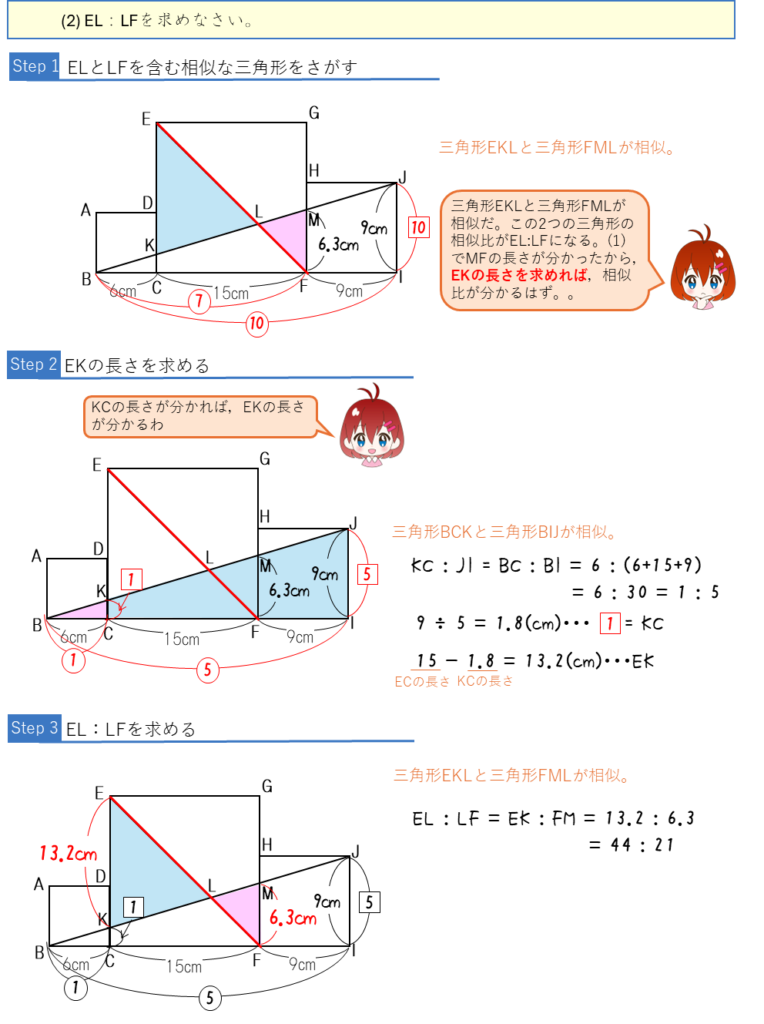

コメント