
今回は、いろいろな数列や数表の問題を勉強します。今まで学んだ等差数列(4年上第14回)、周期(4年上第13回)などの考え方を応用します。数列に慣れていないと難しいかもしれないので、基本となる等差数列や周期の考え方をしっかりと確認しながら問題にチャレンジしいきましょう。
(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説
いろいろな数列や数列を表にした数表について勉強していきます。4年のときに勉強した、等差数列(4年上第14回)や周期(4年上第13回)の考え方を使っていきますので、これらの基本が十分に理解できていないと、かなり苦戦することになります。自信がない人はしっかり復習しておきましょう。
階差数列
1, 2, 4, 7, 11,…という数列を考えてみます。数列がでたら、まず次の値と差をチェックするが基本です。

この数列では、差は一定ではなくて、1,2,3,4と等差数列になっています。このような数列を「階差数列」と呼んでいます。この数列は、
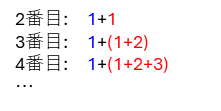
となるので、N番目の数は、「最初の数」と「等差数列の和」の合計で求めることができます。等差数列の個数は、数列の個数Nより1つ少なくなることも要チェックです。
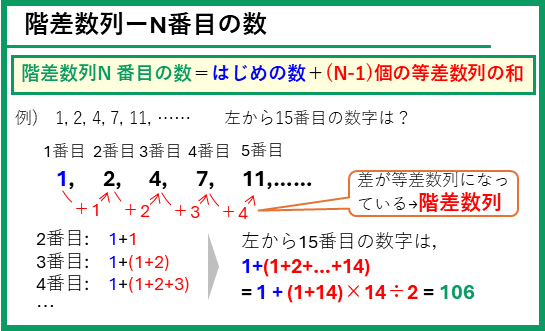
ところで、等差数列の和の求め方は大丈夫ですか? 復習のために等差数列のN番目の数と和の考え方をのせておくので確認してください。
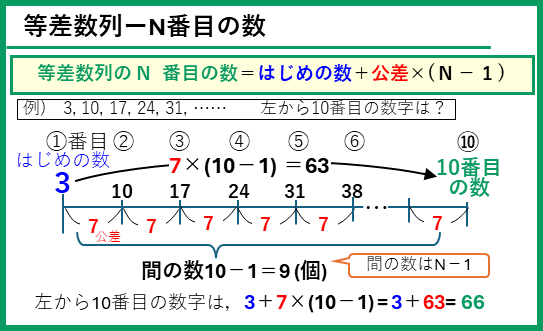
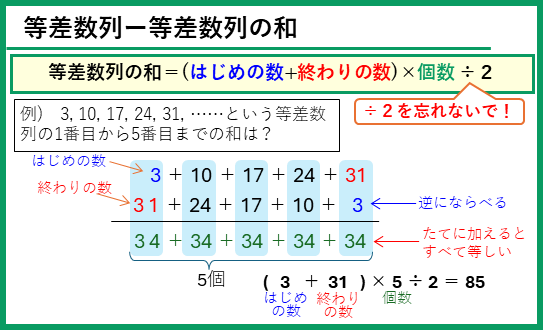
公式を丸暗記するのではなくて、等差数列のN番目の数は線分図を、等差数列の和は逆の順の数列と足し合わせることをイメージして、覚えましょう。
四角数
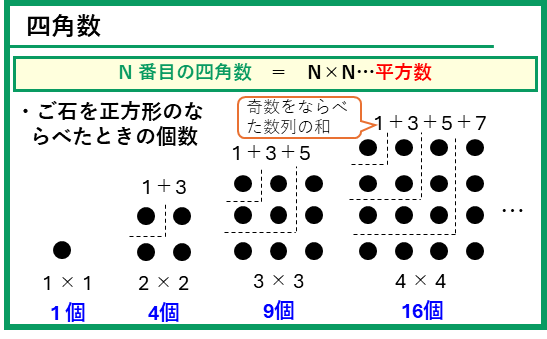
ご石を正方形にならべた個数は、1×1=1、2×2=4、3×3=9、…と同じ数をかけ合わせた数にないります。これを「四角数」と呼びます。まあ、「平方数」とも呼ぶこともあるので、両方覚えておきましょう。
この平方数は、1+3+5+7+‥‥のように、奇数をならべた数列の和になっていることも合わせて覚えておきましょう。
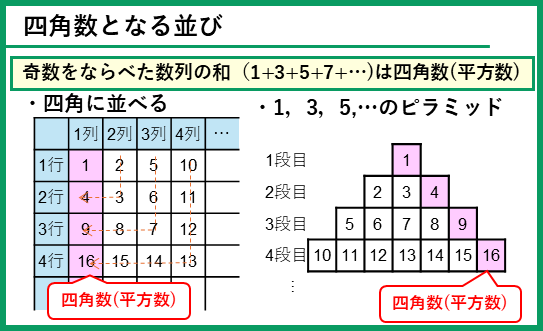
これ以外にも、四角数となるならびがあり、それが問題として出てきます。
- 正方形の形に並べる
- 1+3+5+・・・のように、奇数をならべた数列の和になる
という性質から四角数を見つけましょう。
四角数(平方数)はよく出てくる数字なのでできれば覚えておくといいです。1×1~9×9は、九九に出てくるし、10×10は100はすでに覚えていると思います。そこで、11×11~19×19の平方数について、ごろ合わせを参考にのせておきます。

三角数
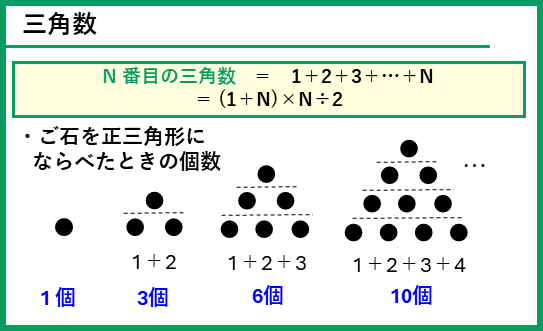
ご石を正三角形にならべた個数は、1、1+2=3、1+2+3=6、1+2+3+4=10、…と、1からの数の和になります。これを「三角数」と呼びます。N番目の三角数は、1~Nまでの数の和になるので
N 番目の三角数 = 1+2+3+…+N = (1+N) ×N÷2
となります。公式として丸暗記するではなくて、等差数列の和をイメージして解けるようにしよう。
これ以外にも、三角数となるならびとして、次のようなものがあります。
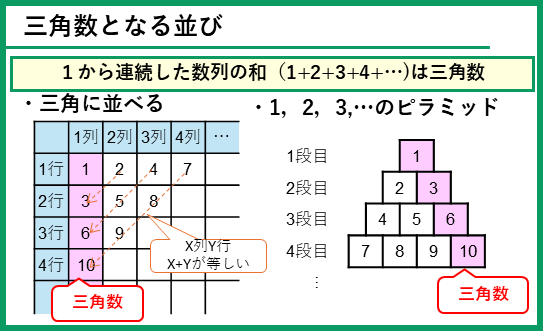
- 正三角数の形に並べる
- 1+2+3+・・・のように、1から連続した数の和になる
という性質から三角数を見つけましょう。
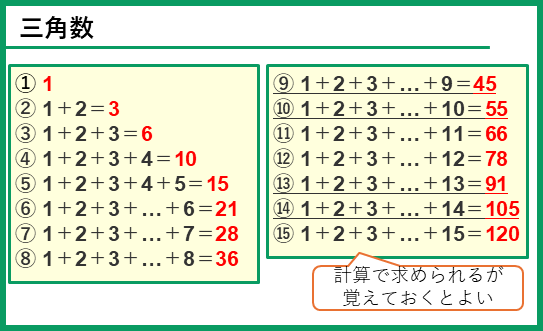
三角数は、順に数をたし合わせていくことによって求めることができるけど、覚えておくと素早く問題を解けます。15番目までの三角数をまとめておきます。全部を覚えなくても、特に50の前後や、100の前後などをおさえておくとよいです。
パスカルの三角形
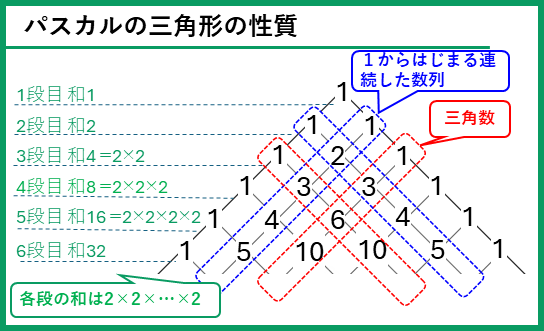
一番上と各段の両はしの数が1で、それ以外は、左上と右上の数の和となっている数のならびの三角形を「パスカルの三角形」といいます。パスカルの三角形には、いろいろな性質があります。
パスカルの三角形の性質
- 1から連続した整数の列が現れる
- 三角数の列が現れる
- 各段の和は2×2×2×…になる
なかなか面白いけど、これらの性質を使った問題は難易度が高いので要注意です。
練習問題
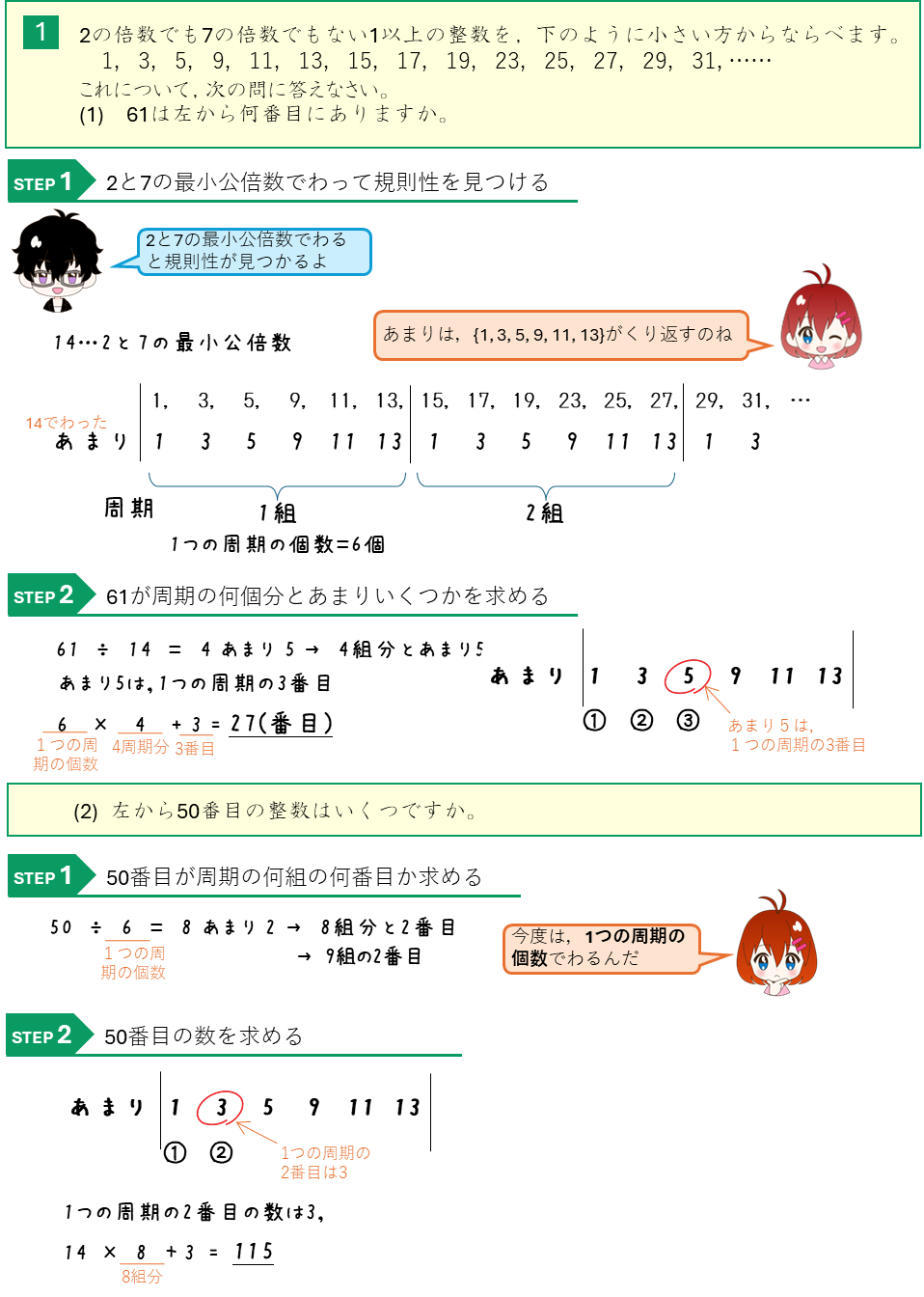
2つの数の倍数でない数列
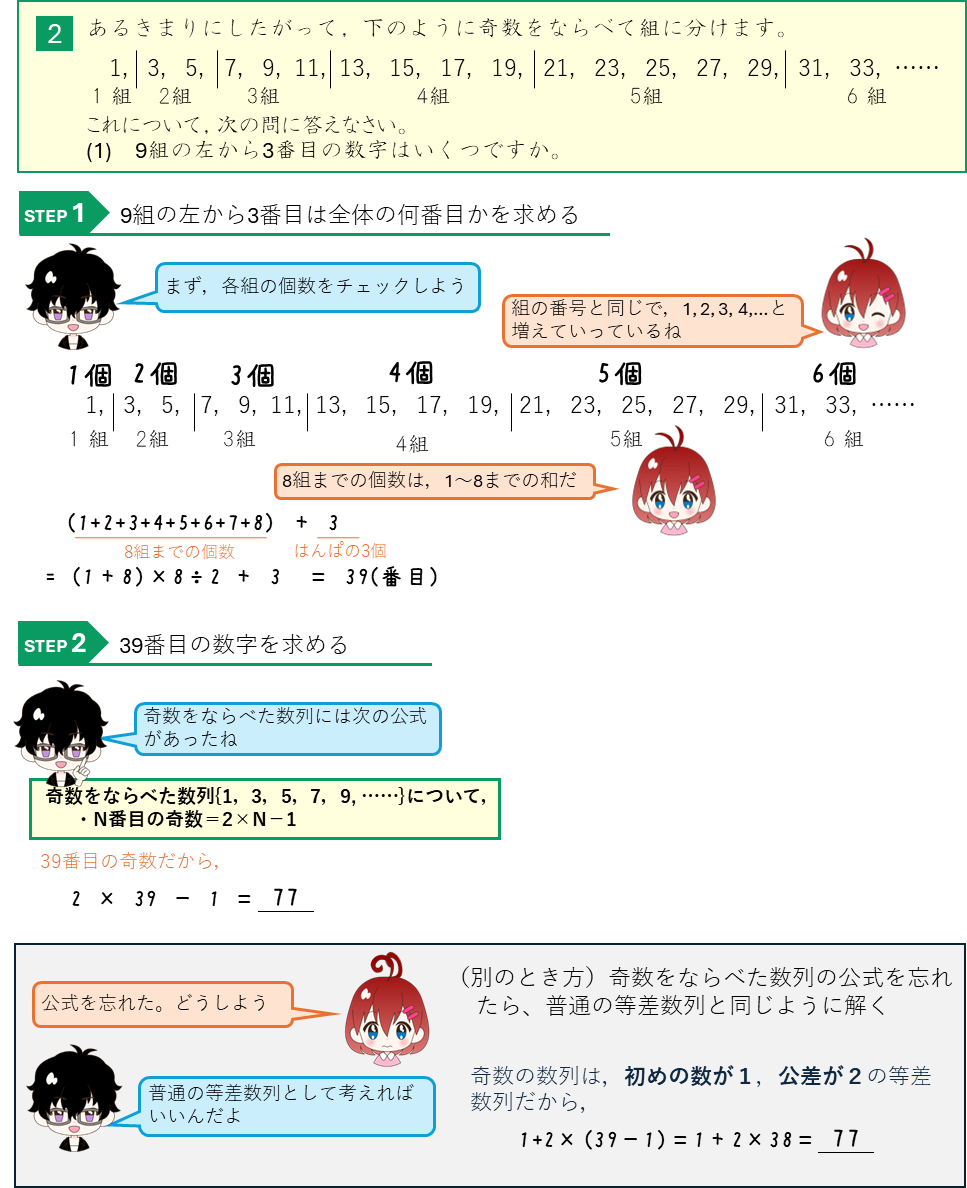
奇数がならんだ数列の組分け
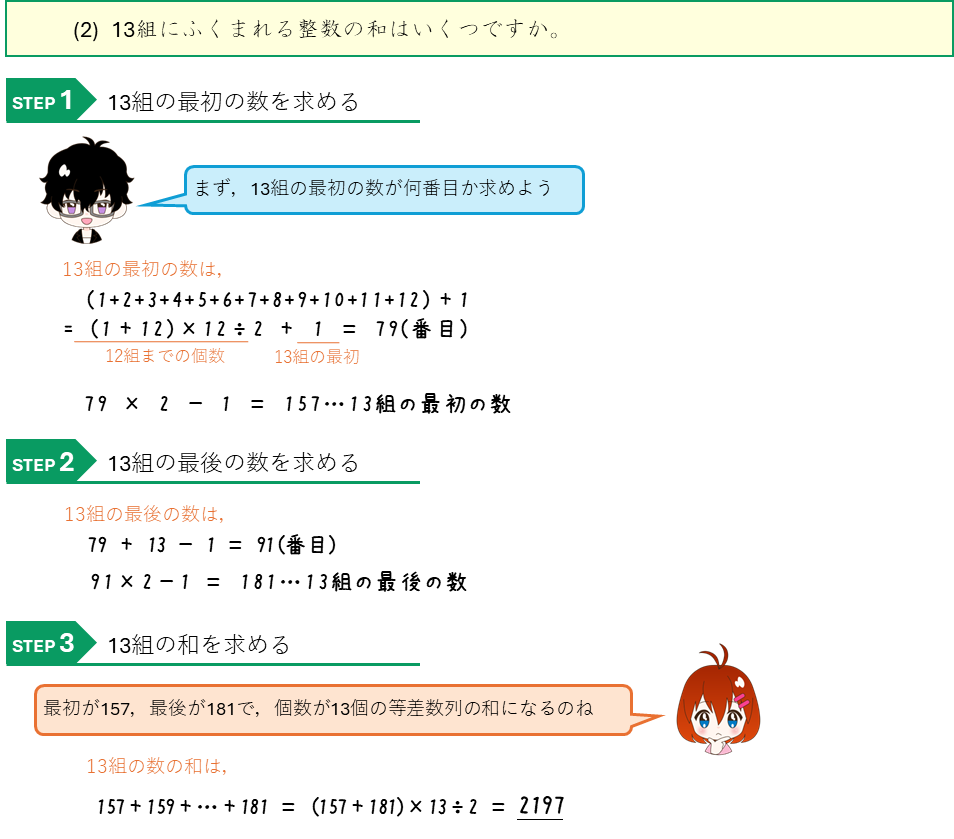
四角数の数表
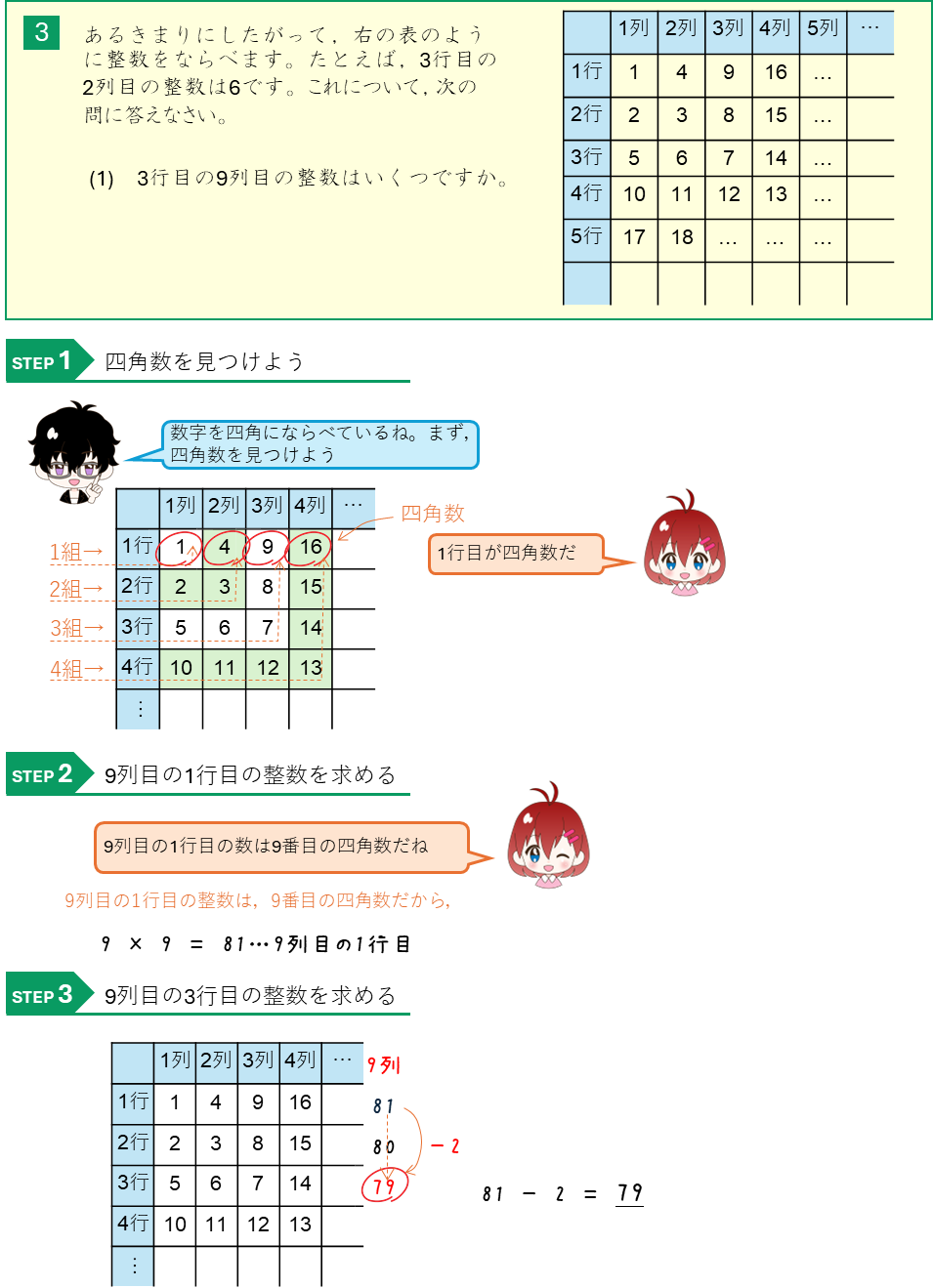
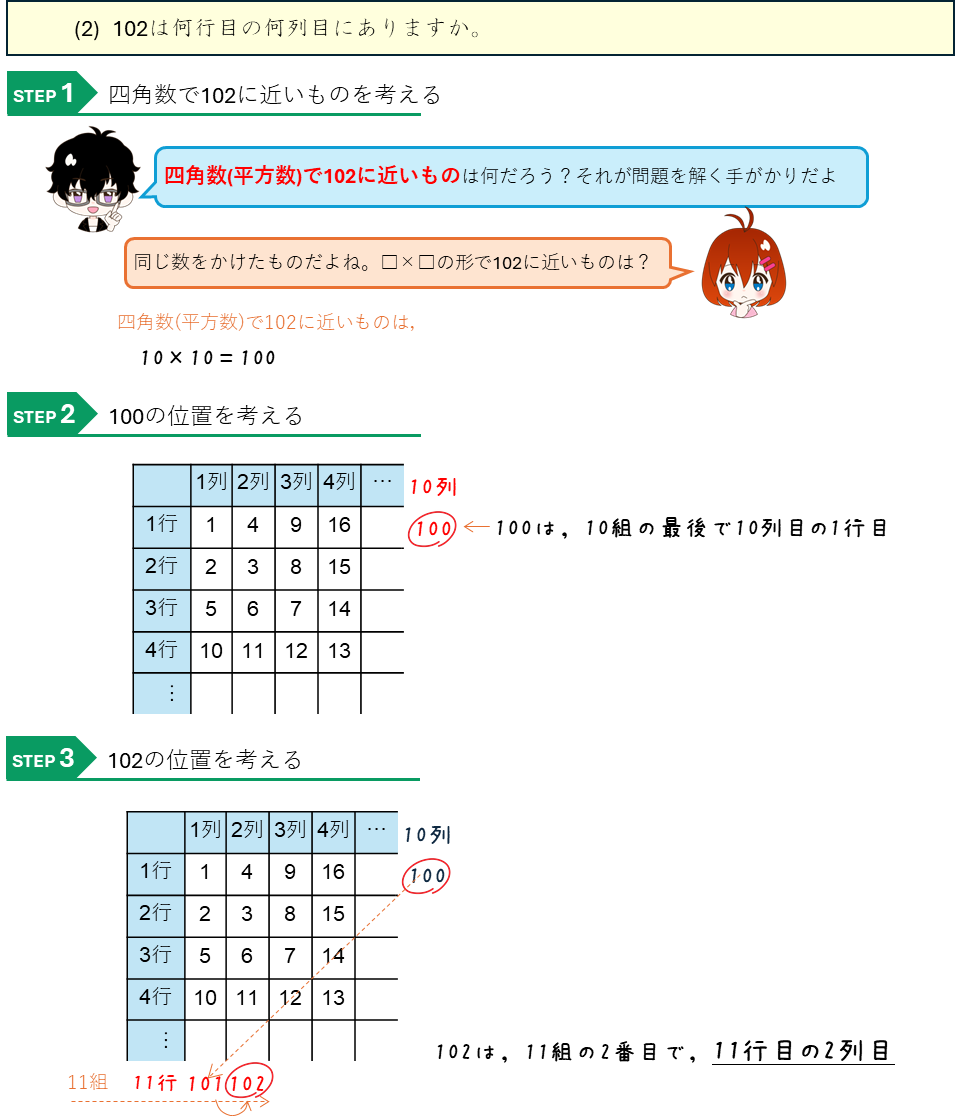
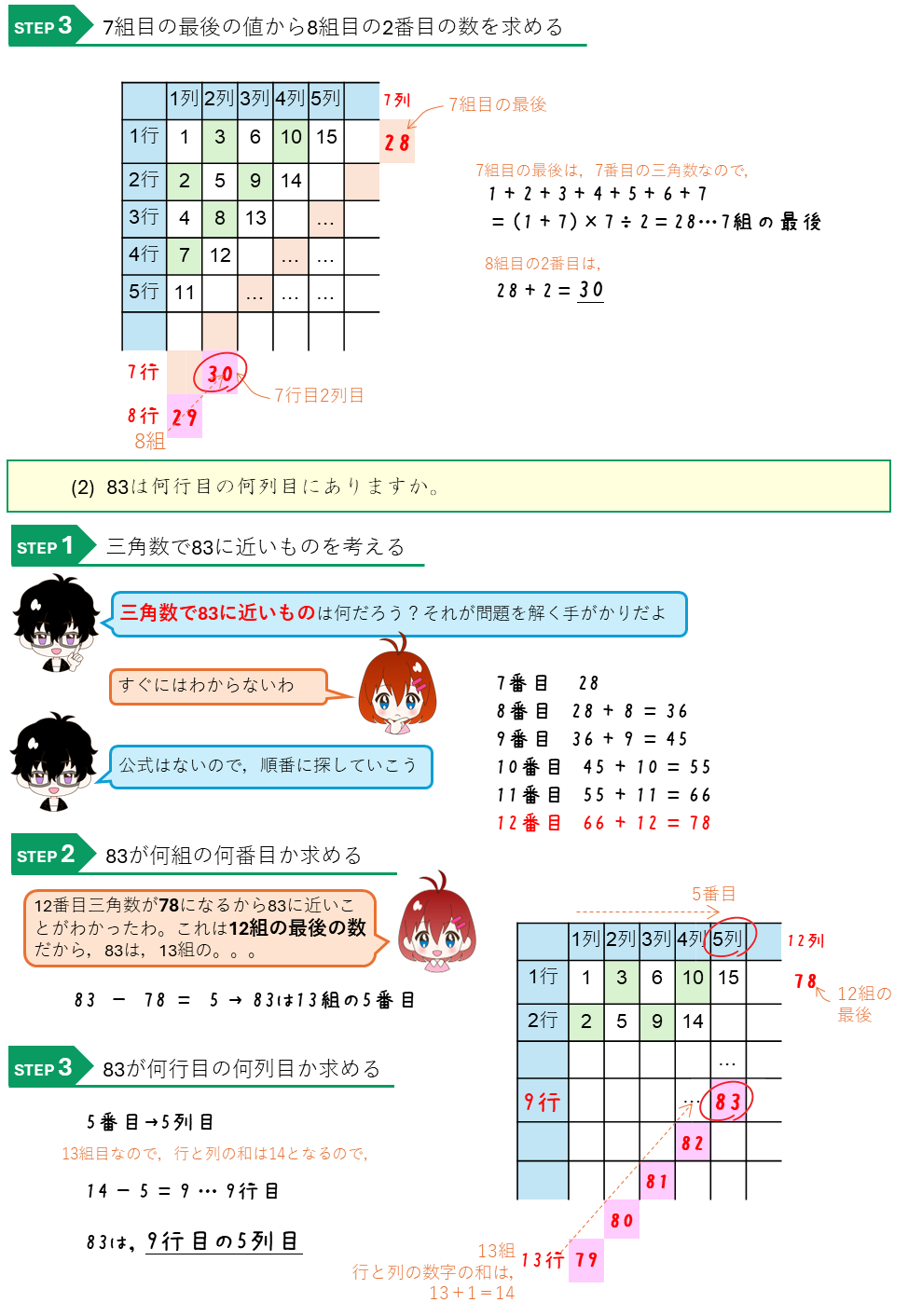
三角数の数表
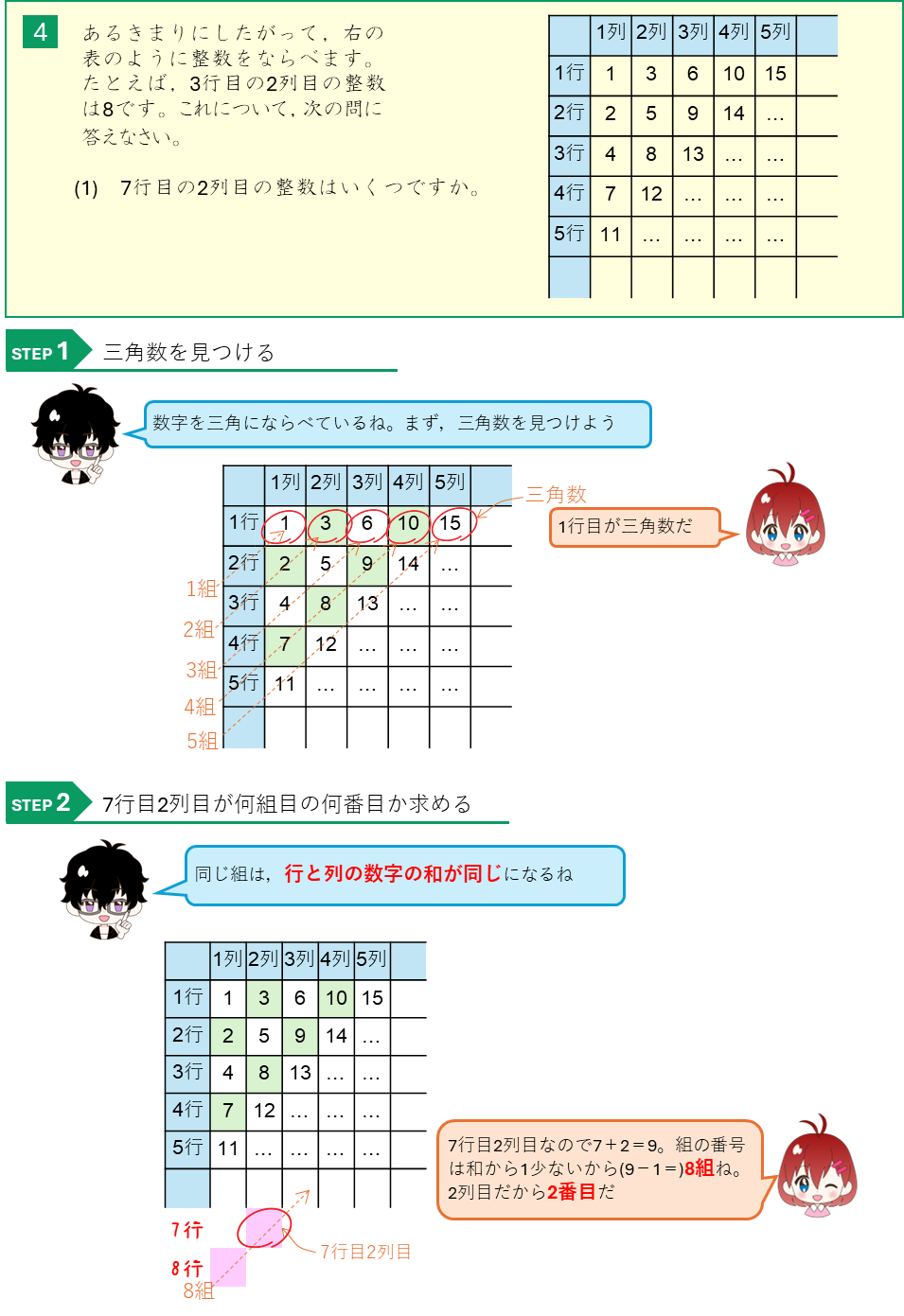
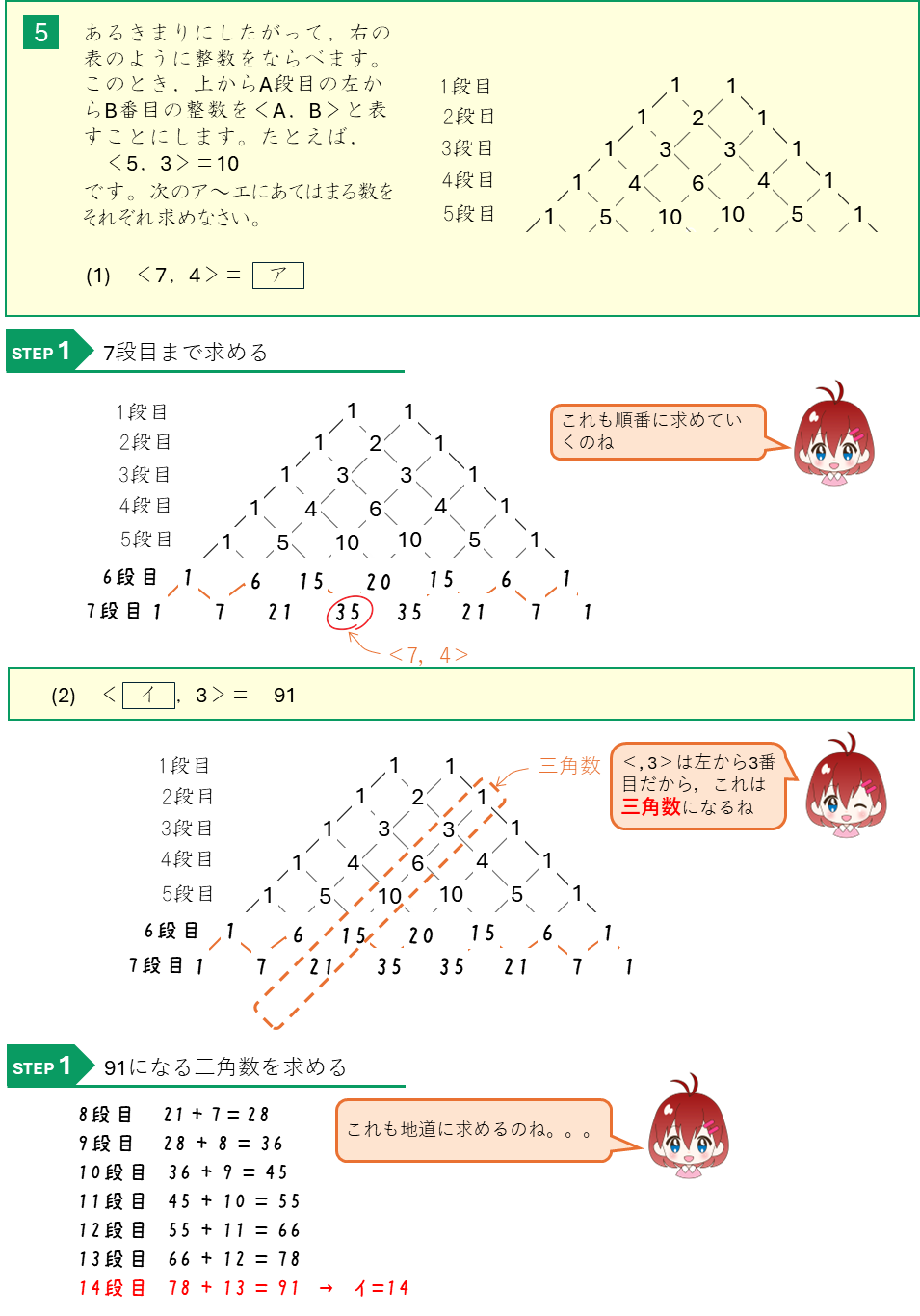
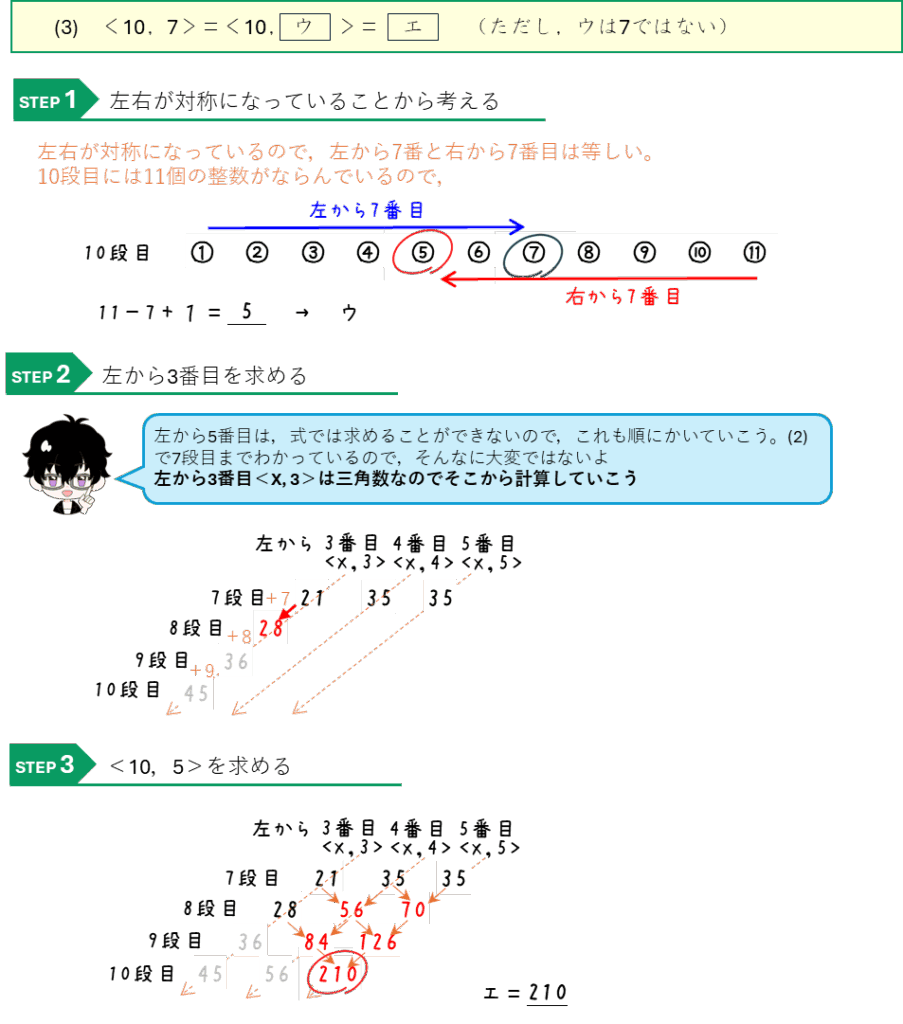
パスカルの三角形

コメント