
「面積図で解こう!」の第2回目は、つるかめ算とつるかめ算で解く問題(速さの問題、損益算(売買損益)、水量の変化、仕事算)の例題を解いていきます。
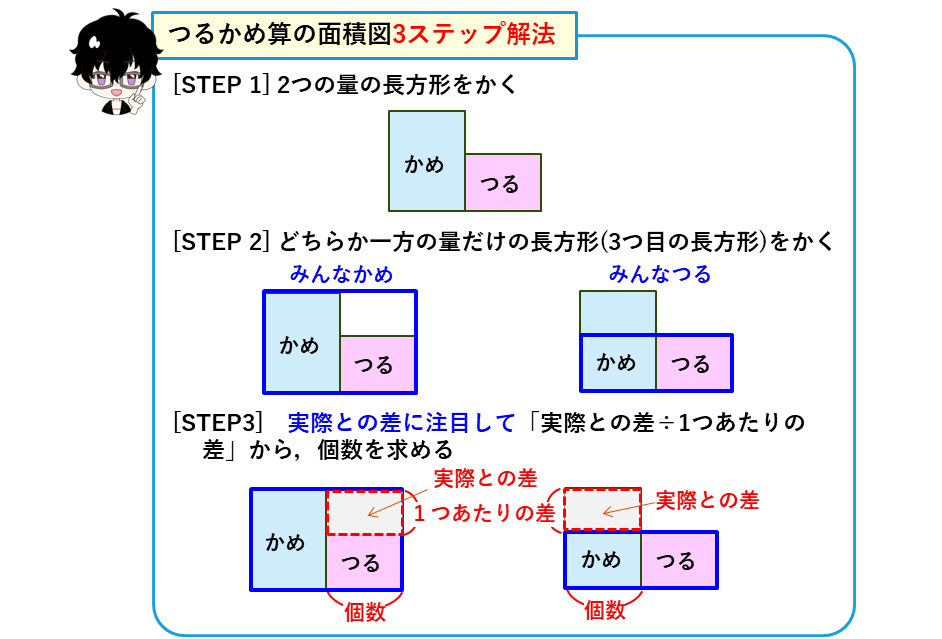
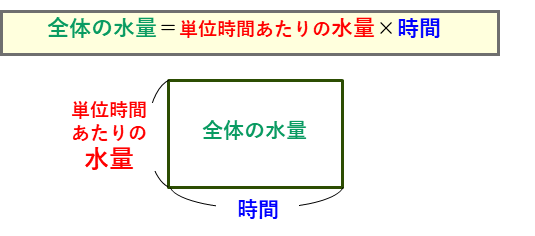
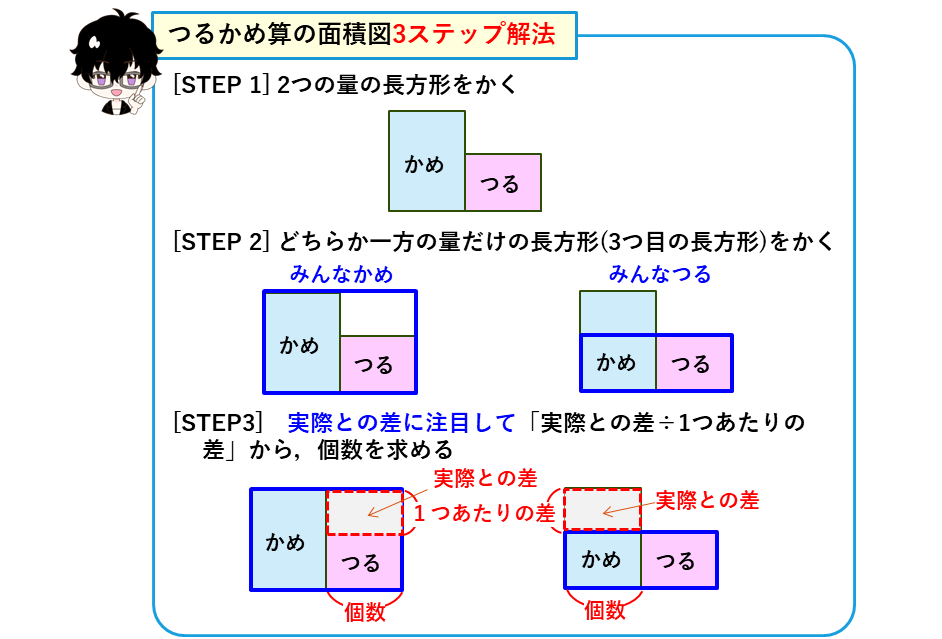
つるかめ算を面積図で解く場合は、面積で積の値を表す長方形を2個以上組み合わせて解いていきます。長方形の面積、たて、よこを計算することになり、イメージを持って問題を解くことができるようになります。まさに、面積図の本領発揮ですね。つるかめ算を面積図を使った解法は、3つの手順(ステップ)になります。3ステップ解法として覚えましょう。
つるかめ算については、四谷大塚 予習シリーズ練習問題解説(4年上 第18回 一方におきかえて解く問題)も参考にしてください。
面積図で解くーつるかめ算
つるかめ算
つるかめ算は、図表を使った解法もありますが、ここでは面積図を使った解法を解説します。

この問題には書かれていませんが、
・つるは、1羽あたりの足の数が2本
・かめは、1匹あたりの足の本数が4本
と,1つあたりの数が2種類ある問題となっています。つるとかめのそれぞれの足の数の合計は、
・つるの足の数の合計=2×つるの頭数
・かめの足の数の合計=4×かめの頭数
と2つの積の式ができるので、それぞれの長方形の面積図をかきます。

つるかめ算では、みんな”つる”、あるいは、みんな”かめ”のように、どちらか一方にみんなおきかえて解いていきます。ここでは、みんな”かめ”として考えます。(問題では”つる”が何羽か聞いているので、もう一方の”かめ”にすべておきかえます。)面積図に、みんな”かめ”だった場合の、足の合計の本数を表す3つ目の長方形をかき入れます。
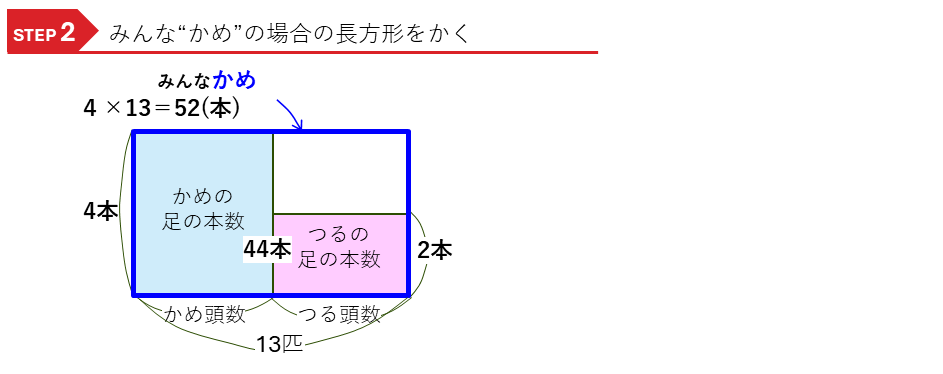
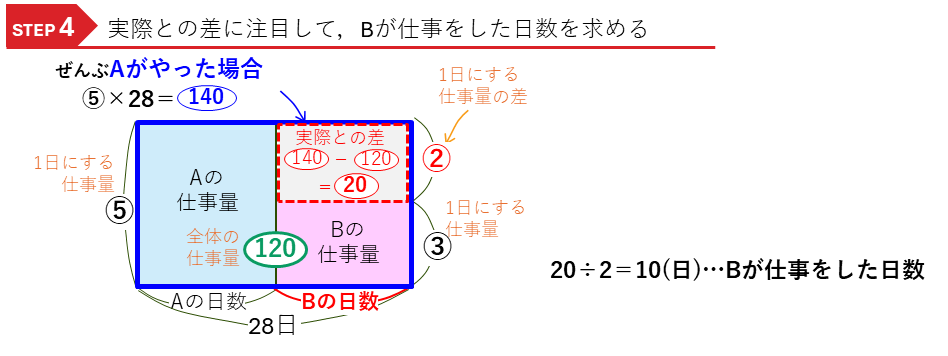
実際の足の数との差に注目します。
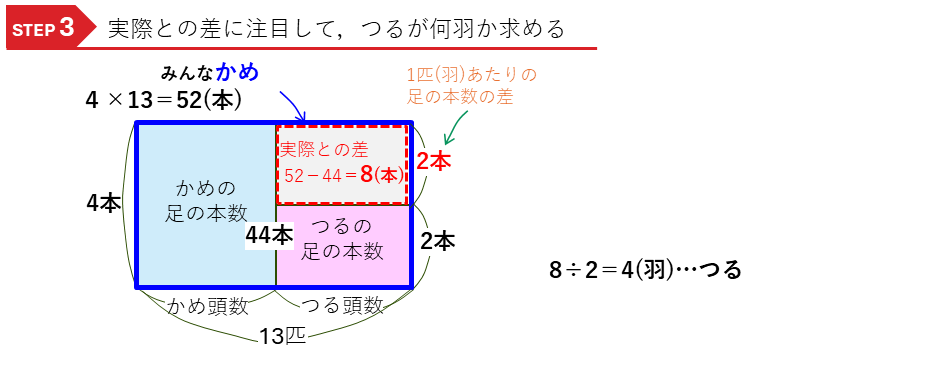
みんな”かめ”の足の合計52本に対して、実際の足の合計は44本ですので、その差の8本が面積図の赤枠の長方形の面積になります。たては一匹あたりの足の本数の差(4-2=)2本なので、つるの頭数は、
8÷2=4(羽)…つるの頭数
で求めることができます。
つるかめ算の面積図3ステップ解法
上で説明した通り、つるかめ算は面積図を使って3つのステップ解くことができます。この3ステップ解法をまとめておきます。
つるかめ算の面積図の弱点ー弁償のつるかめ算(弁償算)には使えない
面積図でつるかめ算を解くのは、とても分かりやすいのですが。この面積図には弱点があります。弁償のつるかめ算には使えません。

弁償のつるかめ算は、次のような問題です。

この問題も、
お皿を洗ったアルバイト代の合計=20円×洗ったまい数
弁償する代金の合計=50円×わったまい数
という2つの積の式ができ、すべて一方にした場合を考えて解いていきます。しかし、ここではお金をもらうとお金をしはらうという、プラスとマイナスになっています。これが面積図の解法ではうまく図にかけません。
この問題では、図表(おだんご図)を使った解法を使います。(詳しい解説は、四谷大塚 予習シリーズ練習問題解説(4年上 第18回 一方におきかえて解く問題)を読んでください。)

お皿をわったときに、わらなかったときもらえる20円をもらえないだけでなくて、50円はらわないといけないので、その差が20+50=70円になります。このプラスとマイナスの差を、図表で表現できるので問題を解くことができます。
では、次から、つるかめ算を使った特殊算などの問題を解説します。つるかめ算と本質的に同じ問題になっているので、面積図で解けることを確認しましょう。
面積図で解くーつるかめ算の仲間たち
速さのつるかめ算ー途中で速さが変わる
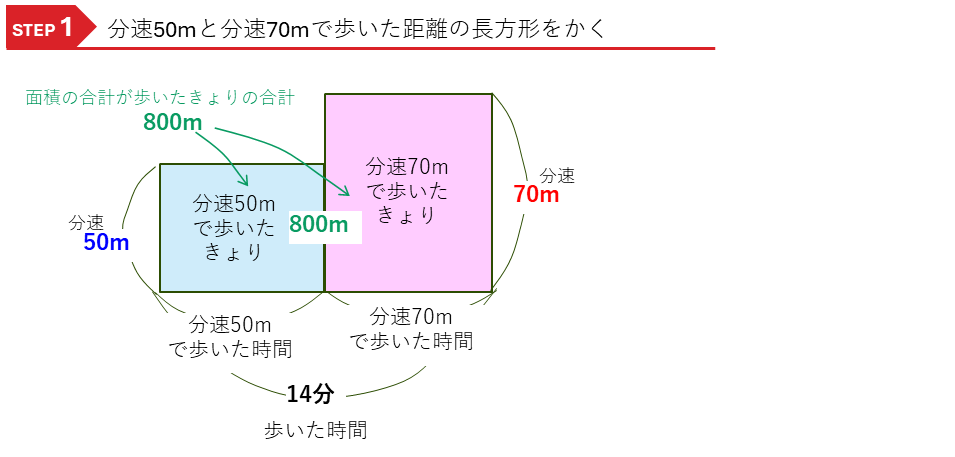
途中で速さが変わる問題です。

・はじめは分速50m
・途中からは分速70m
と,1つあたり(1分あたり)の数が2種類ある問題となっており、つるかめ算と同じです。
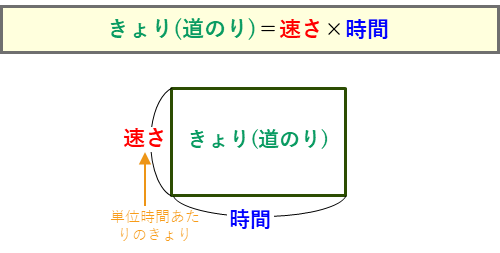
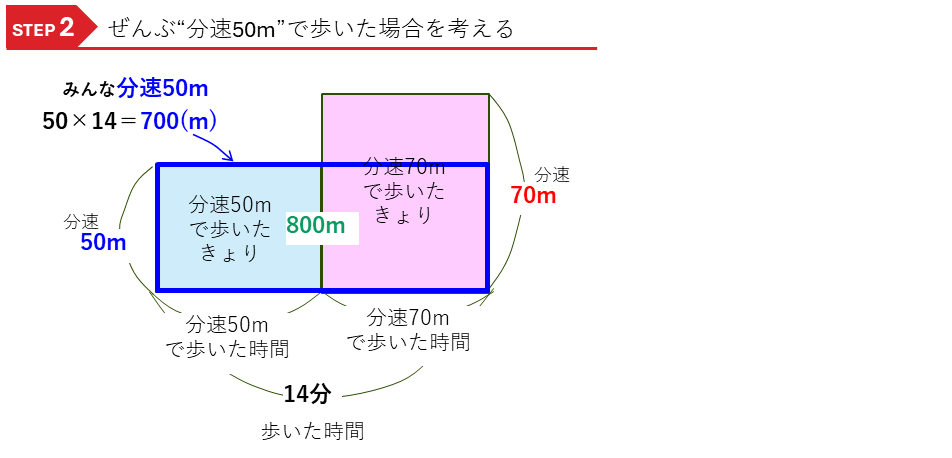
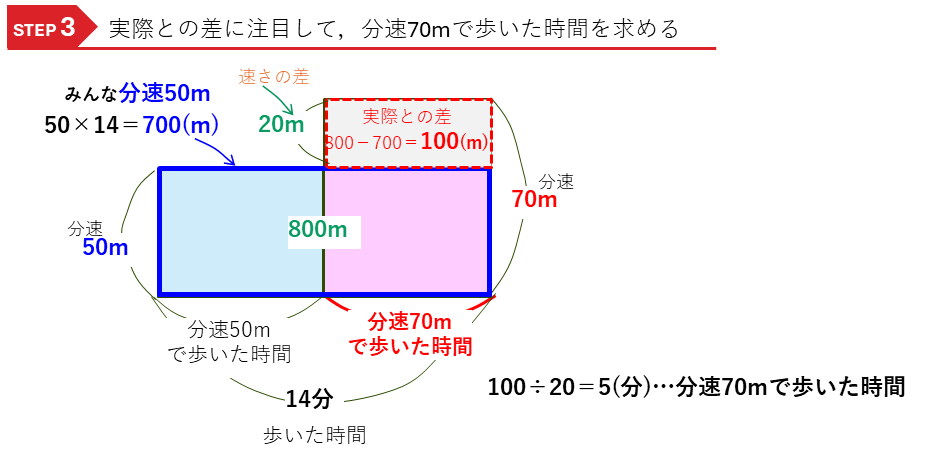
・分速50mで歩いた距離(m)=50(m)×分速50mで歩いた時間(分)
・分速70mで歩いた距離(m)=70(m)×分速70mで歩いた時間(分)
と2つの積の式ができるので、それぞれ速さの公式の長方形の面積図をかきます。
つるかめ算で解く損益算(売買損益)ー1日目と2日目で売値が変わる
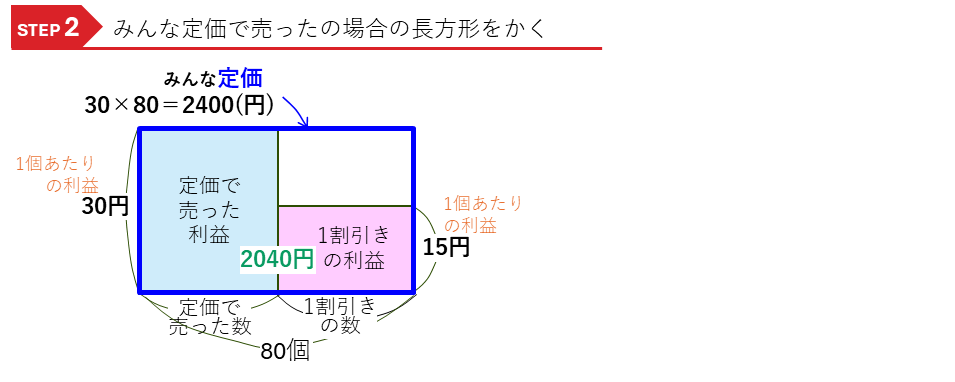
売値が変わる損益算の問題です。

・1日目は、仕入れ値の2割5分の利益を見込んだ定価
・2日目は、定価の1割引き
と,1つあたりの数が2種類ある問題です。
・1日目の利益(円)=定価の1個あたりの利益×定価で売った個数
・2日目の利益(円)=定価の1割引きの1個あたりの利益×2日目に売った個数
という2つの積の式ができるので、1日目の定価で売った利益、2日目の定価の1割引きで売った利益を求めて、それぞれの長方形の面積図をかき、解いていきます。


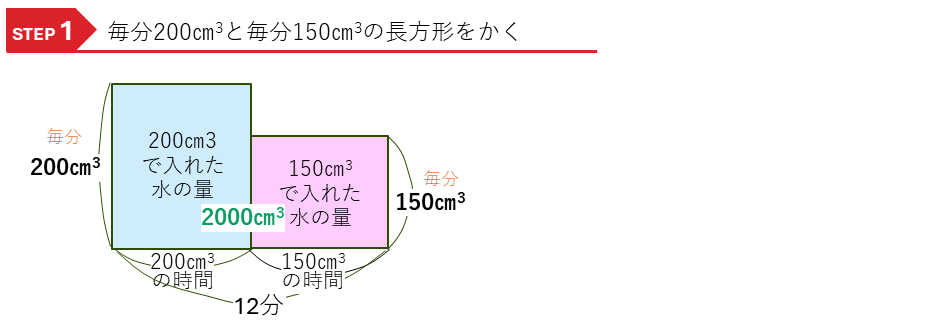
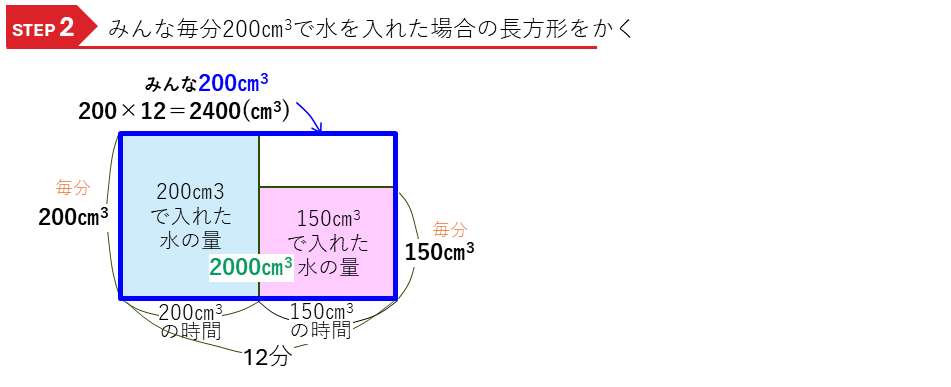
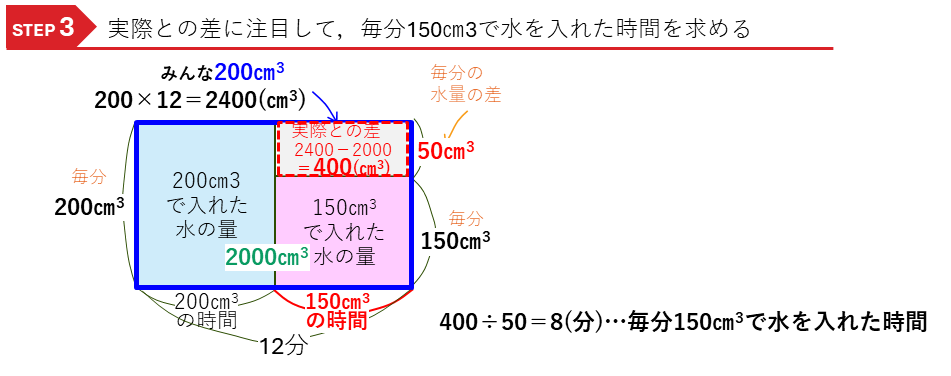
水量変化のつるかめ算ー途中で水量が変わる
途中で水量が変わる問題です。

・毎分200㎝3
・毎分150㎝3
と,1つ(1分)あたりの数が2種類ある問題です。
・毎分200㎝3で入れた水の量(㎝3) = 200(㎝3) × 毎分200㎝3で入れた時間(分)
・毎分200㎝3で入れた水の量(㎝3) = 200(㎝3) × 毎分200㎝3で入れた時間(分)
という2つの積の式ができるので、それぞれ水量変化の長方形の面積図をかき、解いていきます。
つるかめ算で解く仕事算ー途中で1日にする仕事量が変わる
途中で1日あたりの仕事量が変わる仕事算です。

この問題は、途中でAからBに人が変わることで、1日にする仕事量が変わっています。問題には直接、1日にする仕事量が書いていません。 問題には、
A1人ですると24日かかり,B1人ですると40日かかります。
とあり、ここから、AとBの1日にする仕事量と、全体の仕事量の比を求めて解いていきます。このステップが加わるので、この問題はつるかめ算の3ステップ解法+1の4ステップになります。

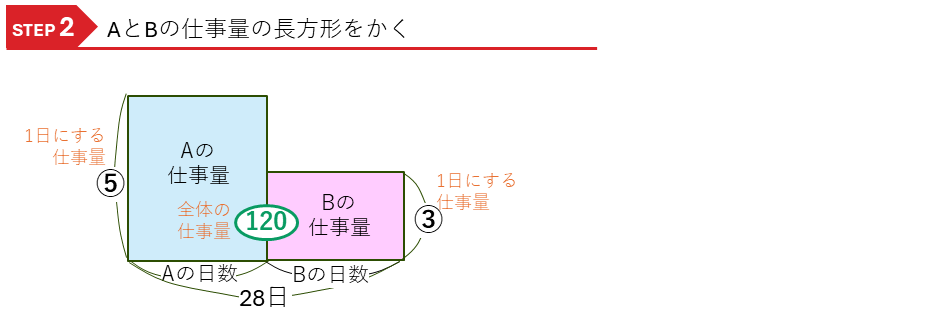
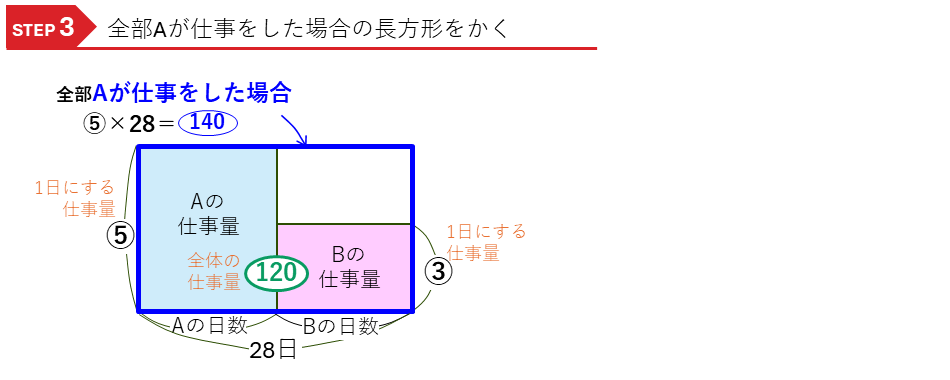
これで、この問題は、全体の仕事量が(120)で、
・Aが1日でする仕事量⑤
・Bが1日にする仕事量③
と,1つ(1日)あたりの数が2種類ある問題で、
・Aがした仕事量 =Aが1日でする仕事量 ×Aが仕事をした日数(日)
・Bがした仕事量 =Bが1日でする仕事量 ×Bが仕事をした日数(日)
という2つの積の式ができ、それぞれの長方形の面積図をかき、解くことができます。

つるかめ算の面積図まとめ
つるかめ算とその仲間たちの線分図での解法について解説してきました。これらの問題はみんな、
・1つあたりの数が2種類ある問題
です。その仲間たちの速さのつるかめ算、損益算、水量変化のつるかめ算、仕事算では、それぞれ、速さ、売値、水量、仕事量が、途中で変わる問題です。つるかめ算の応用はよく出題されます。1つあたりの数が途中でかわるなどして2種類以上ある問題に注意しましょう。
解法は、3つの手順(ステップ)になるので、「つるかめ算の面積図3ステップ解法」として覚えましょう。
コメント