
場合の数は,苦手な人はとことん苦手。まったくお手上げという人もいるかもしれないね。今回は、なんで苦手になってしまうか、その理由をあげて対策を考えてみよう。場合の数は、中学受験だけでなくて,中学,高校でも習うし、さらに,就職活動の適性検査でも出題されるんだ。ここでちゃんと理解しておくといこう。
「場合の数」が苦手な理由は?
場合の数が苦手な理由を、リストアップしてみると、
<本当の基本レベル>
- 和の法則と積の法則がごっちゃになる
- 樹形図をかいているところで,抜けやダブりのミスがでる
- 場合の数の公式を使えない
<基本レベル>
- いろいろな種類の問題があって混乱する
<応用レベル>
- 条件付き問題が解けない
まずは、基本レベルまでの対策を考えていこう。
本当の基礎レベルでのつまづきと対策
■和の法則と積の法則がごっちゃになる

和の法則と積の法則はちゃんと理解しているかな?

場合の数を足す場合と、かける場合があるんだよね
Aの場合がa通り、Bの場合がb通りあるとき、
✓ Aの場合、または、Bの場合は何通り?→ 別々に起こるので足し算のa+b通り(和の法則)
✓ Aの場合のぞれぞれで、Bの場合が起こるときは何通り?→同時に起こるのでかけ算のa×b通り(積の法則)
になるよ。
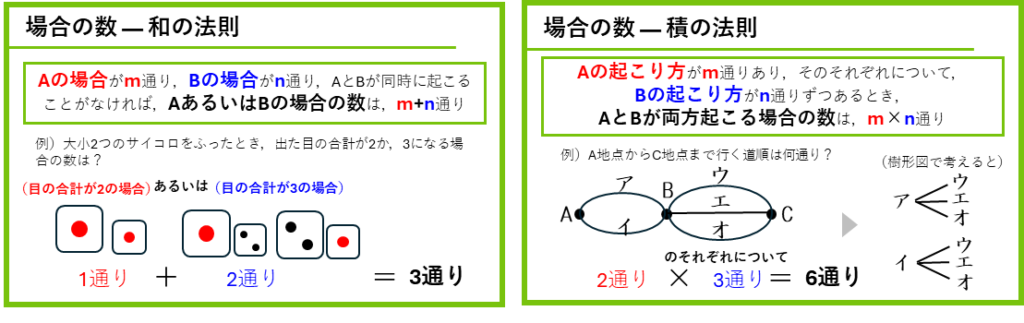
ならび方の公式や組み合わせ方の公式では、積の法則が使われています。応用問題などで場合わけを行ったときは、それぞれの場合の数を合計するので和の法則が使われることになります。場合の数をとくためには、和の法則と積の法則の考えがしみついている必要があります。
■樹形図でかいているところで,抜けやダブりのミスがでる
樹形図をかくときは、
- 小さい順,ABC順などきまりをつけてならべる
- 組み合わせでは、逆の順番はかかない
- 小さい順では、2の後に1はかかない、3の後に2,1は書かない
- ABC順では、BのにはAをかかない,Cの後にはA,Bはかかない ようにする

樹形図のポイントをカードにまとめたので参考にしてね
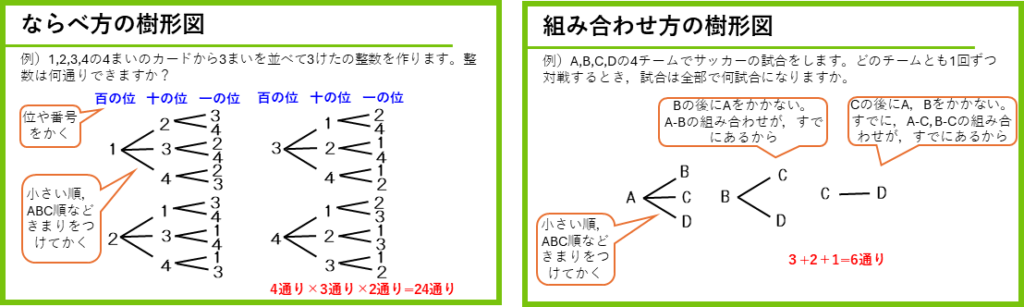
■場合の数の公式をうまく使えない

樹形図をかくのは大変だよね。樹形図をかいていると、規則性があることがわかるよね

4枚のカードで3けたの整数を作る場合、1のカードが6通りだと、ほかの2、3、4も6通りだったわ
ならべ方では、樹形図と公式を対応させて理解していきましょう。
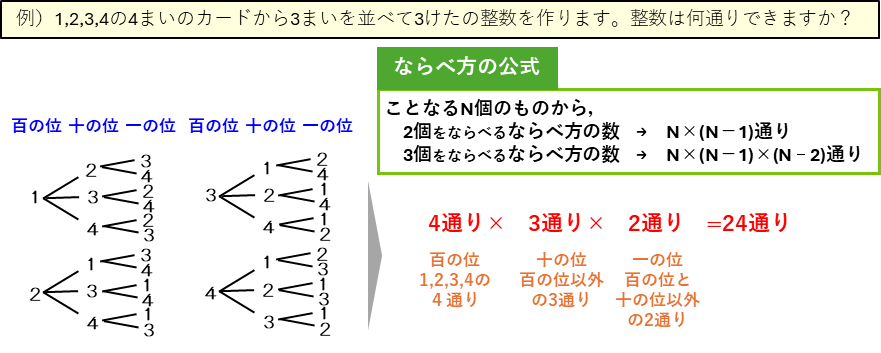
組み合わせ方では、ならべ方の公式で求めたならべ方の数を、2個を選ぶときは2個のならび方(AとBであれば、A-BとB-A)が1つとして考えるので÷2、3個を選ぶときは3個のならび方(3x2x1の6通り)を1つとするので÷6をする。このことを理解したら、2個はならべ方の数÷2、3個はならべ方の数÷6と覚えてしまおう。

場合の数の公式のカードだよ

基本レベルでのつまづき

場合の数のとき方は、今説明してきた「本当の基本レベル」で説明した。樹形図、ならべ方の公式、組み合わせ方の公式、和の法則、積の法則になる。それぞれが難しいわけではないけど、使いこなせるようになるのが重要だよ。場合の数は、基本レベルの問題でもいろんな問題があるんだ。その種類が多すぎるのでわけが分からなくなってしまうかもしれない。
ここで、場合の数の問題を整理して、とき方をまとめていくよ。
■いろいろな種類の問題があって混乱する
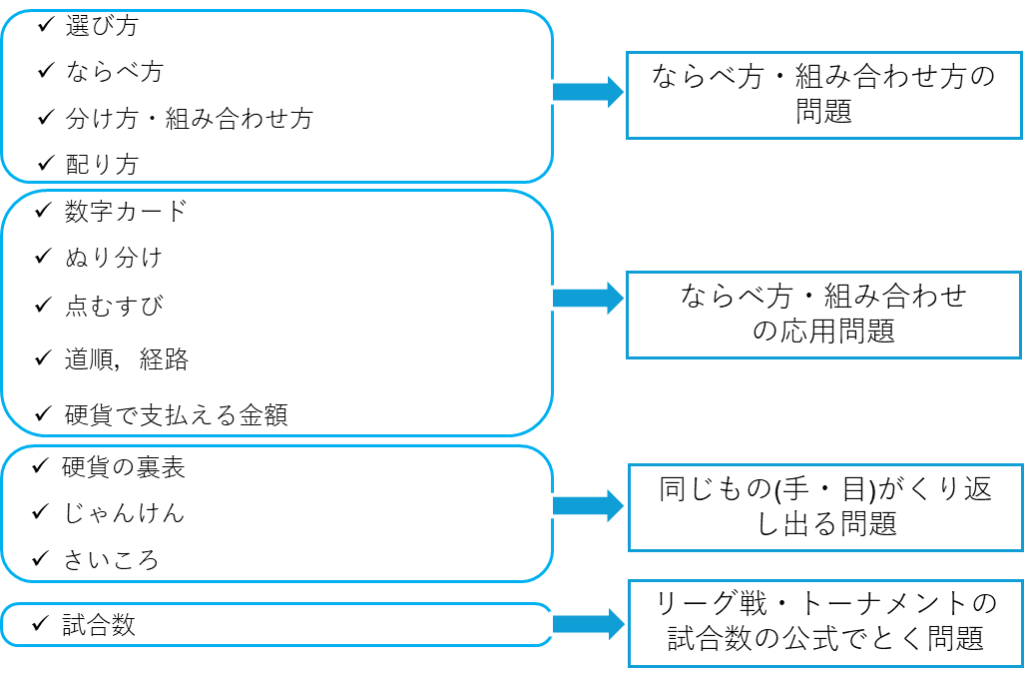
場合の数の問題を整理すると、以下のように12種類くらいあります。
- 選び方
- ならべ方
- 分け方・組み合わせ方
- 配り方
- 数字カード
- ぬり分け
- 点むすび
- 道順,経路
- 硬貨の裏表
- じゃんけん
- さいころ
- 硬貨で支払える金額
- 試合数
- ・・・・
基本問題レベルでもこんなに多くの種類の問題があるため、場合の数をよく理解していないと、どうやってといていくのか迷ってしまうかもしれません。場合の数が苦手である一番の理由はここにありそうです。たくさん種類があるだけでなくて,似ているけど、とき方が違うもののあって、基本レベルの問題でも難易度が高いです。ここでは、問題を以下のグループに分けて、攻略方法をまとめていきます。まずは、選ぶ・ならべる・分ける・配るという問題を整理してみます。
ならべ方・組み合わせ方の問題
選び方、ならべ方、分け方・組み合わせ方、配り方についての問題です。
- 選ぶ:委員長を選ぶ,リレー選手を選ぶ,係を選ぶ,グループのメンバーを選ぶ
- ならべる:リレーの順番を決める,カードをならべる,ご石をならべる
- 分ける:部屋分けする,グループに分ける
- 配る:お菓子を配る
など、いろいろなケースの問題があってとまどってしまうね。ここでは、問題を5つに分類してそれぞれのとき方を整理していきます。
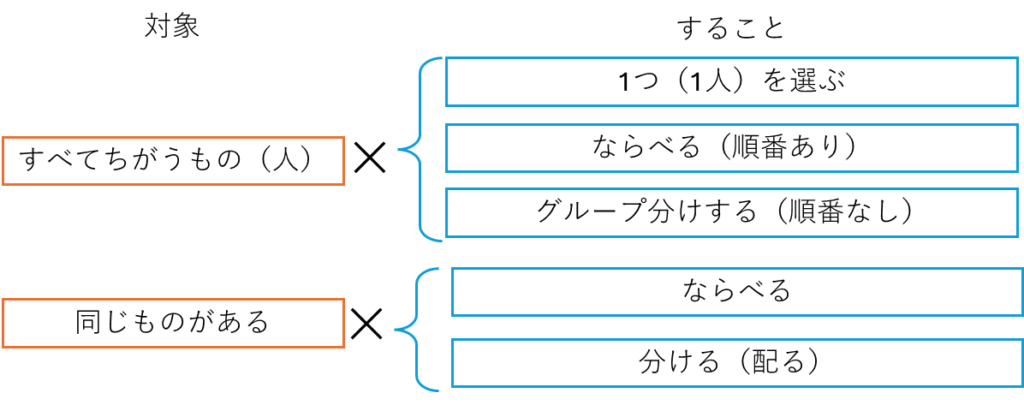
問題を「対象」が何かと。「すること」に分けてみます。一つ目は、選ぶ、ならべる、グループ分けするなどの「対象」が、それぞれすべてちがうもの(人)なのか、同じものがあるのかで問題のとき方が変わります。もう一つは「すること」です。1つだけを選ぶのか、順にならべたり、それぞれちがうことに選んだりするのか、あるいは、グループ分けするのか(選んだ中で順番はない)、という点を問題を読んで区別する必要があります。
①ちがうもの(人)から1つ(1人)を選ぶ


この問題では、「対象」はA,B,CとD,Eなので、みんなちがっている


この問題も、「対象」はA,B,C,D,Eでみんなちがう
②ちがうもの(人)をならべる(順番あり)


ならべ方の公式が使える問題ね

この2つの例題は、対象はA,B,C,D,Eとはすべてちがうものである。また,ならぶ位置や走る順番もそれぞれちがっていることを確認します。「ちがうもの(人)をちがうところに(順に)ならべる」問題であり,ならべ方の公式でとくことができます。
③ちがうもの(人)をグループ分けする(順番なし)

3人の図書委員の中には順序はないわ。組み合わせの問題ね


これらの問題では、対象となるA,B,C,D(,E)はそれぞれちがっています。一方で,図書委員,そうじ係のメンバーには順番はなく,グループのメンバーを選ぶ「グループ分け」の問題であり,組み合わせ方の公式でとくことができます。
④2種類以上の同じものを並べる


この問題では、「対象」は黒玉と白玉の2種類で、それぞれ2個以上ある。今までの「対象」がみんなちがっていた問題とは異なるね

左からならべていく考え方だとうまくいかない。。。


組み合わせ方の問題になるなんて、発想の転換が必要だ
⑤同じものを分ける(配る)


同じものを、みんなで分ける問題ね
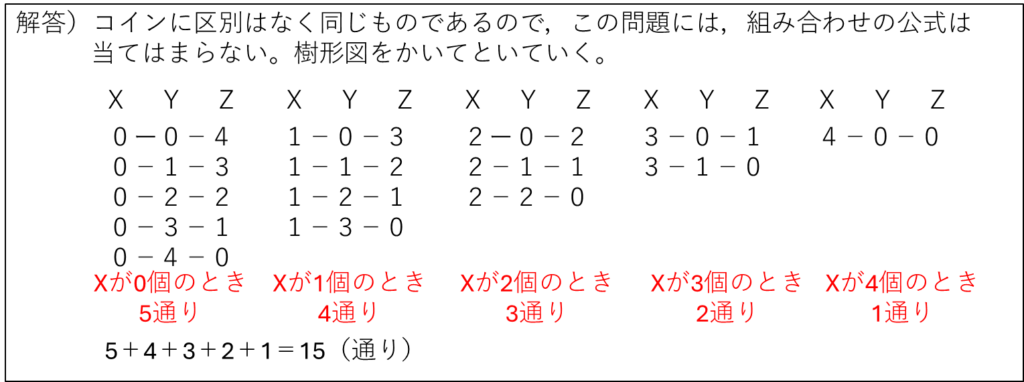
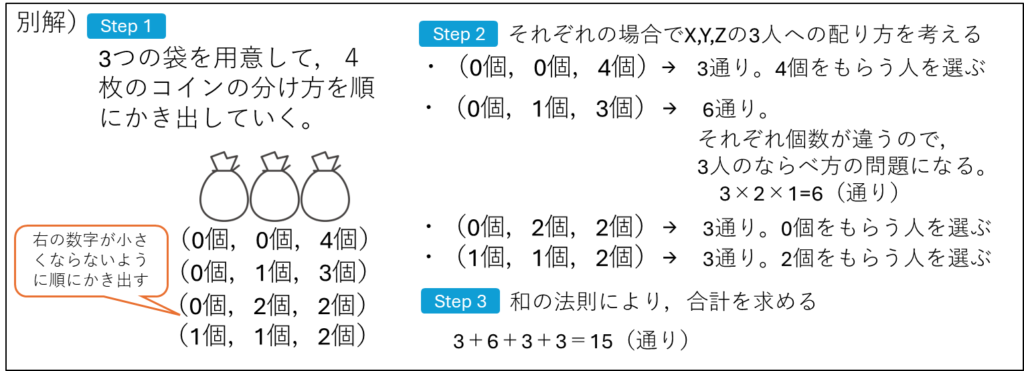
この問題は、ある数をいくつかの数の和に分解してといていくので「和分解」と呼ばれます。分解したそれぞれの場合が何通りあるか求めます。
ほかにも,「サイコロを2回振って,出た目の和が6になる目の出方」などの問題があります。

同じものを分ける問題では、みんなに分ける個数をかき出すのね
ならべ方・組み合わせ方の問題の5分類まとめ

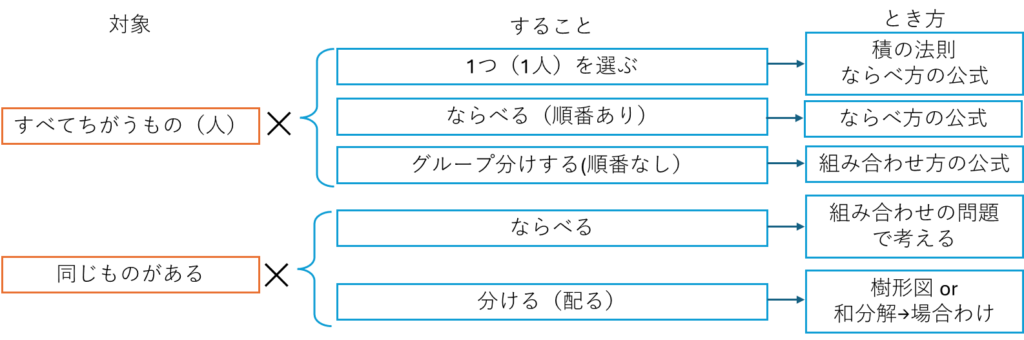
さいごに、ならべ方と組み合わせ方を5つに分類して、そのとき方をまとめておきます。ならべる・組み合わせる対象が、すべてちがうものなのか,同じものなのか,順にならべるのか,グループに分けるだけかによって,とき方が変わったね。問題文をよく読んで,区別できるようになろう。

コメント