
素数は、約数が1とその数自身の2個しかない(1より大きい)整数(1は素数にふくまない)です。つまり、他の数で割り切れない特別な数字です。
素数については,古代ギリシャの時代から多くの数学者によって研究されてきましたが,まだ解決されていない問題がたくさんあります。素数の表れ方に規則性があるのかどうかについても、いまだに解明されていません。
中学受験での素数は,約数や倍数を求めるため素因数分解で使ったり,分数の約分でわる数にしたりするだけでなく,中学受験では素数の性質を使った問題が出題されることがあります。
日能研シカクいアタマを丸くする(2023年10月) https://www.nichinoken.co.jp/shikakumaru/202310_sa
中学受験プロ講師ぶろぐ(2021年3月11日) https://www.chugakujuken.com/koushi_blog/kawakami/20210311.html
これらの問題をとくためにも、素数を単に覚えるだけでなく、判定する方法を覚えて素数を見つけられるようにしましょう。
素数を見つける方法
素数を見つける方法は、
- 2以外の2の倍数は素数ではない
- 3以外の3の倍数は素数ではない
- 5以外は5の倍数は素数ではない
- 7以外は7の倍数は素数ではない
・・・
と、素数の倍数を消していきます。残ったものが素数となります。この方法は、古代ギリシアの科学者エラトステネスが考案したもので「エラトステネスのふるい」と呼ばれています。
では、具体的に素数を見つけていきます。
1~20までの素数
1~20までの素数は、2,3,5,7,11,13,17,19の8個です。これらは最も重要な素数なので,ぱっと分かるように覚えておくとよいでしょう。
上の方法で、素数を見つけていくと、
- 2以外の2の倍数は素数ではない → 2の倍数の4, 6, 8, 10, 12, 14, 16, 18, 20が消される

- 3以外の3の倍数は素数ではない → 3の倍数の9、15も消される

5の倍数、7の倍数もすでに消えているので、残った数字が素数になります。11, 13, 17, 19は、九九に出てこない、あまりなじみのない数字ですね。九九に出てくる数字は、〇×△の形になっているので、一の段や、×1を除けば、素数ではありません。
21~50までの素数
21~50までの素数は、23, 29, 31, 37, 41, 43, 47の 7個です。
判定方法で、
- 2以外の2の倍数は素数ではない
- 5以外は5の倍数は素数ではない
ということから、2,5以外は,一の位は1,3,7,9のいずれかであることがわかります。この素数の性質は、判定を簡単にする重要なものですから、しっかり覚えておきましょう。一の位が、2, 4, 5, 6, 8, 0を消すと次のようになります。

次に,3と7の倍数を消していきます。
- 21, 27, 33, 39は,3の倍数なので素数ではない
- 49は,7の倍数なので素数ではない
残った数字が素数となります。

21,27,49は九九に表れる数ですし、33,39が3の倍数になるのは簡単に分かるので,50までの判定は簡単ですね。
51~100までの素数
51~100までの素数は、53, 59, 61, 67, 71, 73, 79, 83, 89, 97の 10個です。
51~100までも同じ判定方法で素数を見つけていきましょう。一の位は1,3,7,9のいずれかであることから、
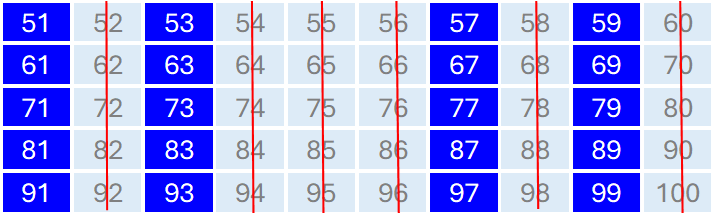
次に,3の倍数を消していきます。
- 51, 57, 63,69, 81,87, 93, 99は,3の倍数なので素数ではない
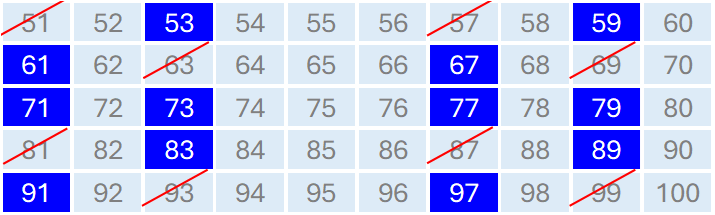
このうち,51(=3×17), 57(=3×19), 87(=3×29)は,3の倍数であることが分かりづらいので注意してください。3の倍数は,各位の和が3になることから判定できることを使って確認してください(51→5+1=6, 57→5+7=12, 87→8+7=15)。
最後に、7の倍数を消します。
- 77, 91は,7の倍数なので素数ではない。
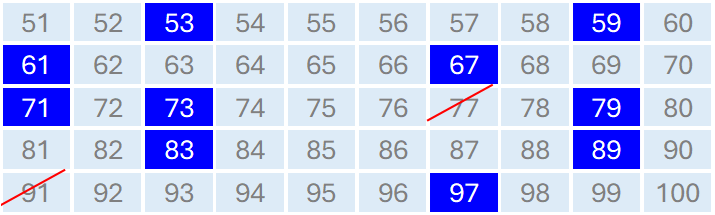
ここで特に注意する数字は,91(=7×13) です。7の倍数になることを見落とさないように、これはしっかり覚えてしまいましょう。
まとめ
1~100までの数について、素数の判定方法を説明しました。
- 2,5以外は,一の位は1,3,7,9のいずれかである
ということから、素数の候補をかなり絞り込むことができます。残った数字から3の倍数と7の倍数をのぞいていけば、100までの素数を見つけることができます。1~100の中の素数は,下の表のように,2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97の25個です。
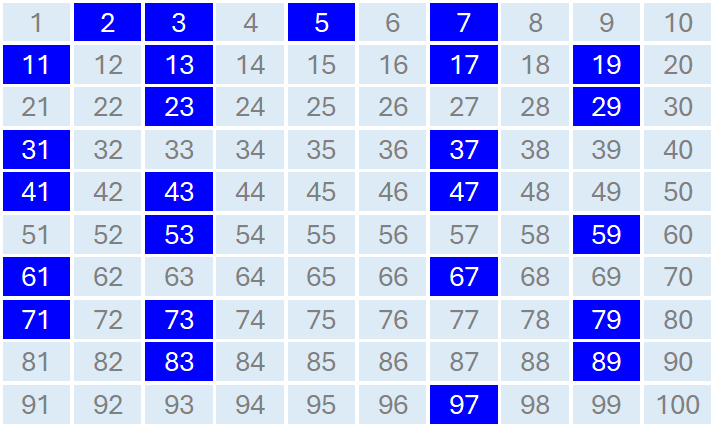

1~20までの素数は、よく使うのでしっかり覚えておきましょう。それより大きいものは丸暗記するよりも,上で説明した判定方法を覚えて素数か判断できるようにしましょう。

コメント