
今回は、ご石をならべる問題です。「方陣算」と言われています。計算の式を覚えるのではなくて、図をかいて理解して解いていくことがポイントです。問題に図がないものは、簡単な図をかいて考えていきましょう。
解説
中実方陣ーご石を中までぎっしりならべる
ご石の個数
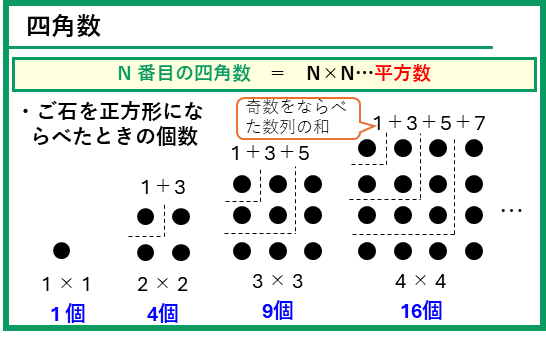
ご石を正方形の形に、中までぎっしりならべたものを「中実方陣」といいます。

1辺に6個ならべた場合は、正方形の面積と同じように、
6×6=36(個)
で求めることができます。このように、ご石を正方形の形にならべた「中実方陣」のご石の数は、同じ数を2回かけた数になります。この数を「四角数(または平方数)」といいます。次のように考えると、「等差数列」で勉強した、奇数をならべた数列の和とも考えられます。
外側ひとまわりの個数
外側ひとまわりのご石の個数は、どうなるでしょうか?
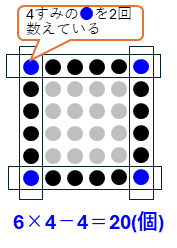
正方形のまわりの長さと同じよに、6×4で計算すると、4すみのご石を2回数えることになるので、その分をひいて、
6×4-4=20(個)
となります。上の図ように、外側の1列、1行を囲って、4すみが重なっていることを確認しましょう。また、下の図のように、
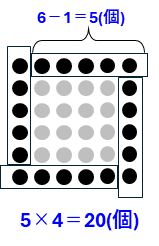
重ならないように、5個ずつのかたまりが4つとして求めることもできます。この分け方も重要なので、図として覚えておきましょう。
ご石を正三角形にならべる
ご石の個数
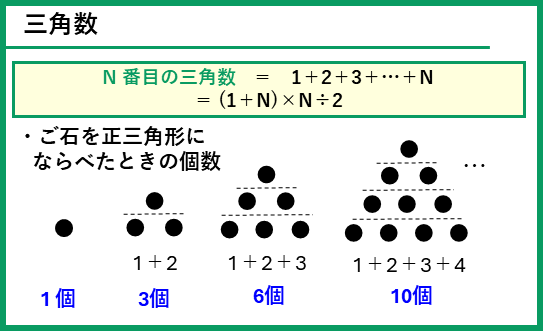
次に、ご石を正三角形にならべた場合を考えていきます。
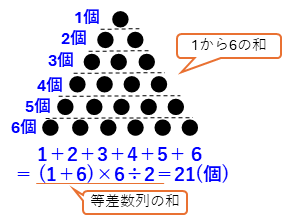
1辺のご石の数が6個の場合は、1だん目が1個、2だん目が2個、…、6だん目が6個ならんでいるので、1から6の和になります。等差数列の和として求めることができます。
1+2+3+4+5+6=(1+6)×6÷2=21(個)
ご石を正三角形の形にならべたときの、ご石の数を「三角数」といいます。
外側ひとまわりの個数
外側ひとまわりのご石の個数は、正方形にならべた場合と同じように考えられます。
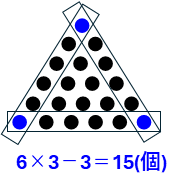
1辺が6個で、6×3で計算すると、頂点にある3個のご石を2回ずつ数えることになるので、
6×3-3=15(個)
となります。また、かさなりがないように、分けて、

5×3=15(個)
で求めることもできます。
中空方陣ー中があいている
ご石を、真ん中があいている形で正方形にならべたものを「中空方陣」といいます。
ご石の個数
中空方陣では、4つの同じ長方形に分けて考えます。3列の中空方陣の例を考えます。
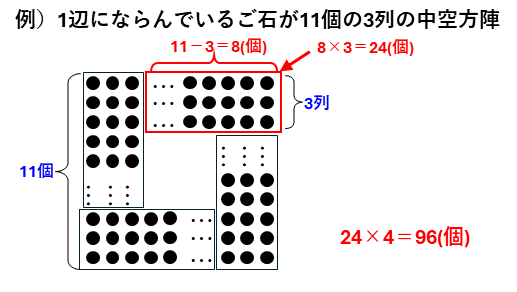
1辺に並んでいる個数
ご石の数から、1辺に並んでいる個数を求める問題もあります。これも、4つの同じ長方形に分けて考えます。
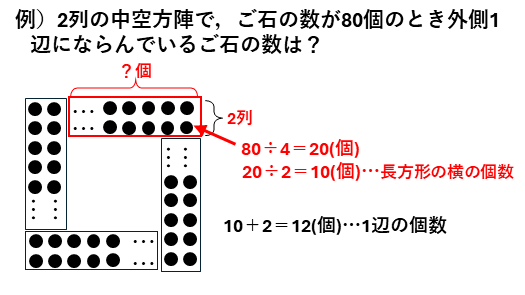
練習問題
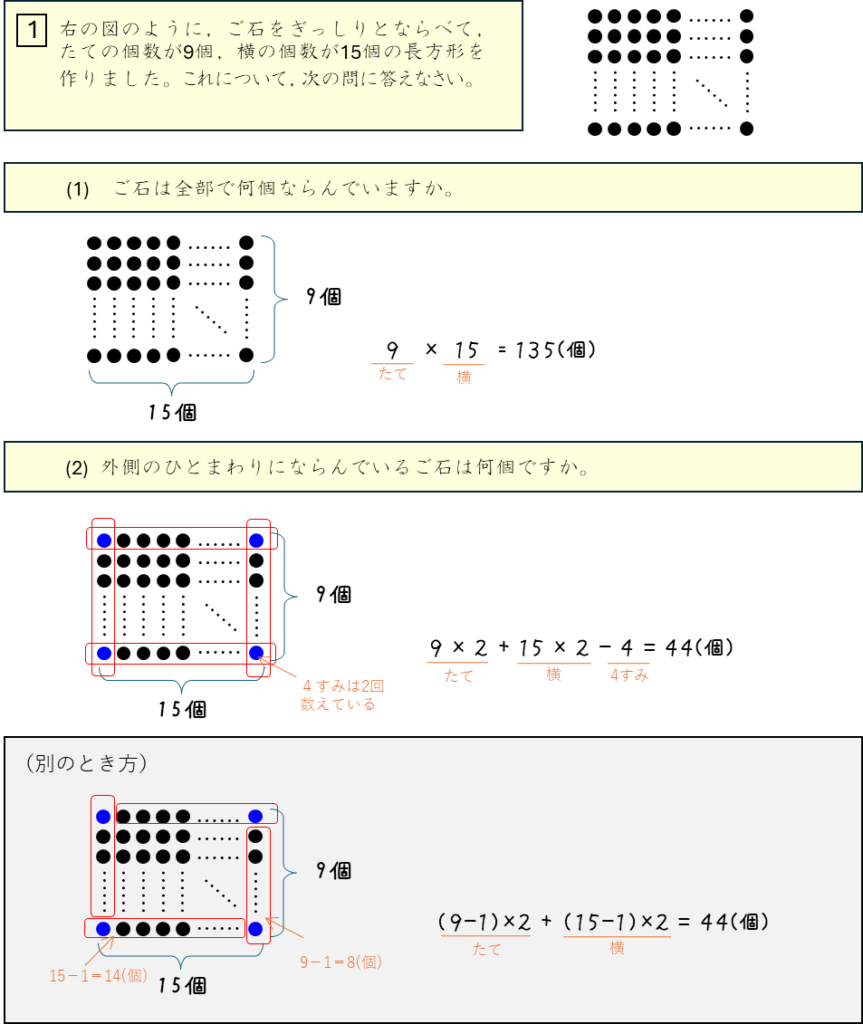
ご石を長方形にならべる

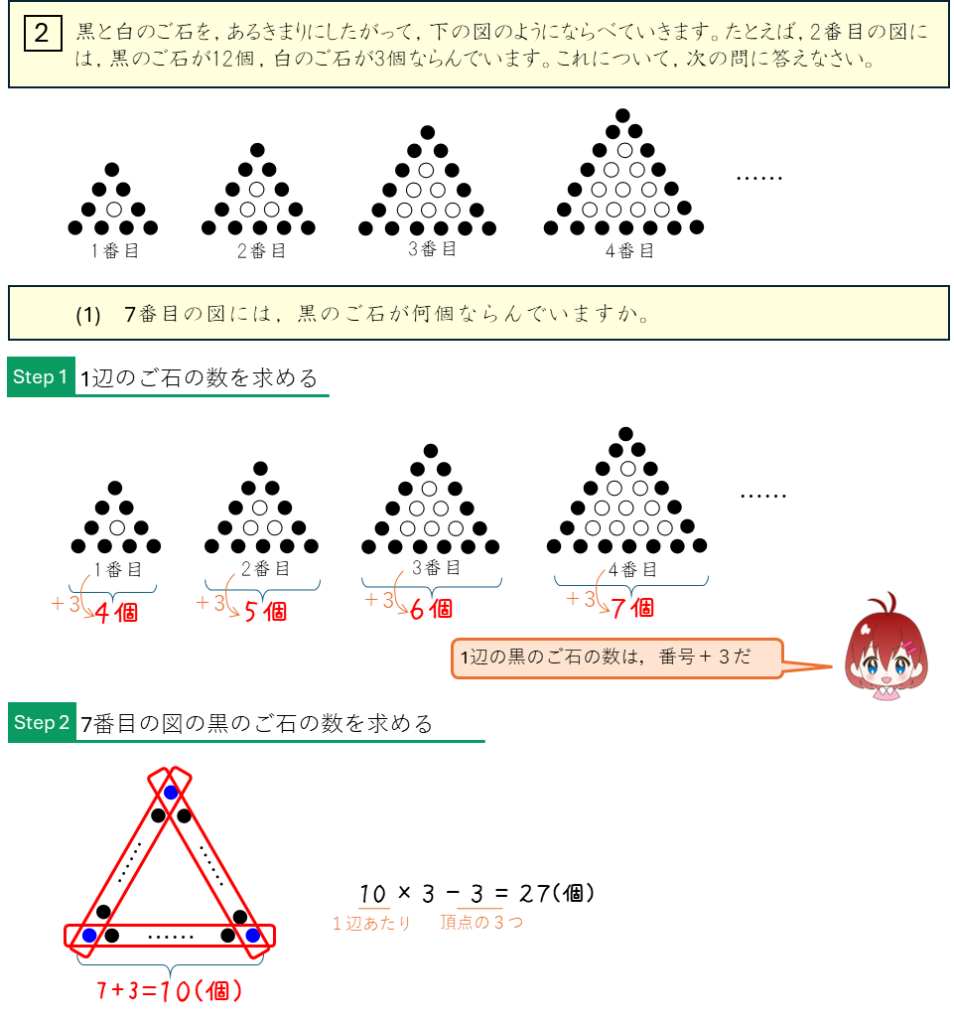
ご石を正三角形にならべる
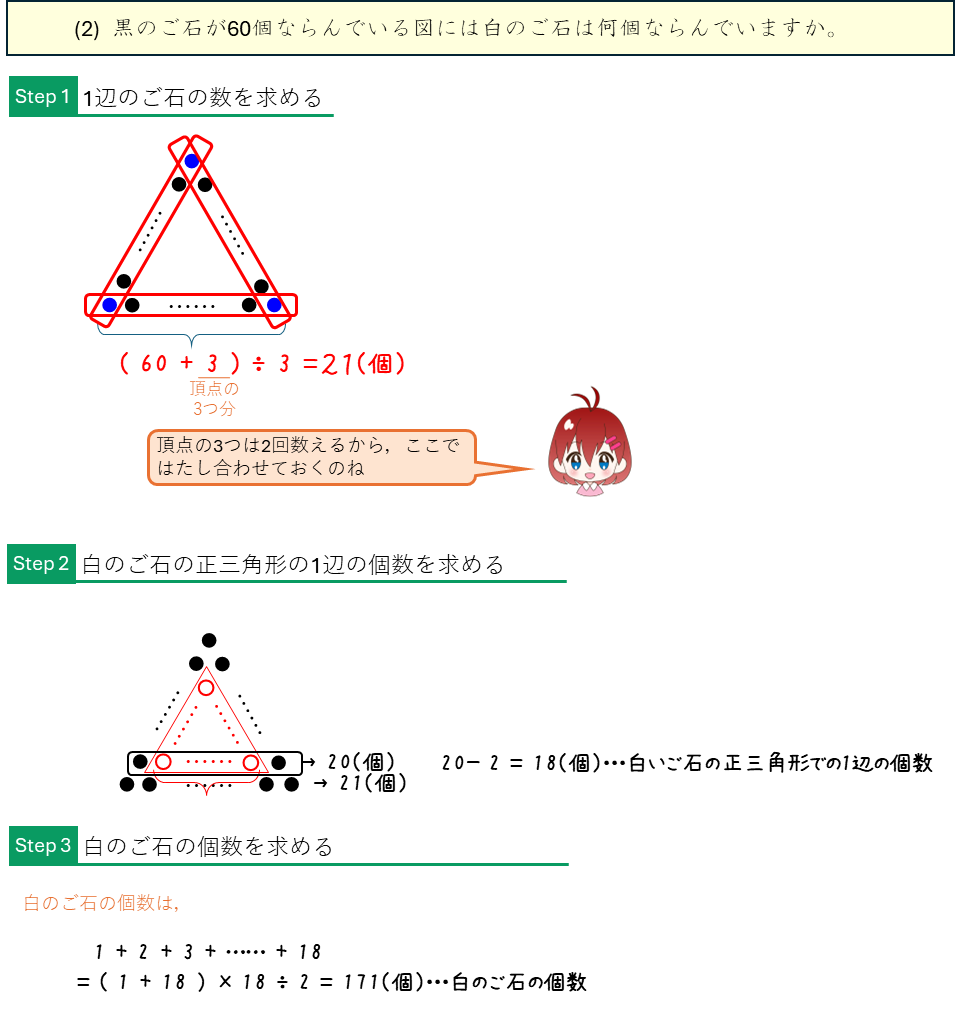
ご石を正方形にならべる(中実方陣)ー1列ふやす
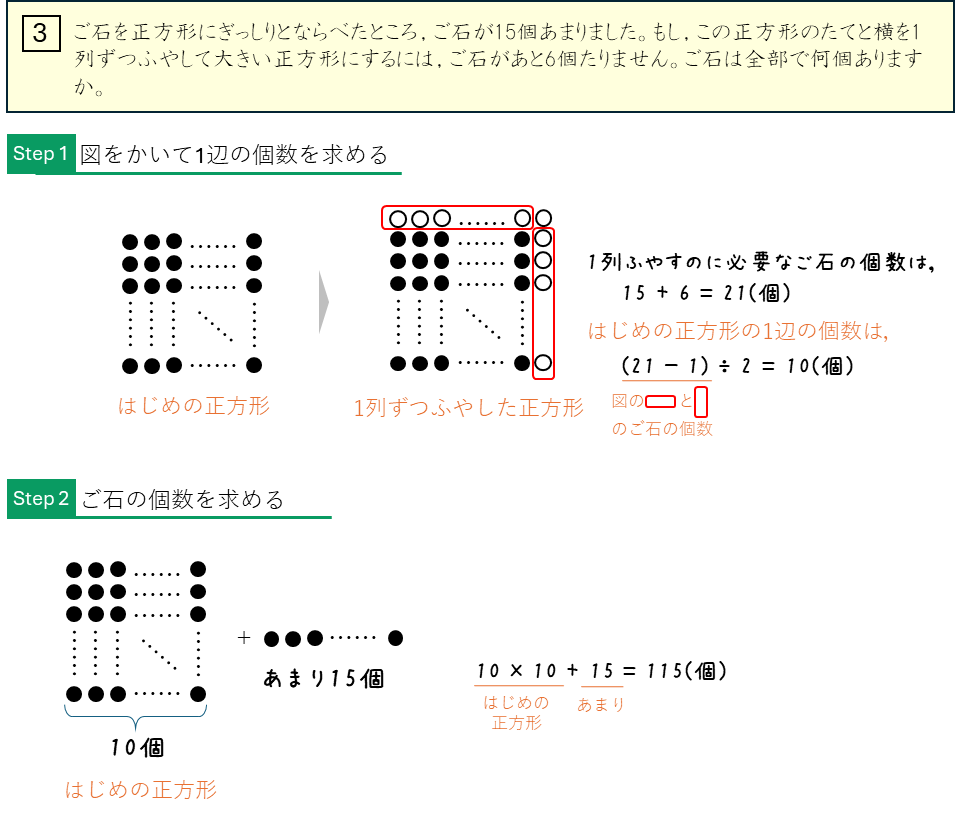
ご石を正方形にならべる(中空方陣と中実方陣)
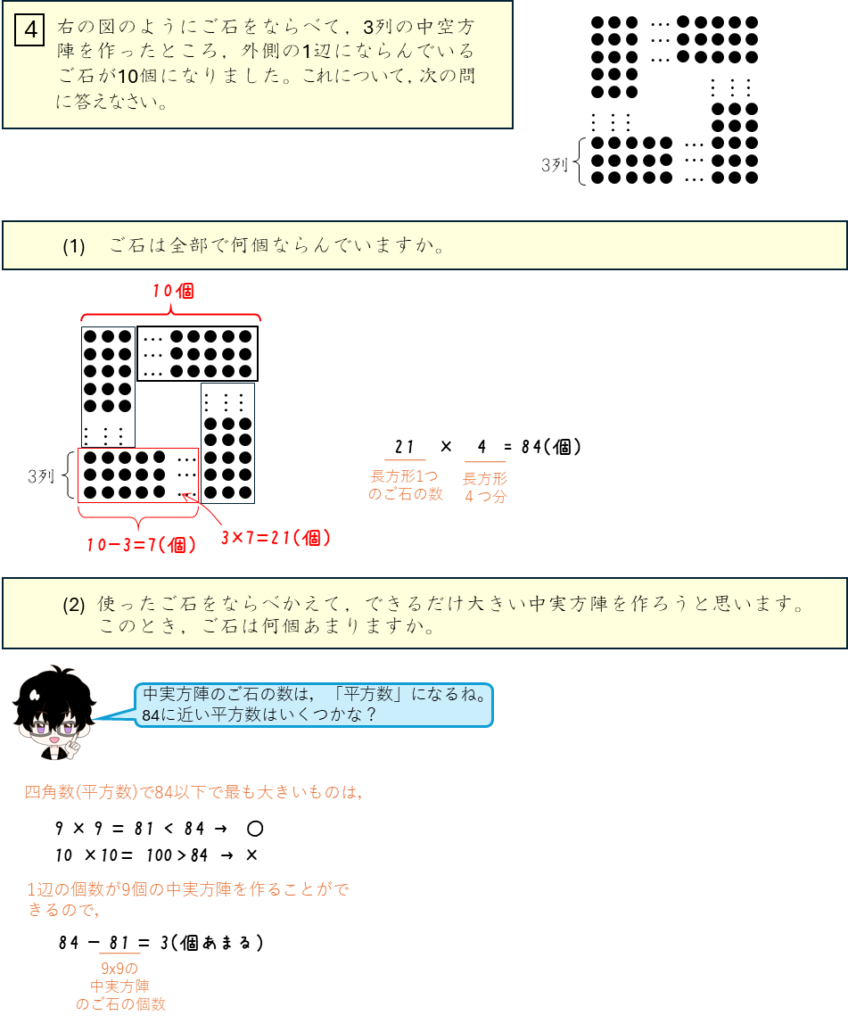
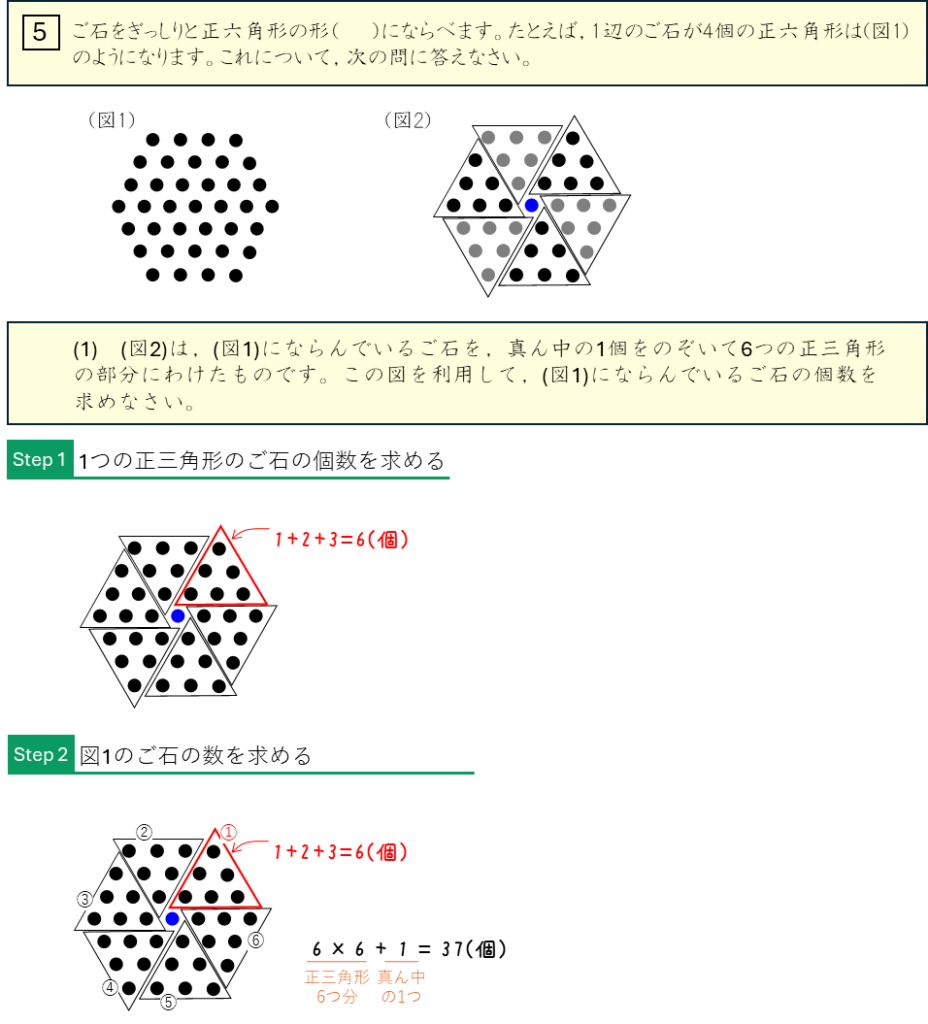
ご石を正六角形にならべる

今回のご石をならべる問題(方陣算)は、理解できたかな?

[5]の正六角形にならべる問題が難しかったわ。6つの正三角形に分けるなんて気づかなかった

そうだね。これでキレイに分けることができるのは、面白いね。他の問題も同じように、ご石を規則性をもって分割して考えることがポイントだ。図にかいて考えれば解けるので、分割の方法をしっかり身につけてね

コメント