
今回は、和と差に関する特殊算の1つの「差集め算」について勉強します。あまりと不足の差が、1人や1個ずつの差をみんな集めた全体の差になっているを理解するのが、1つのポイントとなっています。あまりと不足の差に着目するので「過不足算」とも呼ばれます。線分図や、差に着目した図(ここでは「おだんご図」と呼んでいます)をかいて、しっかりイメージを作っていきましょう。
解説
差集め算の基本問題と解法
差集め算(過不足算)-あまりと不足
次の例題を考えてみましょう。

まずは、線分図をかいて「あまりと不足の差」が「全体の差」になることを確認します。
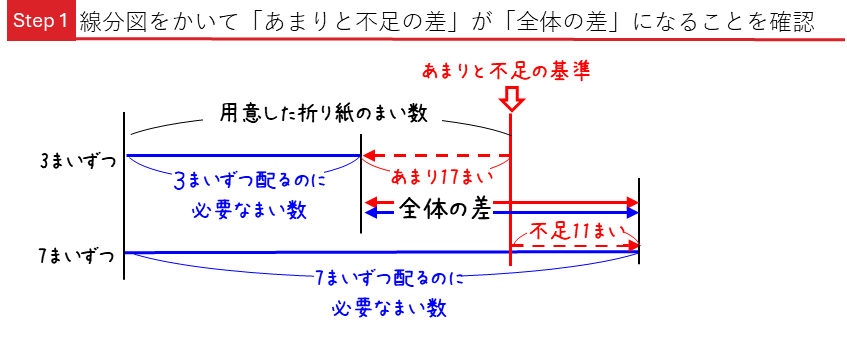

3まいずつ配った場合はあまりが17まい、7まいずつ配った場合は11枚不足となります。線分図から、「あまりと不足の差」 (図の赤色の差) 17+11=28(まい)
が,「全体の差」つまり,「全員に3枚ずつ配るのに必要なまい数と,全員に7枚ずつ配るのに必要なまい数の差」(図の青の差)と等しくなっていることが分かります。
では、次に、3まいずつ配った場合と、7まいずつ配った場合を比べるために、「つるかめ算」と同じように「おだんご図」をかいてみましょう。
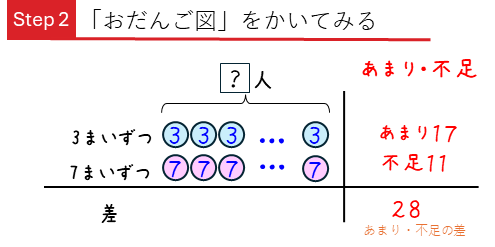
左がわに1人あたり3まいずつ、7まいずつを配ったことを図にかいて、右側にそれぞれの場合のあまりと不足をかきます。下の行には、差をかきます。Step 1からあまり・不足が28になります。
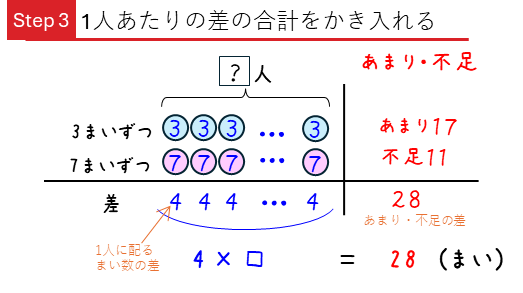
左がわにも差を書き込みます。「1人あたりのまい数の差が4まいで、それを全員分集めたもの」が「全体の差」(線分図の青の差)になり、あまりと不足の差(線分図の赤の差)と等しくなります。

したがって、子どもの人数は、
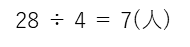
となります。
差集め算(過不足算)-あまりとあまり
2番目の例題です。

この問題では、2つの場合でともに、あまりが出ます。(1)と同じようにまずは線分図をかいてみましょう。
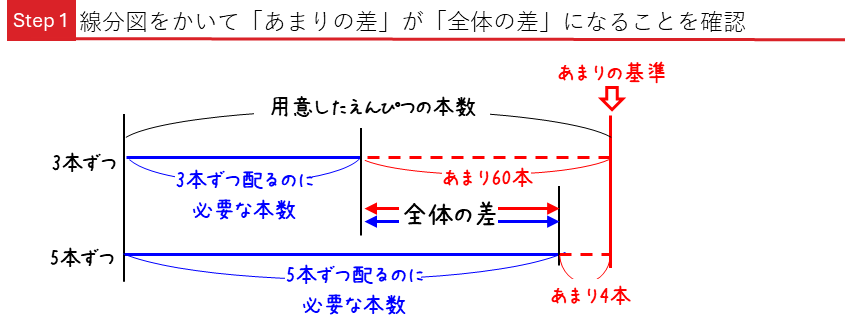

この場合は、2つのあまりの差が全体の差(図の赤色の差)になることが分かります。
3本ずつ配った場合のあまりが60本、5本ずつ配った場合は4本となります。線分図から、「あまりとあまりの差」 (図の赤色の差)は、 60-4=56(本)になります。
これは、「全体の差」つまり,「全員に3本ずつ配るのに必要な本数と,全員に5本ずつ配るのに必要な本数の差」(図の青の差)と等しくなっていることが分かります。
では、(1)と同じよように「おだんご図」をかいてみましょう。
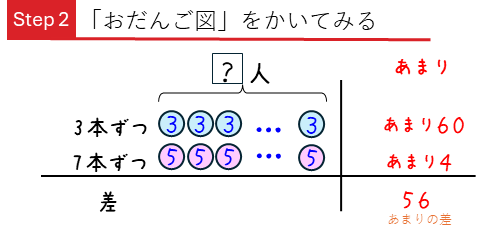
さらに、1人あたりの差とその合計もかき入れます。
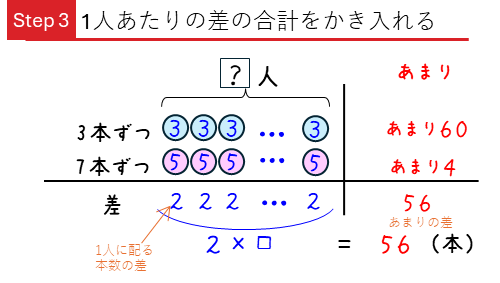
左がわにも差を書き込みます。「1人あたりの本数の差が2本で、それを全員分集めたもの」が「全体の差」(線分図の青の差)になり、あまりの差(線分図の赤の差)と等しくなります。
子どもの人数は、
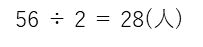
となります。
差集め算(過不足算)-不足と不足
3番目の問題では、2つの場合で不足が出ます。

線分図をかいて、「不足の差」が「全体の差」と等しいことを確認しましょう。
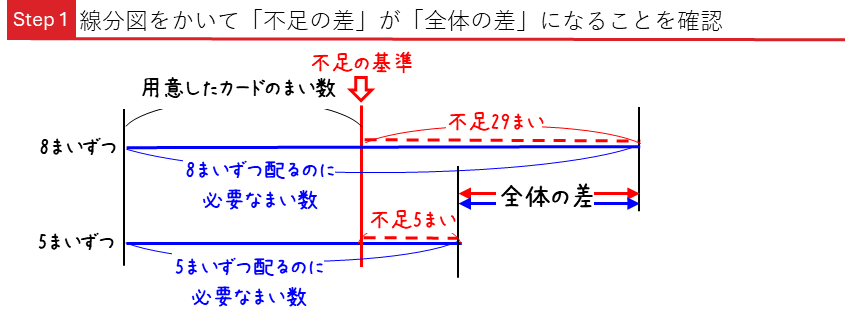

8まいずつ配った場合に29枚足りなくなり、5まいずつ配った場合に5枚足りなくなります。線分図から、「不足と不足の差」 (図の赤色の差)は、 29-5=24(まい)になります。
これが、「全体の差」つまり,「全員に8まいずつ配るのに必要なまい数と,全員に5まいずつ配るのに必要なまい数の差」(図の青の差)と等しくなっていることが分かります。
では、次に、(1)、(2)と同じよように「おだんご図」をかいて解き進めましょう。
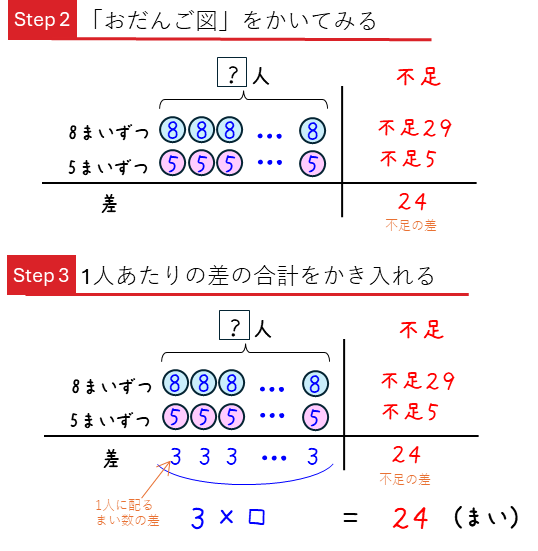
全体の差は、不足と不足の差から24まいであることがわかっていて、1人あたりの差が3まいですから、子どもの人数は、
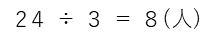
となります。
「あまりと不足」、「あまりとあまり」、「不足と不足」の3つの例題を解きました。ポイントは、
1)「あまりと不足の差」、「あまりとあまりの差」、「不足と不足の差」が「全体の差」と等しくなる
また、
2)「全体の差」は、「1人あたりの差をすべて集めたもの」である
から、求める人数は、

で計算できます。、はじめは、1)は線分図を、2)は「おだんご図」をかいて、イメージできるようにしましょう。

「あまりと不足の差」、「あまりとあまりの差」、「不足と不足の差」が「全体の差」と等しくなることがイメージできるようになったら,線分図をかくことをスキップして、2)の「おだんご図」から解きはじめていいよ
差集め算の応用問題ー数をそろえる
基本問題では、全員に同じ数だけ配りました。応用問題では、配る数が異なる場合がありますが、これは、同じ数だけ配った場合に直して考えていきます。

基本問題と同じように、「おだんご図」をかきます。
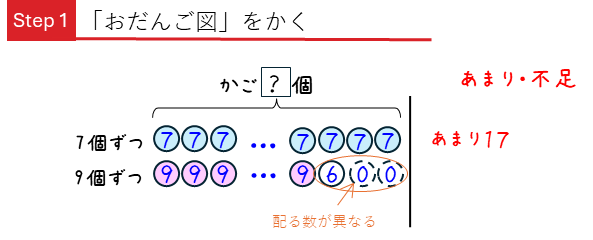
この問題では、9個ずつ配った場合に、最後の3つのかごは、6個入っているかごと、何も入っていないかご2つになります。これをすべてのかごに9個入れたと考えると、

このように、21個不足となります。この形にできれば、基本問題と同じように解けます。
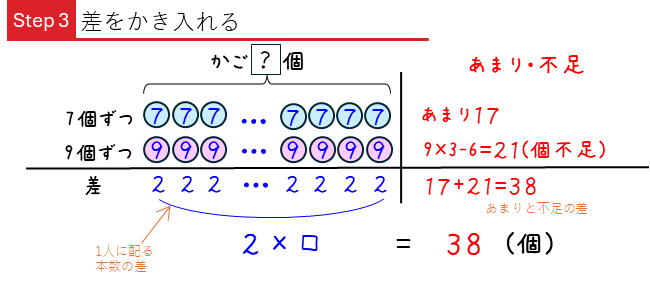
これから、かごの数とクリの個数は、次のように計算できます。

この問題の解き方のように、差集め算の3つ目のポイントは、
3)配る数をすべて同じにする
ことです。したがって、次のような解くこともできます。


ここまでは大丈夫かな?じゃあ、練習問題に取り組んでいこう
練習問題
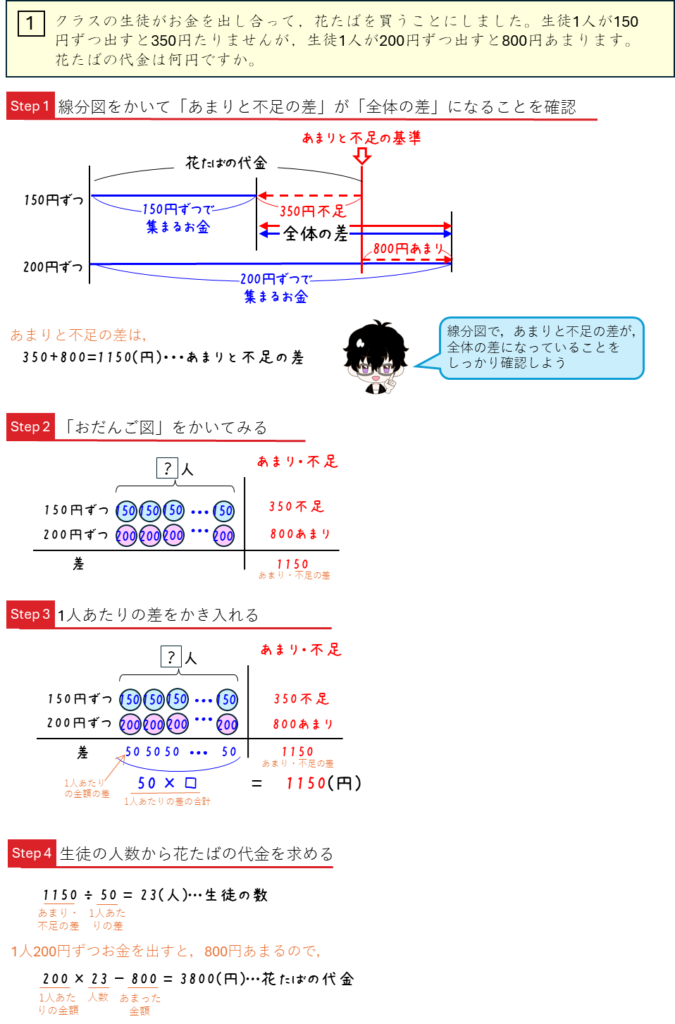
差集め算ーあまりと不足
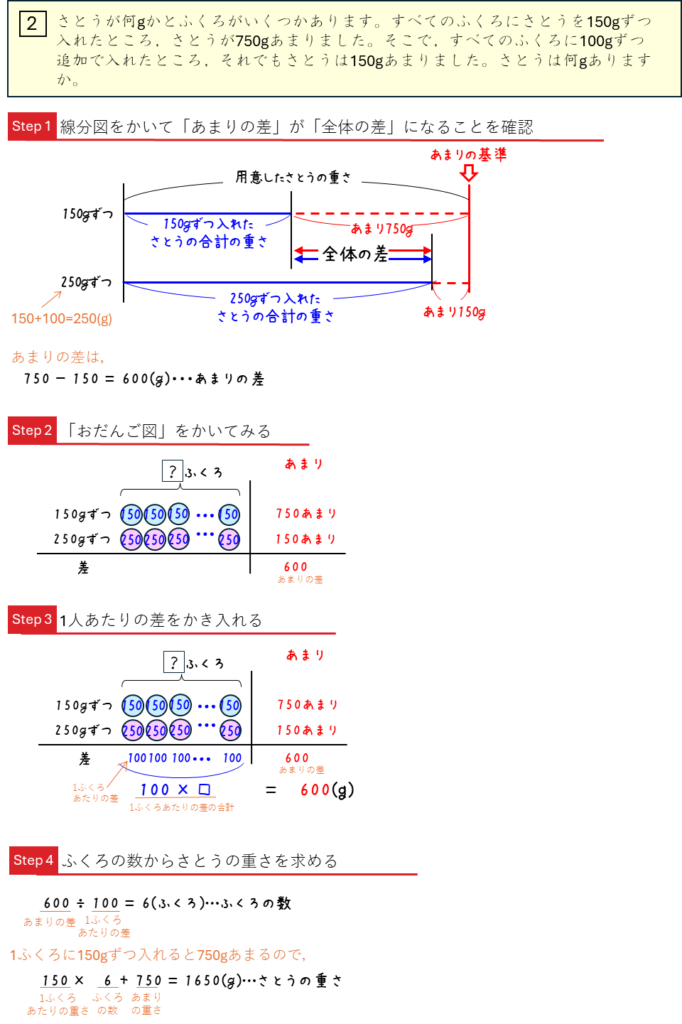
差集め算ーあまりとあまり
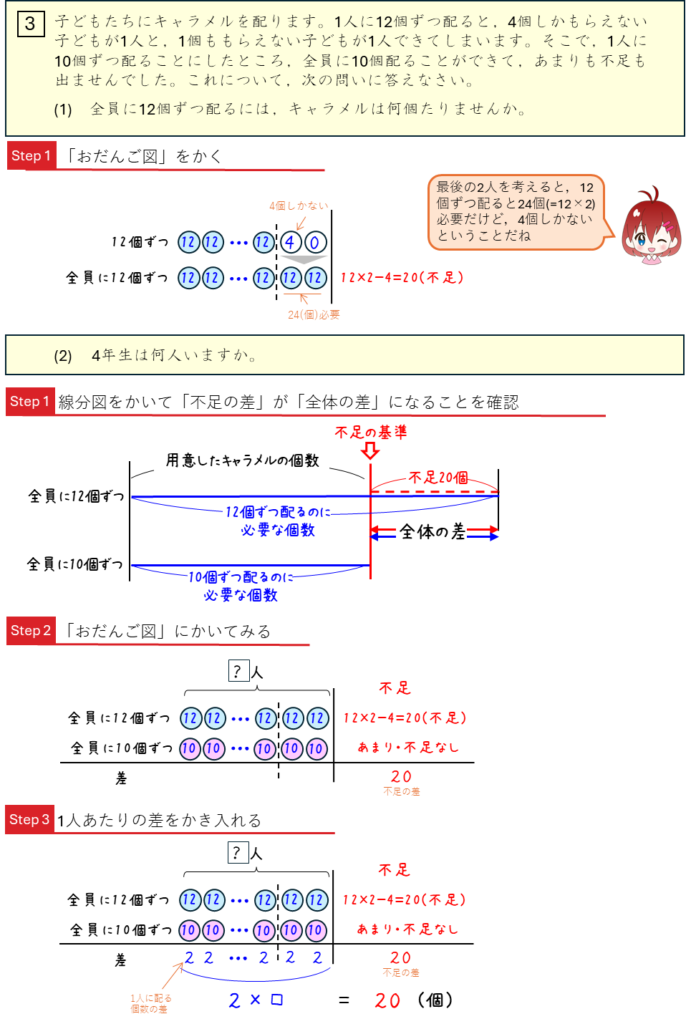
差集め算ー数をそろえる

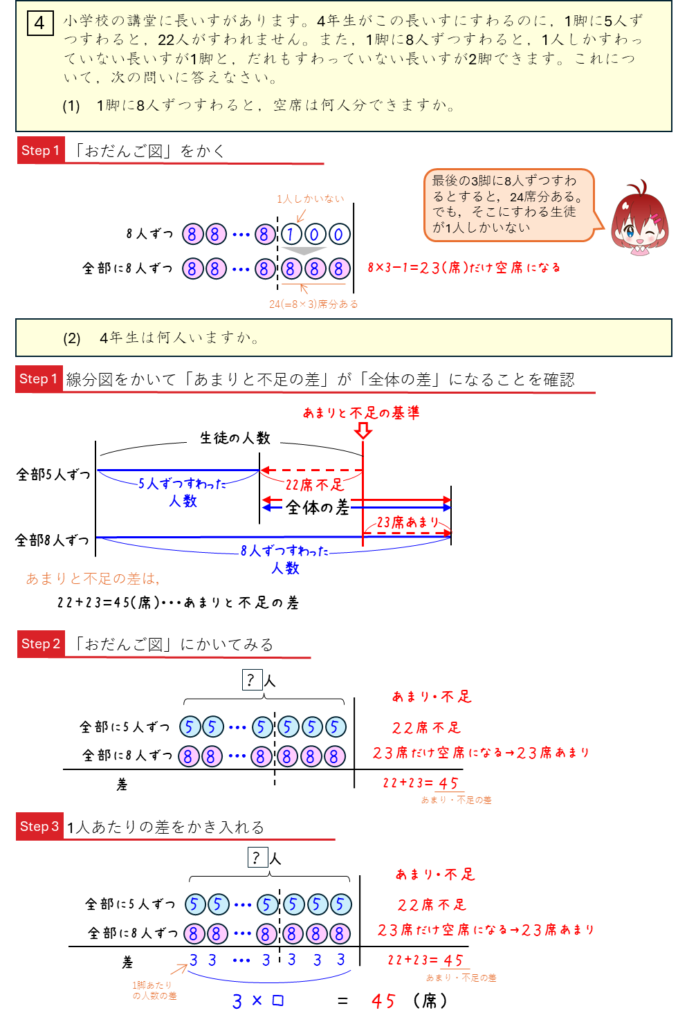

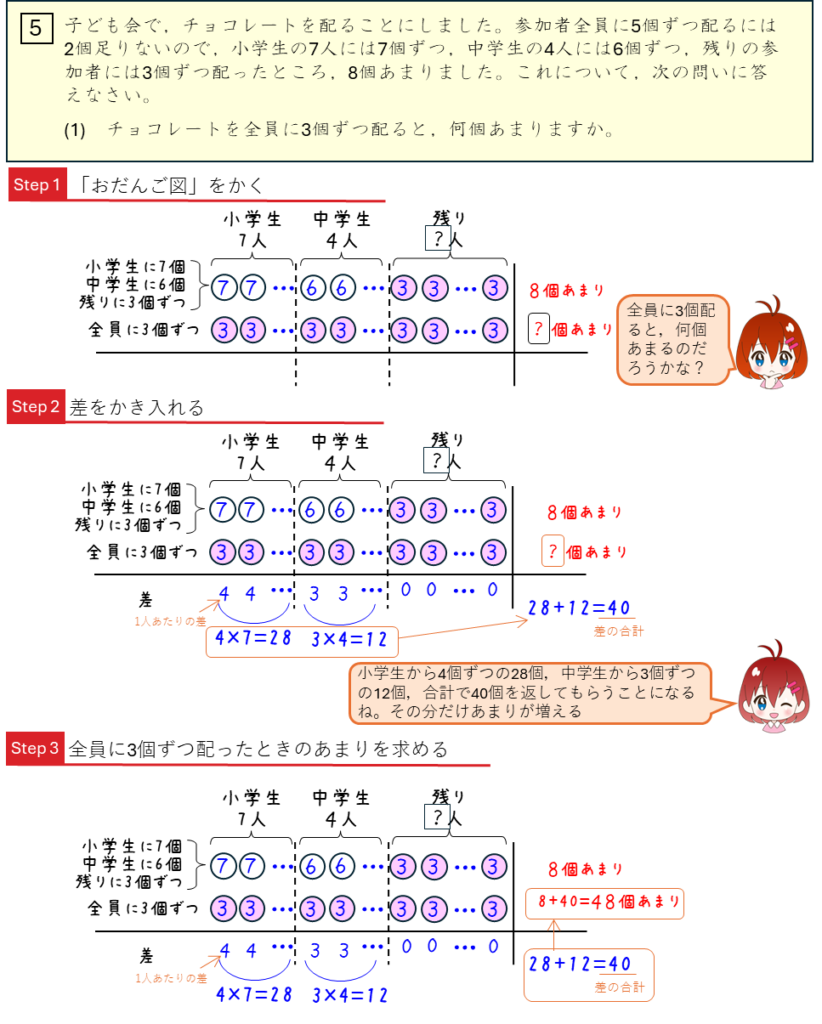
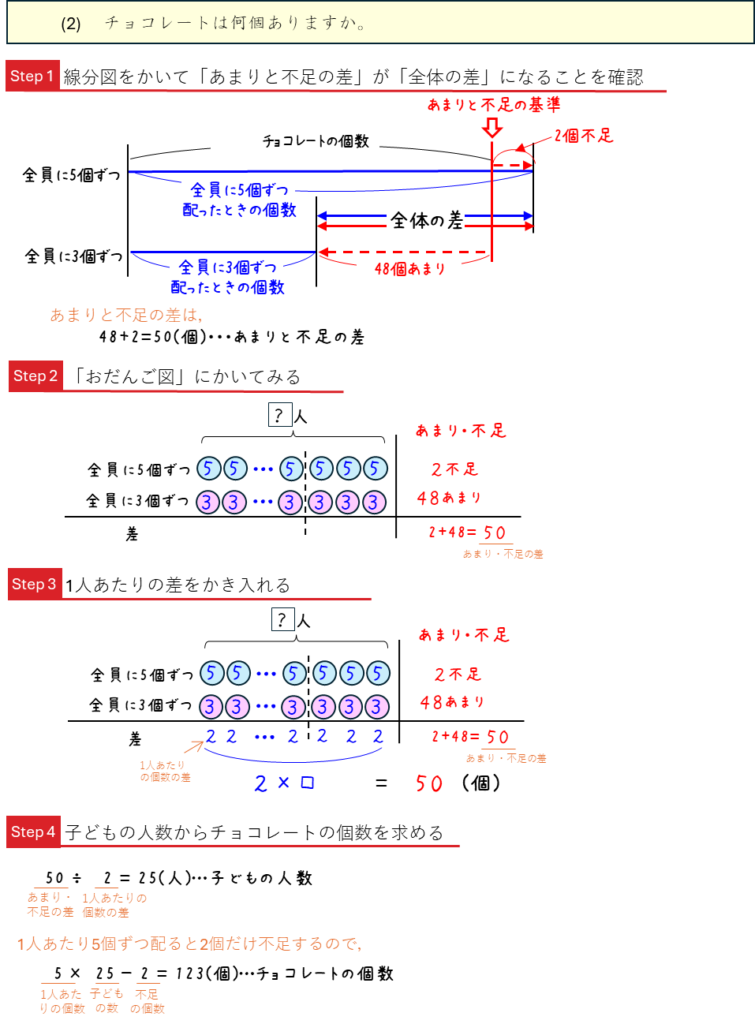

差集め算は、難しかったかな?

「不足・あまりの差」が「全体の差」になるところが、まだちょっとフワッとしているかな。あとは、図をかけば解くことができそう

いろいろな問題を繰り返して解いて、しっかりと理解していこうね

コメント