
今回は、分数のたし算とひき算を勉強します。これまでに勉強してきた公約数と公倍数の考え方がでてくるよ。
解説
分数には、
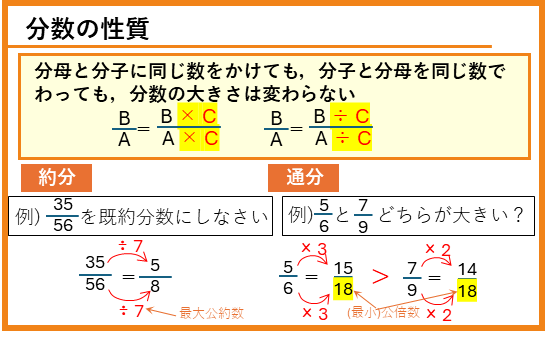
分母と分子に同じ数をかけても,分子と分母を同じ数でわっても,分数の大きさは変わらない
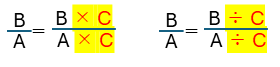
という性質があります。
約分
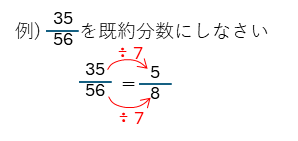
約分とは、「分数の分母と分子を公約数でわること」です。また、既約分数とは、「これ以上、約分できない分数」のことを言います。分母と分子を最大公約数でわることで、既約分数にすることができます。また、テストの解答では、分数を既約分数にして答えなければなりません。
通分
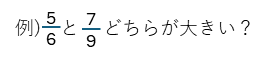
$\frac{5}{6}$と$\frac{7}{9}$は、直接は比較できません。このような場合、分数の性質を使って分母を同じ数にそろえることで比較することができます。
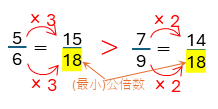
分母がことなる分数の「分母の公倍数を見つけてそれを分母とする分数にすること」を、通分と言います。分母を最小公倍数にそろえると、それぞれの数が小さくなるので計算が簡単になる場合が多いです。
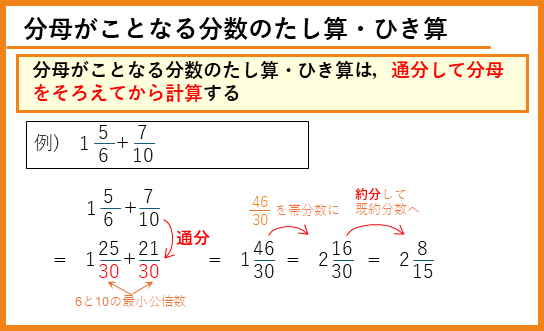
分母がことなる分数のたし算・ひき算
分母がことなる分数のたし算とひき算は、通分することで計算できます。

まとめ
練習問題
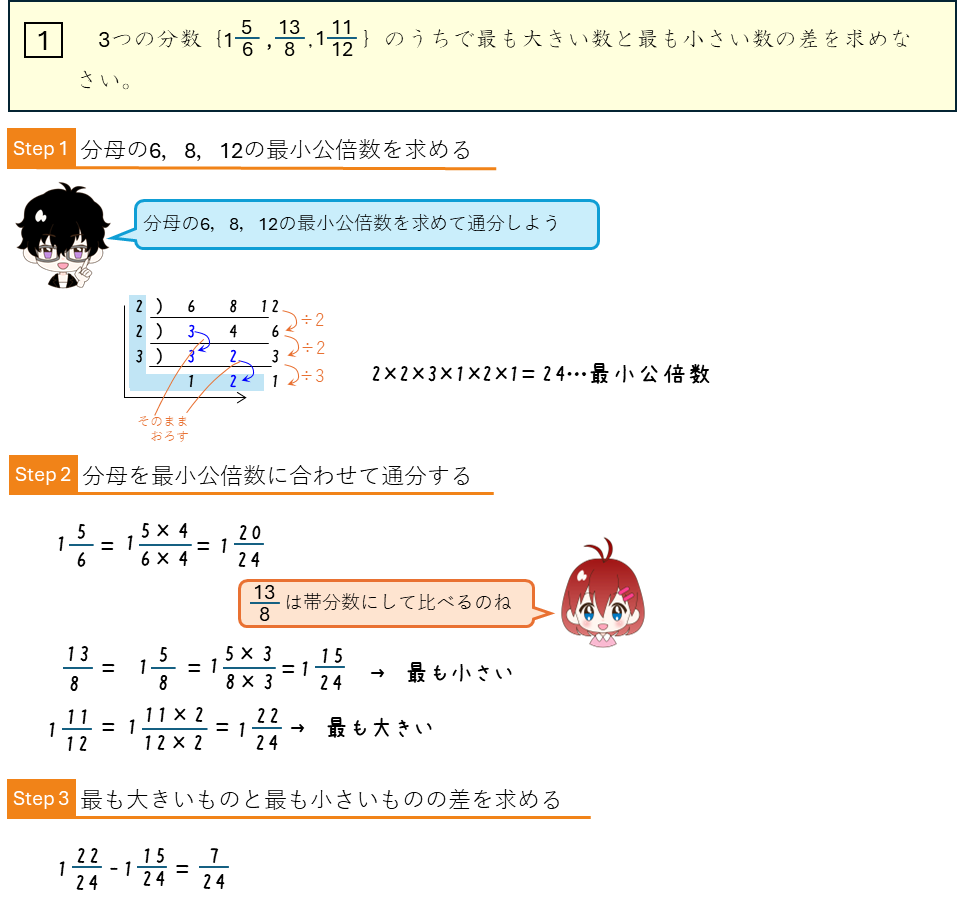
通分と分数のひき算
分数の性質の応用
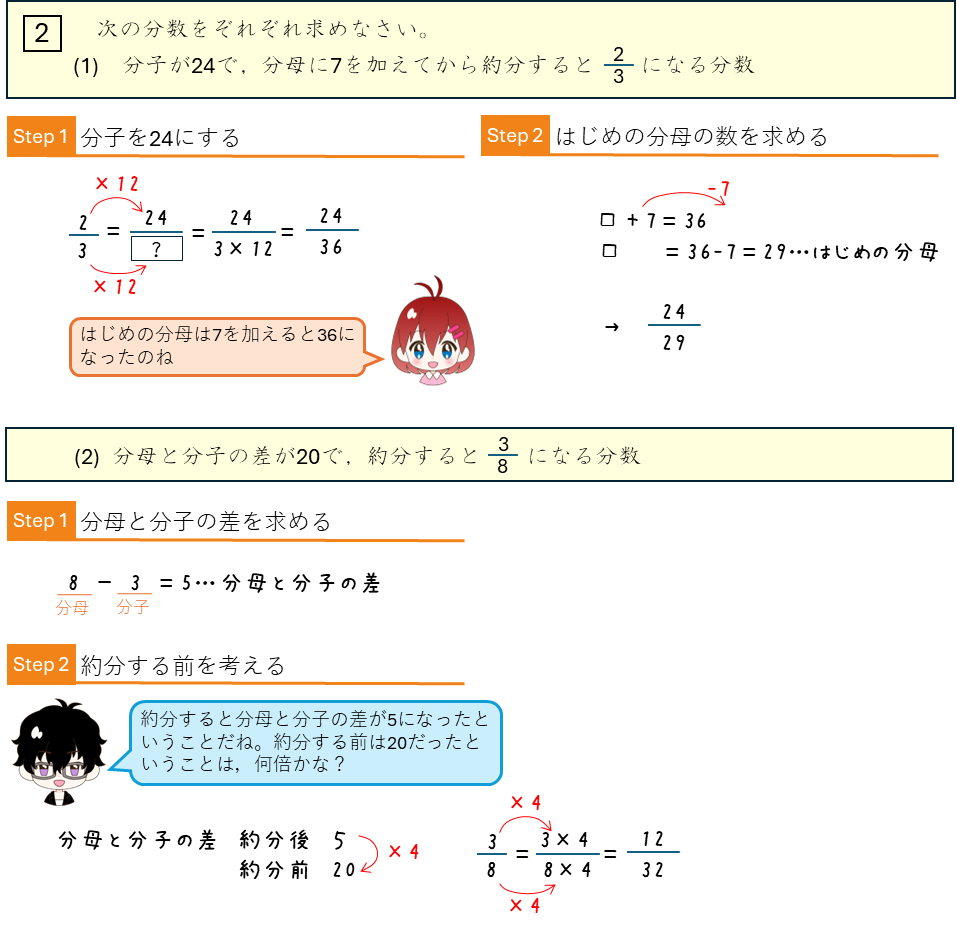
2つの分数の間の既約分数を求める
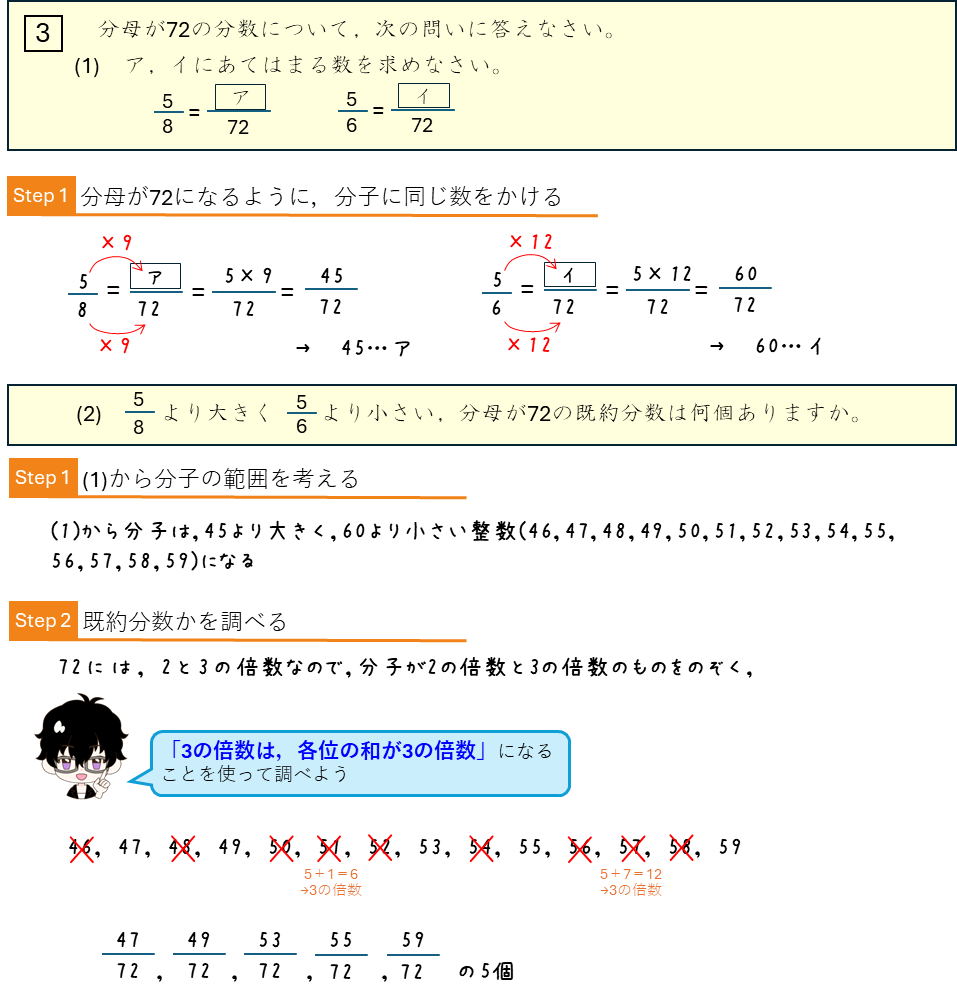
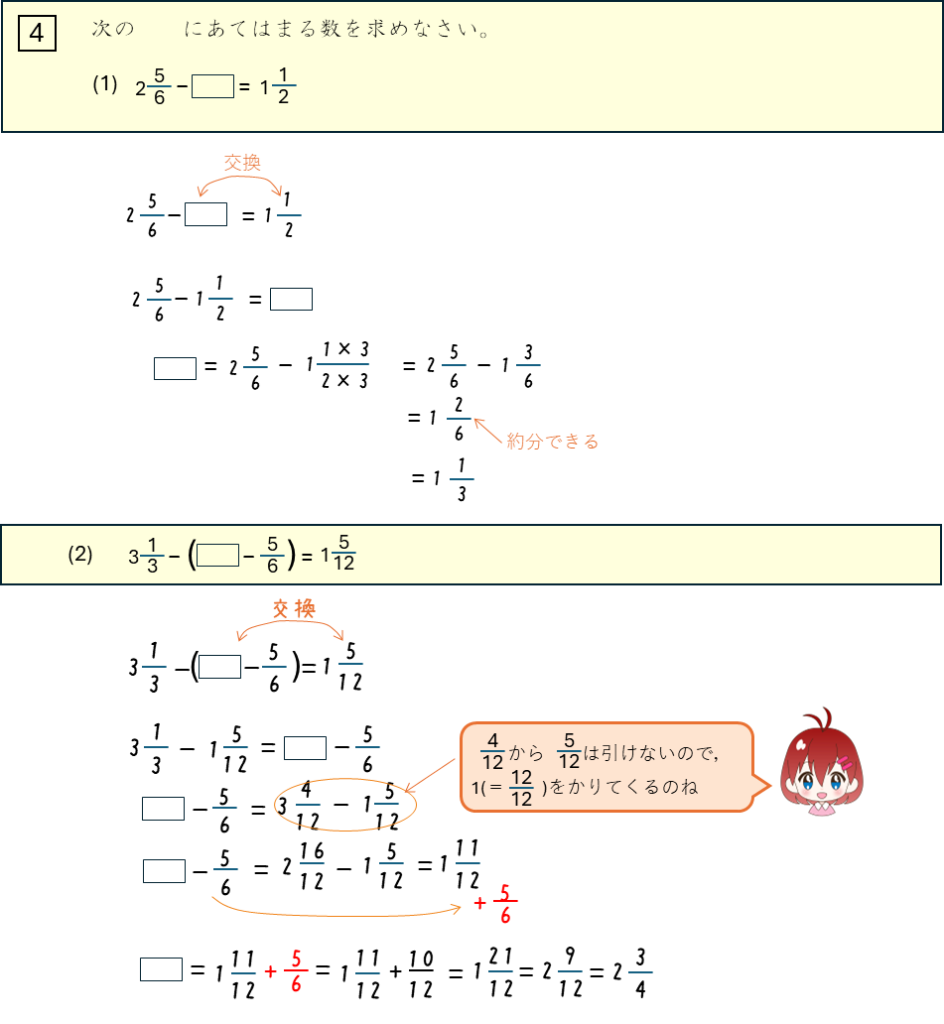
分数をふくむ逆算

分数をふくんだ少し複雑な逆算の問題だね。逆算のやり方は次のページを参考にしてください
中学受験 算数 解説:逆算②― 一瞬で解き進められる裏技を教えます!

今日の内容はどうだった?

[3]が難しかったかな

[3]の2つの分数の間にある既約分数を求める問題のように、単純な分数のたし算やひき算ではなくて、分数の性質を応用した問題もあるので、解き方を理解しておこう

コメント