
今回は、前回の「速さと比」を「旅人算」に応用します。旅人算は、5年上第16回で勉強したので、内容を確認しながら進めましょう。
旅人算では、線分図をかいて考えていきます。線分図の基本的なかき方は5年上と同じですが、2人が進んだきょりを比で表して解いていくところが新しいです。速さの比、道のり(きょり)の比、時間の比の関係を使うので、前回の内容を復習しながら解いていきましょう。
また、「速さのグラフと比」では、速さのグラフから「三角形」を見つけるのがポイントになります。新しい内容なので、しっかり理解しておきましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
旅人算のグラフの三角形
速さのグラフの問題を解くときに、図から三角形を見つけるのがポイントになります。4種類あるので、まとめて覚えておきましょう。
旅人算のグラフの三角形①ー2人がすれちがう
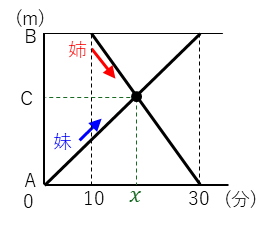
下のグラフのように、妹がA地点からB地点へ、姉がB地点からA地点へ向かっていて、C地点ですれちがうときの時間(x)を求めると言う問題です。ここで、姉と妹の速さの比は3:2です。

この問題では、下の三角形に注目します。
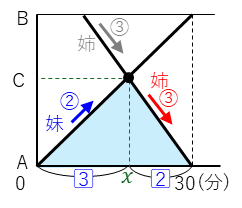
AC間を進むのにかかる姉と妹の時間の比は速さの逆比となります。

全体が30分で、これが5⃣となるので、xは、
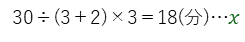
となります。
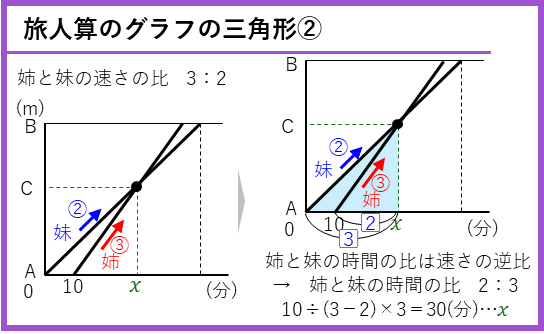
旅人算のグラフの三角形②ー一方が追いこす
次は、妹がA地点からB地点へ出発した後、遅れて姉がA地点からB地点に向かう場合です。下のグラフのように、C地点で姉が妹を追いこす時間(x)を求めると言う問題です。ここでも、姉と妹の速さの比は3:2です。

この問題ではA地点からC地点までの三角形に注目します。
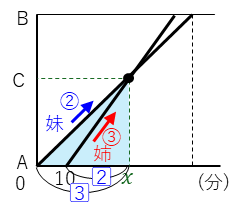
最初の問題と同じように、AC間を進むのにかかる姉と妹の時間の比は速さの逆比となり、

ここで、妹がAC間を進むのにかかった時間3⃣が求めるx、姉がかかった時間が2⃣となり、xは、
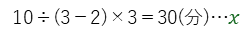
となります。
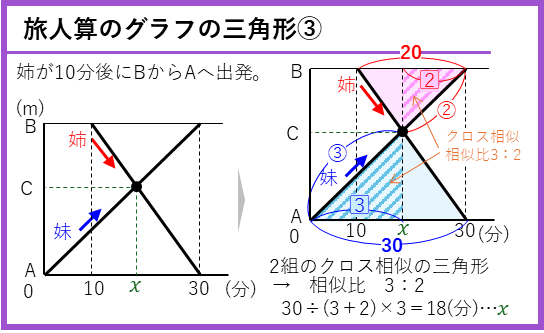
旅人算のグラフの三角形③ー2人がすれちがう(相似で解く)
次の例題では、相似を使った図形の問題として解きます。速さのグラフでは相似を使った解き方をよく使うので、覚えておきましょう。
妹がA地点からB地点へ出発し、姉がその10分後にB地点からA地点へ向かいます。C地点ですれちがうときの時間(x)を求めると言う問題です。
姉はBからAまで30-10=20分かかり、妹は30分かかります。
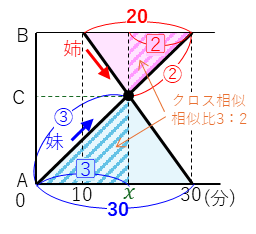
図形の中から、相似比が3:2の2組のクロス型相似の三角形を見つけることができます。これからxを求めると、
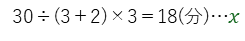
となります。
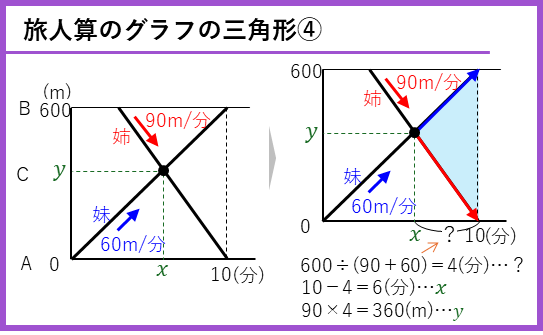
旅人算のグラフの三角形④ー2人がすれちがって同時に到着する
最後の三角形の問題は、比は使っていない5年上の内容です。姉と妹がC地点ですれちがって、姉はA地点、妹はB地点に同時に到着します。
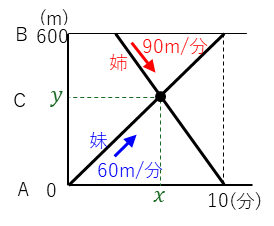
ここで注目するのは、右側の三角形です。
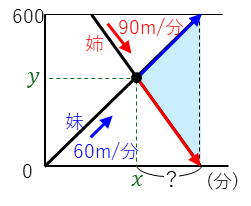
この部分は、姉と妹の2人でA地点からB地点の600m分を進むことになります。かかる時間は、
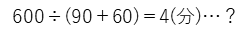
となるので、
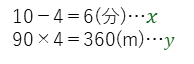
と解けます。
まとめカード
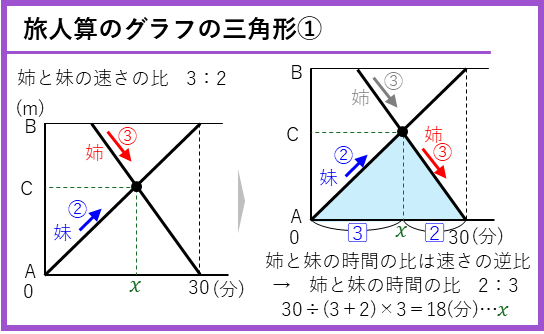

旅人算のグラフの4種類の三角形を解説しました。旅人算のグラフでは、三角形を見つけて解くということをぜひ覚えておきましょう。
練習問題
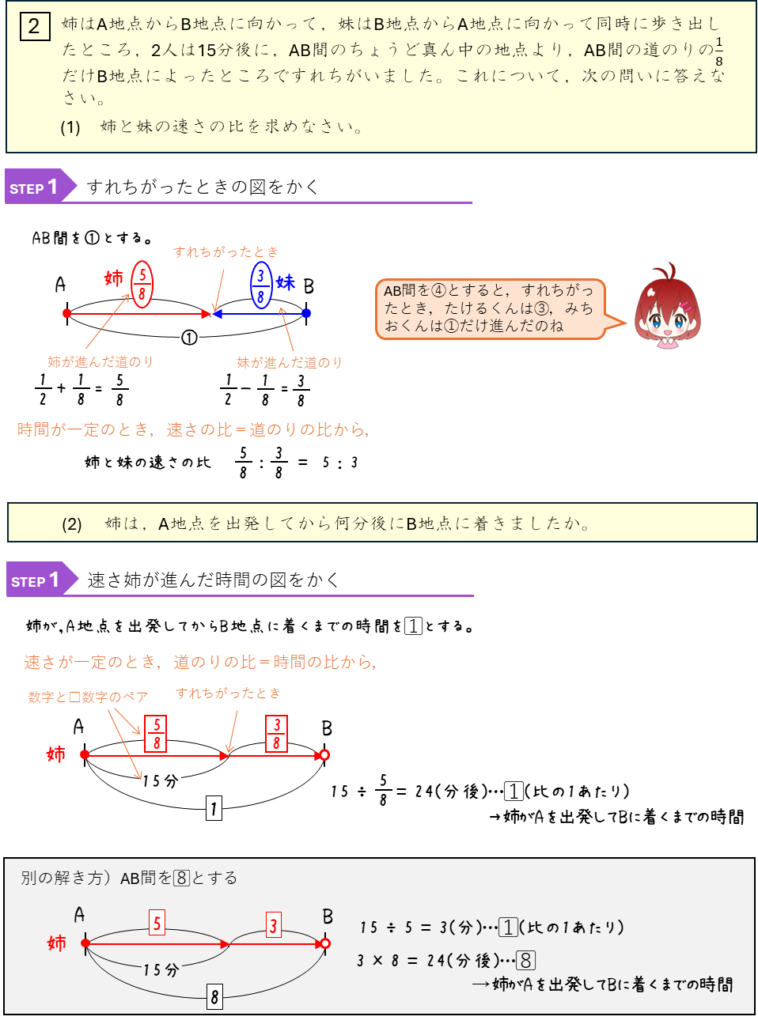
旅人算と比ー2人がすれちがう(一方が到着したときの残りの道のりが分かる)
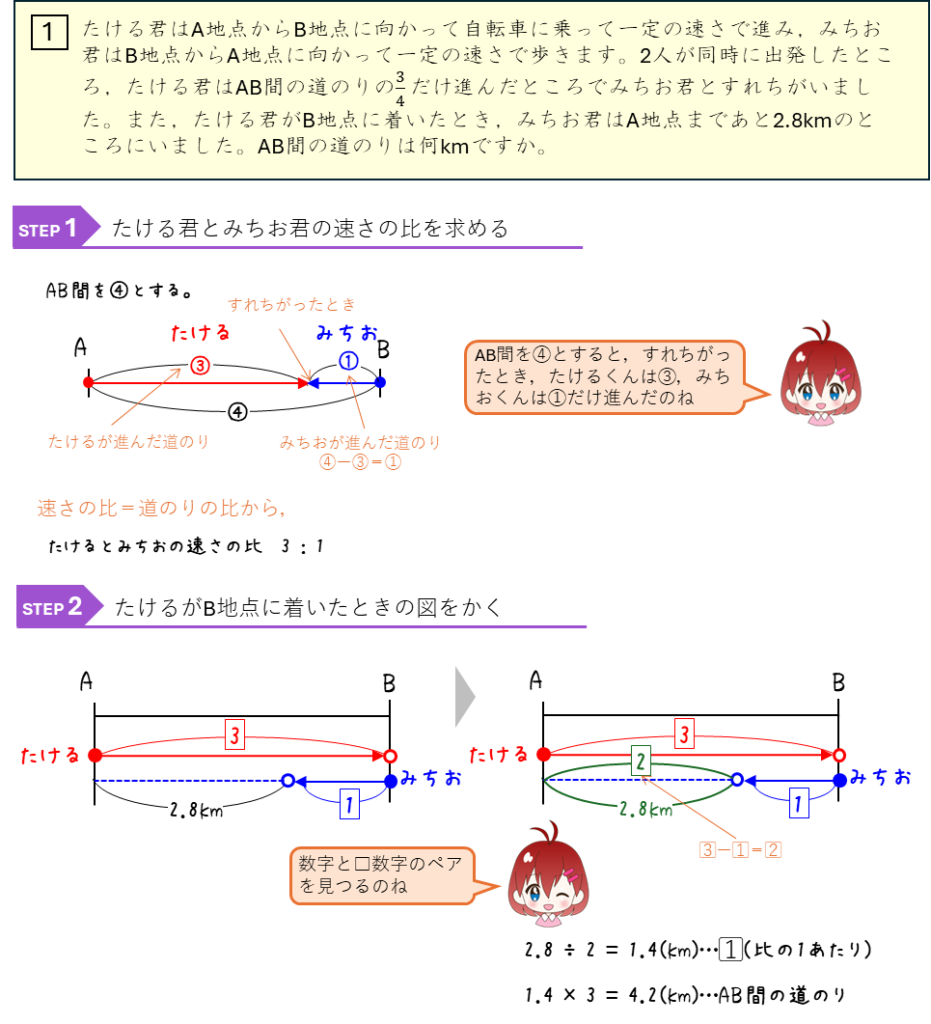
旅人算と比ー2人がすれちがう(すれちがったときの時間が分かる)
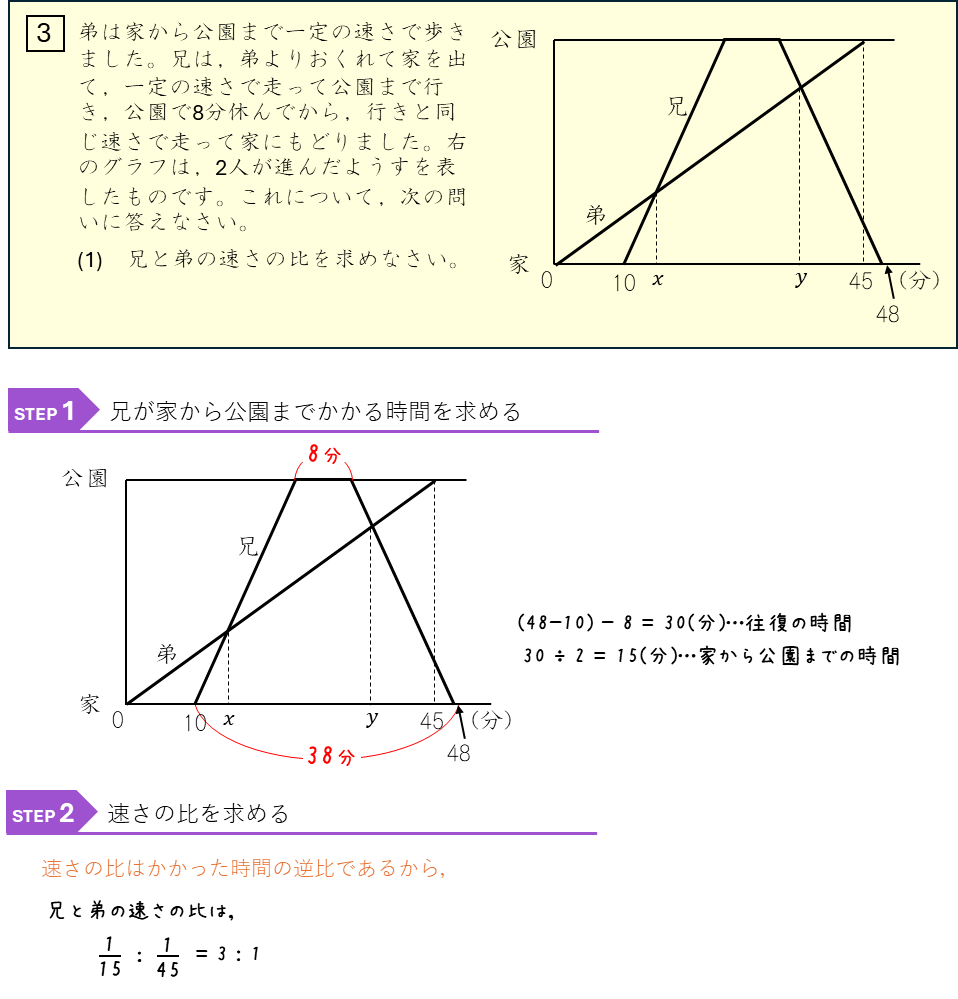
旅人算と比ー旅人算のグラフの三角形
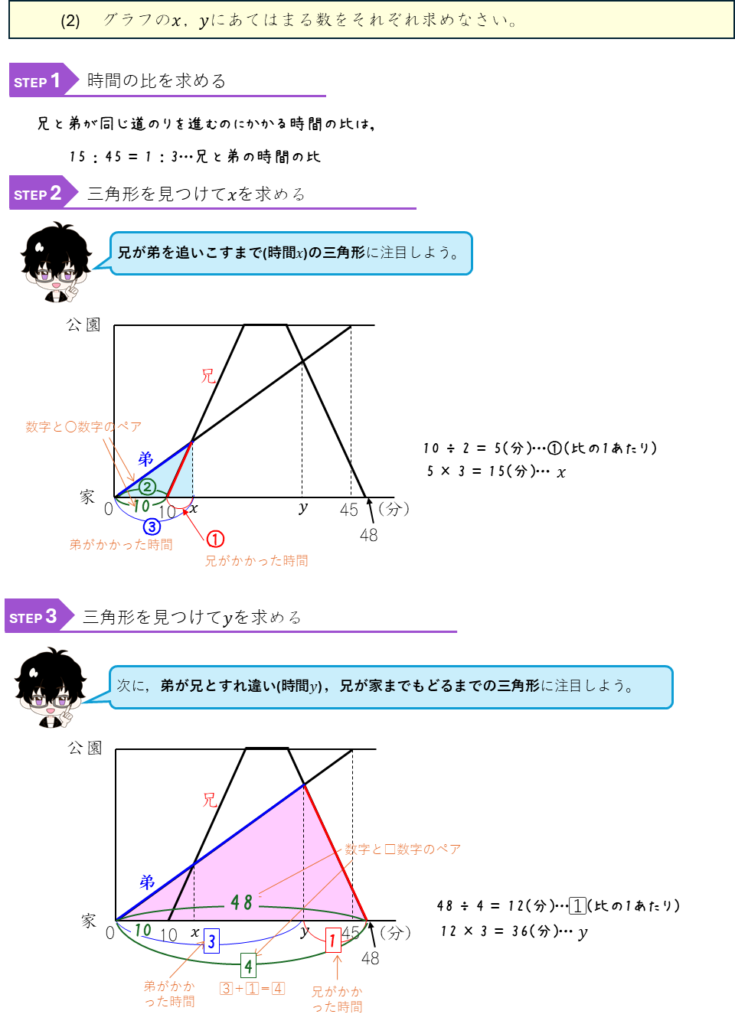
旅人算と比ーグラフから速さの比、道のりの比と差を求める
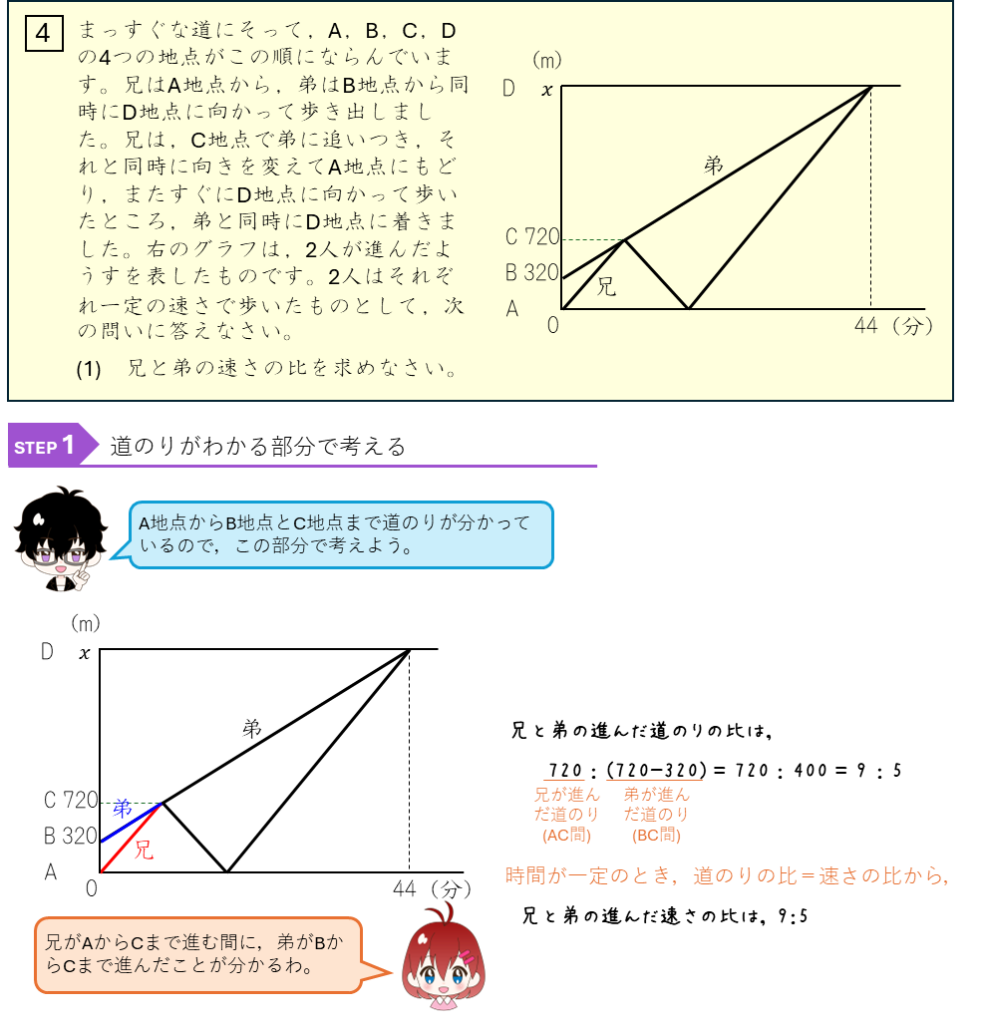
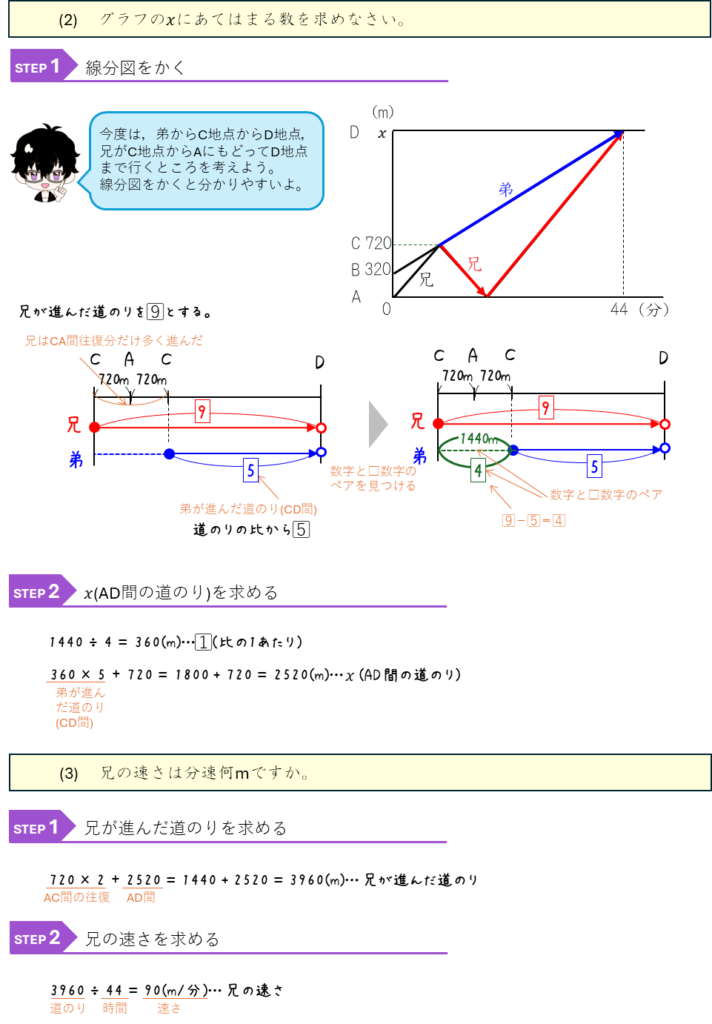
旅人算と比ー折り返しの旅人算
コメント