
今回は、「速さと比」についてを勉強していきます。割合と比を苦手にしている人には、少し難しいかもしれませんが、比を使って速さに関する問題を解いていきます。
ここでも、速さの3つ公式、
・速さ = きょり(道のり)÷時間
・きょり(道のり) = 速さ×時間
・時間 = きょり(道のり)÷速さ
が、基本なので、これがしっかり使いこなして解いていきましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
速さの比の公式
今回、新しく「速さの比」、「きょり(道のり)の比」、「時間の比」が出てきました。これら3つの比の関係は、速さの公式と同じになります。
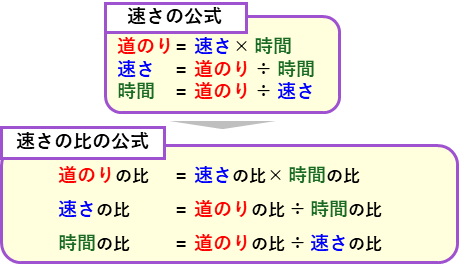
速さの公式がしっかり身についていれば、比に変えるだけですので、簡単に覚えられると思います。
どれか1つが一定のとき
速さ、道のり、時間のどれか1つが一定だった場合、3つの比の関係は次のようになります。

「道のりの比 = 速さの比× 時間の比」を思い浮かべれば、上の関係がイメージできると思います。
速さと比の問題の解き方
速さの比、道のりの比、時間の比を求める
問題文を読んで、そこから、速さの比、道のりの比、時間の比を求めるのが基本です。上の公式をしっかり身に付けましょう。
速さの比の計算になれる
速さの比の問題は、速さが速さの比に、道のりが道のりの比に、時間が時間の比に変わっただけと考えて、普通の速さと同じように計算できるかが、ポイントになります。時速20kmとか、30分とか実際の数字のかわりに、②とか、③とか、丸数字で比にあたる量を表すので、はじめはイメージしづらいのですが、問題を解いて、自然と計算できるようになりましょう。
分配算やつるかめ算として解く
比で表すことができたら、分配算やつるかめ算を使って解きましょう。分配算では、
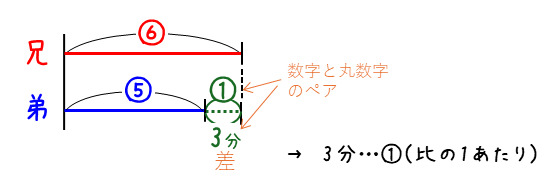
上の図のように、線分図をかいて、「数字と丸数字のペア」を見つけて、比の1あたりの量①を求めて解いていきます。
また、途中で速さが変わる問題は、「速さのつるかめ算」になります。
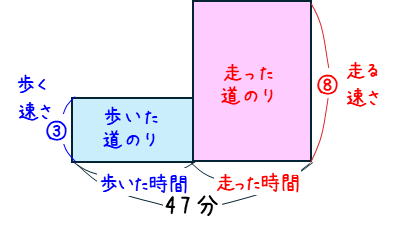
上の例では、速さが実際の数字ではなくて、③や⑧といった比にあたる量になりますが、普通の速さの計算と同じように解きましょう。
まとめカード
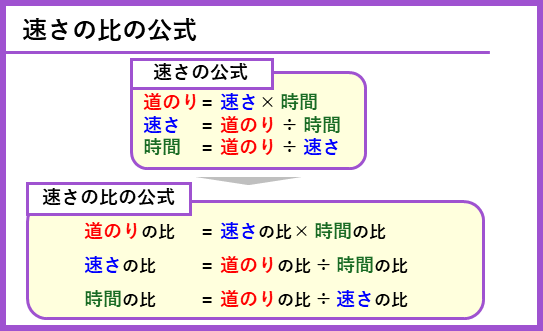

練習問題
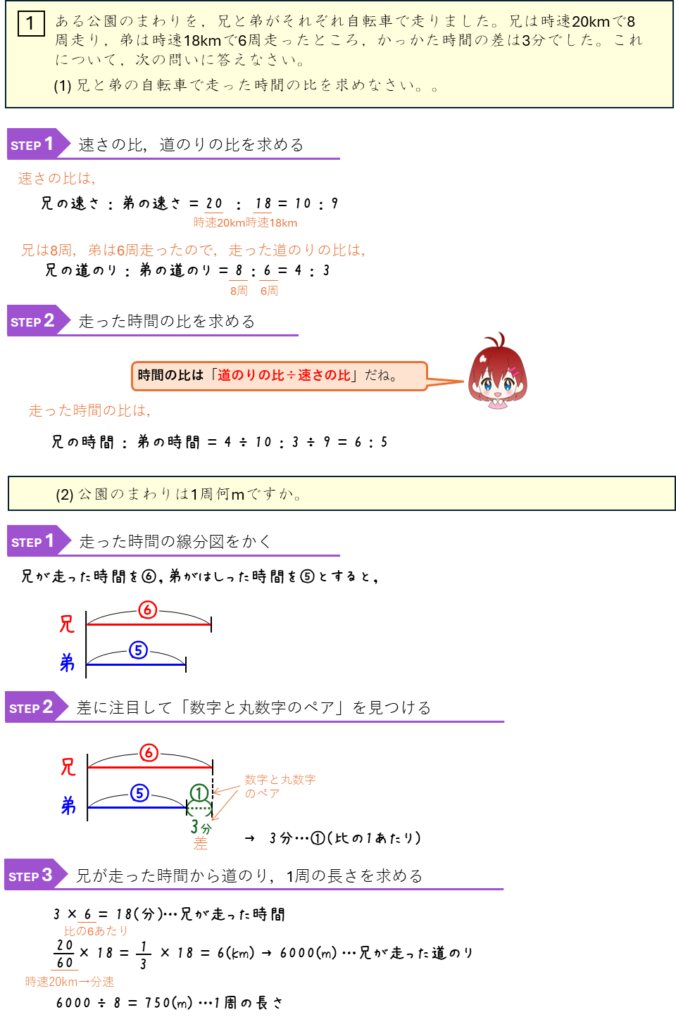
速さの比ー時間の比の分配算
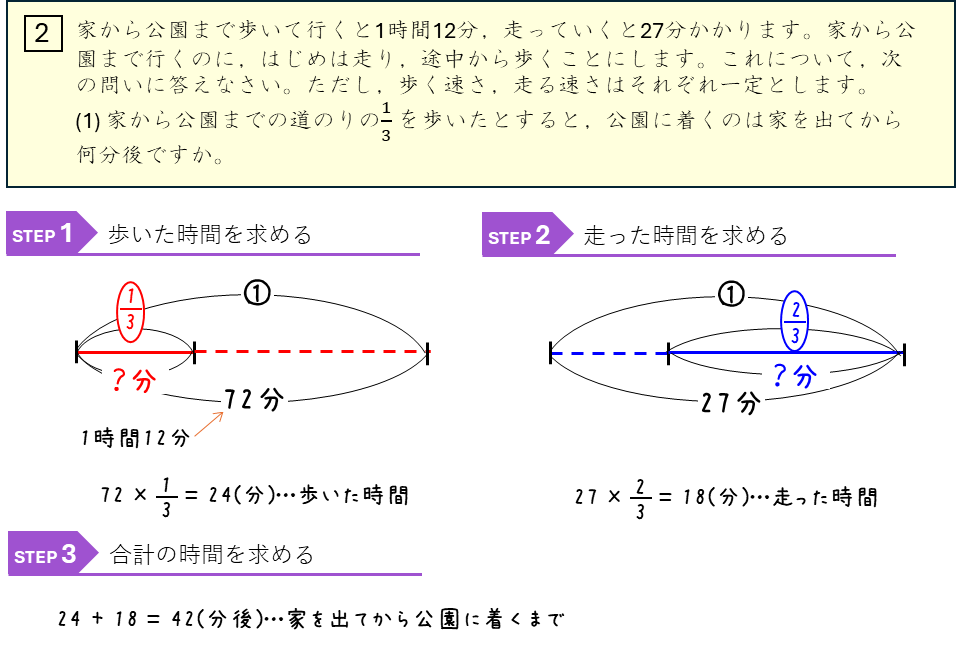
速さの比ー速さの比のつるかめ算
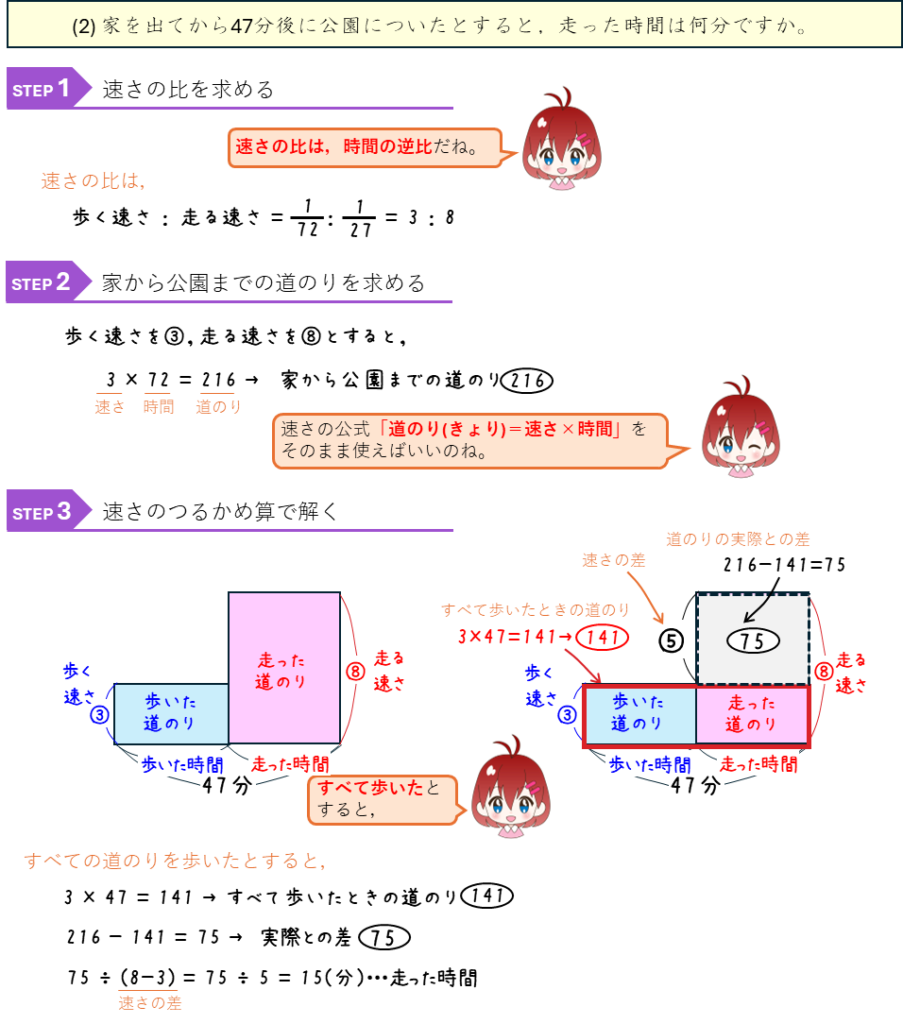
速さの比ー平均の速さ
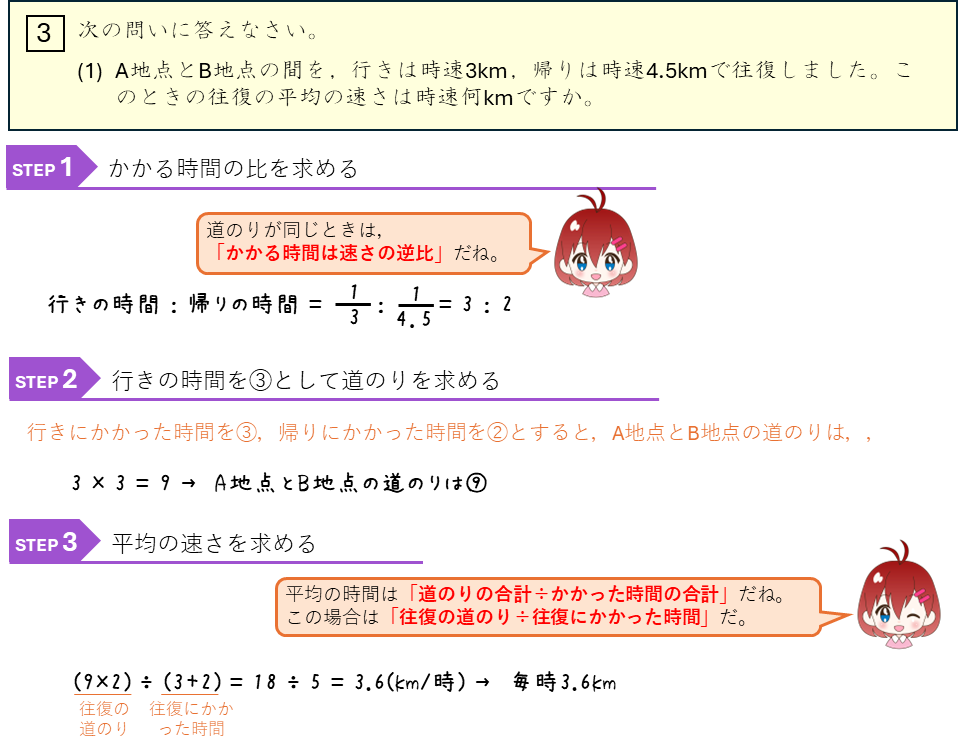

速さの比ー途中で速さが変わる
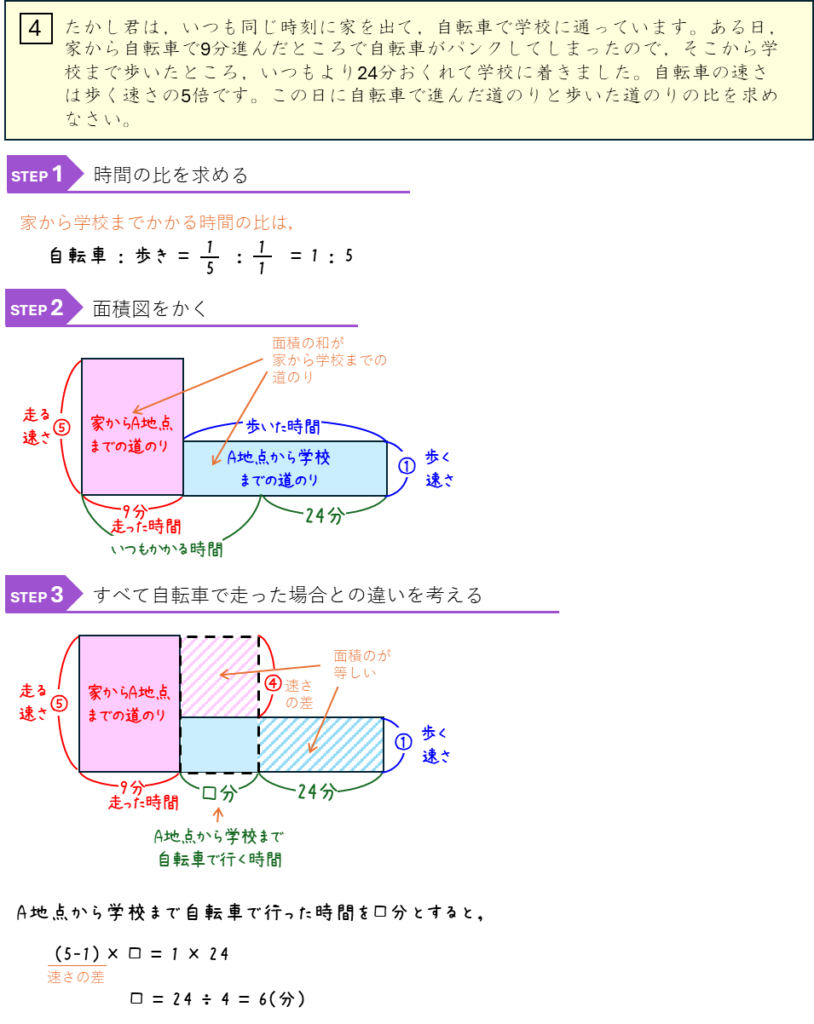

速さの比ー3人の短きょり走
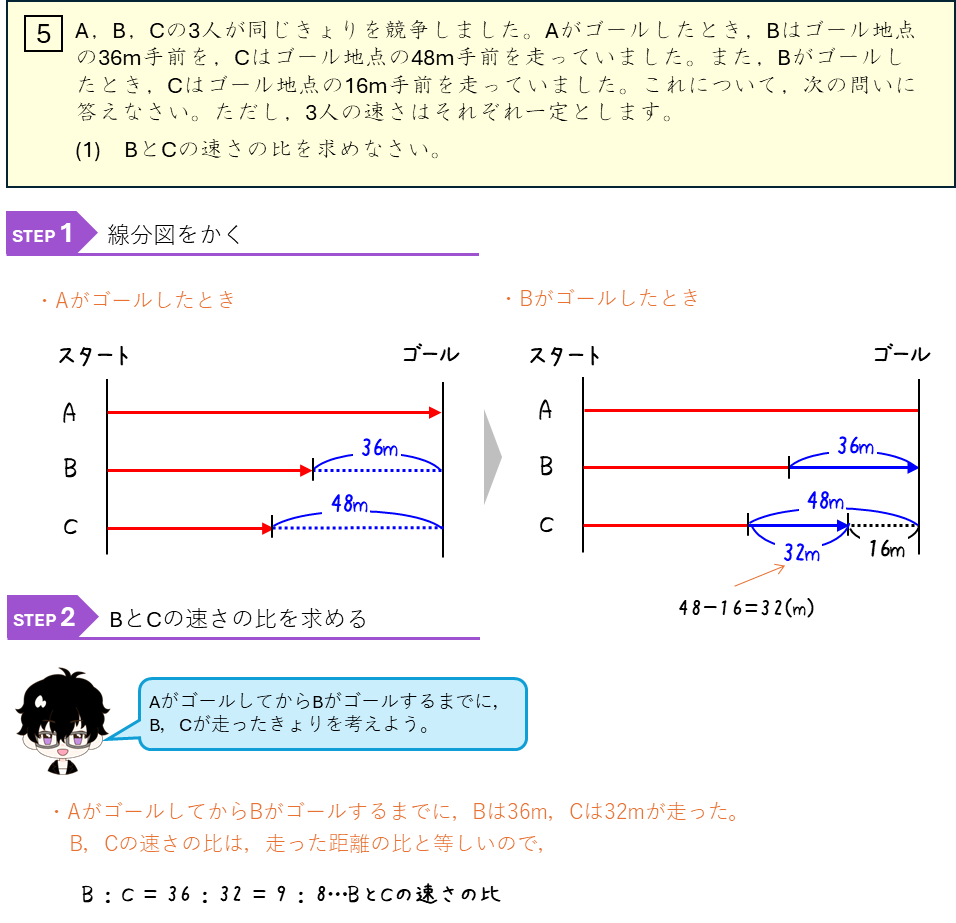
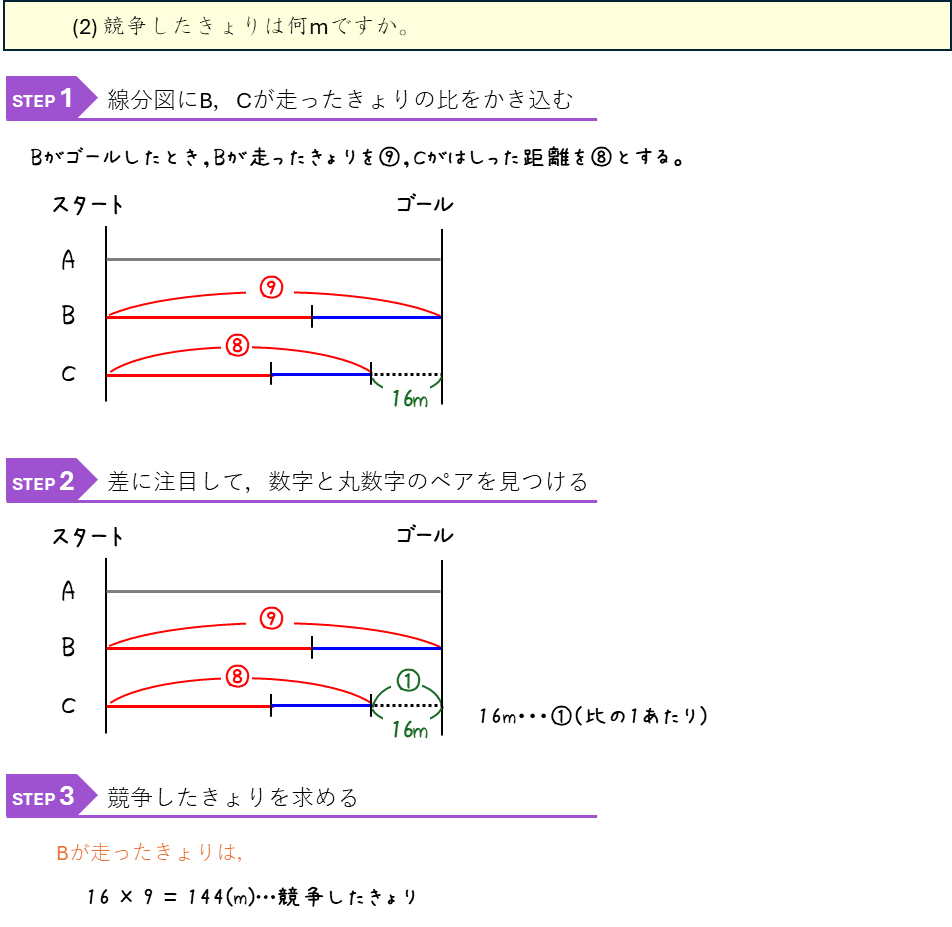
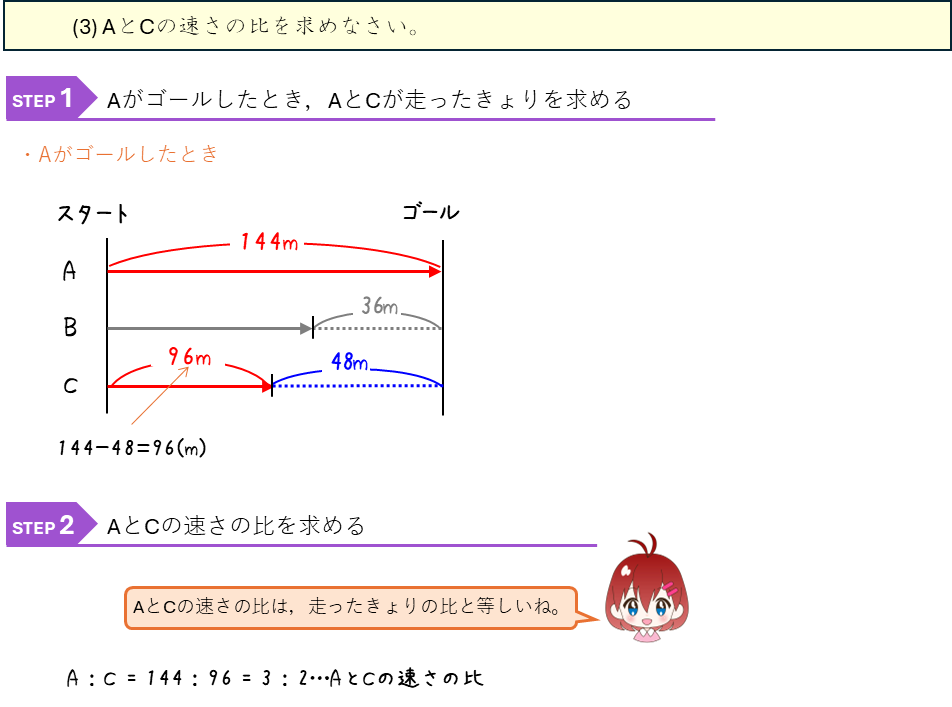
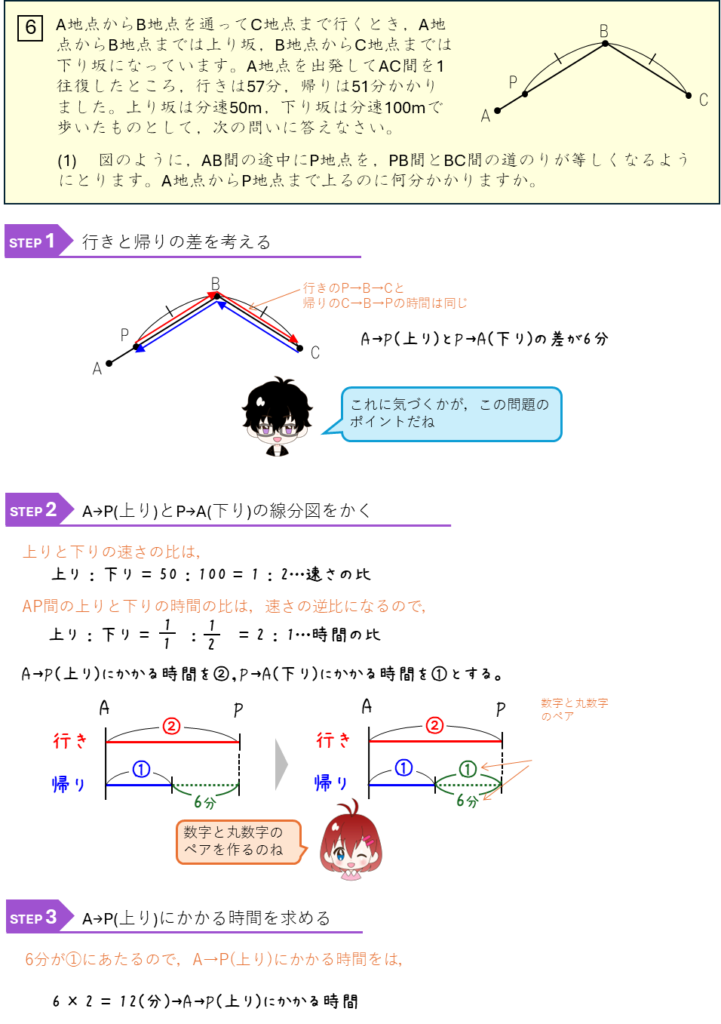
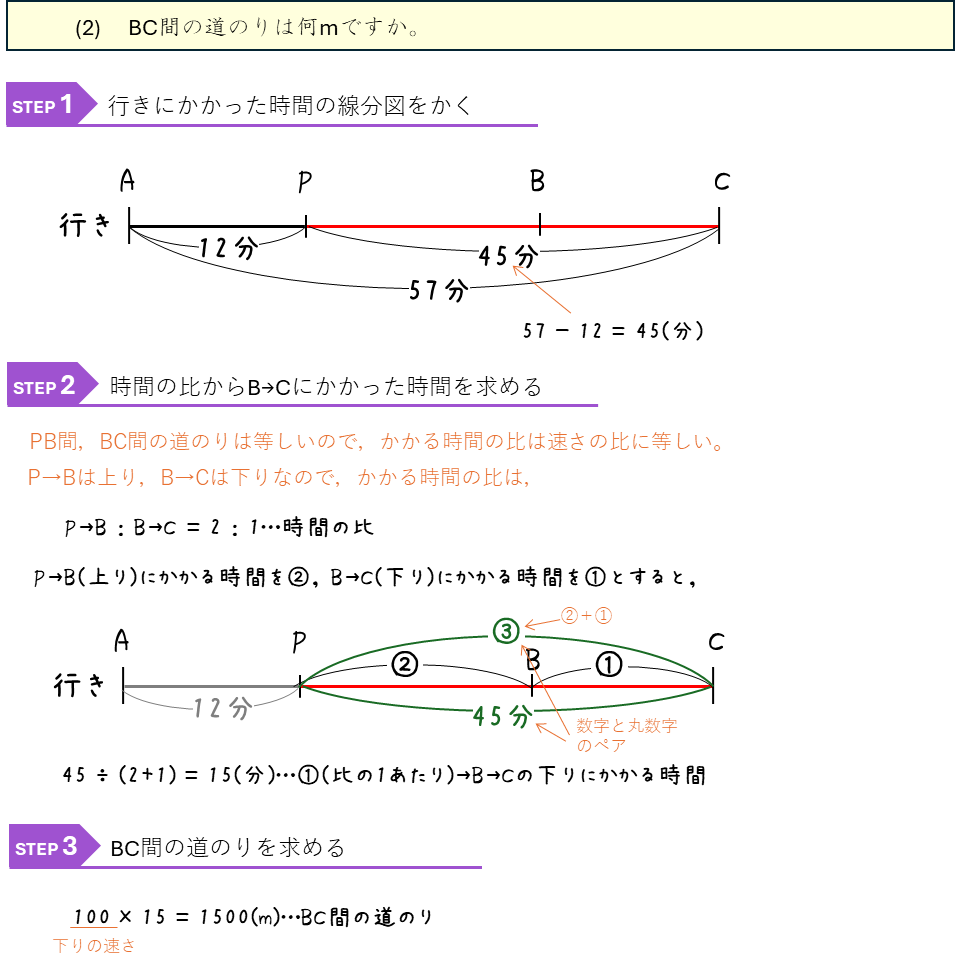
速さの比ー上り坂と下り坂の往復
コメント