
今回は、特殊算の「つるかめ算」と「年令算」のいろいろな応用問題を勉強していきます。
つるかめ算は、四年生のときに基本を勉強しました。それをベースに、
- 3つの量のつるかめ算
- じゃんけんゲーム
- 「いもづる算」(条件不足のつるかめ算)
などを、解いていきます。
また、「年令算」では、年令の差は一定というかくれた条件を使って解いていきます。線分図をかいて考えるのが基本ですが、倍数算として解いたり、難しい問題では、式を立ててから解くなど、色々な問題があります。
今回は、さまざまな応用問題が出てくるので大変ですが、解き方をしっかり理解していきましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
練習問題
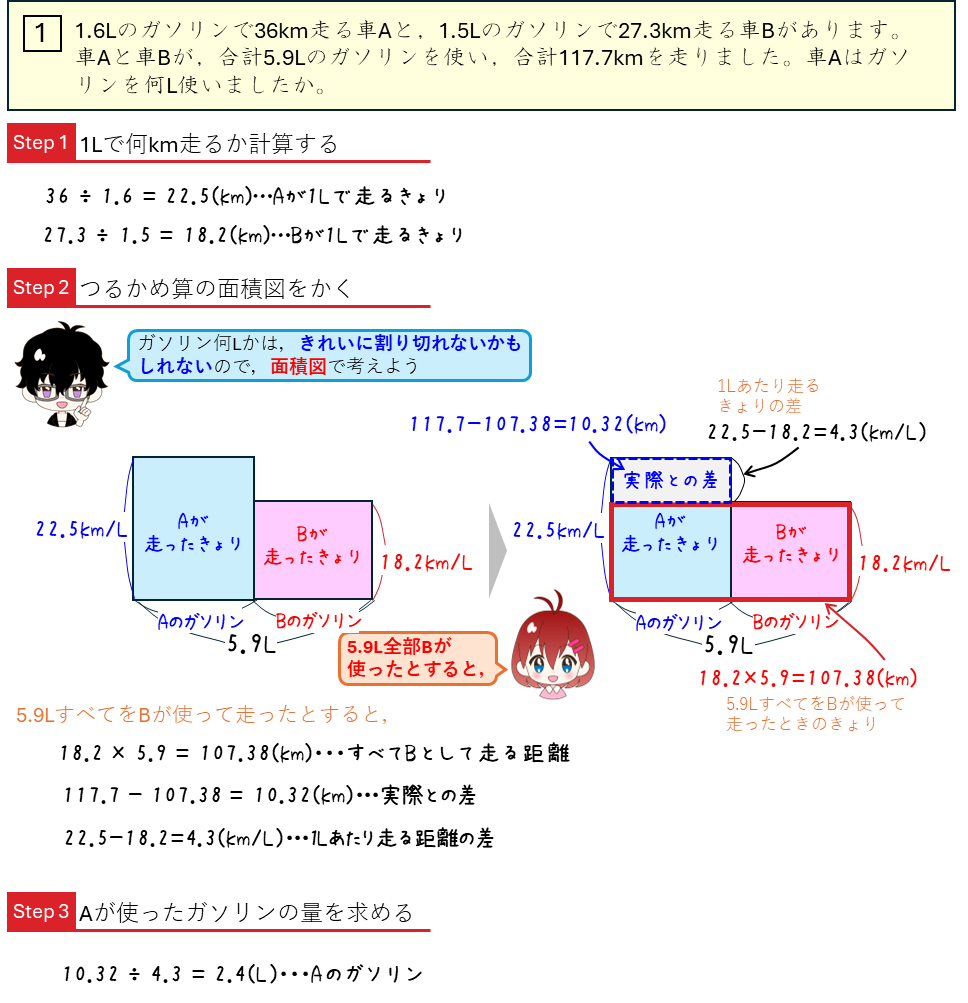
答えが小数になるつるかめ算

この問題は、車Aと車Bの1Lあたり走るきょり、2台で走ったときのガソリンの合計、走った距離の合計から、車Aの使ったガソリンの量を求める問題です。ガソリンの量は、1個、2個、、、、や、1人、2人、、、、のようにかならず整数になるわけではなく、小数や分数になるかもしれません。図で解く場合は、面積図を使って解きましょう。
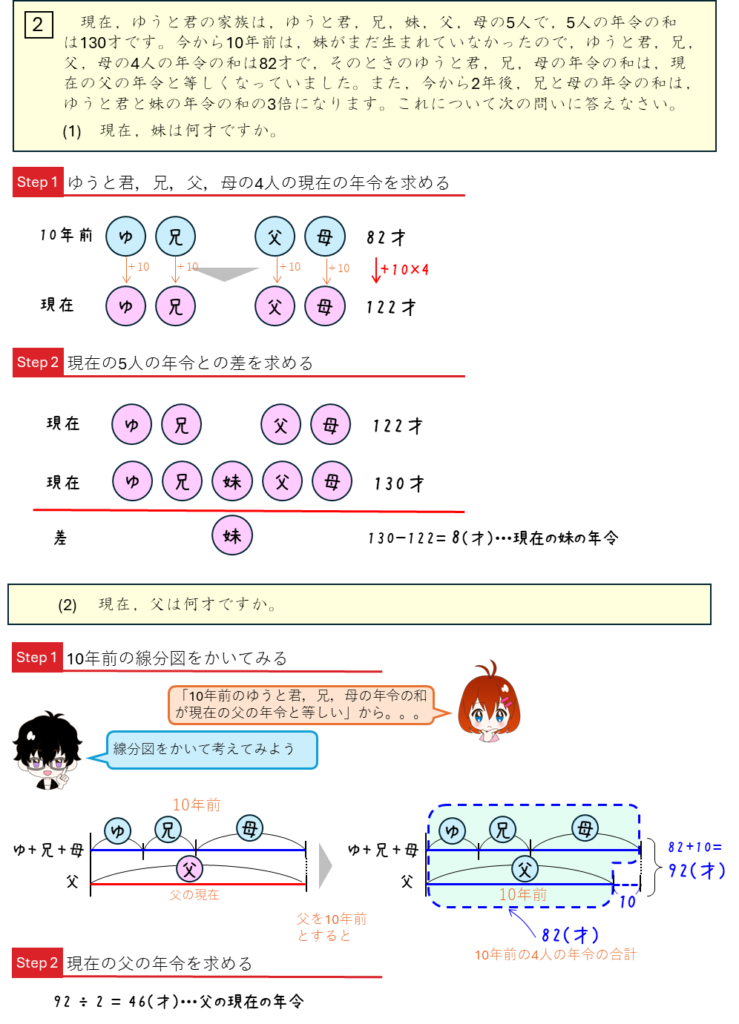
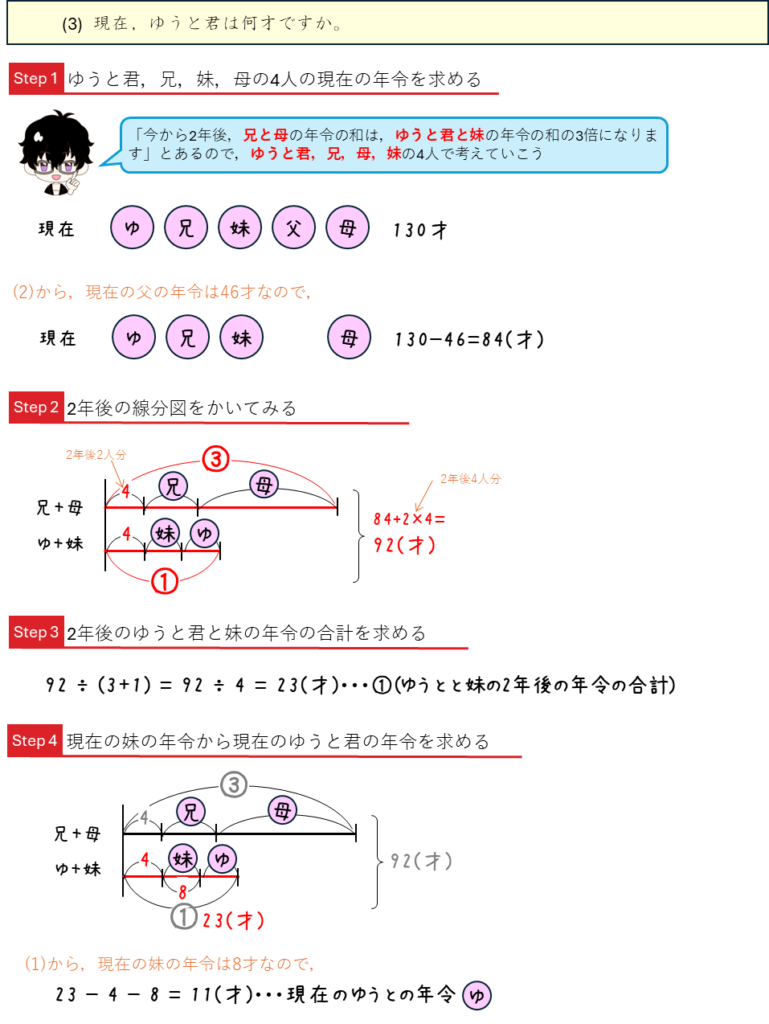
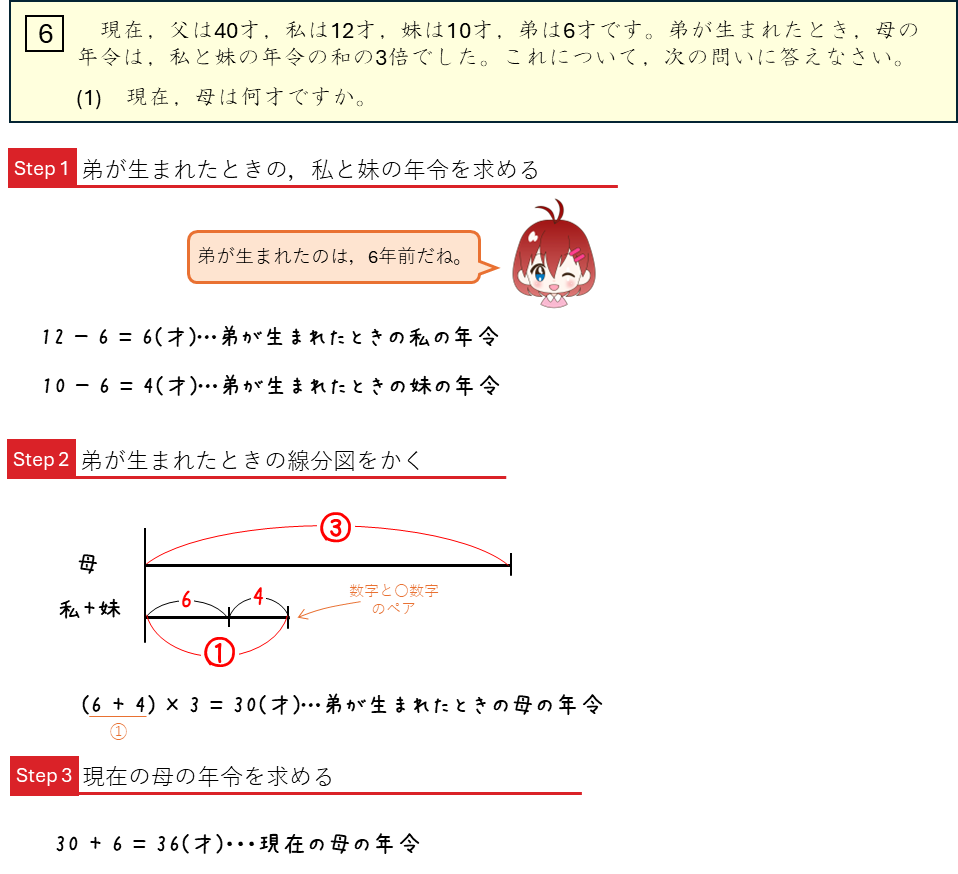
年令算ー家族の年令の和
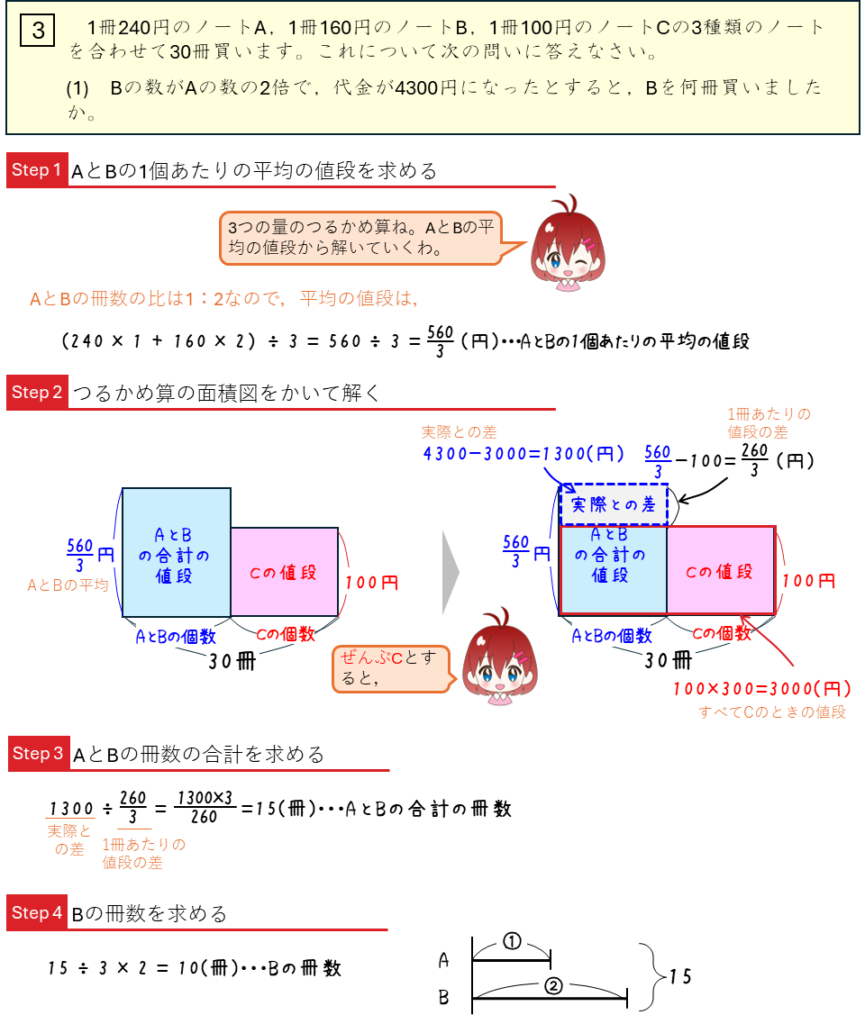
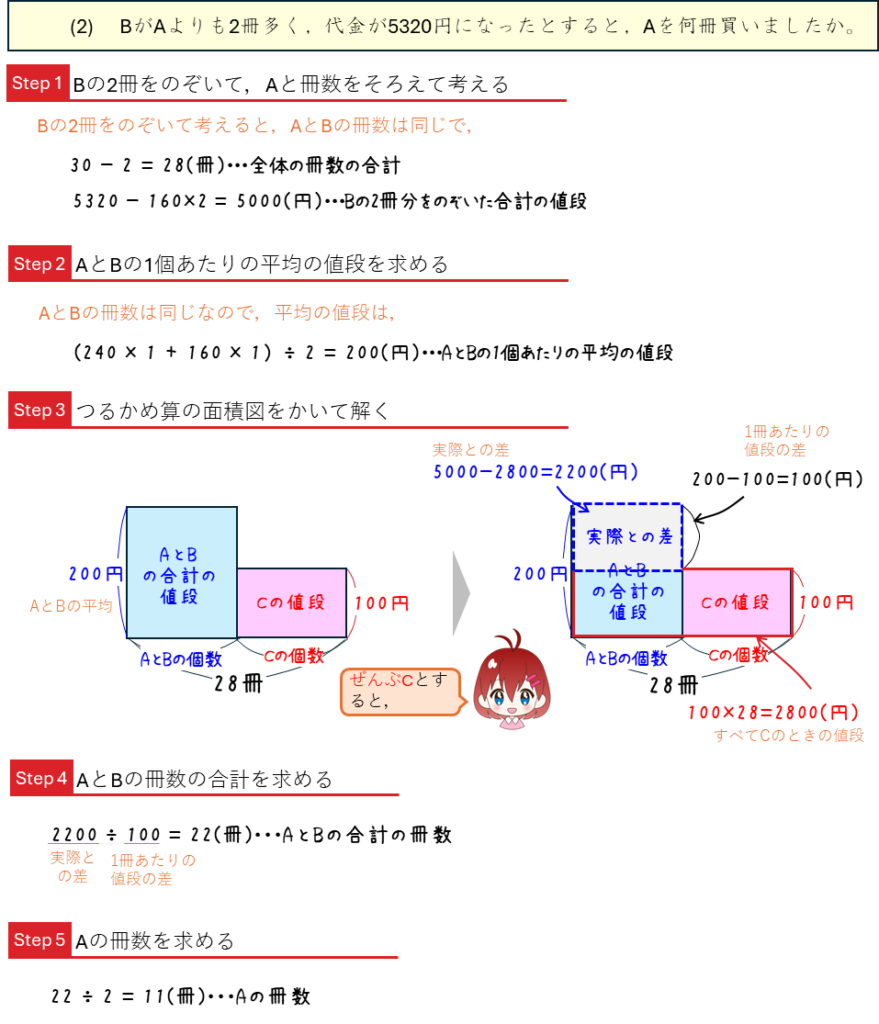
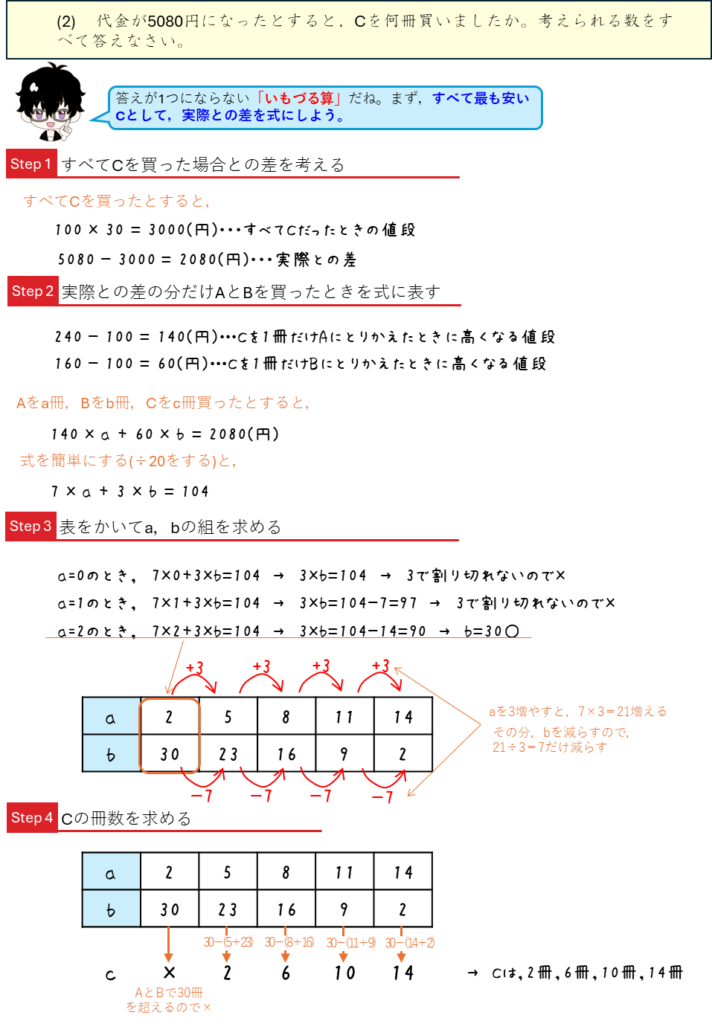
3量のつるかめ算といもづる算
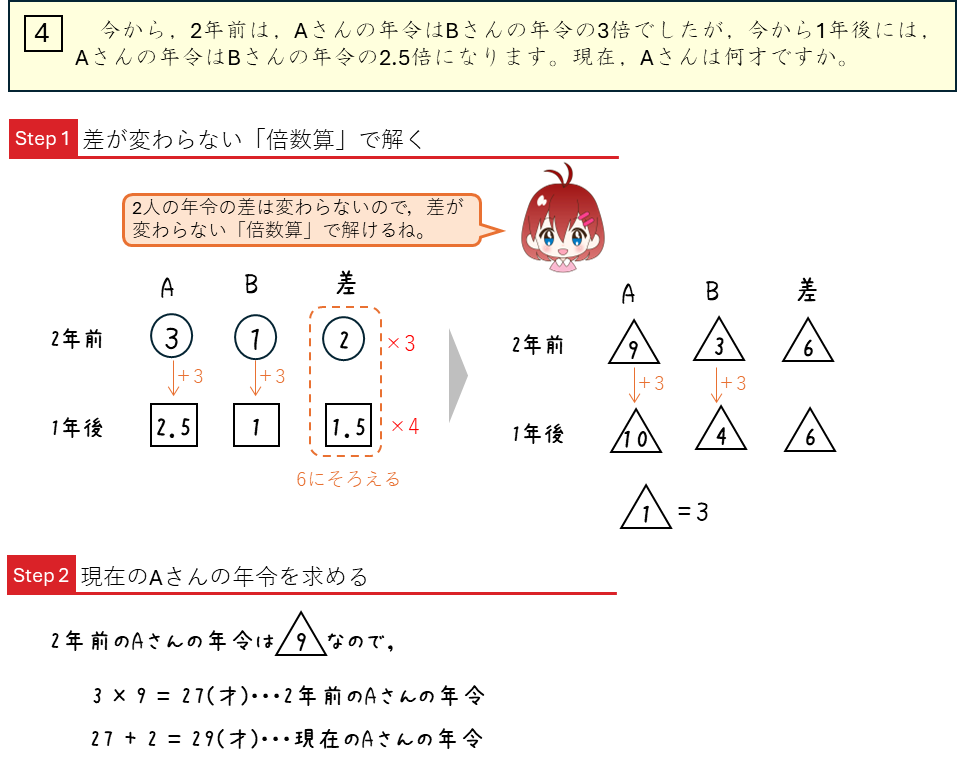
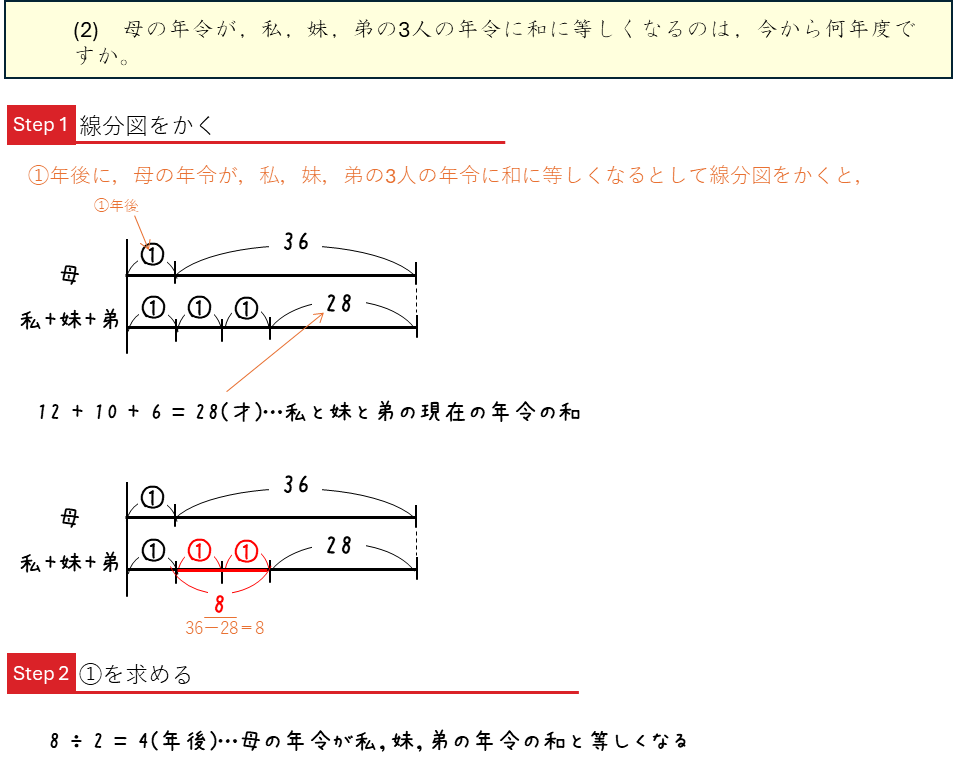
年令算ー差が変わらない「倍数算」で解く
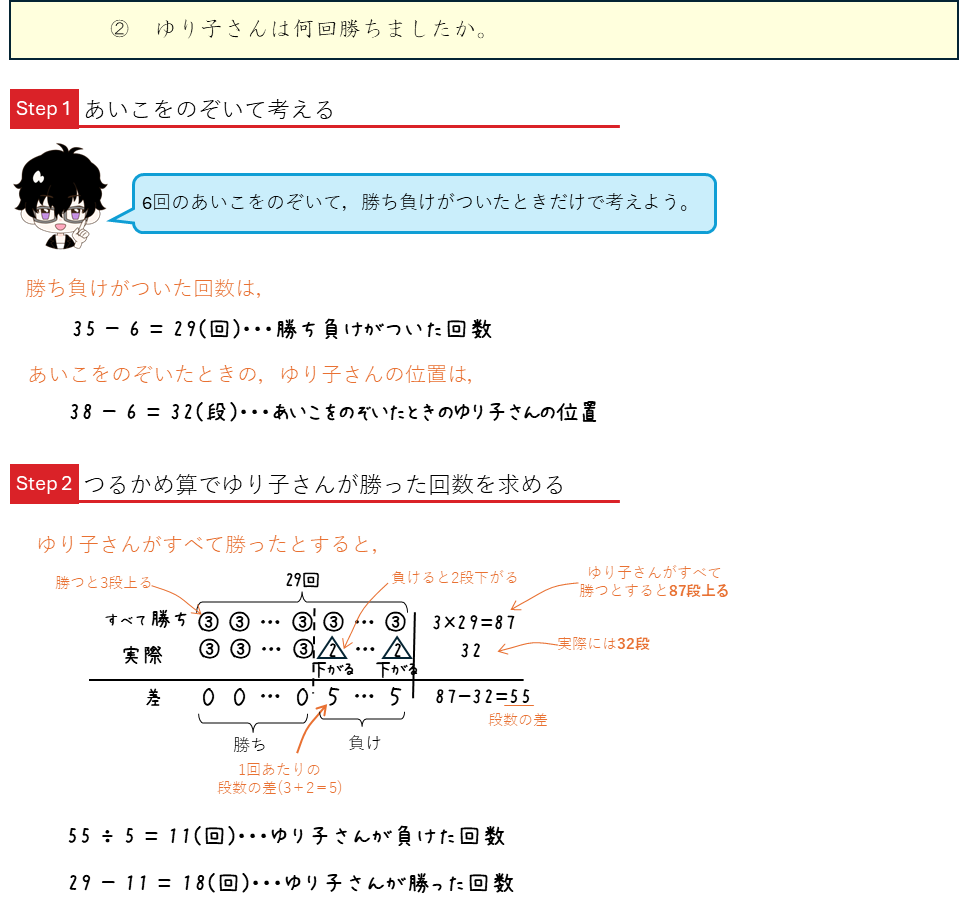
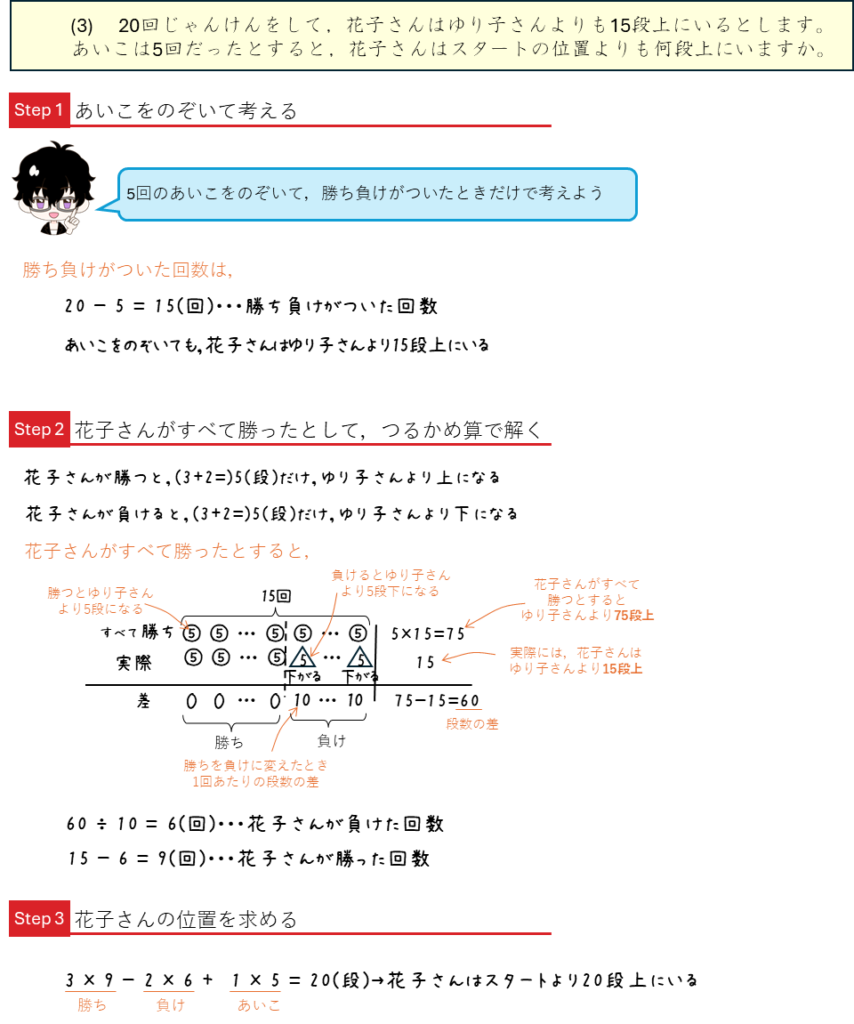
つるかめ算ーじゃんけんゲーム

年令算ー父と母の年令の和が3人の子どもの年令の和の2倍


コメント