
前回に続いて、平面図形と比に関するものです。今回は、辺の比と面積比について、夏期講習で学習した「底辺の比と面積比」を発展させた問題を解いていきます。
夏期講習では、「双子山型」と呼んだ高さが同じ三角形の面積比が出てきましたが、今回は、共通の角を持つ三角形や、2つの三角形の内角の和が180度になる三角形などが出てきます。底辺も高さもちがうので少し難しくなりますが、ポイントを押さえてしっかり理解しましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
解説
面積比ー高さが等しい(復習)
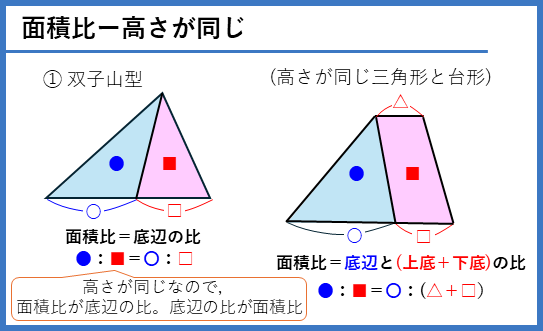
面積比ー底辺の比と高さの比
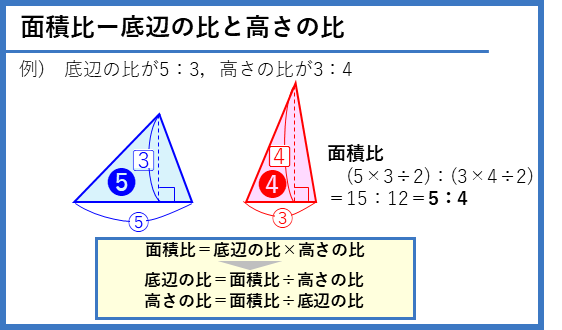
底辺の比と高さの比が分かっているとき、面積の比は、底辺の比と高さの比の積で求められます。また、底辺の比は(面積比÷高さの比)、高さの比は(面積比÷底辺の比)となります。面積の公式と対応して考えることで、楽に覚えられると思います。
面積比ー底辺も高さも違う
共通な角を持つ三角形や、角度が等しい三角形では、
面積の比は、共通の角をはさむ2辺の積の比
になります。それぞれが底辺、高さに対応していると考えて、面積なのでそれらの積になると考えればよいです。また、2つの三角形の1組の内角の和が180度となる場合も同じです。
代表的な形として次の3つがあります。「A(エース)型」、「チョウチョ型」、「カブト型」として、問題の図形の中から見つけることができるようにしましょう。
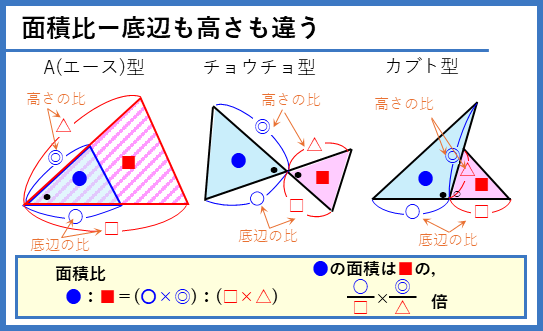
面積比の式は、式だけ見ると分かりづらいですが、次の例の通り、2辺を底辺と高さに対応させて、面積なのでかけ合わせると考えると良く理解できると思います(比なので、三角形の面積の式の÷2は省略できます)。問題によって、面積比の考え方の方が分かりやすいものと、割合の考え方の方が分かりやすいものがあるので、両方の考え方を理解しましょう。
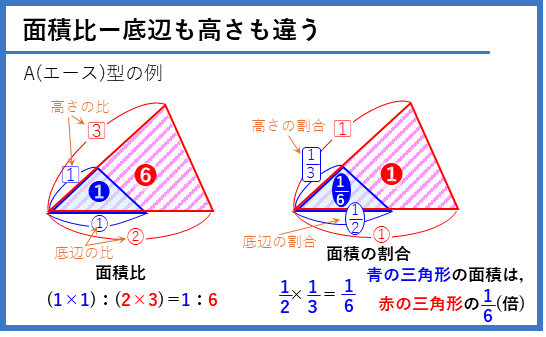
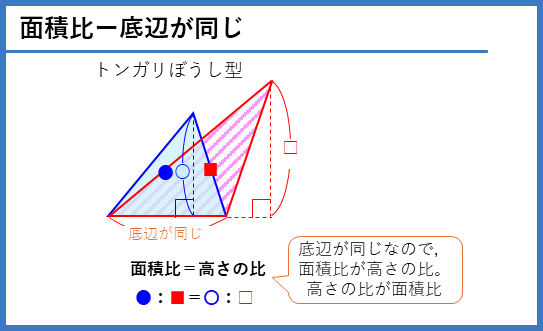
面積比ー底辺が同じ
練習問題では、底辺が同じ三角形の面積比に関する問題がでてきます。底辺が同じなので、
面積比=高さの比
となります。練習問題では下の図の形が出てきます。これも問題の図形から見つけ出せるようにしましょう。
底辺が同じとして考えるタイプの残りは、「第8回 平面図形と比ーまとめと応用ー」で勉強します。
練習問題
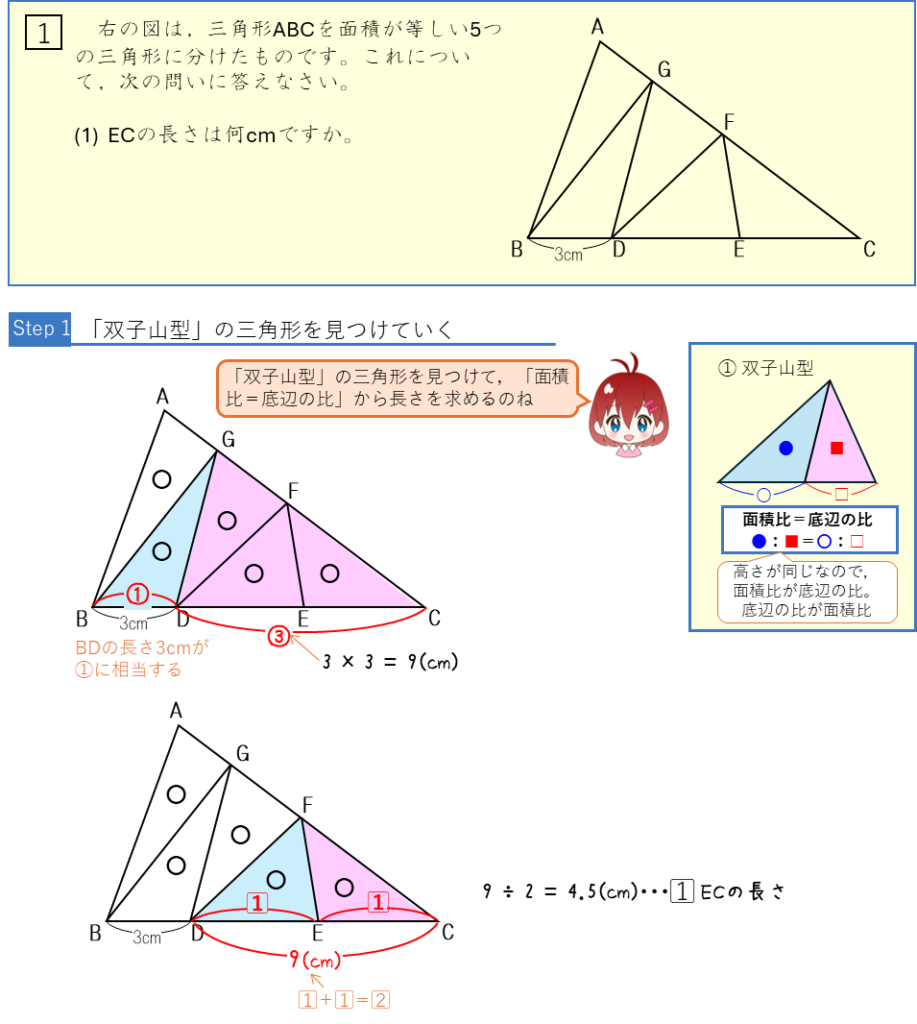
ギザギザ三角形:面積比ー面積比から長さや比を求める
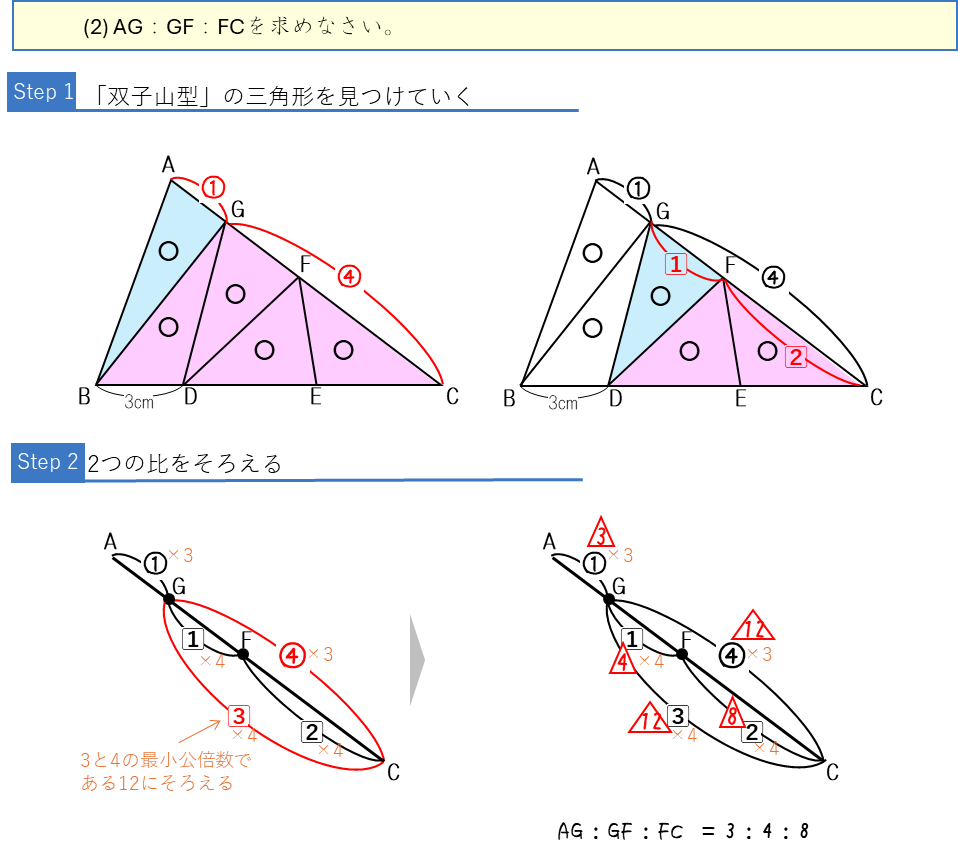
面積比ー辺の比から面積を求める
面積比ー面積比から辺の比を求める
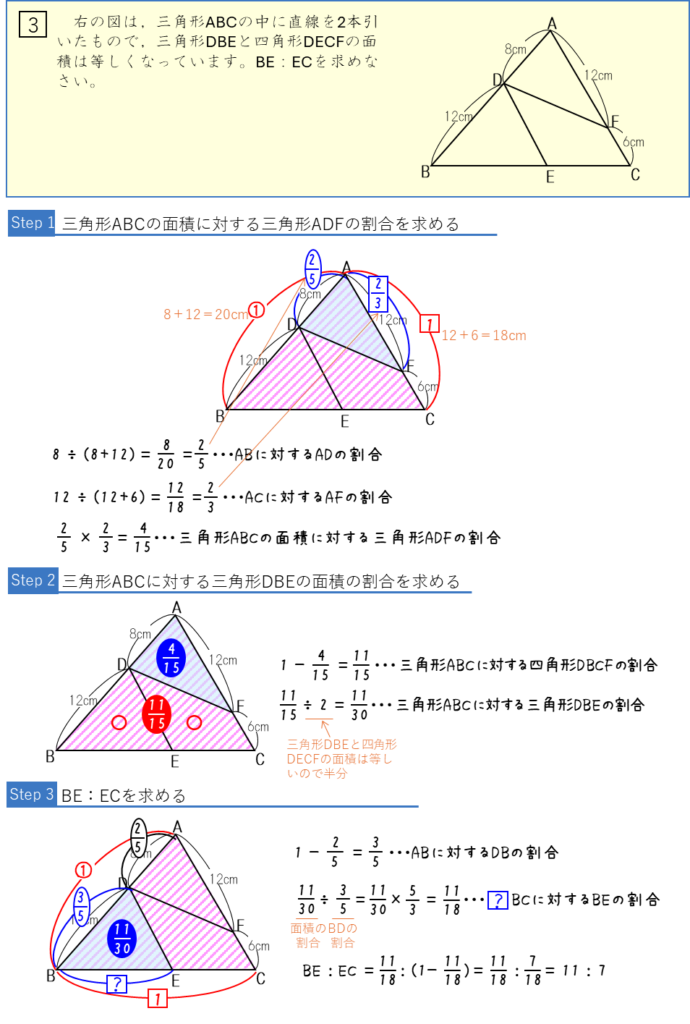
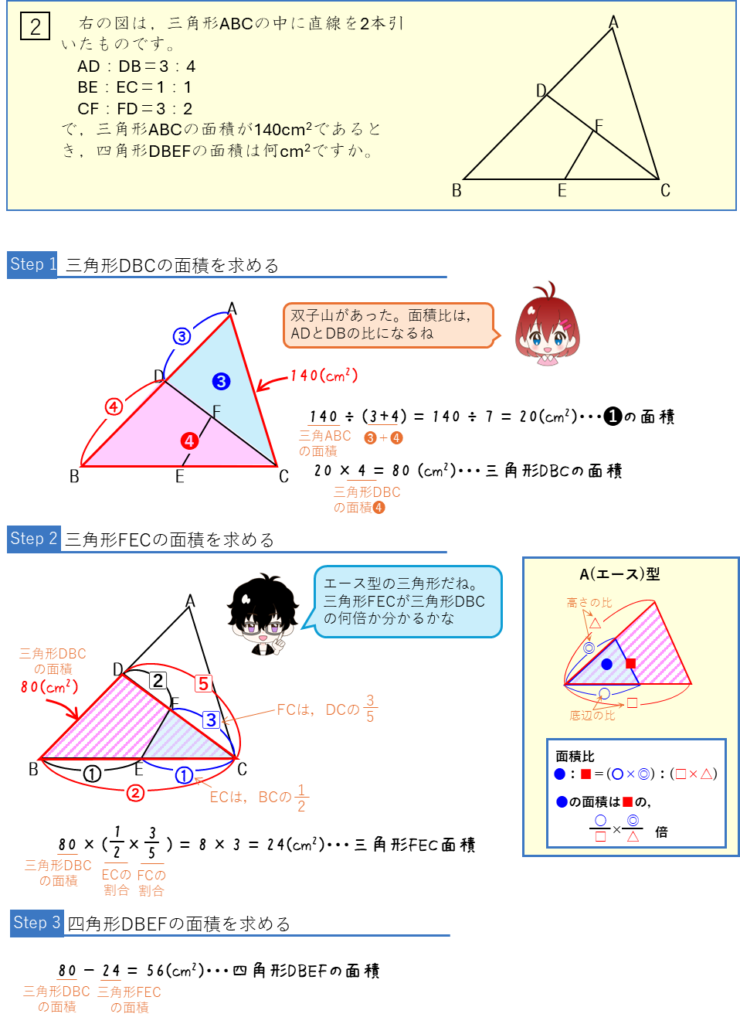
三角形の中の三角形:面積比ー面積から辺の比・辺の比から面積を求める
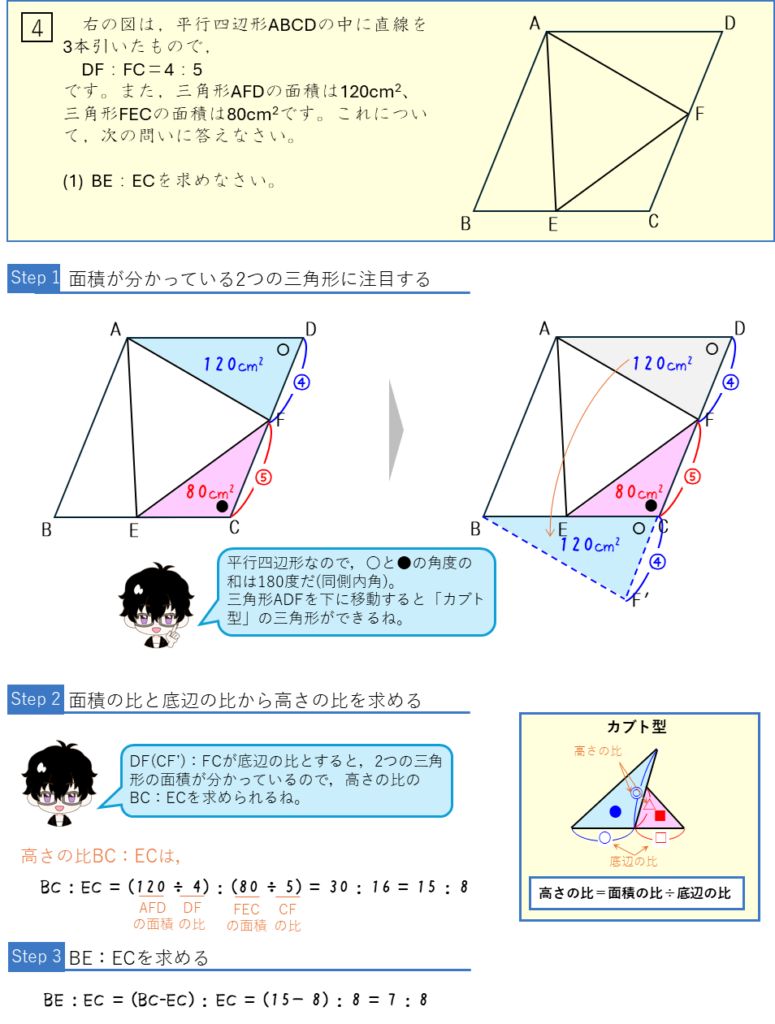
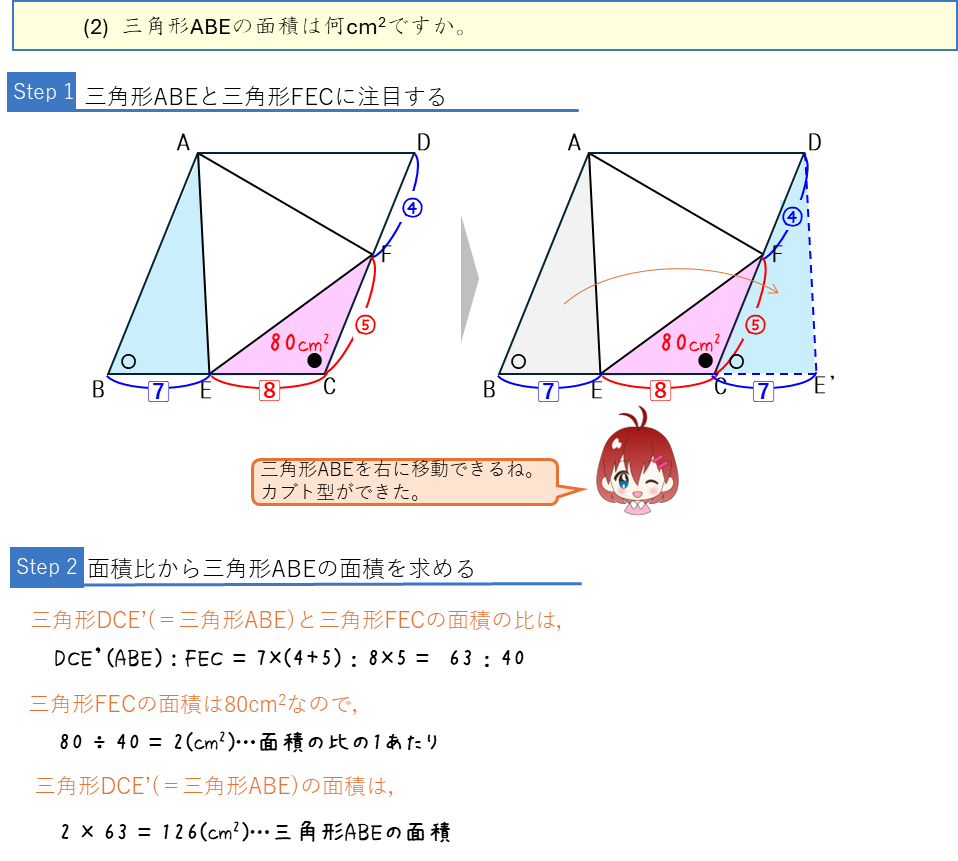
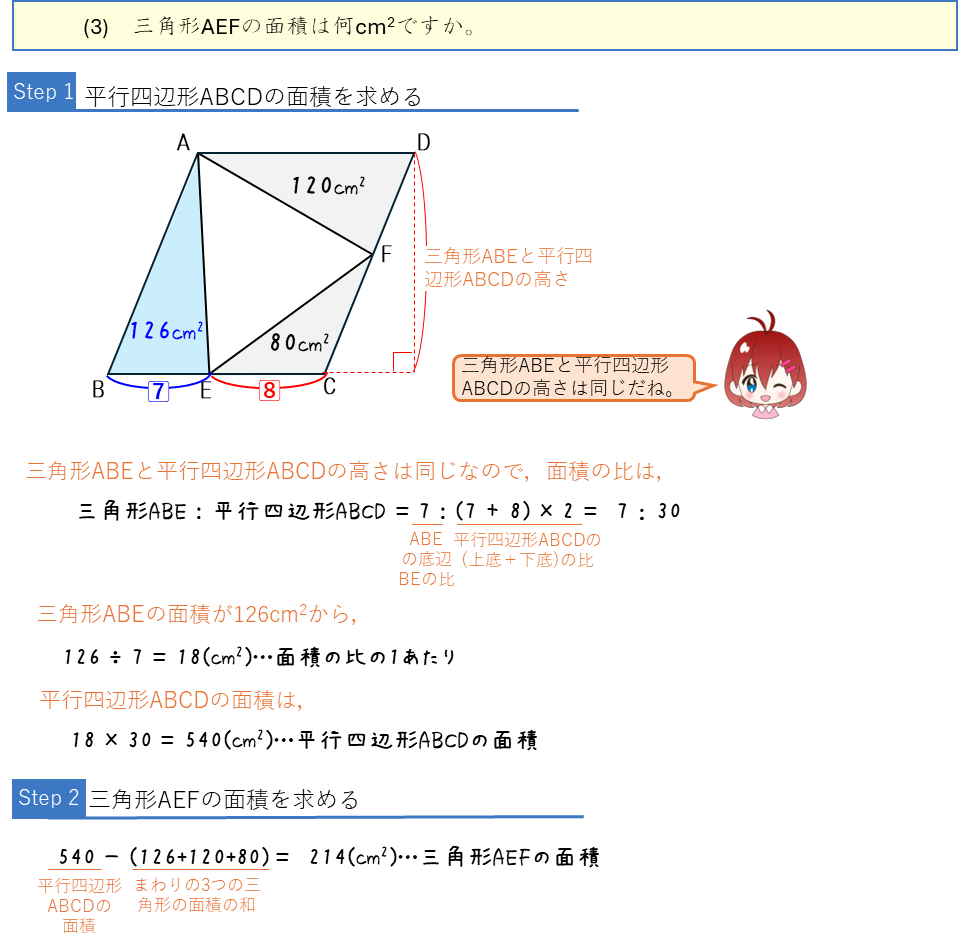
面積比ー面積から辺の比を求める・辺の比から面積を求める
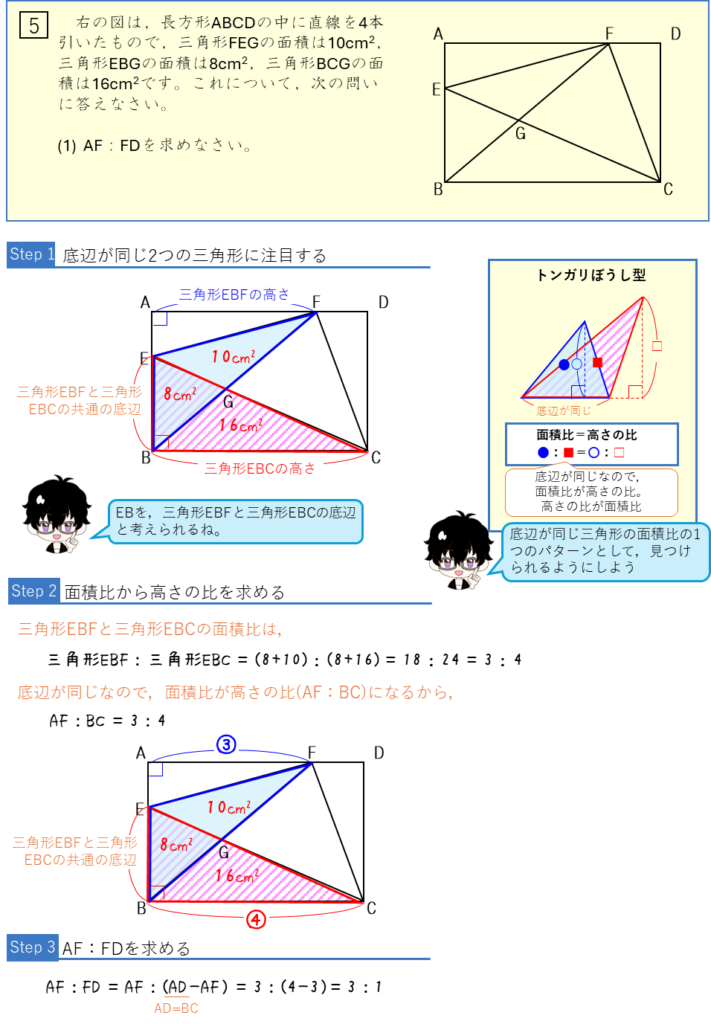
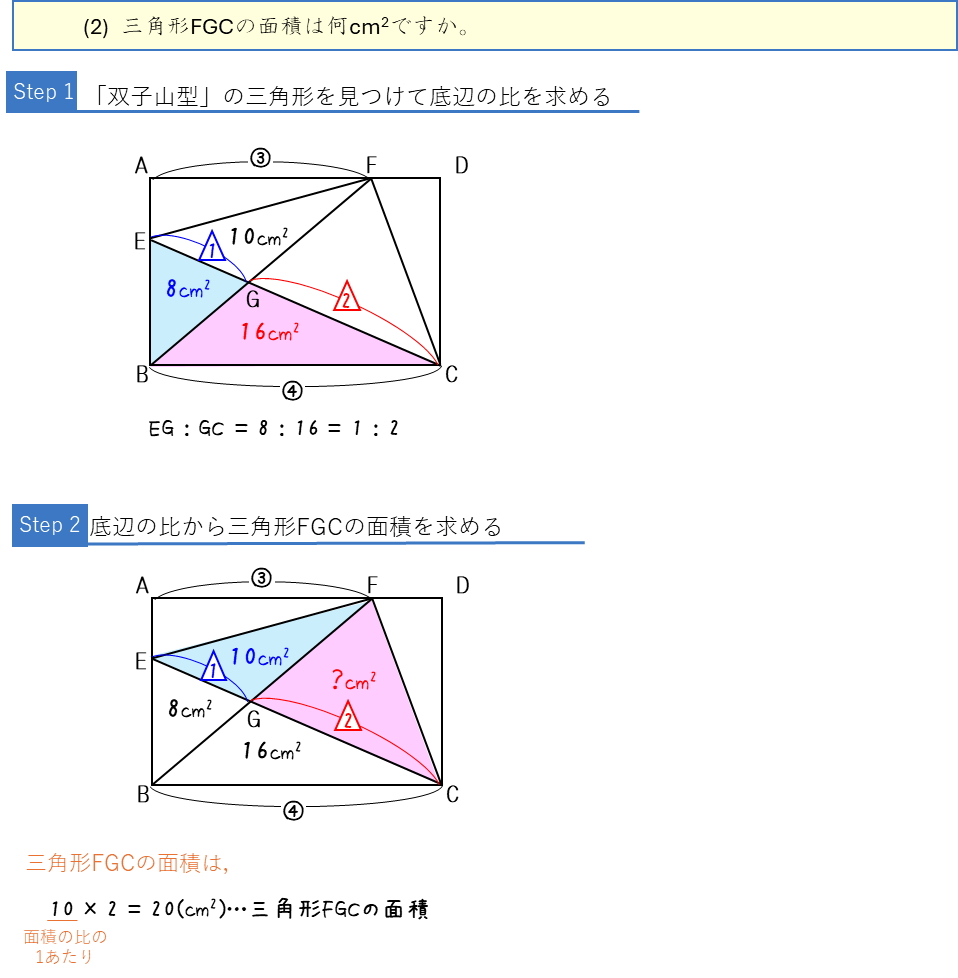
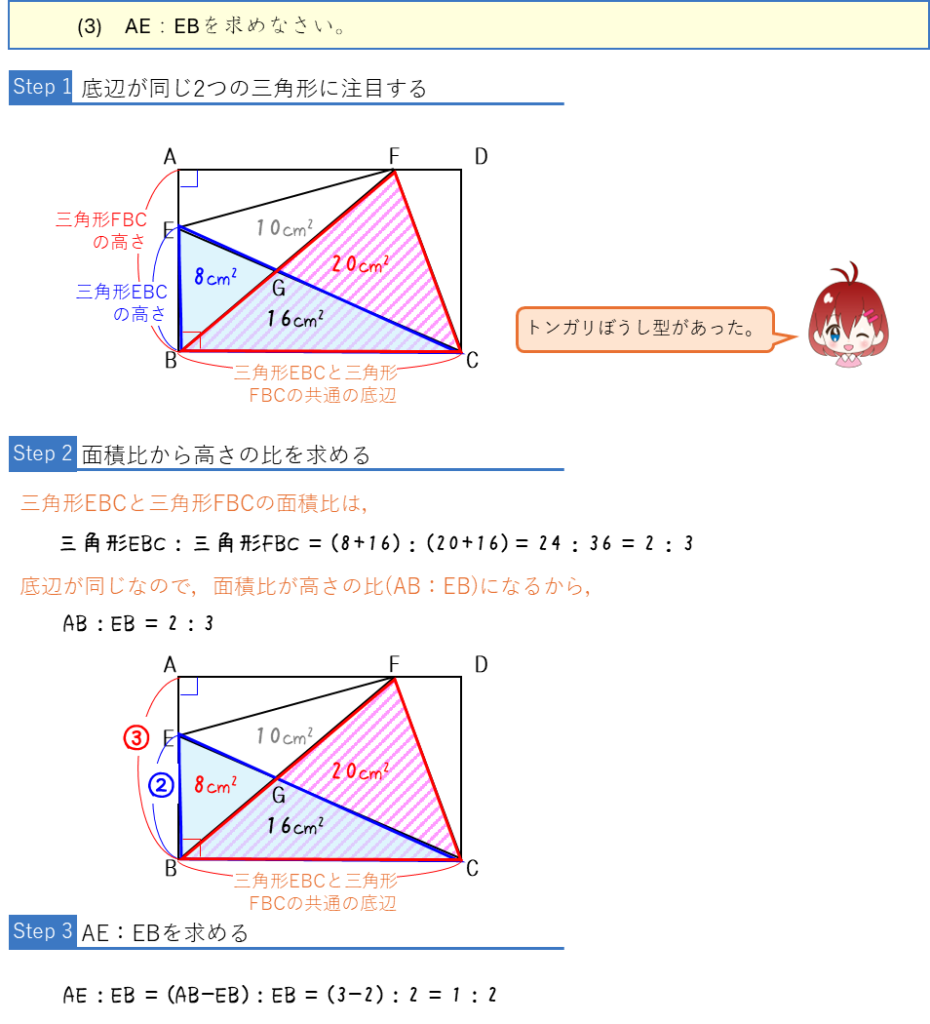
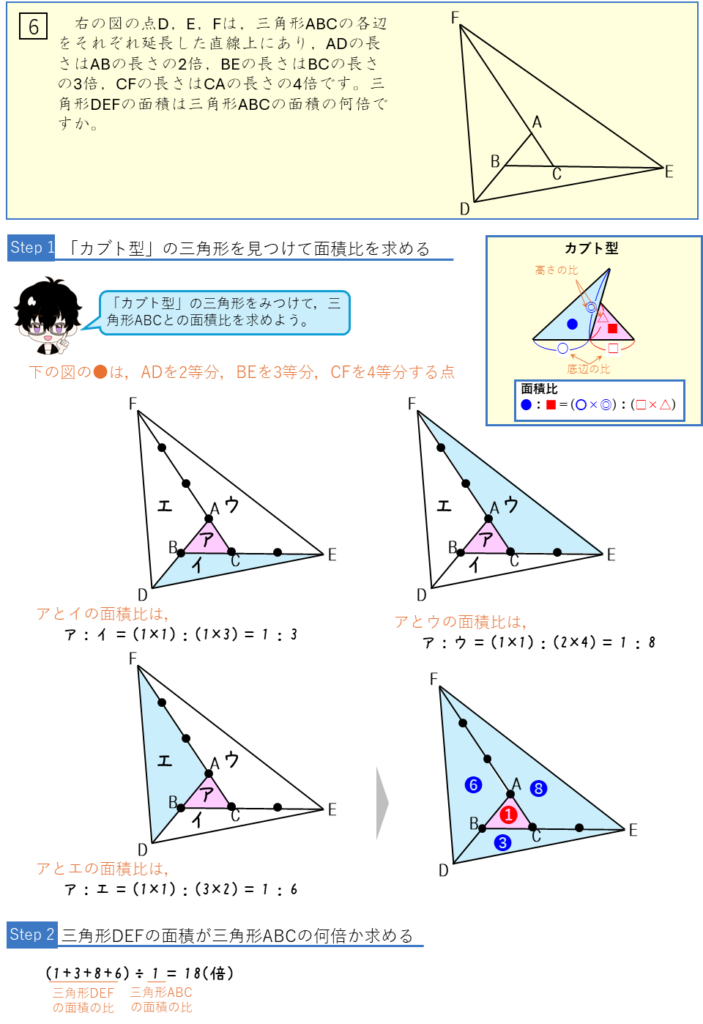
三角形の中の三角形:面積比ー辺の比から面積の比を求める

コメント