
今回の単元は、「水深の変化と比」です。「水量の変化」や「物体をしずめる問題」を今まで学びましたが、今回は、比を使った問題が出てきます。
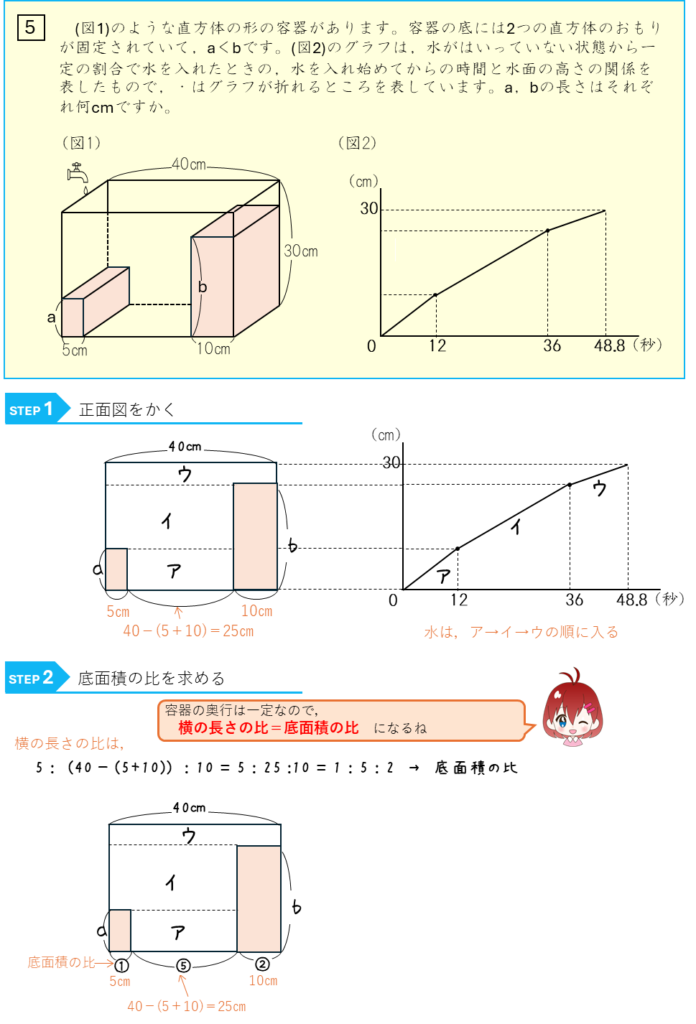
水量変化では、「正面図」をかいて解きます。正面図の横は底面積、たてが水深(水面の高さ)、そして、面積が体積とするのが基本です。比を使う問題では、底面積の比、水深の比、体積の比に変えて考えますが、本質的なところは同じです。
水の量については、
入る水の量(容器の体積)=単位時間あたり入る水の量×時間
という式になります。
一定の割合で水を入れる場合には、
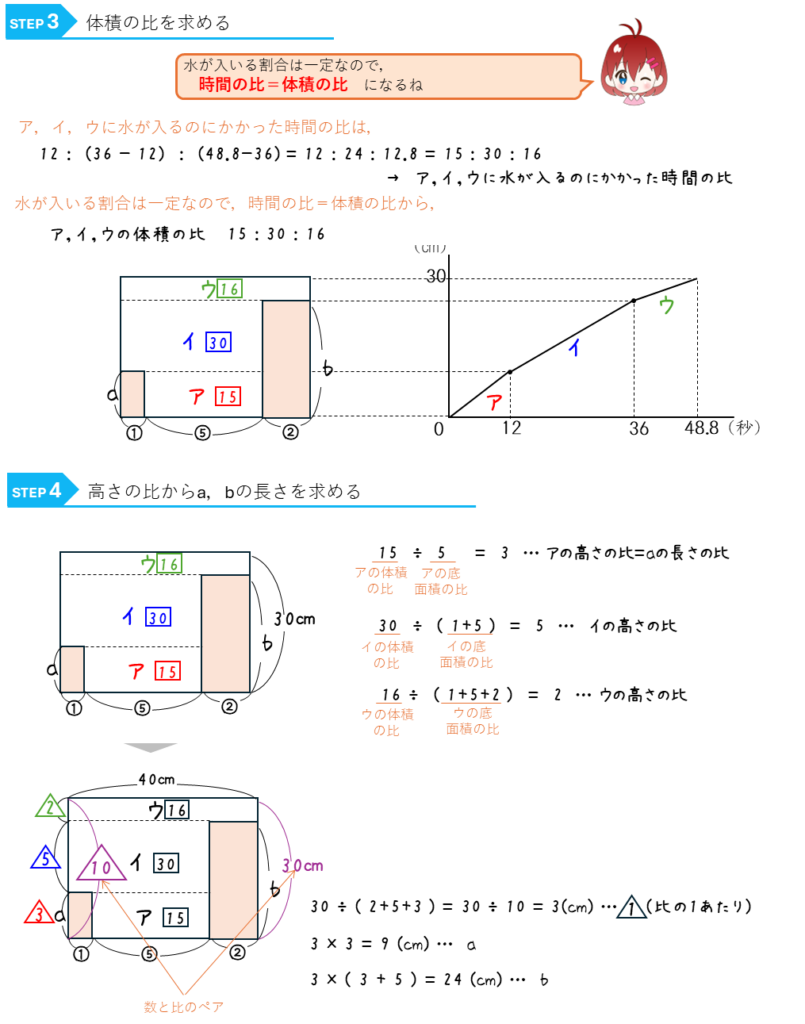
時間の比=容器の体積の比
になり、また、容器の体積については、
容器の体積=容器の底面積×高さ
ですので、高さが一定であれば、
容器の体積の比=容器の底面積の比
底面積が一定であれば、
容器の体積の比=高さの比
となります。さらに、容器が直方体であれば、
容器の底面積=容器の横の長さ×容器の奥行
の奥行が一定になるので、
容器の底面積の比=容器の横の長さの比
という関係があります。それぞれの関係は決して難しいものではありませんが、いろいろな量や比が出てくるところが複雑にしています。正面図をかいて、考えを整理して解いていきましょう。
(四谷大塚 予習シリーズ算数 五年下の解説です。テキストは四谷大塚から購入してください。)
練習問題
水量変化ー物体をしずめる①


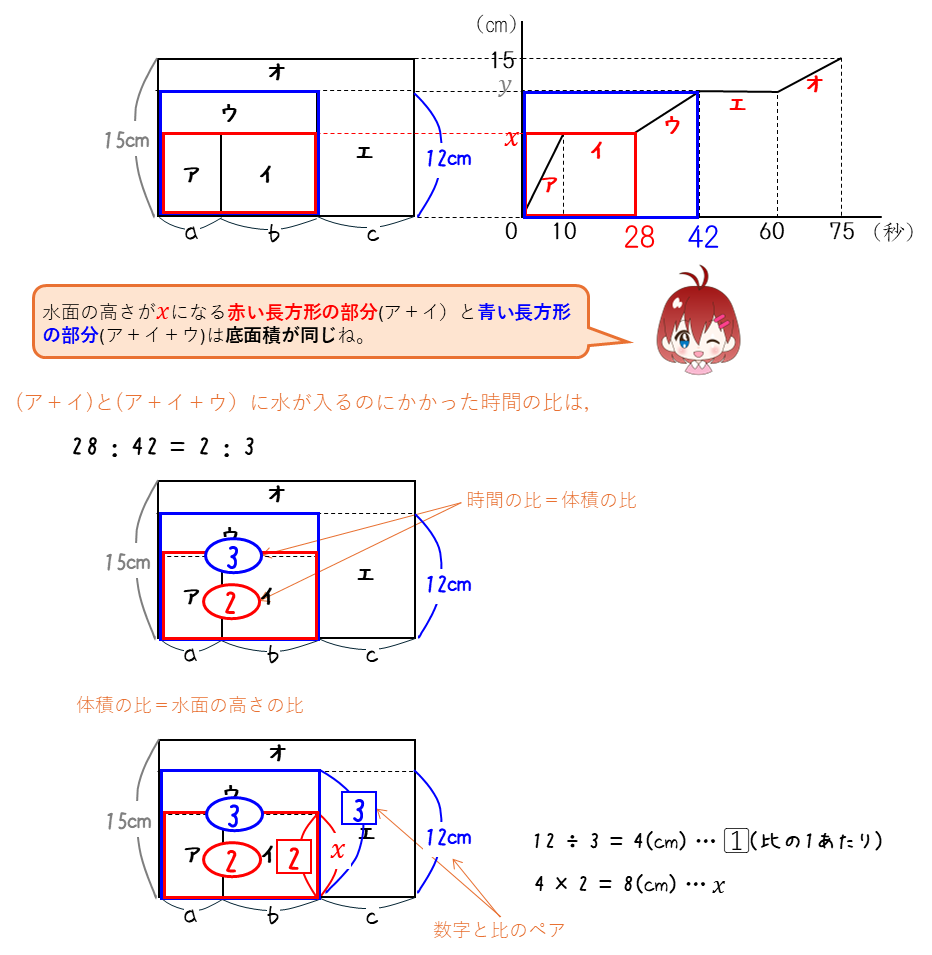
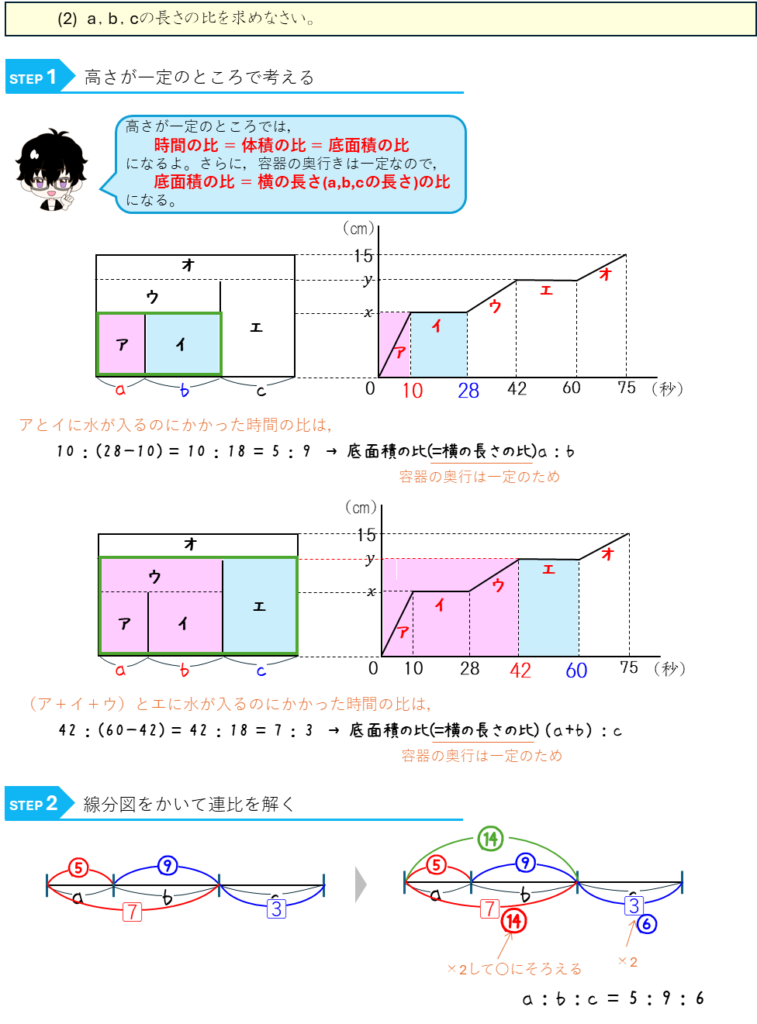
水量変化ー比を使う水量変化のグラフ①


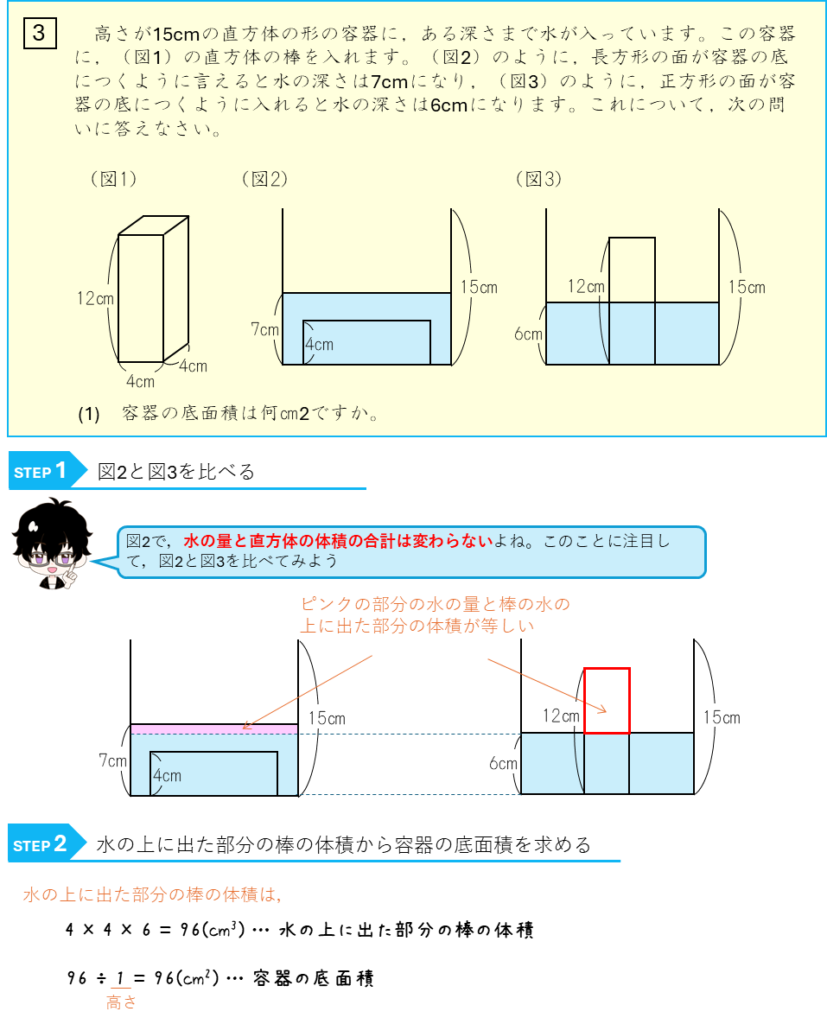
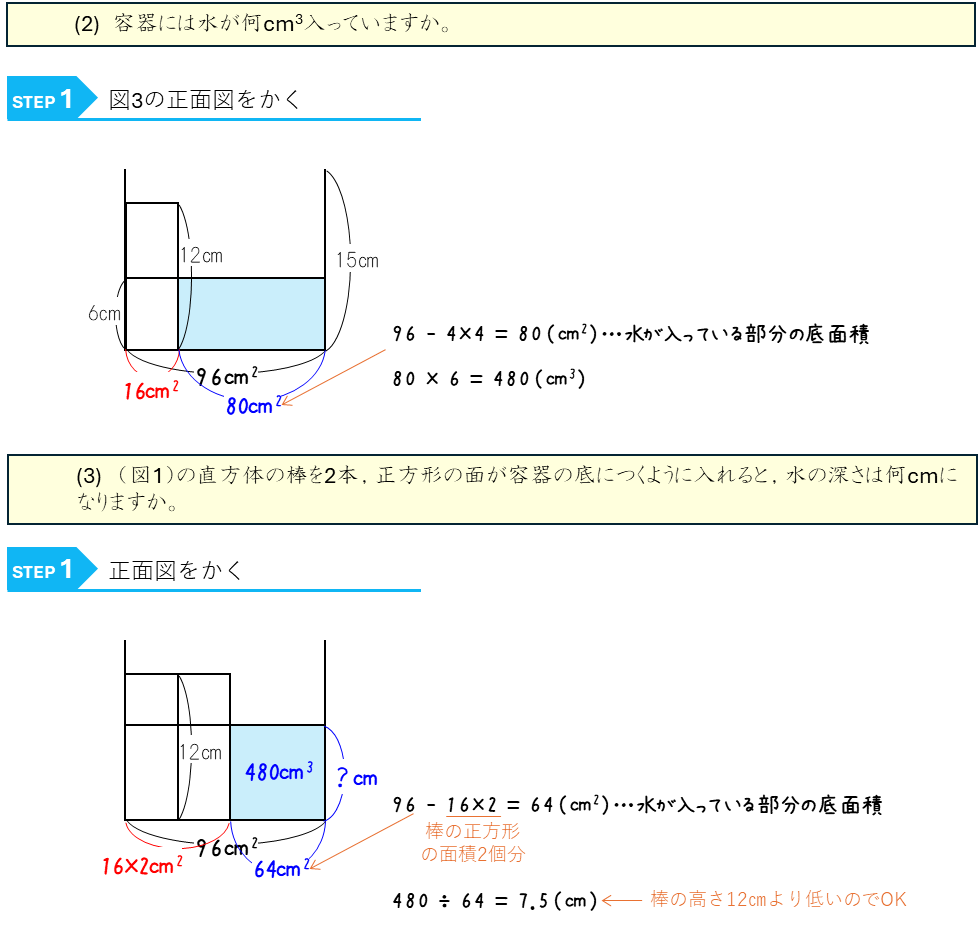
水量変化ー物体をしずめる②
水量変化ー比を使う水量変化のグラフ②

コメント