四谷大塚 予習シリーズ練習問題解説(5年下 第11回仕事に関する問題)

　のべ算は、1人が単位時間にする仕事の比を１として，全体の仕事量(のべ)を考える問題です。

　さらに、今回はニュートン算についても学びます。ニュートン算は，増えていくのと減っていくのが同時におこることを考える問題です。はじめの量、入る量、出る量、時間など量の種類が多く、さらに、複数の場合が出てくるので難易度が高いのですが、線分図や面積図をかいて整理すると、わかりやすくなります。

　かなり分量が多い回なので、まずは基本的な考え方をしっかり理解しましょう。

　（四谷大塚　予習シリーズ算数　五年下の解説です。テキストは四谷大塚から購入してください。)

解説

仕事算

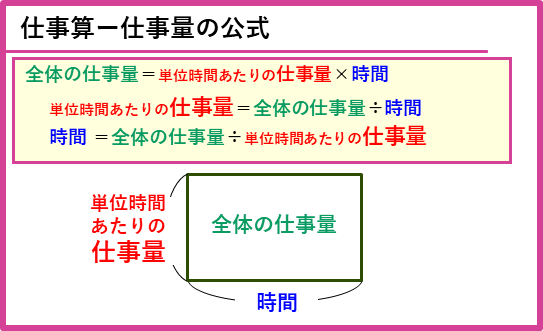
仕事算の公式

　仕事算の3つの公式です。全体の仕事量は、

　　全体の仕事量＝単位時間あたりの仕事量×時間

と、積の式で表されるので面積図をかいて考えることができます。

仕事量を比で表す(逆比で考える)

　仕事算では、仕事をするのにかかる時間だけがわかっていて、具体的な仕事量がわからない問題が多く出題されます。全体の仕事量は一定なので、このような問題では逆比を使って、それぞれの単位時間あたりの仕事量と、全体の仕事量を比で表して解きます。

仕事量を比で表す(面積図で考える)

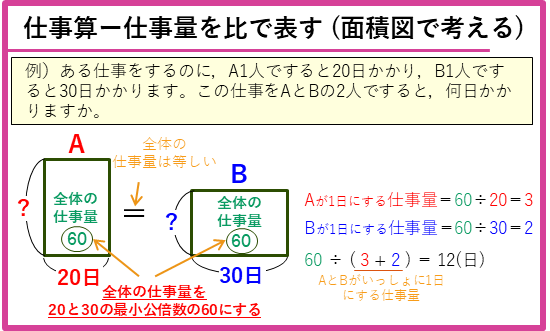
　逆比が苦手という人も多いと思います。そのような人は面積図を使って考えてみましょう。上の逆比を使った問題と同じ問題を考えてみます。

　AとBの仕事量の面積図をかきます。

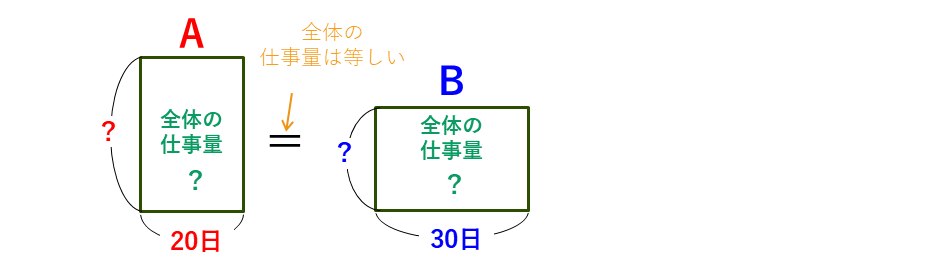
　全体の仕事量も、AとBが１日にする仕事量も分かりません。これらの量を比で表したいので、ここでは、全体仕事量を適当に決めて解き進めていきます。全体の仕事量を、20と30の最小公倍数の60にすると、AとBが1日にする仕事量の比が整数になるので、その後の計算が楽になります。

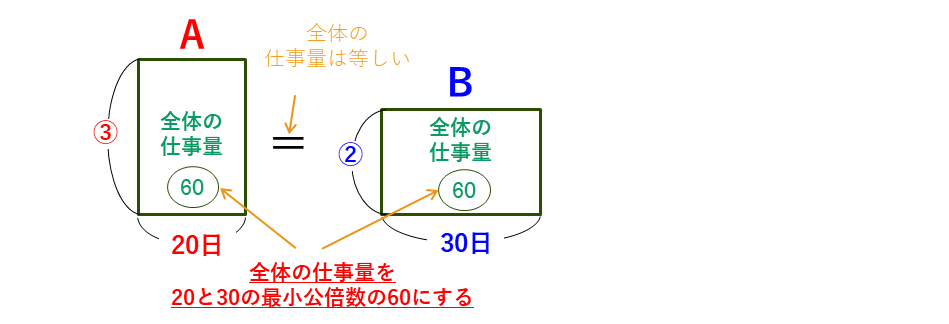
全体の仕事量の比が決まると、

と、AとBがそれぞれ1日にする仕事量の比も求められます。そして、AとBがいっしょに仕事をした場合には、次のようにかかる日数を求めることができます。

　この解き方は、全体の仕事量の比を先に決めたのですが、逆比を使って解いたものと同じになることがわかったと思います。全体の仕事量をかかった時間の最小公倍数に勝手に決めてしまうという点が、はじめはとまどうかもしれません。しかしながら、面積図を使って考えれば、逆比よりも直接的に理解しやすいかと思います。この比を勝手に決めてしまうという考え方は、ニュートン算や相当算でも使うことがあるので、解き方を理解しておきましょう。

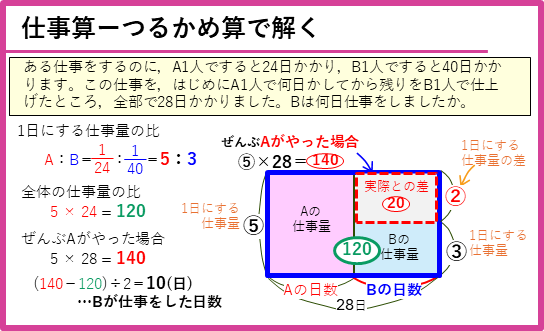
つるかめ算で解く仕事算

　途中で仕事量が変わる仕事算は、つるかめ算で解きます。詳しい解説は、「 面積図で解こう！②－つるかめ算とその仲間たちを分かりやすく解説」の仕事算のところを参照してください。

のべ算

　のべ算は、1人が単位時間にする仕事量の比を１として，全体の仕事量(のべ)を考える問題です。

ニュートン算

ニュートン算は，

　・水がわき出る泉の水をポンプでくみ出す

　・穴があいた水そうに水を入れる

　・毎日はえてくる牧草を牛が食べる

　・行列に次々ならぶ人を入場口から中に入れる

など，増えていくのと減っていくのが同時におこることを考える問題です。

　ニュートン算は、全体の量の線分図をかいて解く方法と、はじめの量が単位時間あたりに減っていく量に注目して面積図をかいて解く方法があります。まずは、基本となる線分図による解法を解説します。

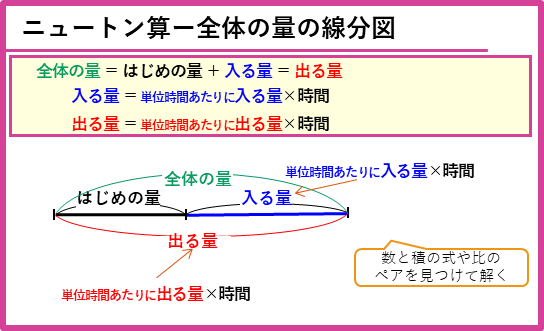
全体量の線分図

　ニュートン算において、泉の水が空になったり、牧草が全部なくなったりすると、水や牧草の全体の量は、次の式のようになります。

　　全体の量 ＝ はじめの量 ＋ 入る量(生える量) ＝ 出る量(食べる量)

これを線部図にかいて問題を解いていきます。

多くの問題では、実際の数と積の式(N×□や□×N)や比(丸数字)とのペアを見つけて解き進めます。次の例題を考えてみましょう。

この例題では、全体の量450Lという実際の数と、くみ出す水の量（□L×30分）という積の式のペアを見つけて、

　　450÷30=15(L)

と、毎分くみ出す水の量を求めます。

複数の場合がある線分図

　ニュートン算では、「ポンプ1台の場合では、、、ポンプ2台の場合では、、、」、「牛が5頭の場合は、、、牛が8頭の場合は、、、」のように、複数の場合がある問題が出題されます。このような問題では、それぞれの場合ごとを線にした線分図をかきます。

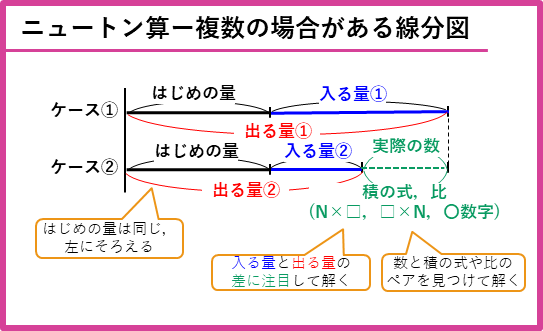
　この線分図のポイントは、

　　・はじめの量は同じなので、左にそろえてかく

　　・2つの場合の入る量と出る量の差に注目する

　　・差の部分で、実際の数と積の式や比のペアを見つける

です。

　ニュートン算の線分図を使った解法の解説については、「線分図で解こう！⑤ー特殊算(ニュートン算・差集め算(過不足算)、ほか)の解き方を分かりやすく解説」も参照してください。

---

ニュートン算の面積図による解法

　ニュートン算は、今まで説明した線分図で解くのが基本ですが、特別な面積図を使って解くこともできます。　まずは、イラストで問題を考えてみます。水そうの問題では、

のように、じゃ口から水が入るのと同時に、排水口から水が出ています。この中身を見てみると実は、

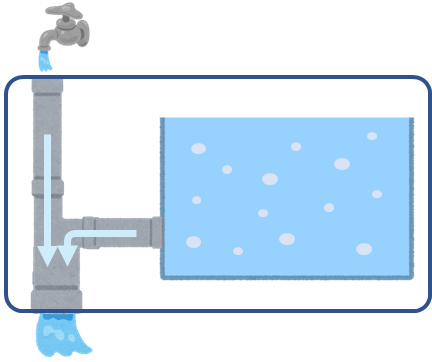
じゃ口の水と水そうからの水が、パイプで合流して排水口から出ていたのです。これをそのまま面積図でかきます。

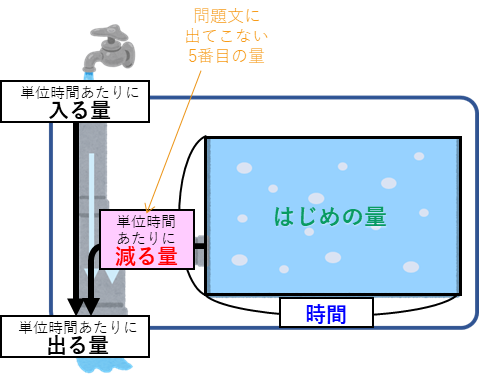
水そうにはじめに入っていた量、空になるまでの時間、じゃ口から単位時間あたりに入る量、排水口から単位時間あたりに出る量、これらは問題に出てきますが、さらに、水そうの水が単位時間あたりに減る量を5番目の量として考えて解いていきます。

　ここで、これらの数には次の関係があります。左の赤い枠は、仕事算や速さと同じで、積の式の面積図になっています。これに、左の枠の、単位時間あたりに入る量、出る量、減る量の関係を加えたものになっています。

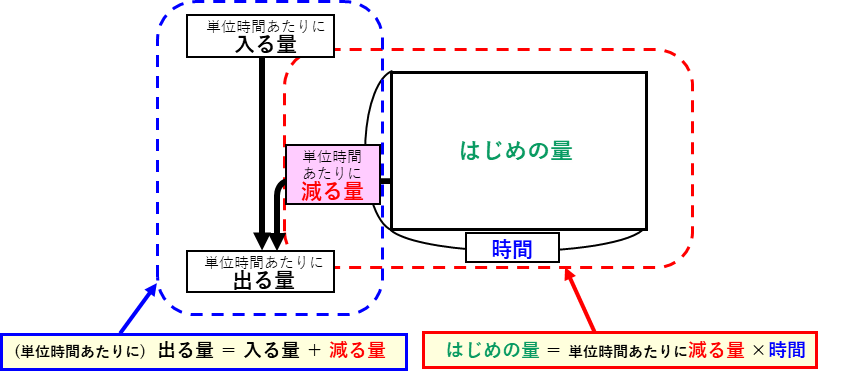
すこし複雑かもしれませんが、このニュートン算の面積図を使うと問題を解くのが楽になります。

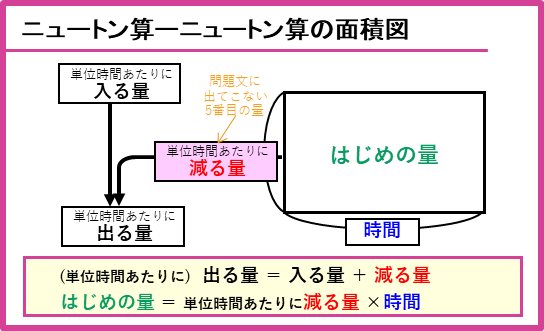
ニュートン算を面積図で解く例

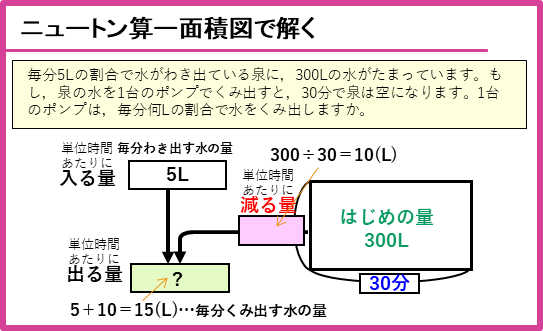
　はじめ量300Lとそれが空になるまでの時間30分が分かっているので、

　　300÷30＝10(L)…単位時間あたり減る量

となります。単位時間あたりのくみ出す量(出る量)は、わき出す量(入る量)と減る量の合計なので、

　　5+10＝15(L)

です。

---

練習問題

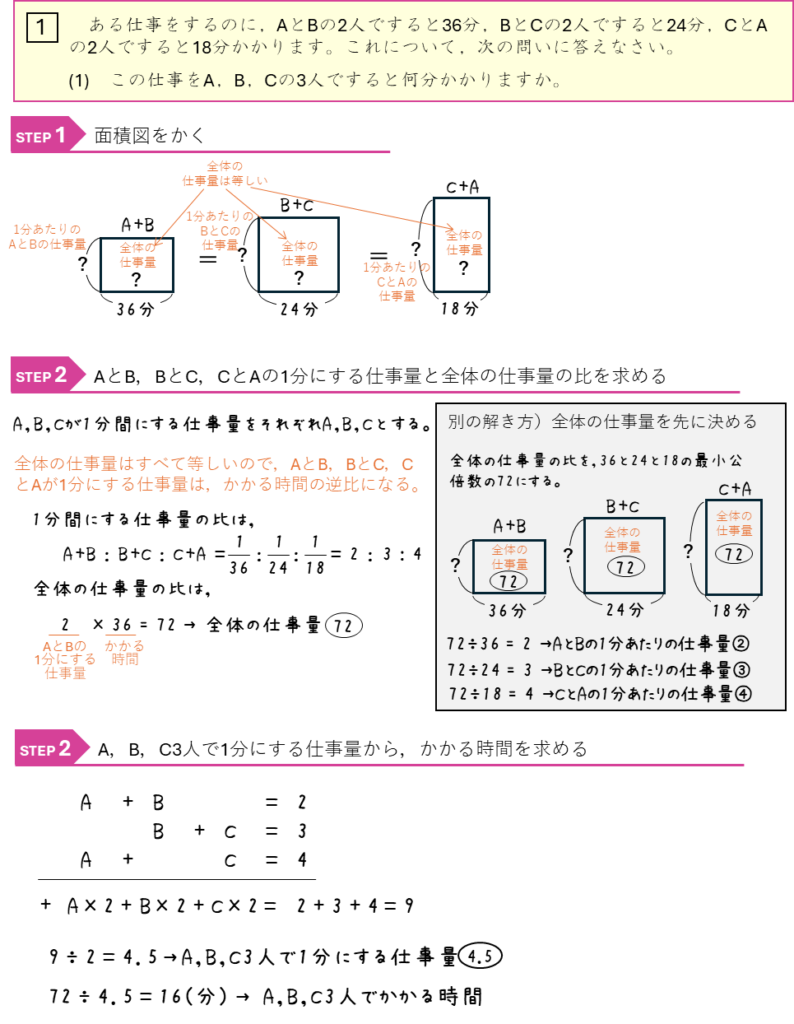
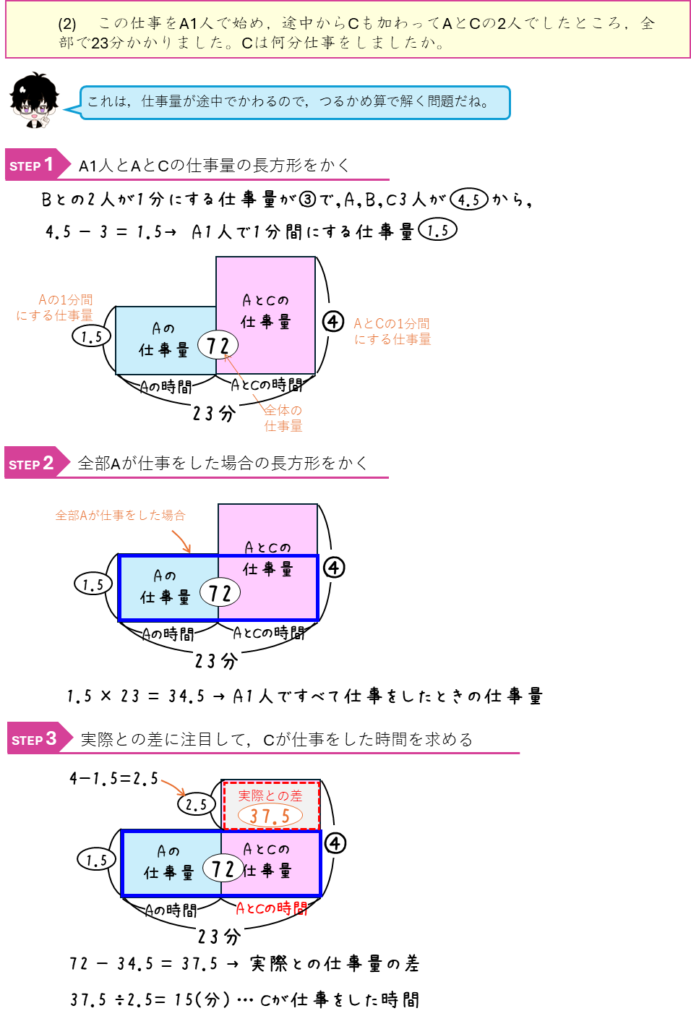
仕事算ー仕事量を比で表す・途中で仕事量が変わる

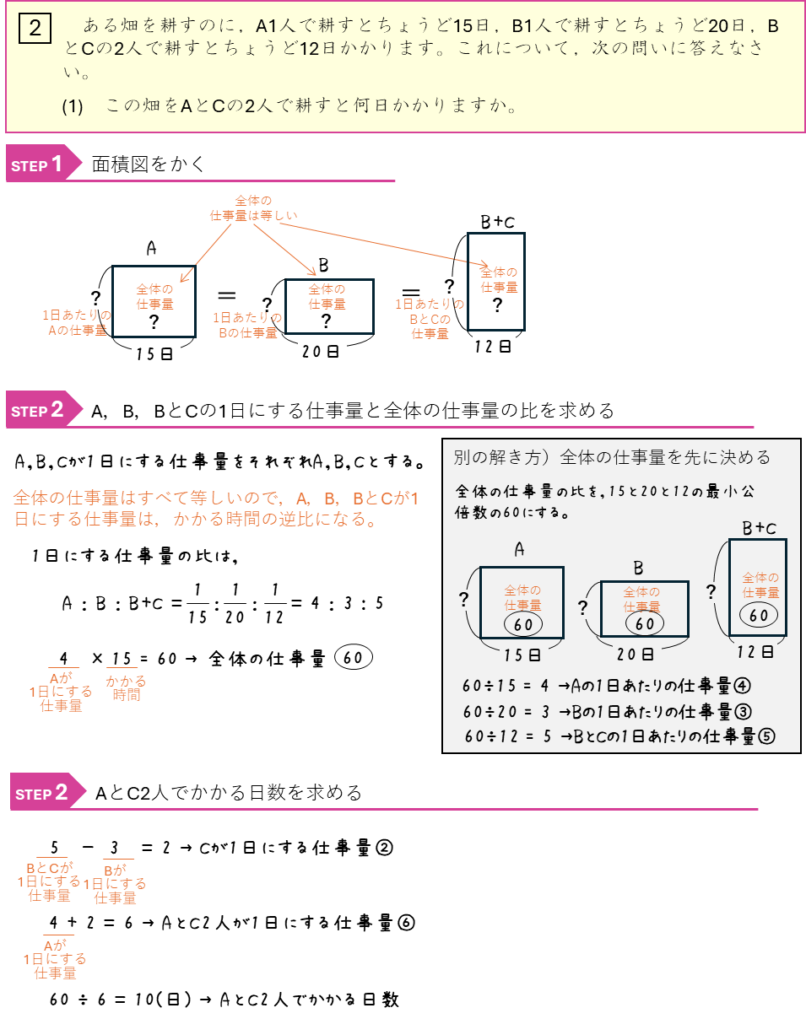
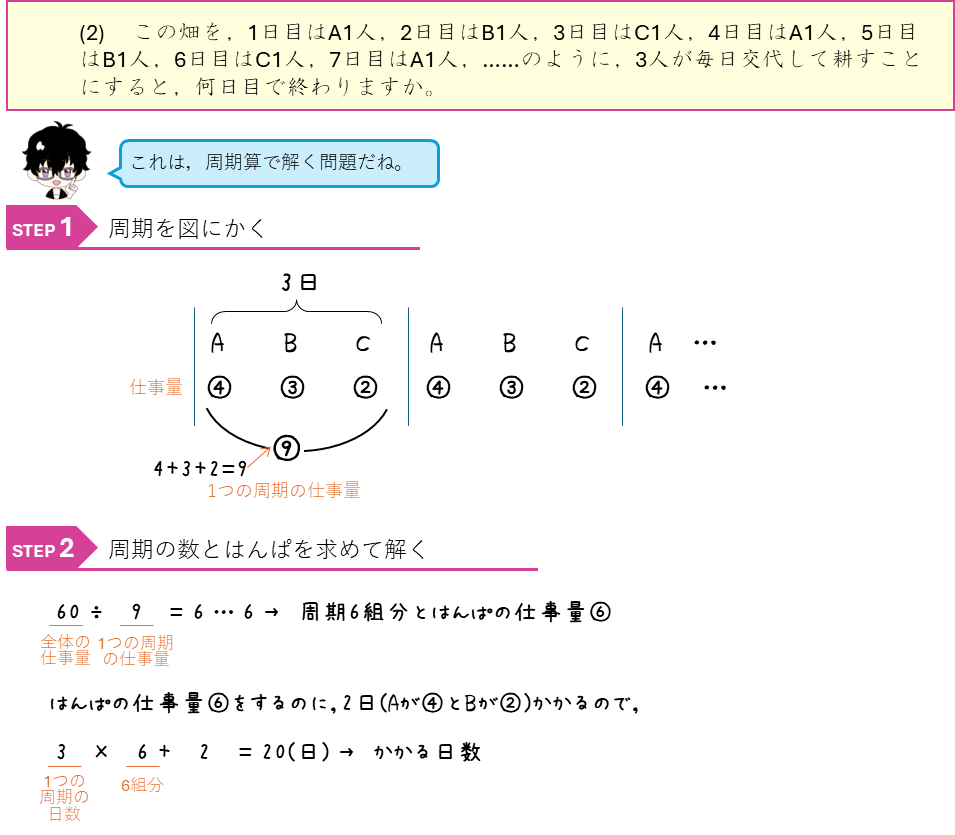
仕事算ー仕事量を比で表す・周期算で解く

のべ算

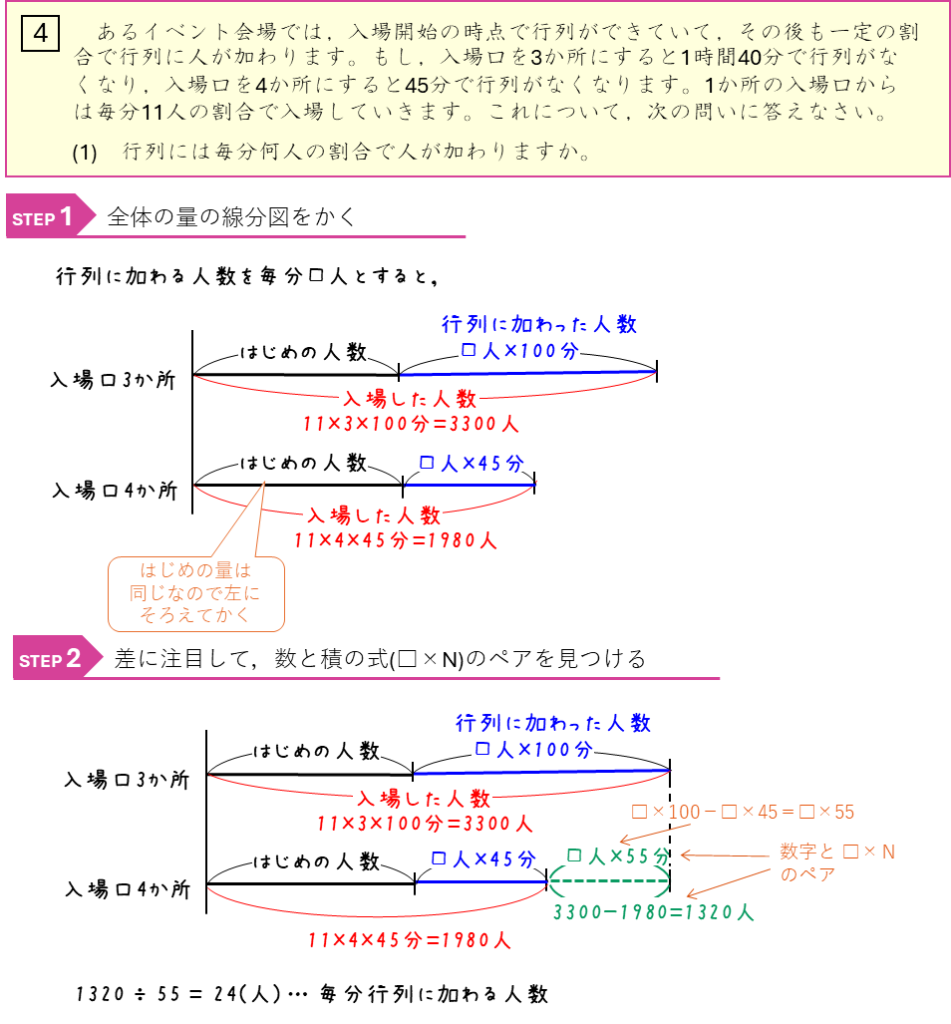
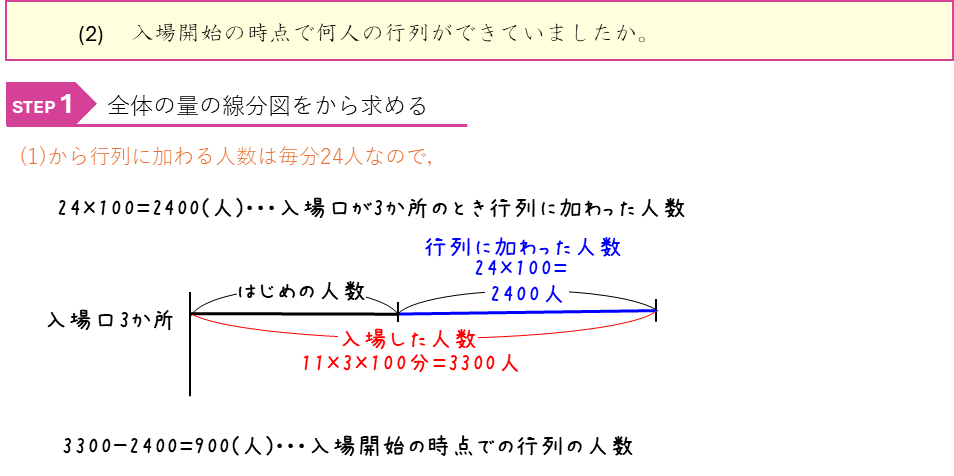
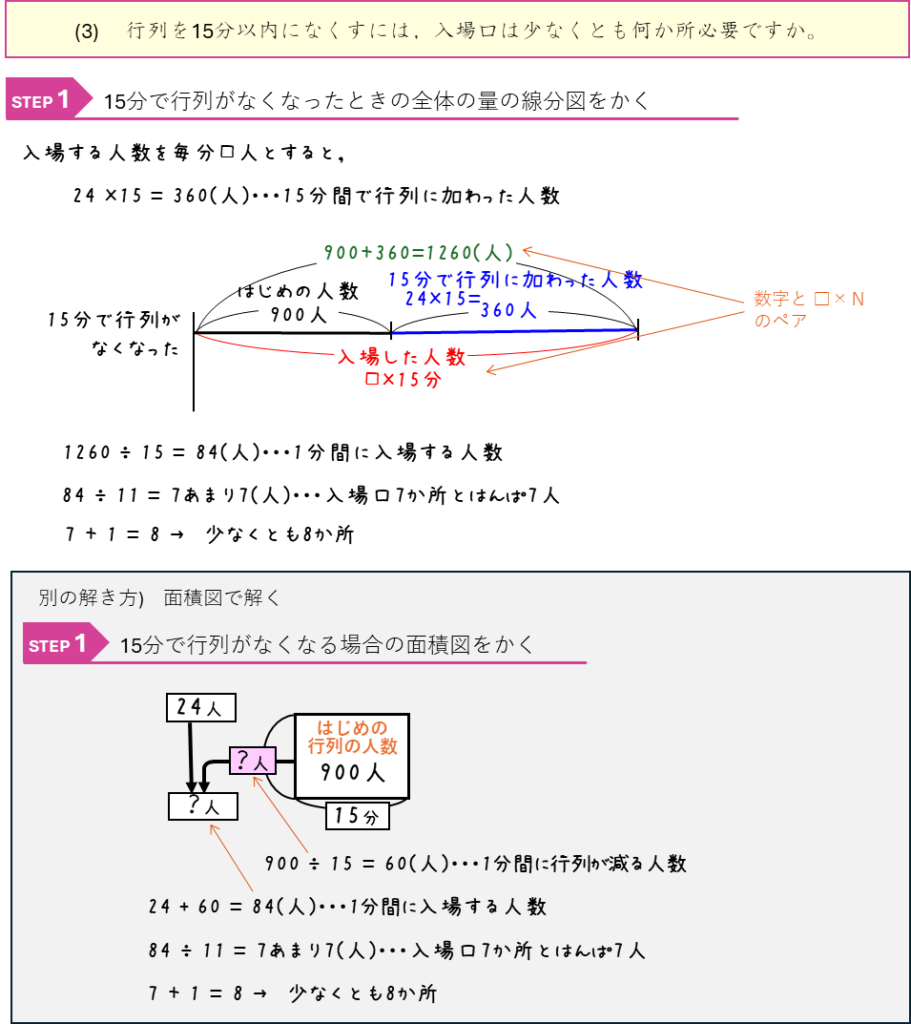
ニュートン算ー行列に並ぶ

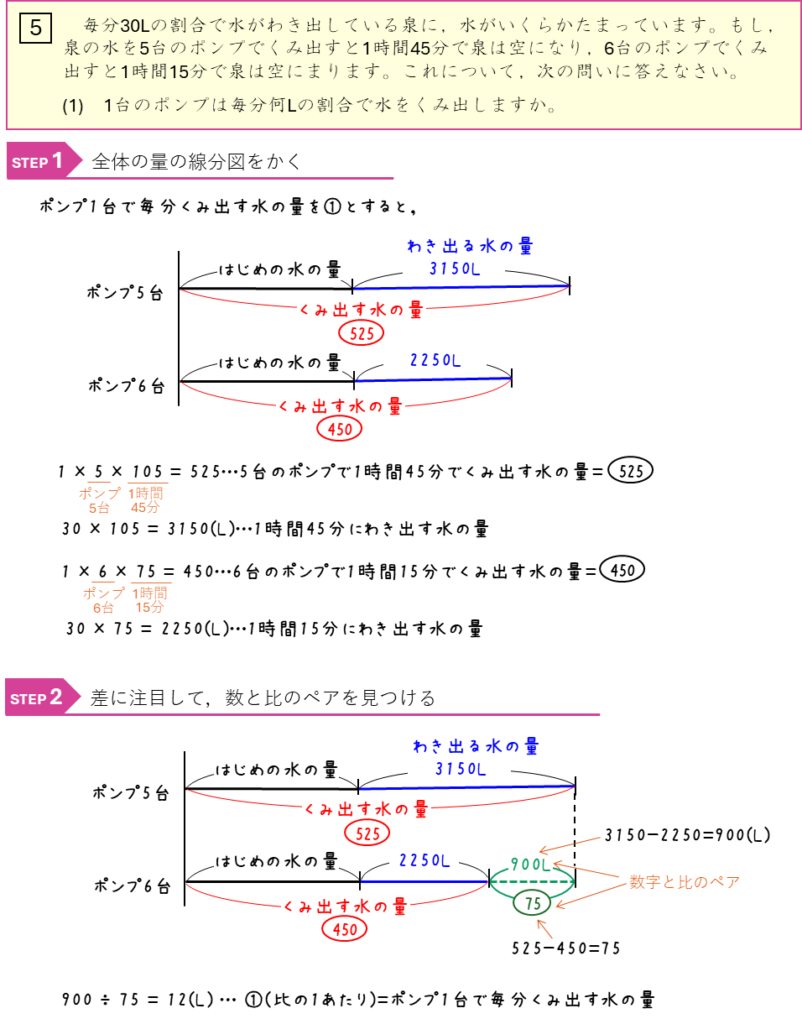
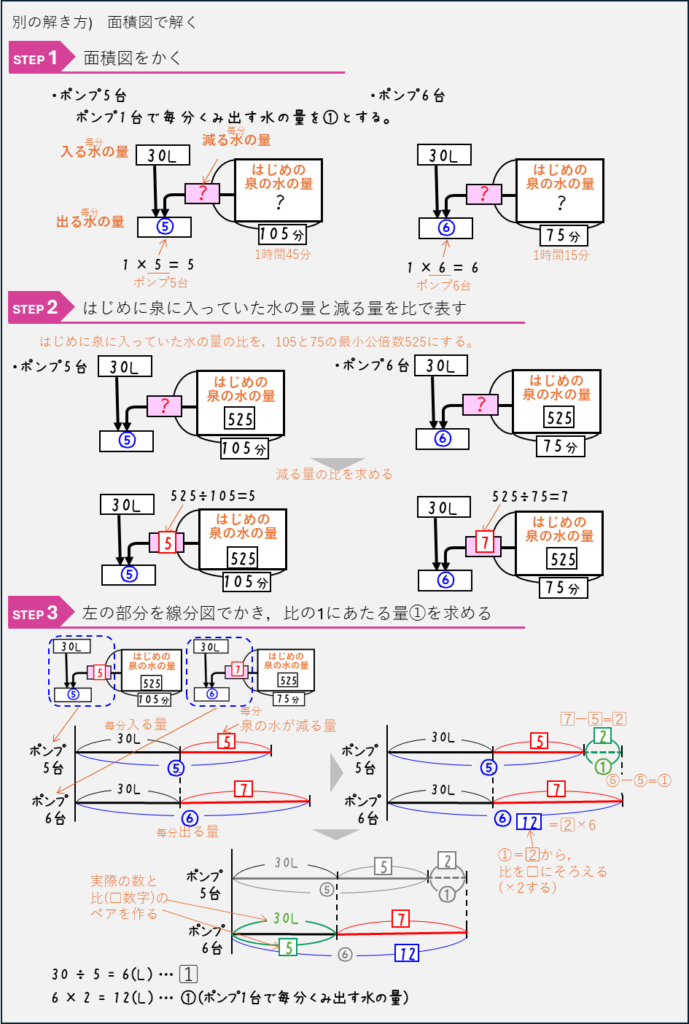
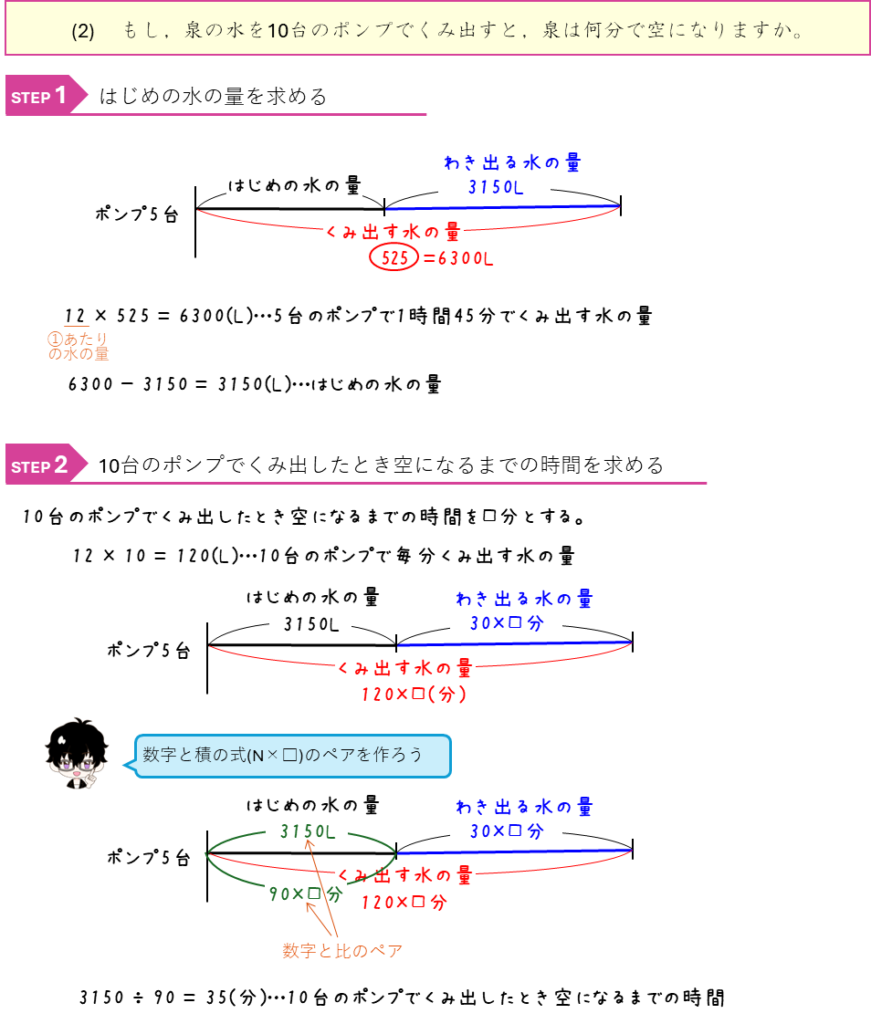
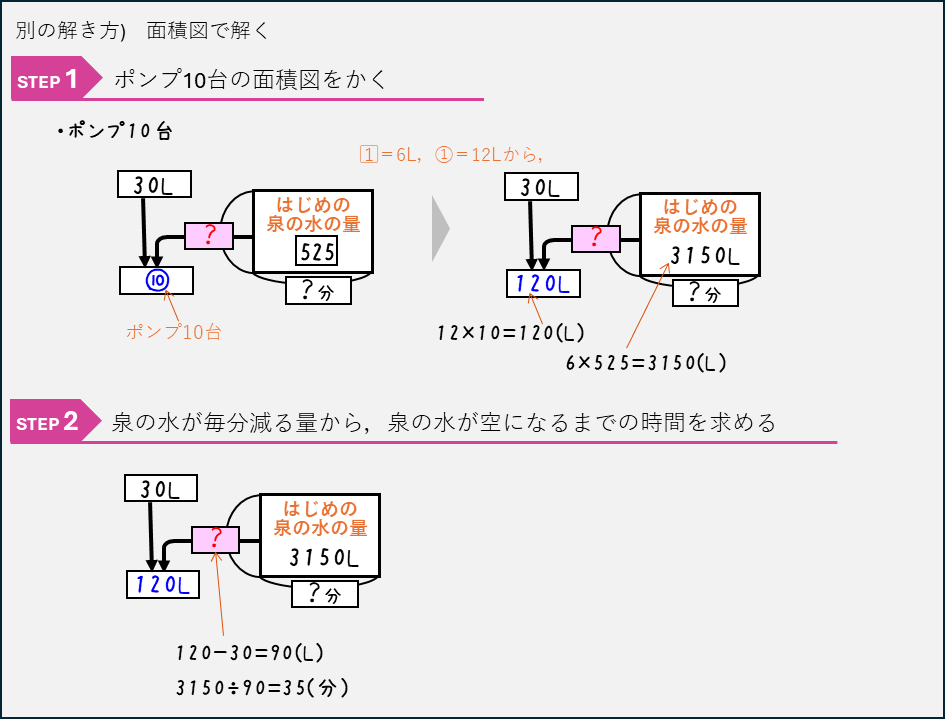
ニュートン算ーポンプで泉の水をくみ出す

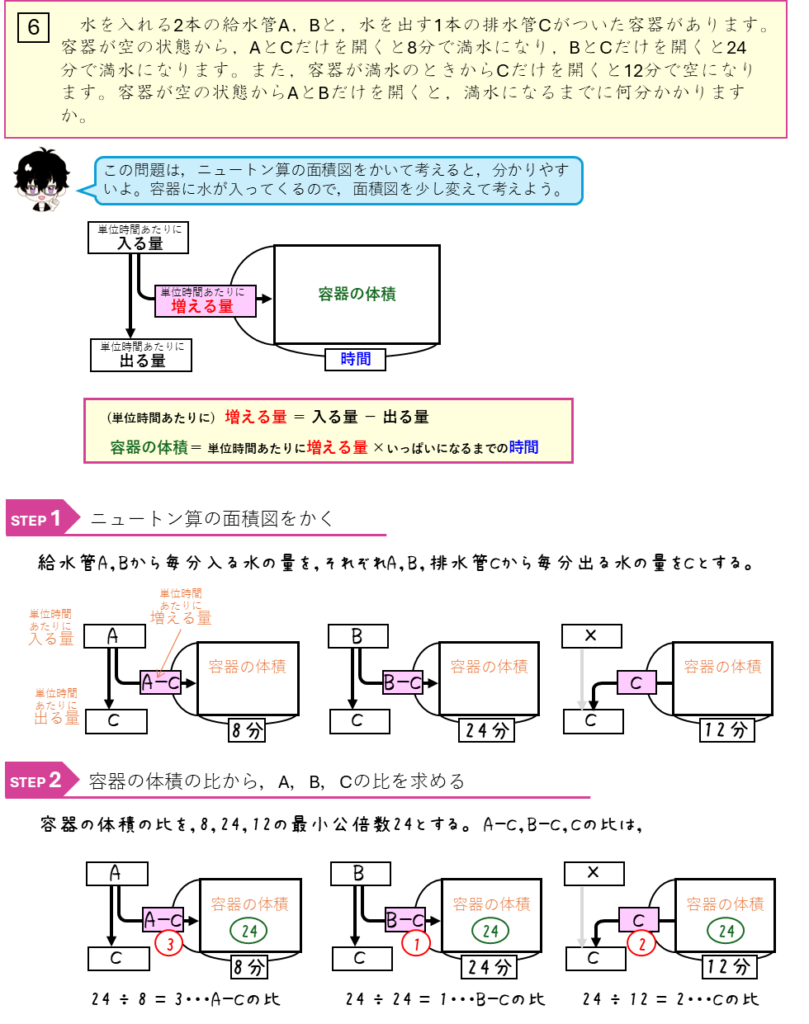
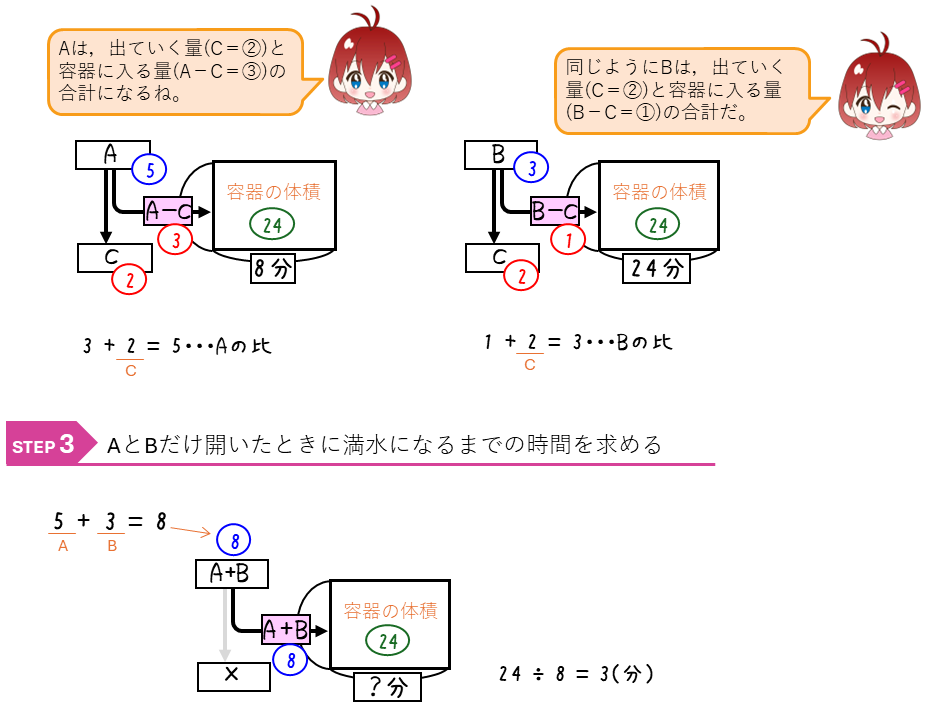
ニュートン算ー容器の体積・増える量を比で表す

---