この単元では、「図形上の点の移動」について勉強します。長さや面積を求める図形の問題、速さの問題、旅人算、速さのグラフなど、今まで学んだ内容を組み合わせる応用問題になっています。それぞれの内容がしっかり身についていないと難しいかもしれませんので、よく理解できているかを確認しながら進めていきましょう。新しい内容としては、単位時間で回転する角度の「角速度」がでてきました。角度の速さですので速さと同じように考えればよいです。円周上の点の移動の問題は、この角速度、旅人算、円の性質、周期が組み合わさった問題なので、難易度が高いものもありますが、1ステップ、1ステップと順に考えを進めて問題を解いていきましょう。(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説

今回は、「図形上の点の移動」について勉強していくよ。点Pが動くので「動く点P」問題と言われたりするけど、長さや面積を求める図形の問題、速さの問題、旅人算、速さのグラフなどが組み合わさった応用問題なのでけっこう難しいかもしれない。それぞれは今まで学んだ内容なので、それぞれの内容がしっかり身についているか確認していこう。
新しい内容としては、単位時間で回転する角度の「角速度」があるよ。角度の速さなので、速さと同じように考えていけばOK。ただ、円周上の点の移動の問題は、この角速度、旅人算、円の性質、さらに、周期が組み合わさった難しい問題もあるので要注意だ。
角速度
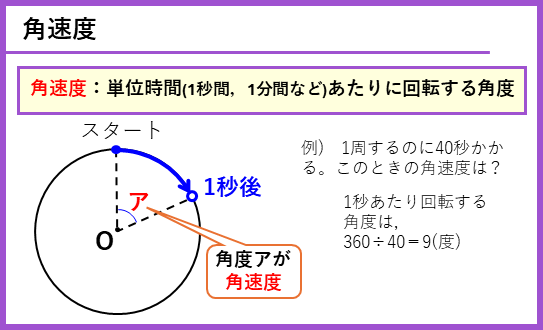
角速度は、1秒間、1分間などの単位時間あたりに回転する角度のことだ。
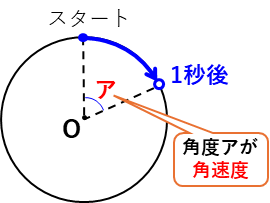


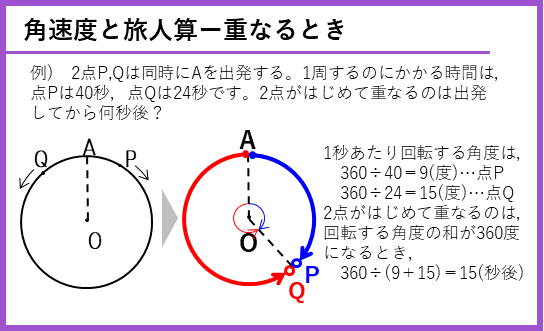
角速度を使うと円周上の旅人算が解けるようになるよ。


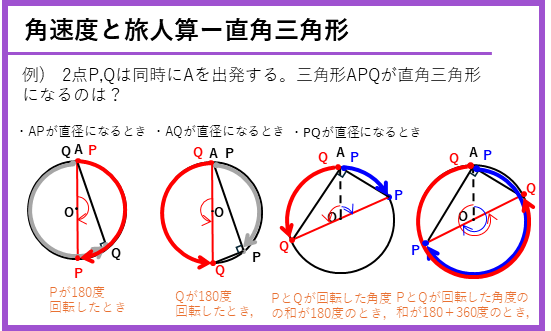
重なるとき以外に、APQの3点が、直角三角形になるとき、正三角形になるときなどの問題にも挑戦していこう。
今回の内容のカードだよ。
練習問題
正方形のまわりの点の移動
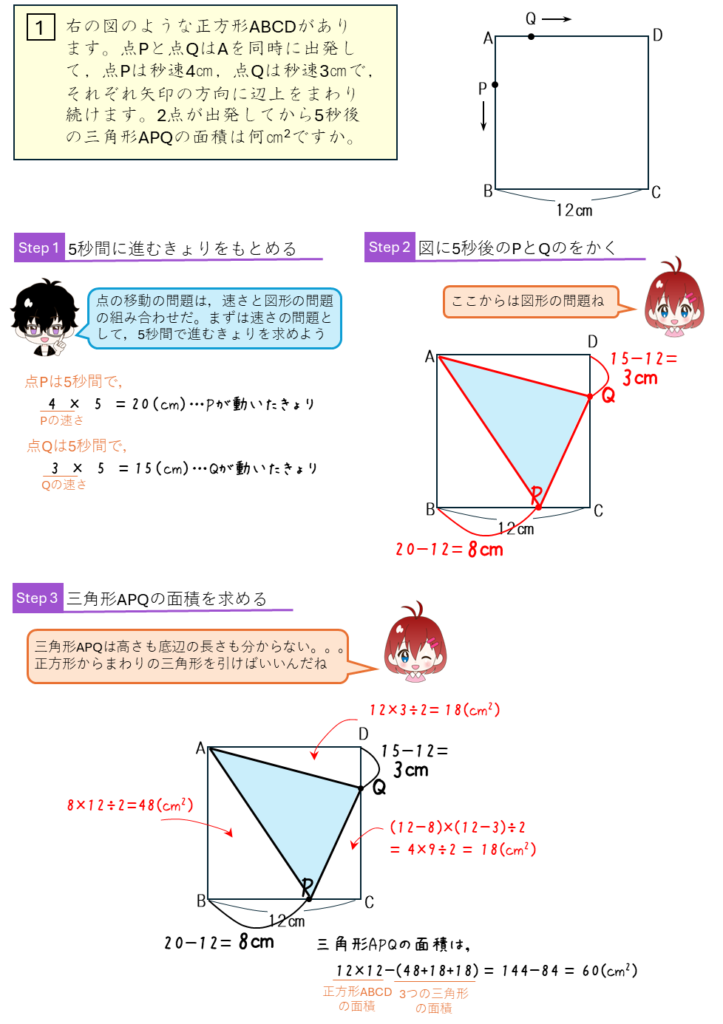
点の移動とグラフ
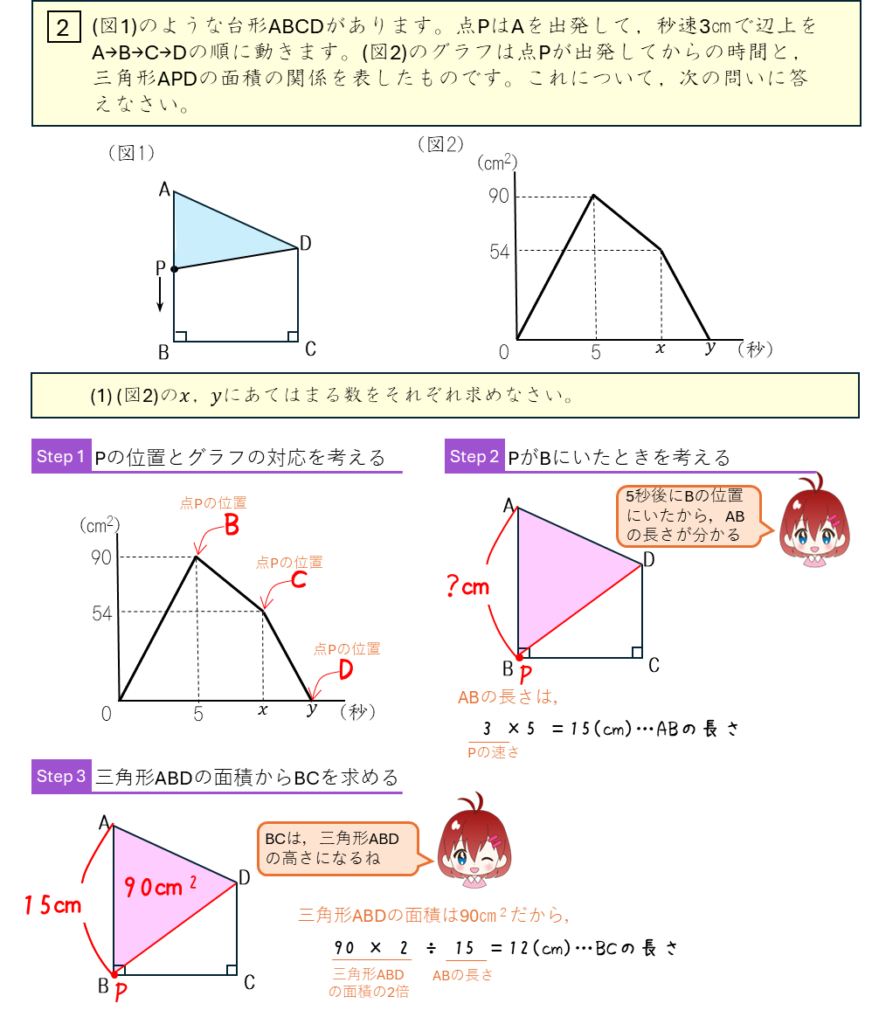
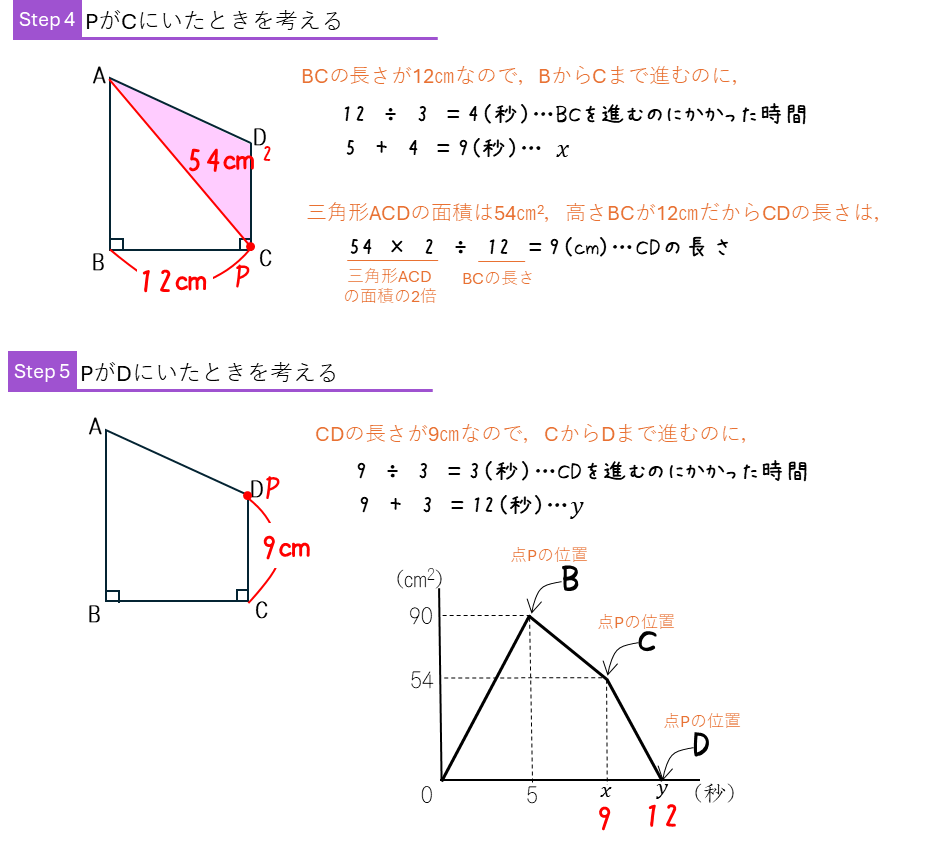
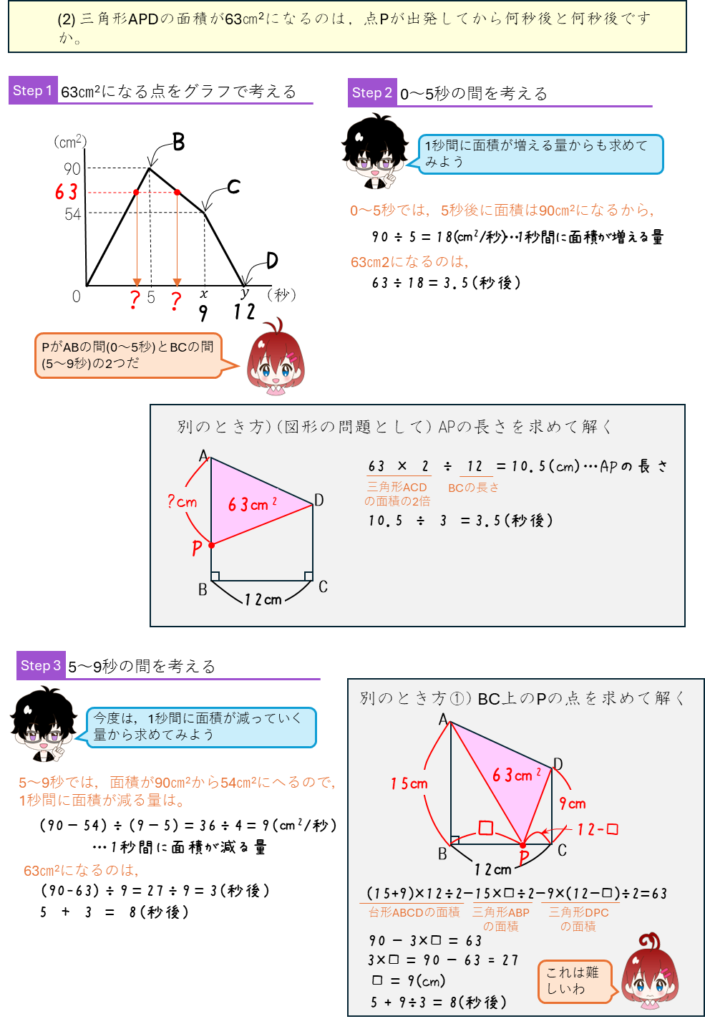

1秒間あたりの面積の変化に注目して解いた方が簡単だったね。速さのグラフの問題は、図形の相似を使うとわかりやすい。相似については5年下期第2回に勉強するので、そのあとに勉強しよう。
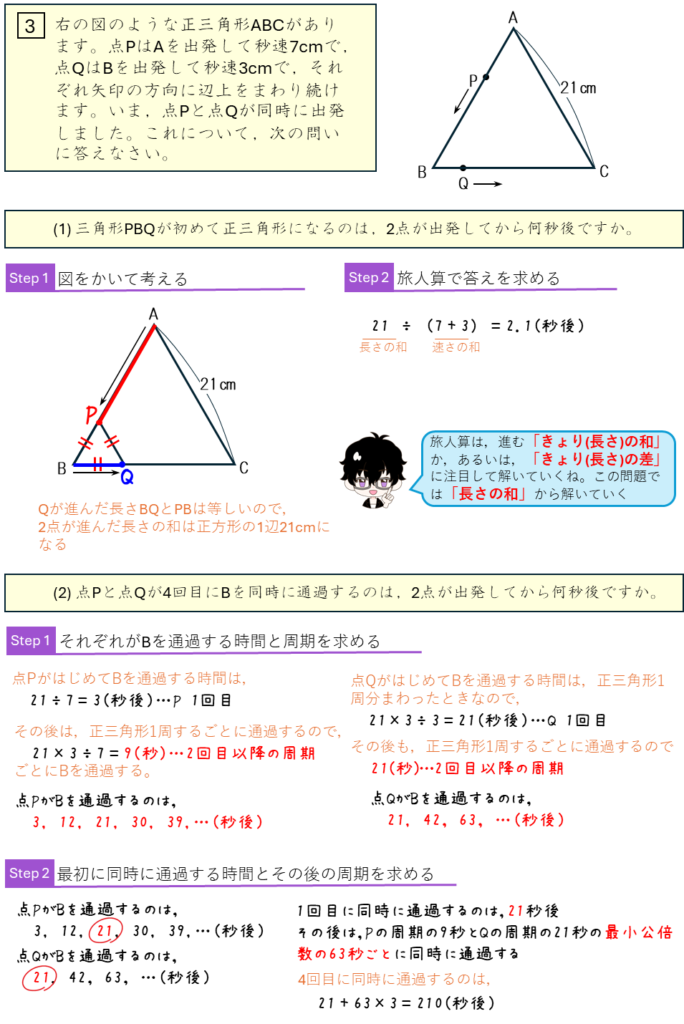
正三角形のまわりの点の移動ー周期
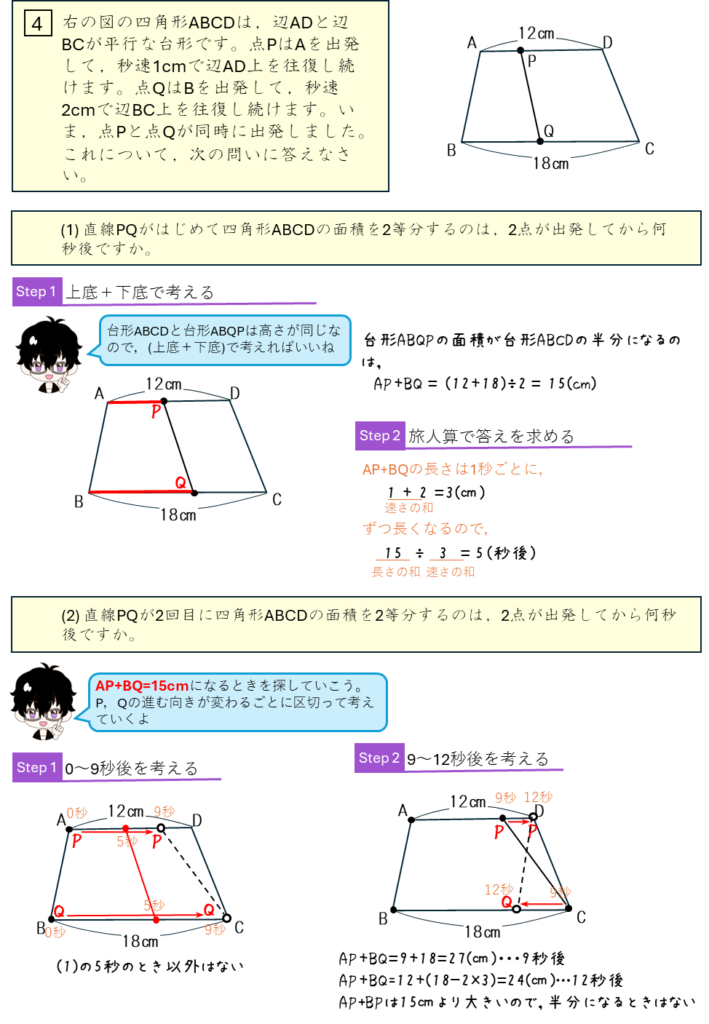
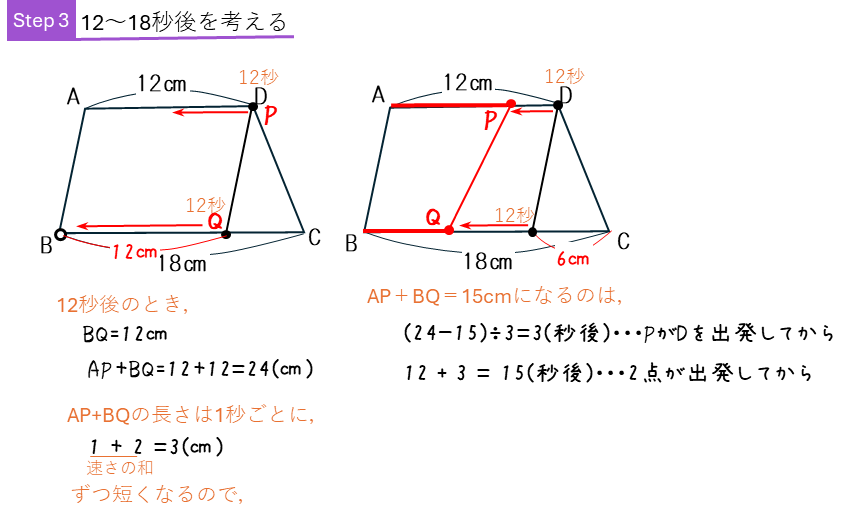
台形の上底と下底の上を点が移動
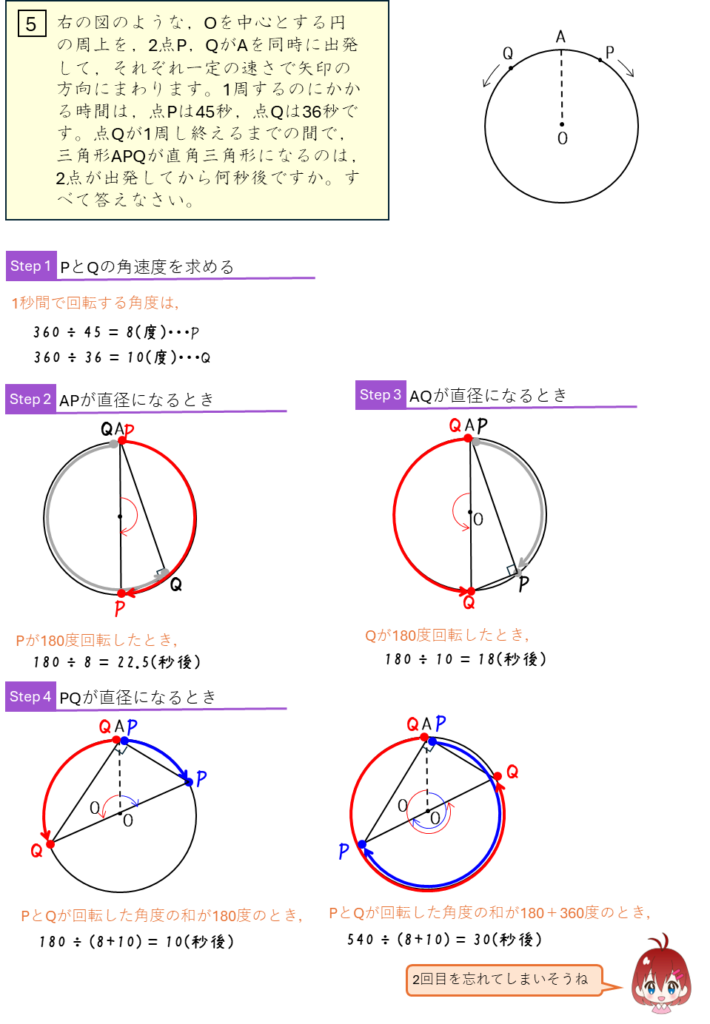
円周上の点の移動

コメント