
前回に続き、「旅人算」を勉強します。池の周りなど円周上をまわる場合や、3人以上の問題をといていきます。旅人算の基本的な考え方は前回勉強した通りで、2人が反対の方向に進む場合は2人の速さの和で近づいて、2人が同じ方向の場合は2人の速さの差で追いかけることになります。その応用としていろいろな問題にチャレンジしいきましょう。グラフの問題では、2人のきょりの変化を表したグラフの問題をときます。グラフの意味を理解することが大切です。2人のきょりのグラフのままでは難しいので、通常の「時間ときょりのグラフ」に図をかきかえることも勉強します。
(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説
今回は、前回に引き続き「旅人算」について勉強していきます。池の周りをぐるぐる回る場合や3人の旅人の問題など、応用問題に挑戦していきましょう。旅人算の基本的な考えは、前回勉強した通りです。「2人の近づく速さ」は、2人が反対の方向に進む場合は2人の速さの和、2人が同じ方向の場合は2人の速さの差になるので、新しい問題でもこの速さと、「2人のきょり」に注目していこう。
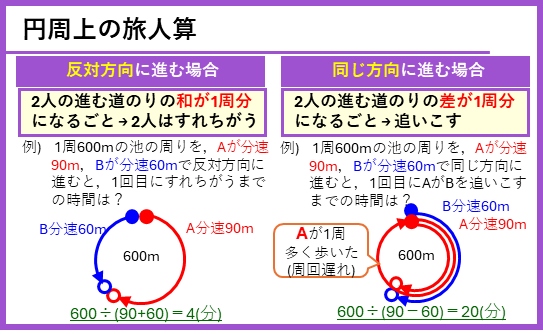
今回、新たに勉強する円周上をまわる問題では、「2人のきょり」は、
・反対方向に進む場合
2人の進む道のりの和が円周の1周分になるごとに、2人はすれちがう
・同じ方向に進む場合
2人の進む道のりの差が円周の1周分になるごとに、追いこす
ことになります。図で確認しておきましょう。同じ方向については、リレーでの周回遅れ(1周分遅れて抜かされる)をイメージするといいです。
「2人の近づく速さ」は、反対方向では2人の速さの和、同じ方向では2人の速さの差になるのは、他の問題と同じです。
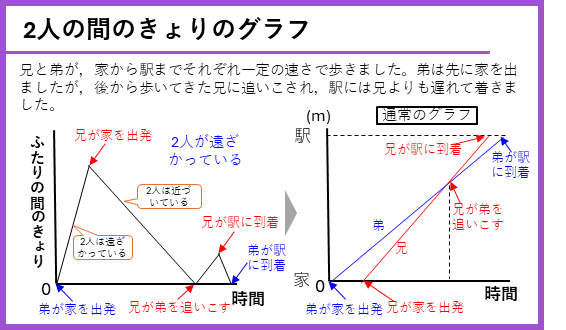
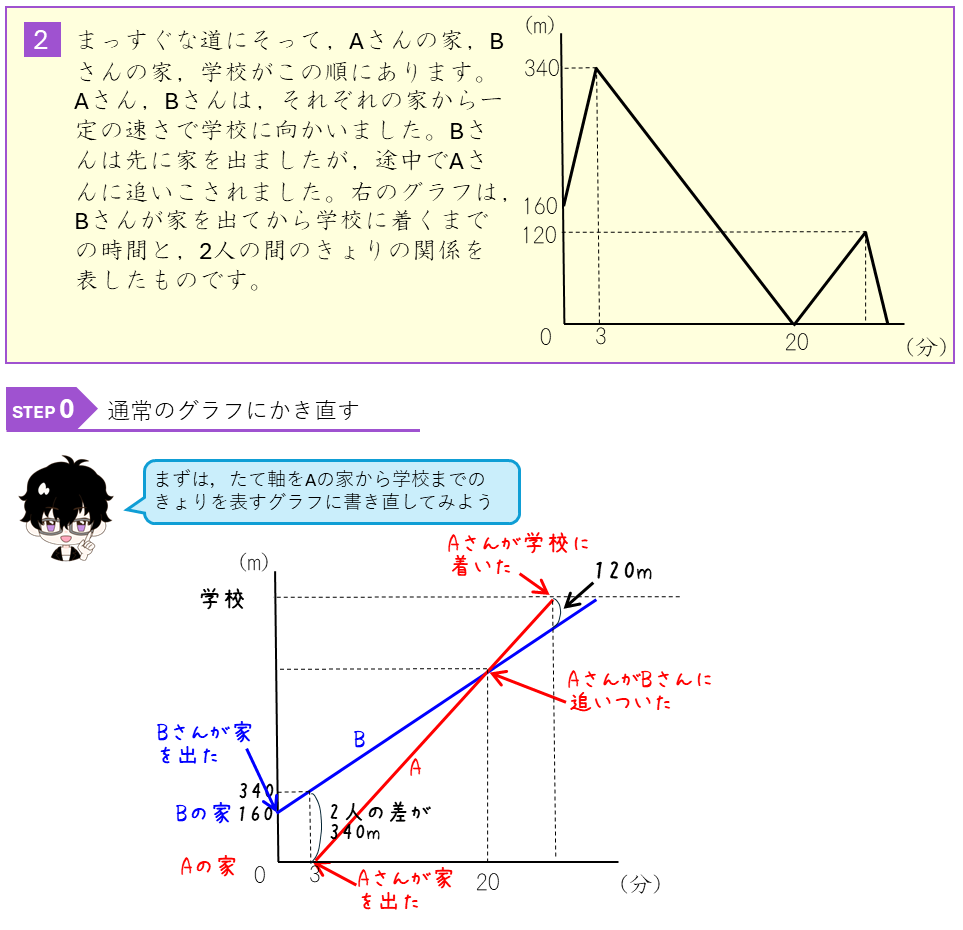
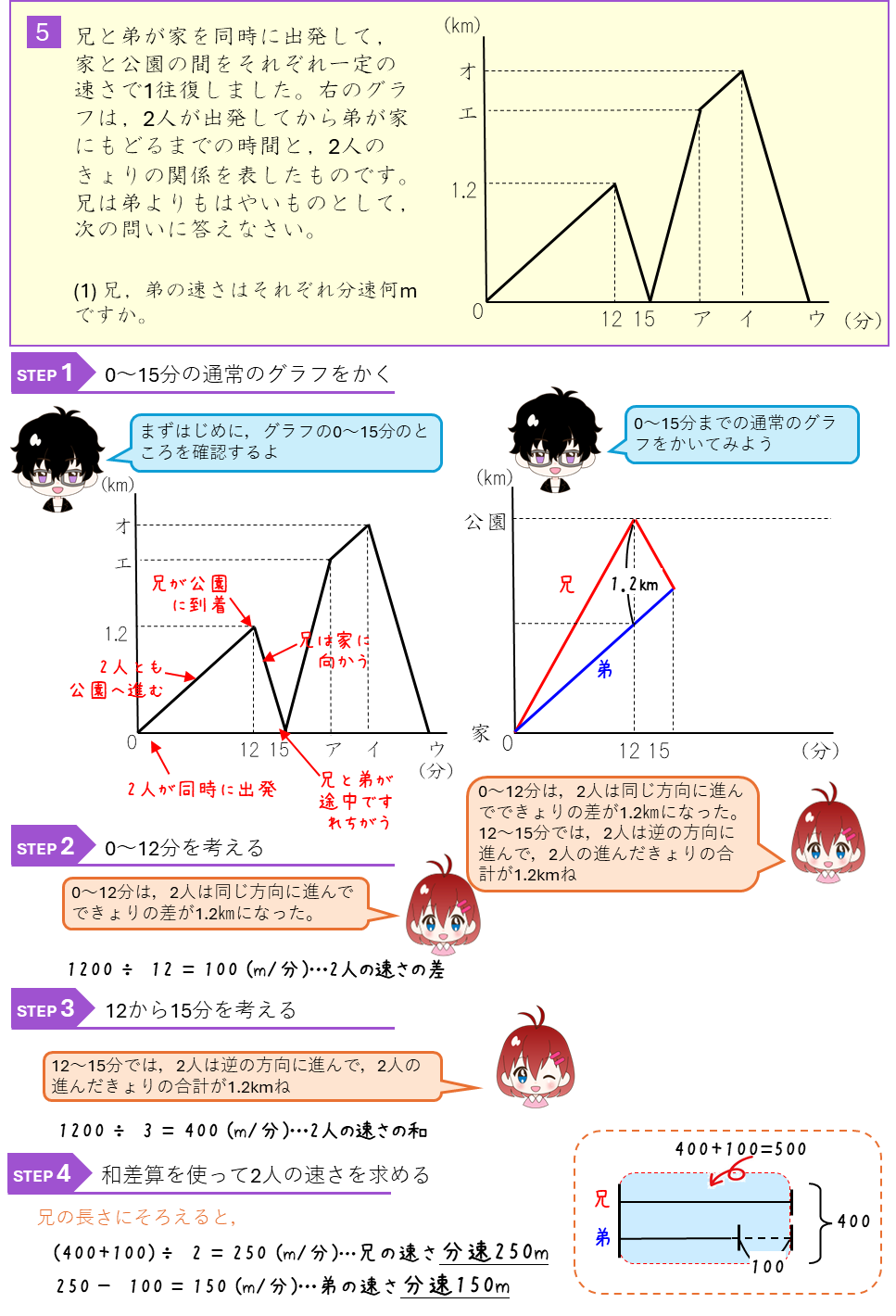
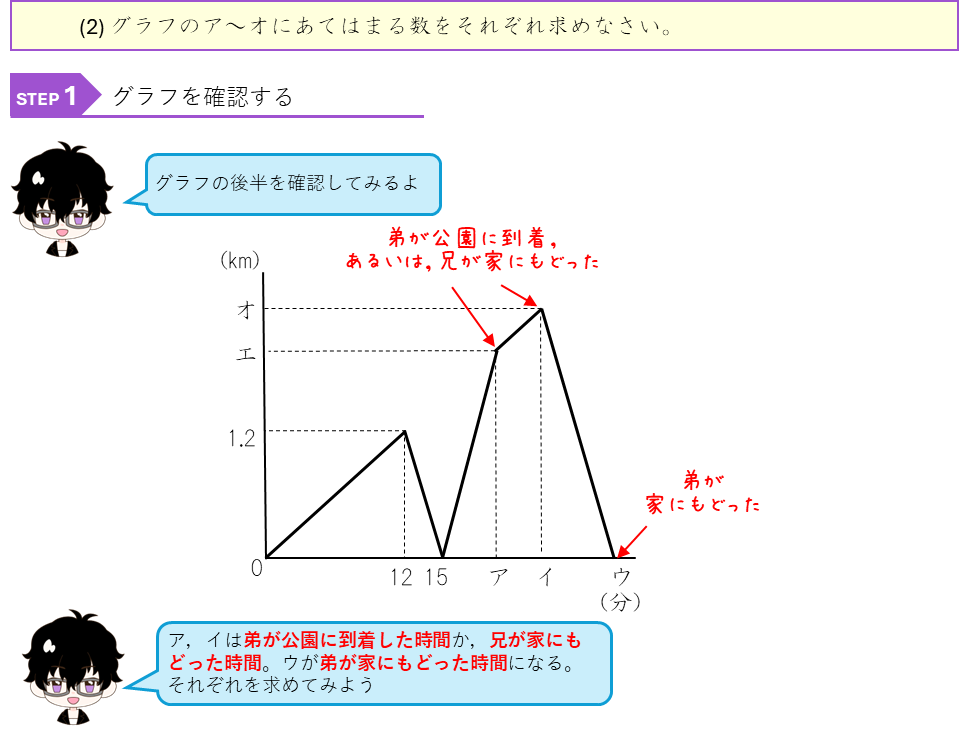
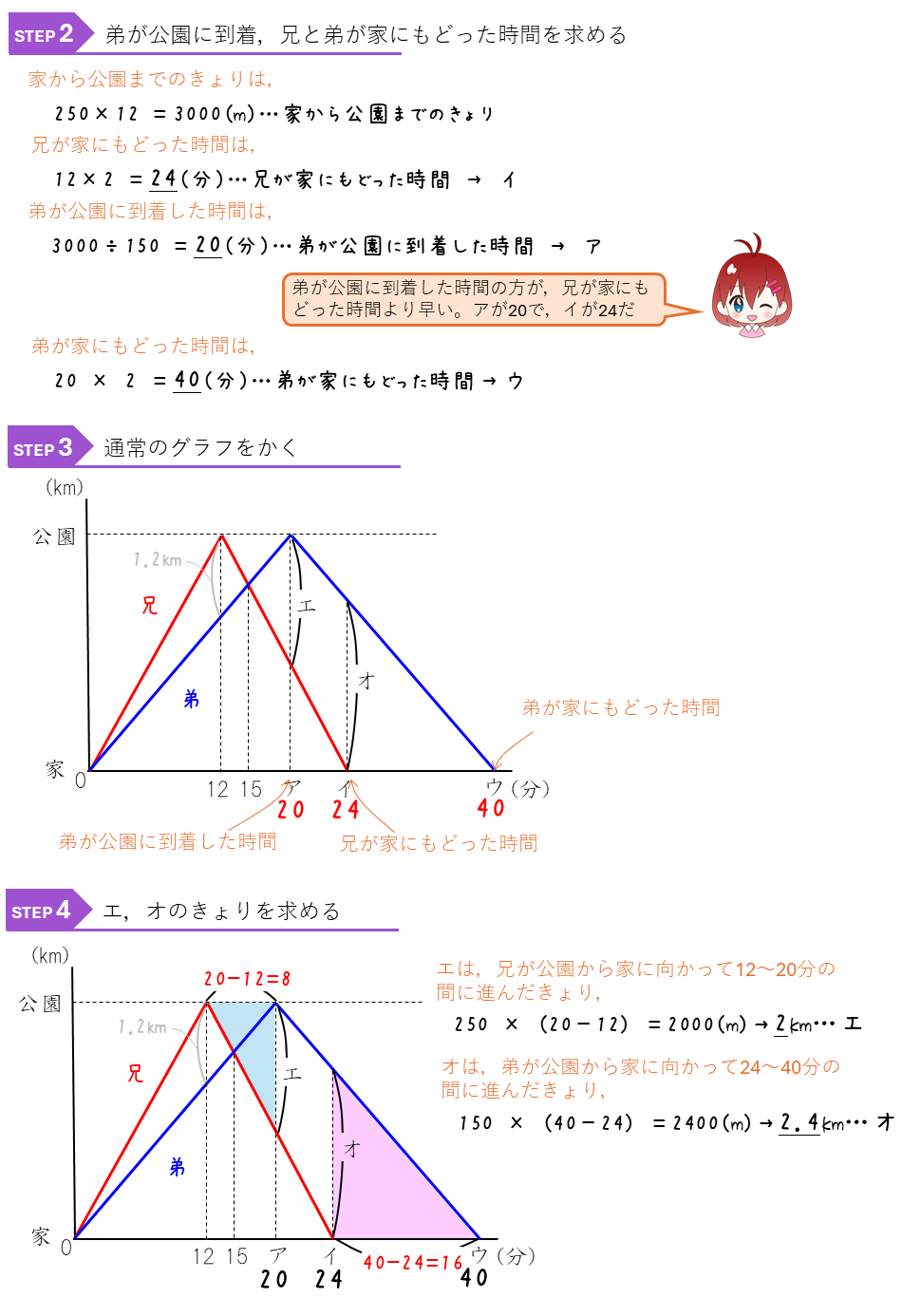
前回、旅人算のグラフの問題をときました。普通のグラフでは、横が時間で、たてが家や駅、公園といった場所のきょりを表していました。今回は、たてが2人の旅人の間のきょりを示したグラフの問題をといていく。このグラフで、
・線が右に上がる場合は、2人のきょりが増えているので、2人は遠ざかっている
・線が右に下がる場合は、2人のきょりが減っているので、2人は近づいている
ことを表しています。あと、ふたりのきょりが0になるところは、すれちがったり、おいこしたりしたところになります。
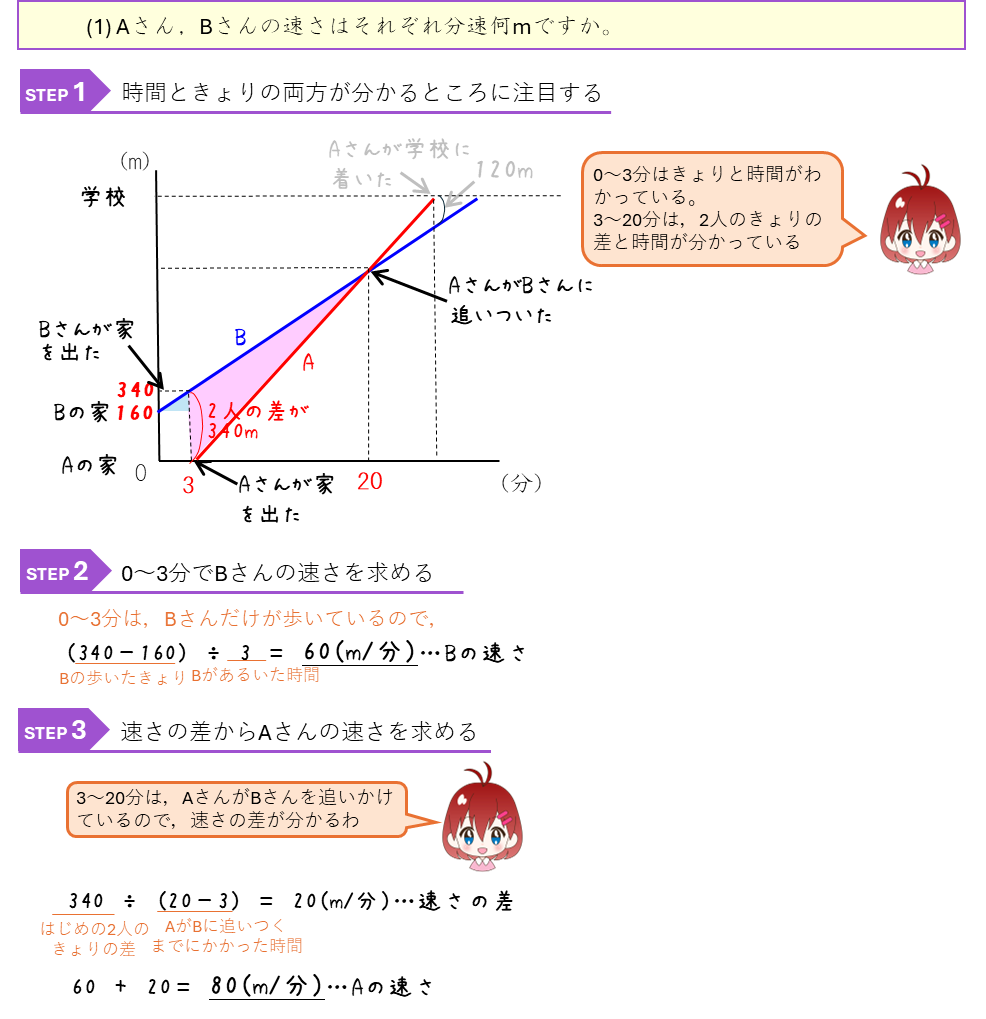
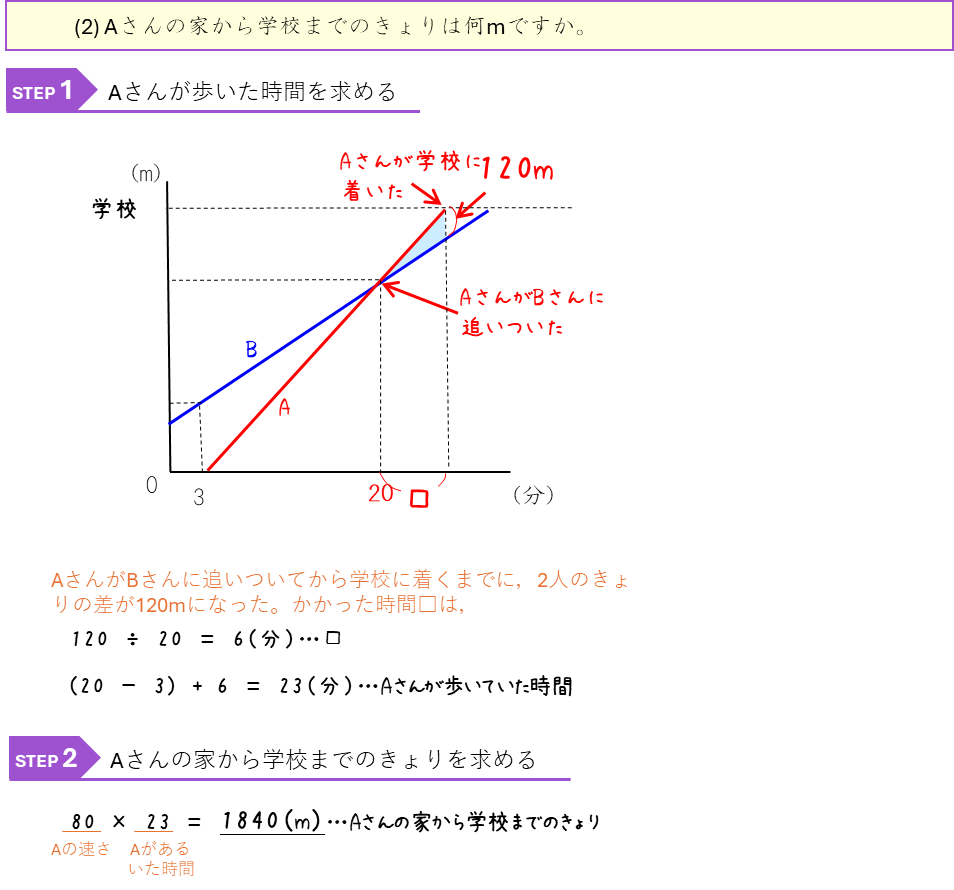
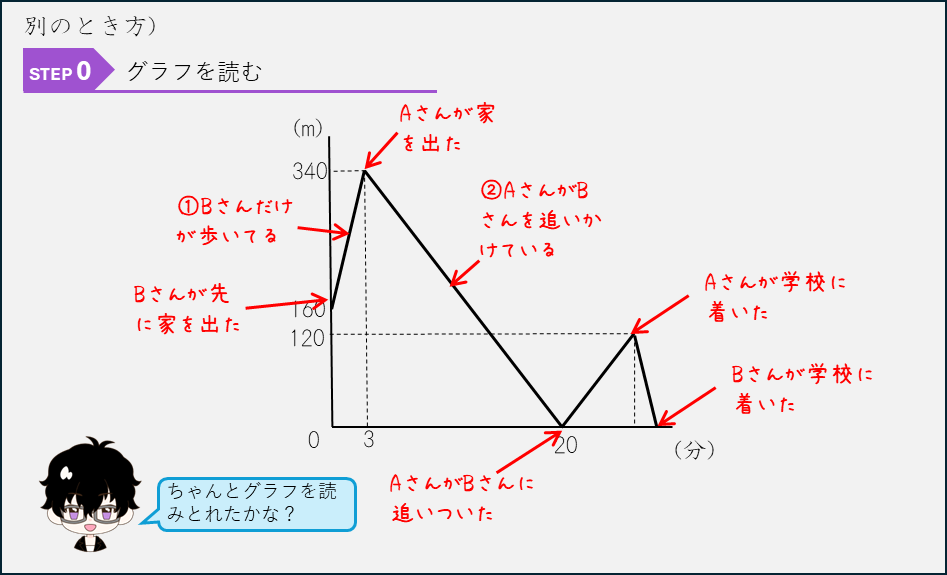
2人のきょりのグラフが何を表しているか理解できるようにしましょう。また、2人の間のきょりのグラフを、通常のグラフ(たてが家や駅などのきょり)にかきかえて問題をといていくことも勉強しておこう。
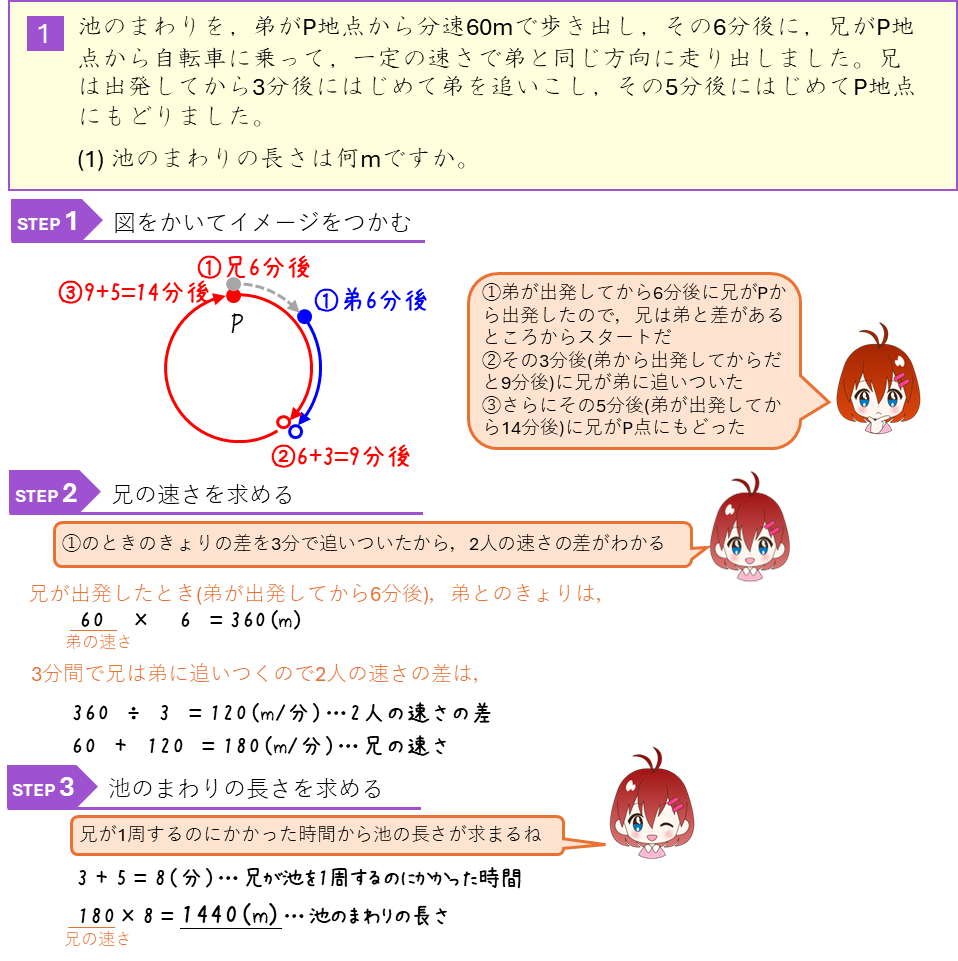
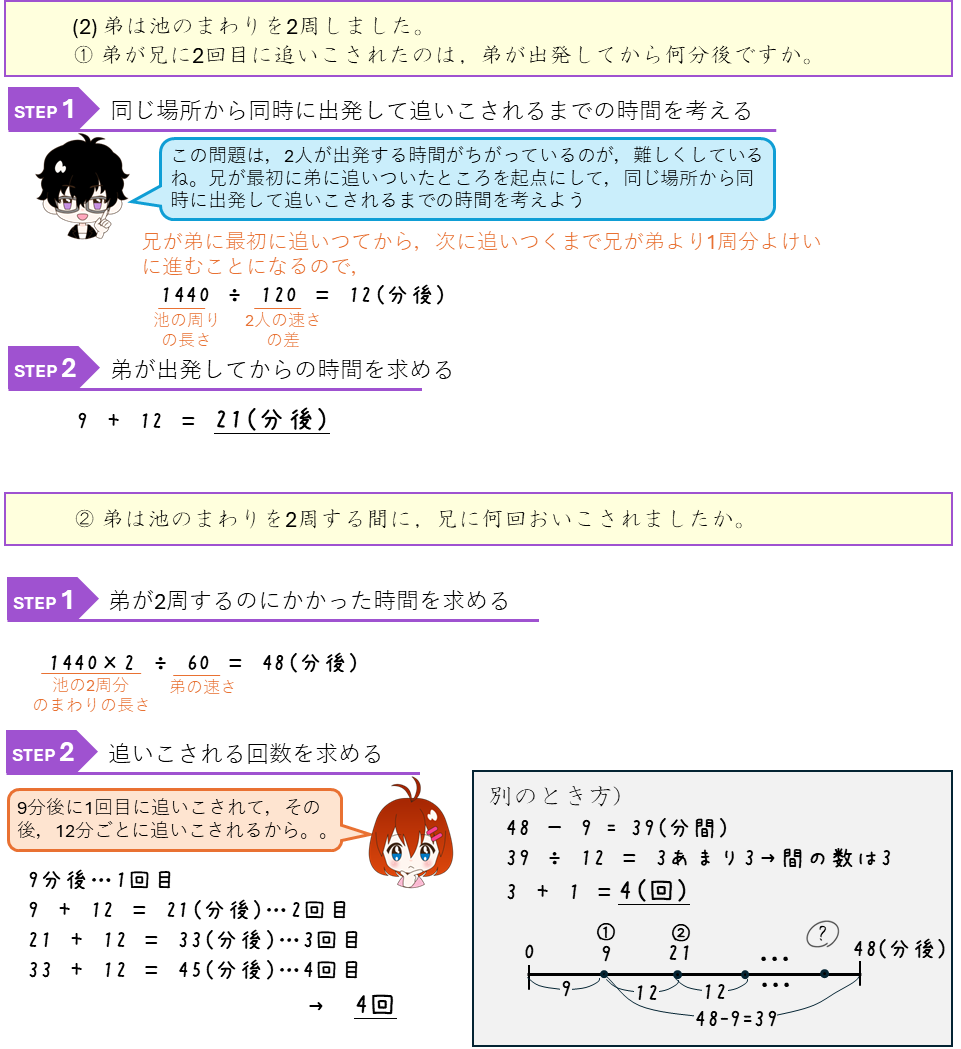
練習問題
円周上の旅人算
2人のきょりのグラフ
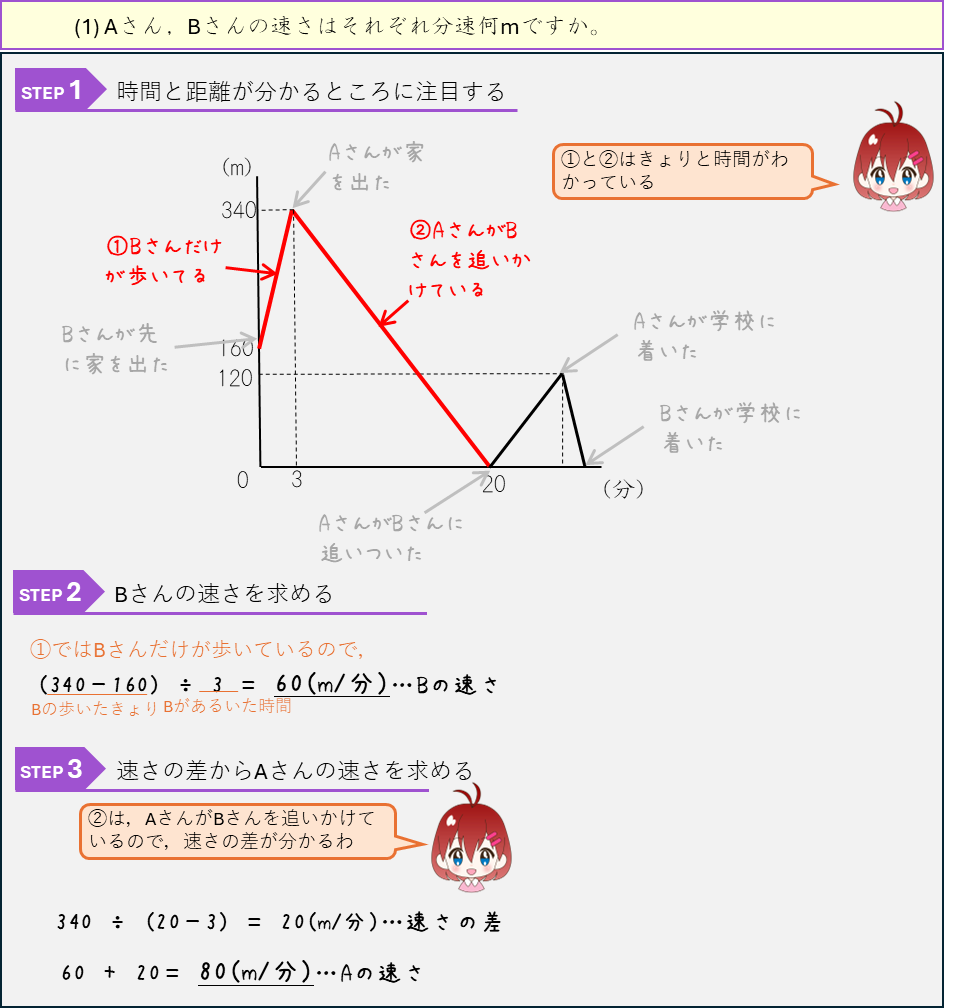
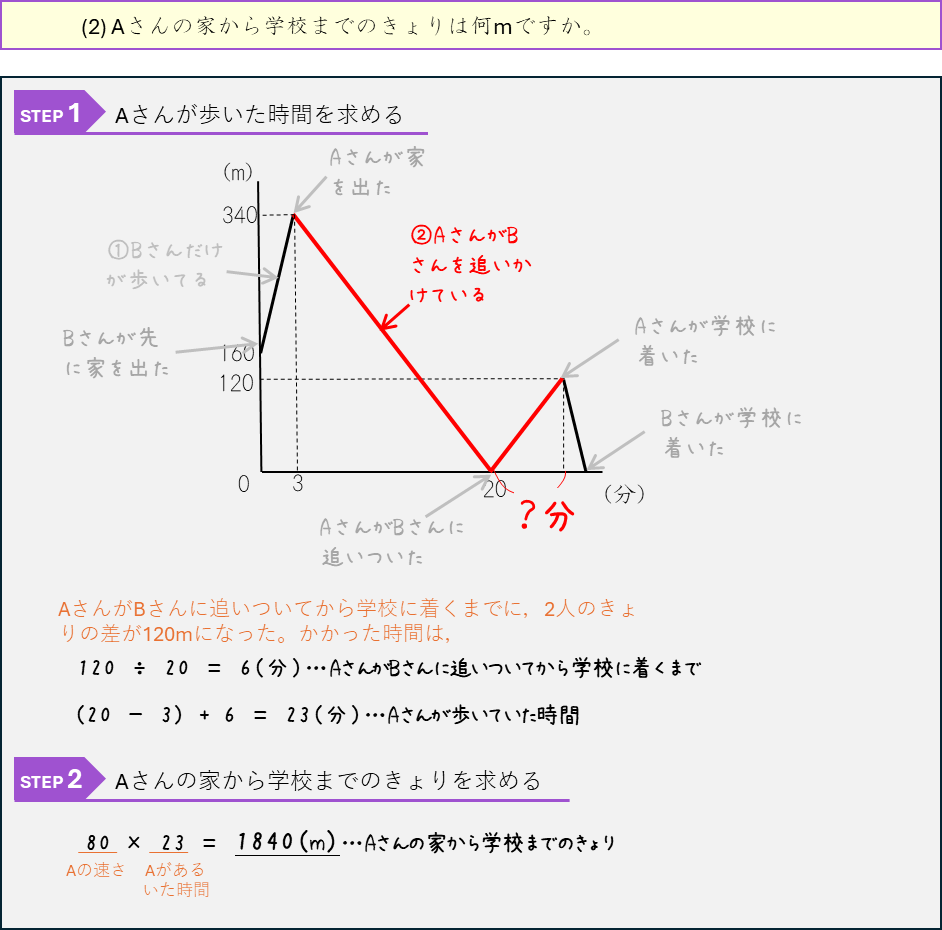
3人の旅人算ー直線コース
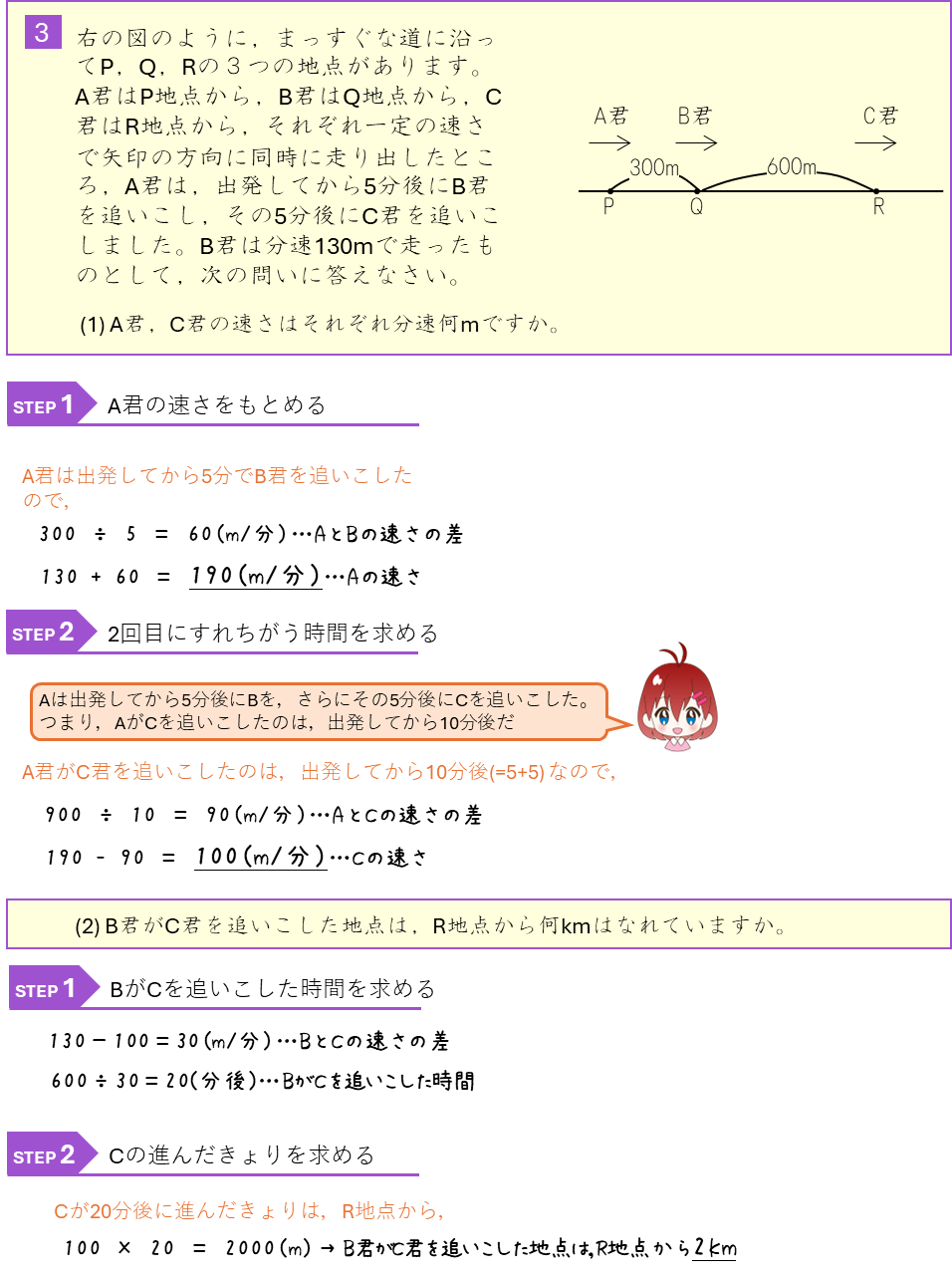
3人の旅人算ー円周コース
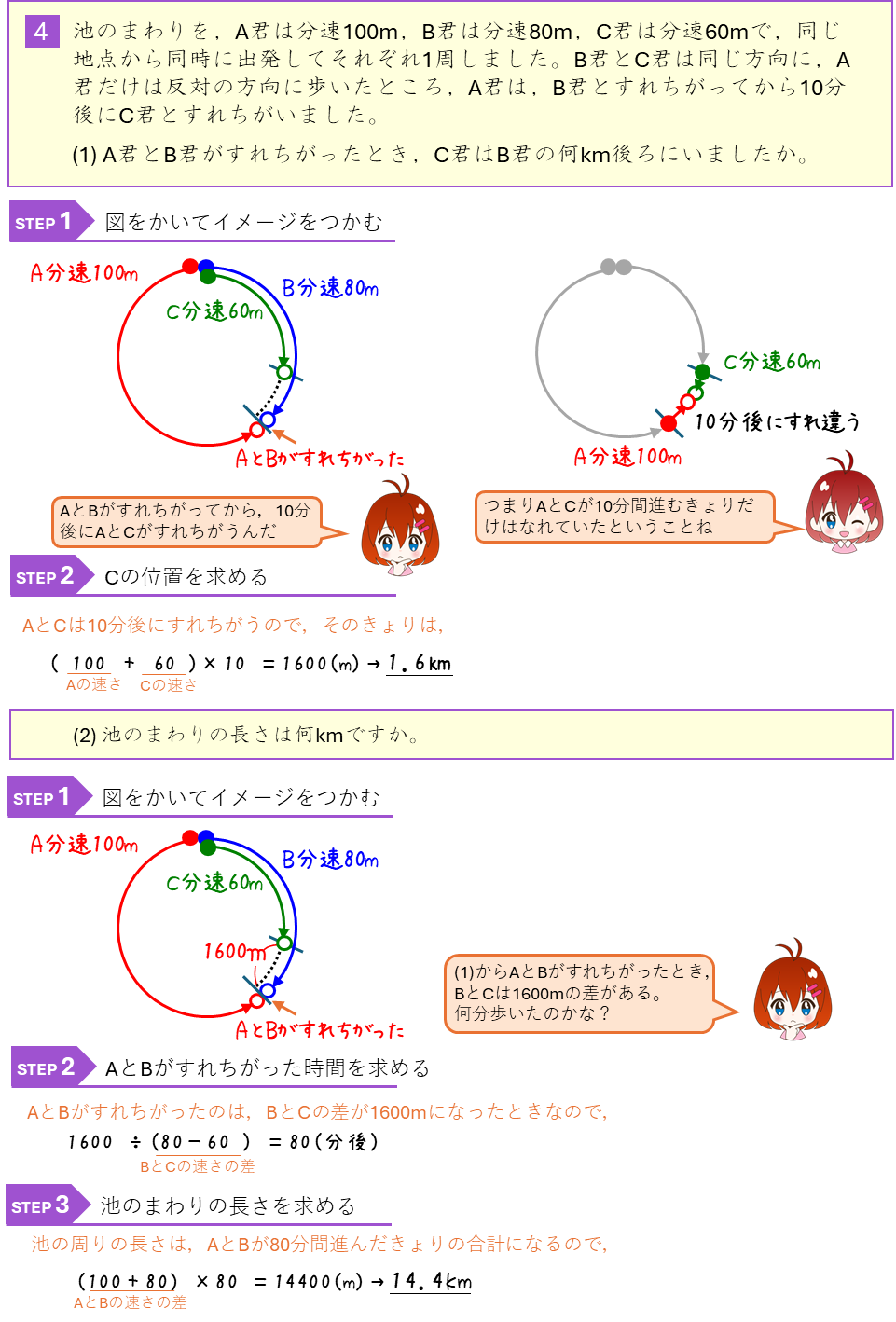
2人のきょりのグラフ

コメント