
この単元では、人などが進むようすを表したグラフなど速さに関連した応用問題を勉強していきます。進行を表すグラフは、ダイヤグラムとも言います。はじめは難しいかもしれませんが、グラフの読み方をしっかり理解できると、速さをイメージしてとくことができるようになります。また、つるかめ算を使った速さの問題もでてきます。不安があったらつるかめ算を復習しておきましょう。
(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説
今回は、速さのグラフに関する問題を解いていきます。速さの公式について、最初にまとめておくけど、これはちゃんと理解しているよね。
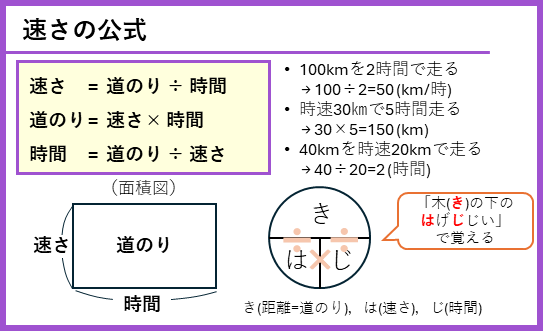
速さの公式
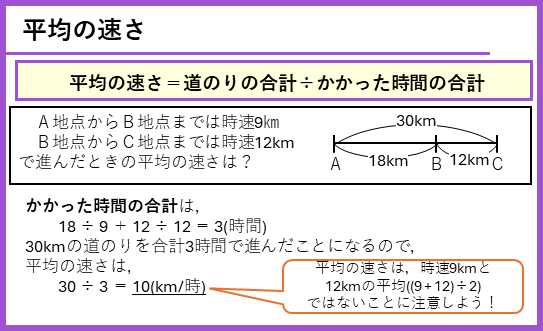
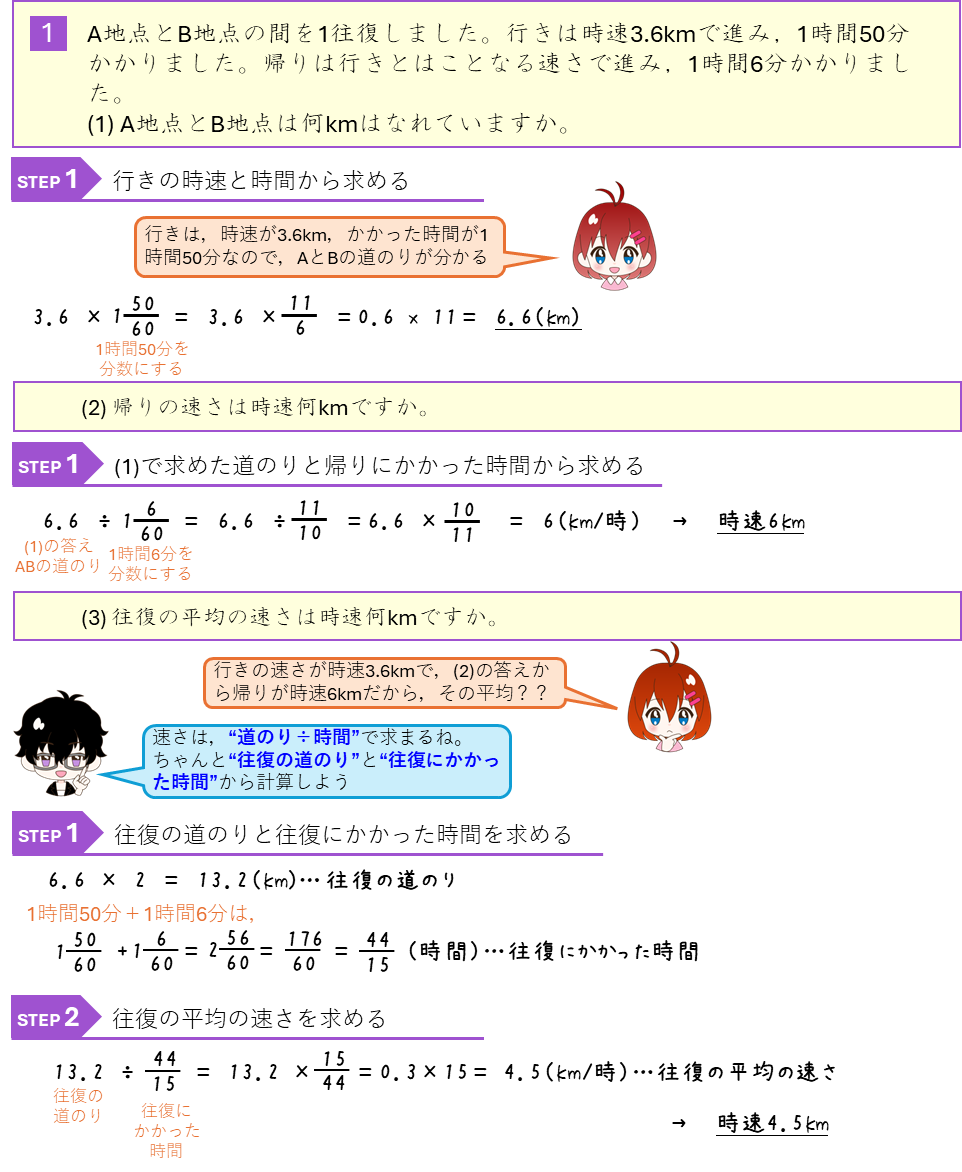
平均の速さ
平均の速さは、道のりの合計とかかかった時間の合計を求めて
平均の速さ=道のりの合計÷かかった時間の合計
で計算します。
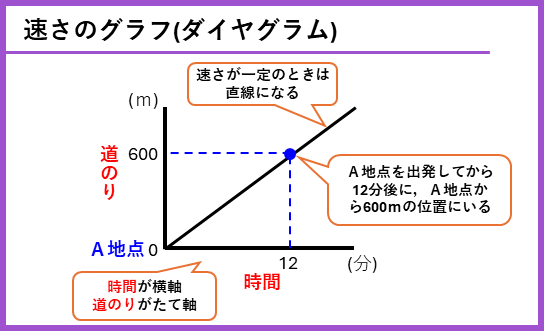
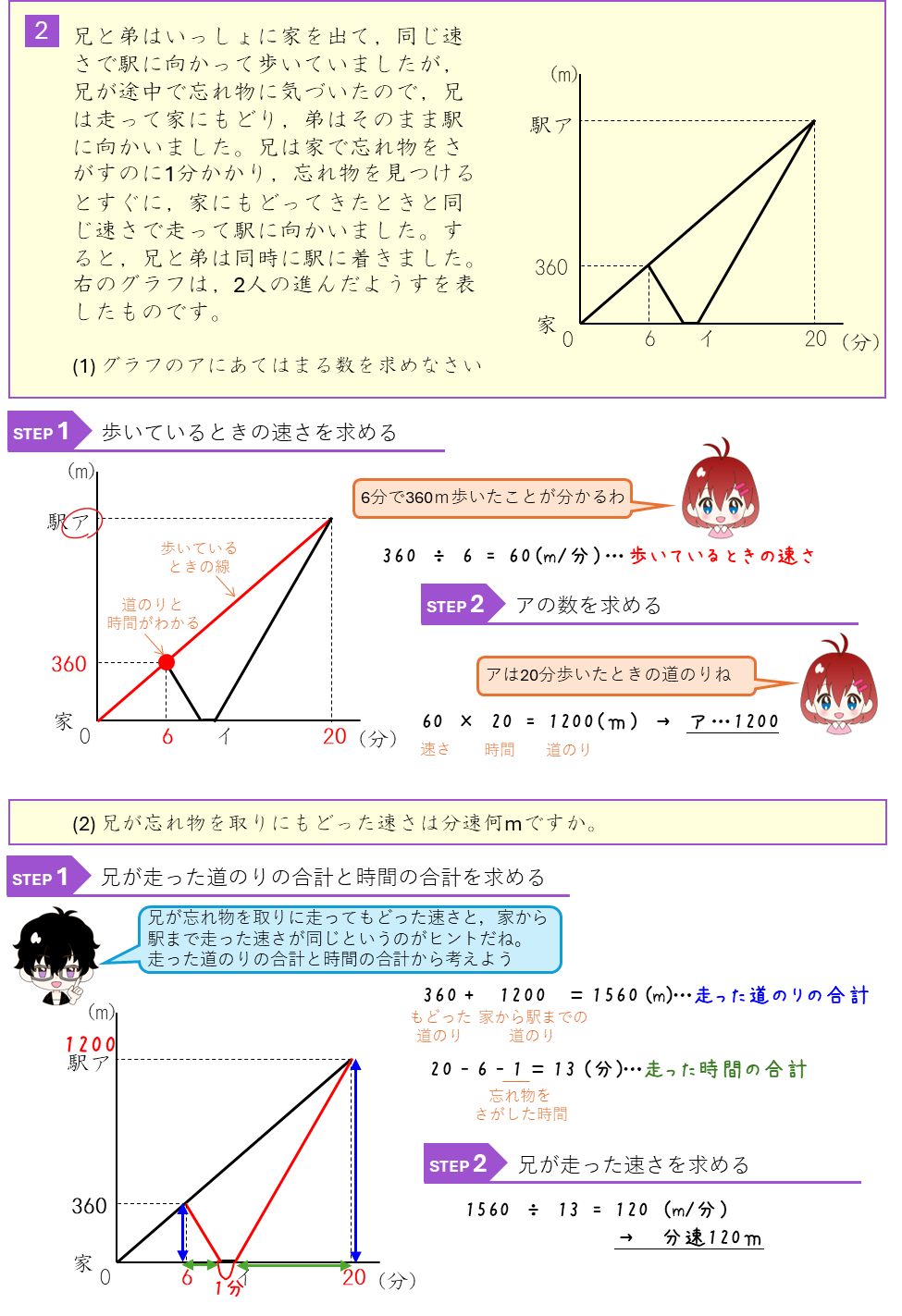
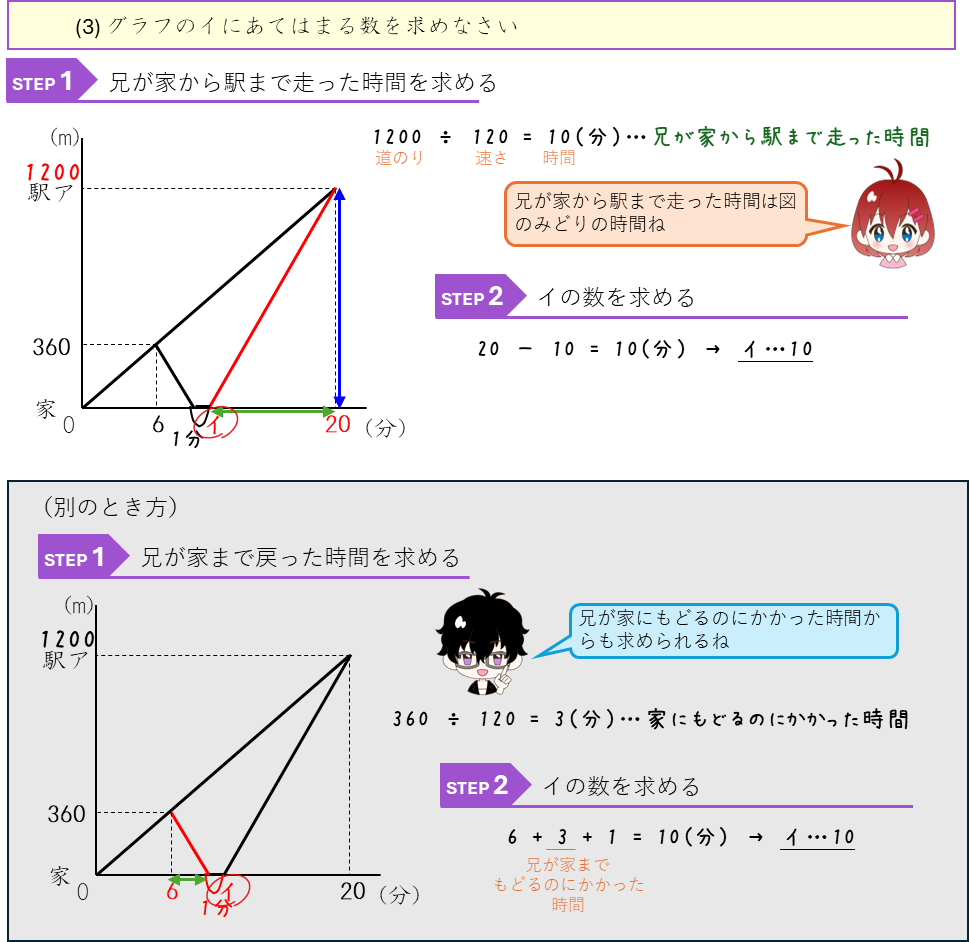
速さのグラフーダイヤグラム
今回新たに、人や車などが進むようすをグラフに表した問題を勉強します。この速さのグラフのことをダイヤグラムとも言います。グラフでは、グラフの縦じくが「道のり」で、横じくが「時間」を表していて、時間とともに人や車がどの位置へ進んでいるか分かります。はじめは少し難しく思うかもしれないけど、一度理解してしまえば、速さを図でイメージしてとくことができるよ。
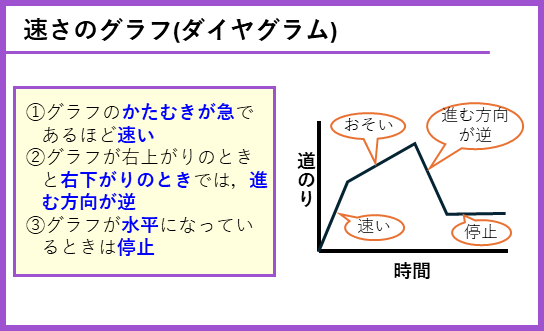
ダイヤグラムの性質をまとめておくのでそれぞれを確認しておきましょう。
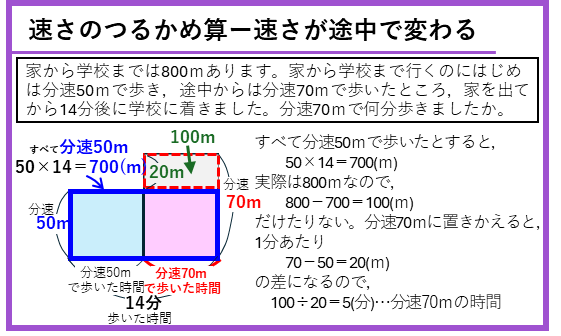
速さのつるかめ算ー速さが途中で変わる問題
速さが途中で変わる問題は、つるかめ算を使って解きます。2種類の速さが出てきたとき、すべてどちらか一方の速さで進んだとして道のりを計算して実際との差を考えて解いていきます。
練習問題
平均の速さ
ダイヤグラム
速さのつるかめ算
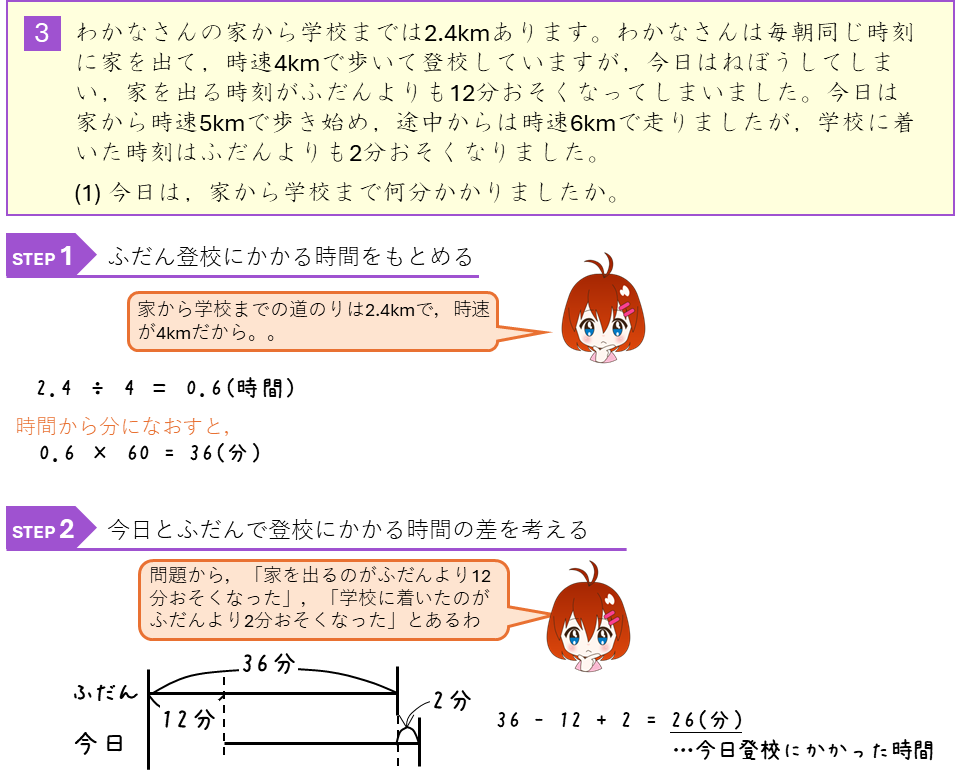
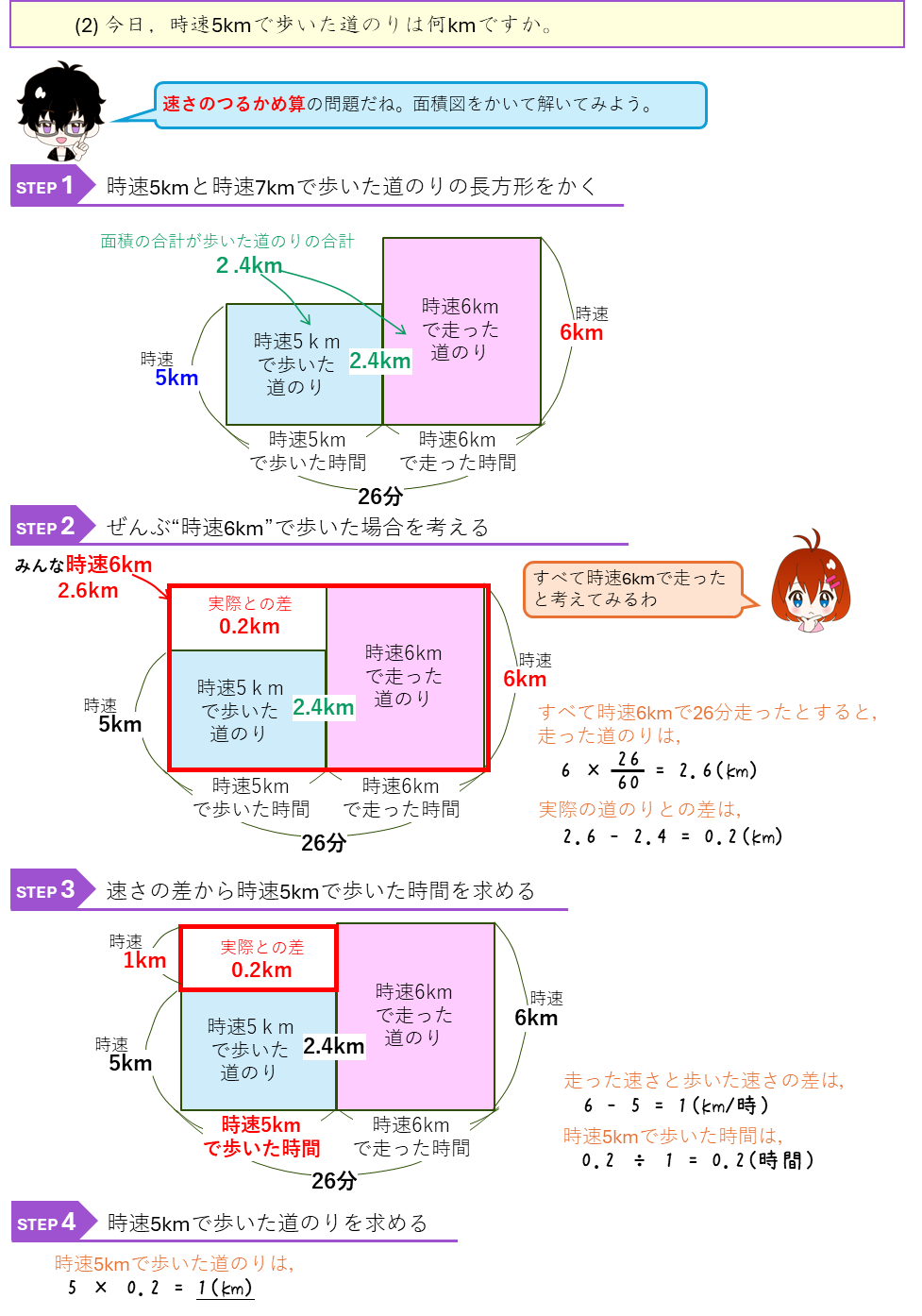
ダイヤグラムと速さのつるかめ算
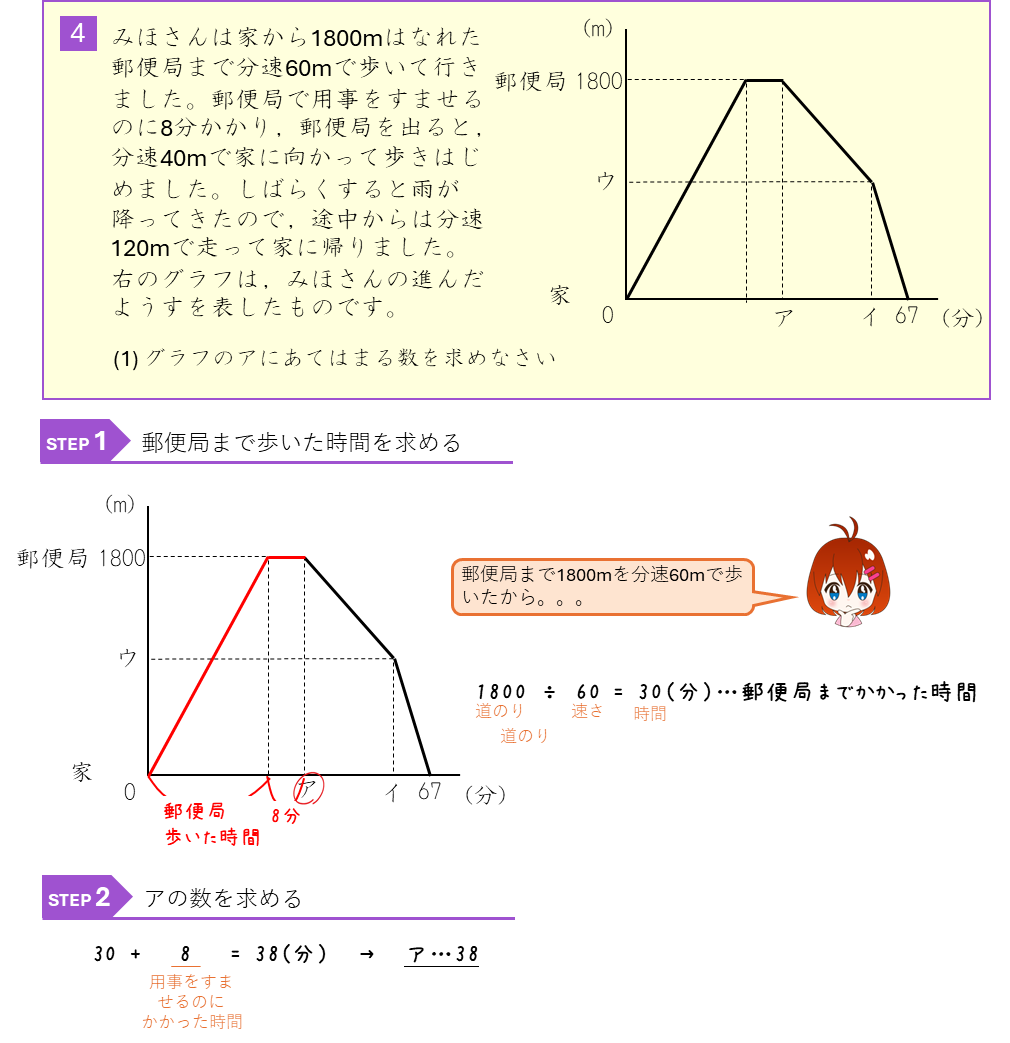
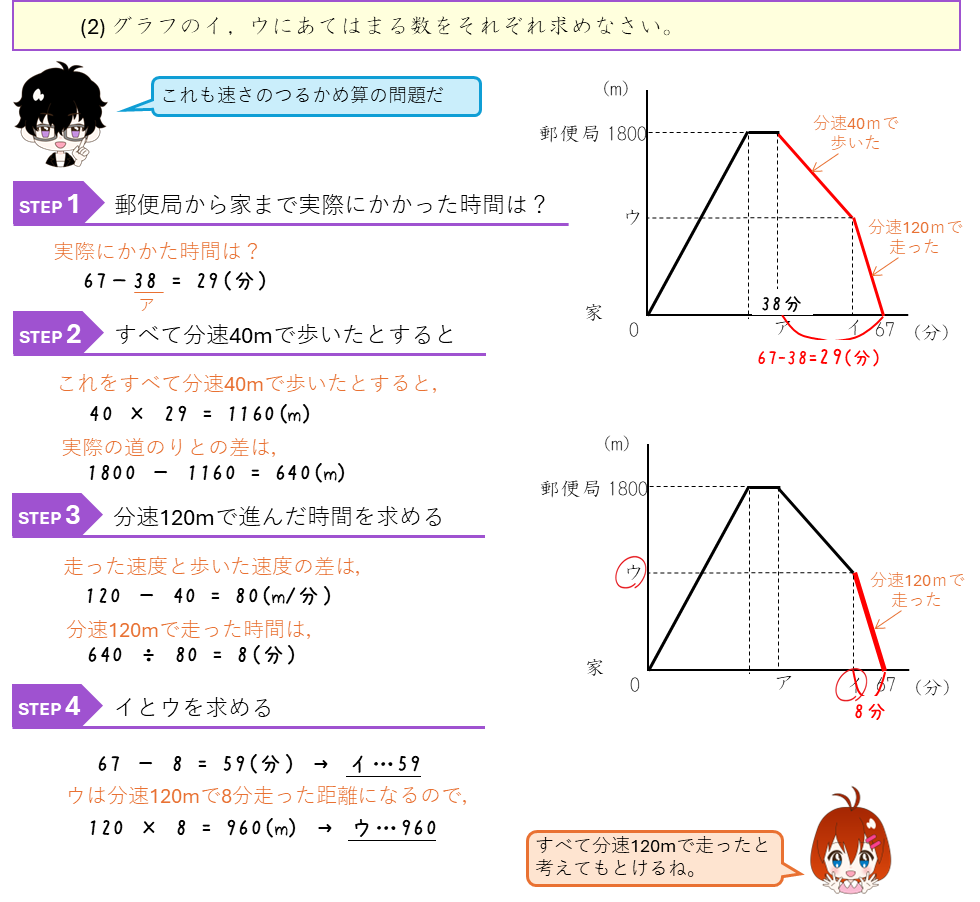
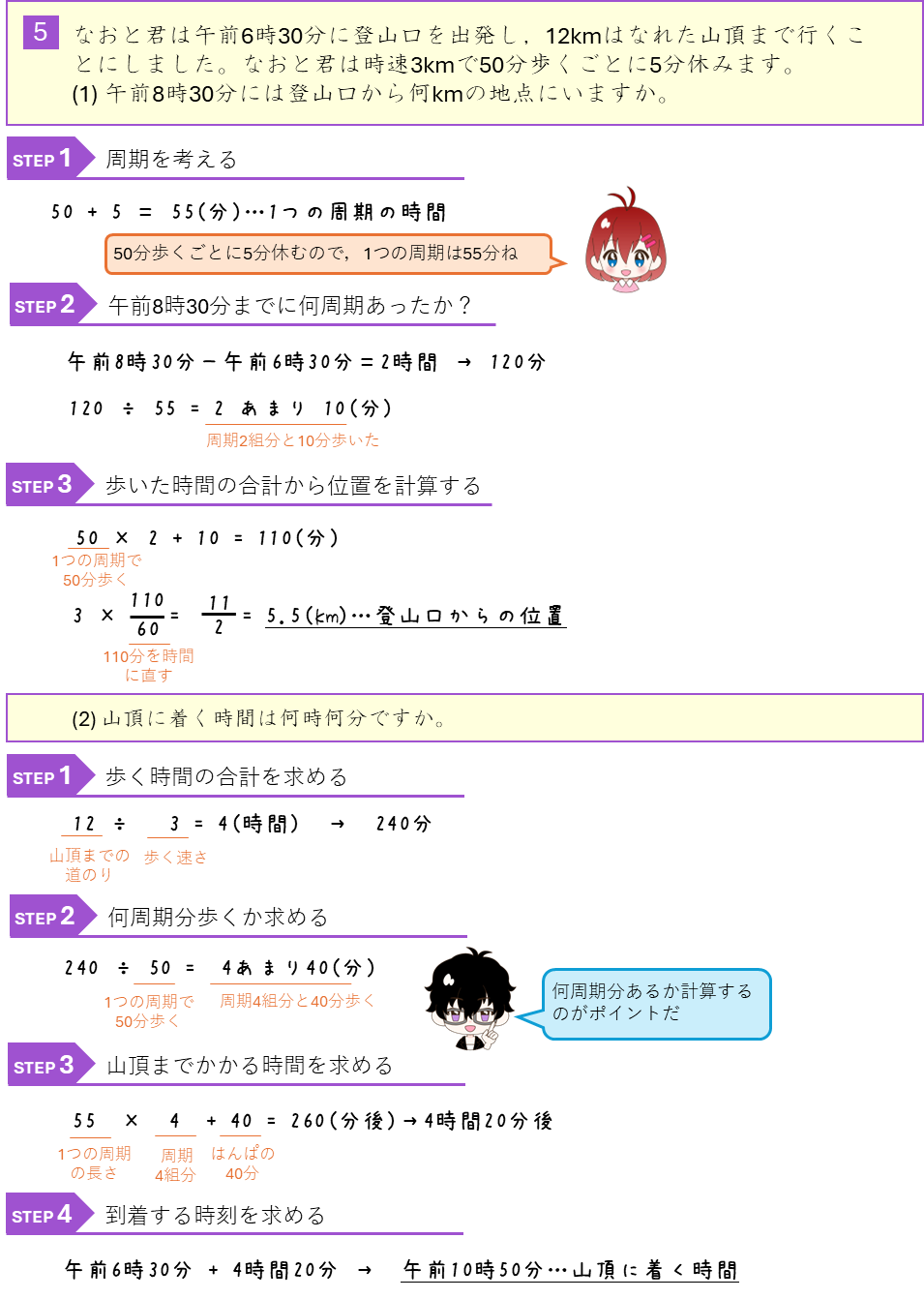
速さと周期

コメント