
5年生の授業が始まりました。上期の第1回は、「倍数と約数の利用」です。4年上の第16回「約数」と第17回の「倍数」の内容をさらに発展させた内容になっています。
あまり(あるいは、不足)がある数については、等差数列になることを利用します。また、周期の考え方を使う問題もあります。これらもすでに学習したものですが、倍数や約数との組み合わせになるので、必要に応じてこれらの単元も見直しましょう。
約数や倍数は、文章題などと違って数自体に関するものなので、イメージするのが難しいかもしれません。そのときは、線分図をかいてみてください。
(四谷大塚 予習シリーズ算数 五年上の解説です。テキストは四谷大塚から購入してください。)
解説
約数の復習
4年上の第16回「約数」の復習です。
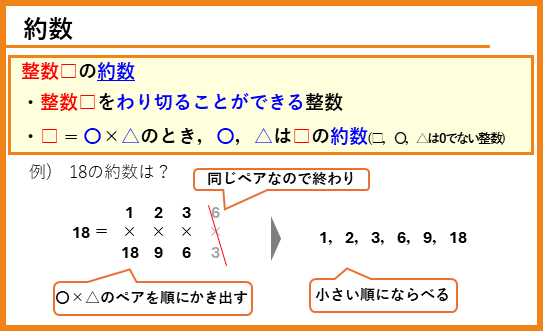
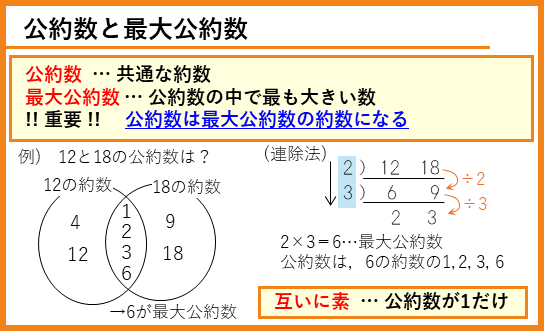
倍数の復習
4年上の第17回「倍数」の復習です。
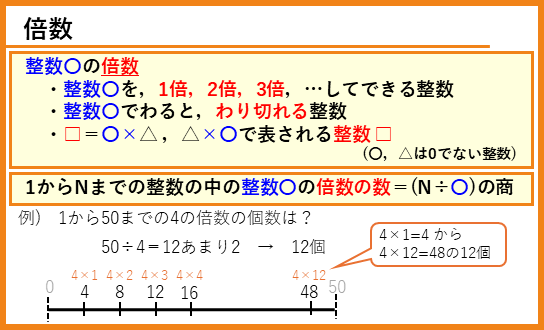
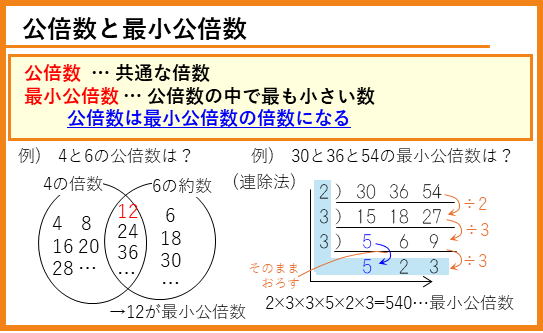
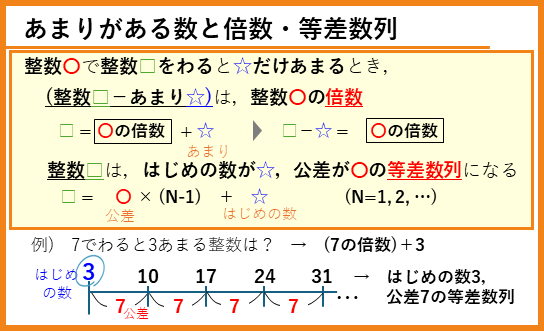
あまりがある数ー倍数と等差数列
整数〇で整数□をわると☆だけあまるとき,
(整数□-あまり☆)は,整数〇の倍数
になります。また、整数□は,はじめの数があまり☆,公差が〇の等差数列になります。

例えば、
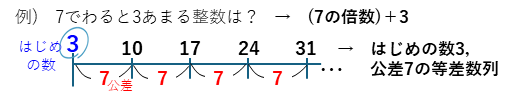
となります。
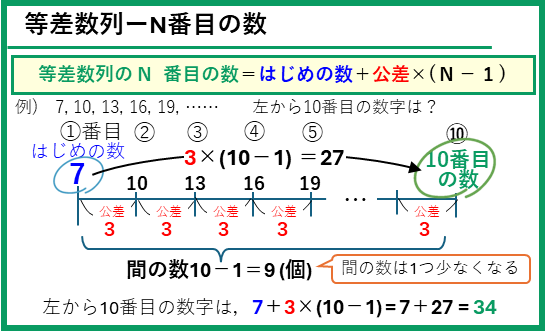
等差数列であることが分かれば、その公式を使って、N番目の整数□の値や、100や1000などの数に最も近い整数□の値などを求めることができます。
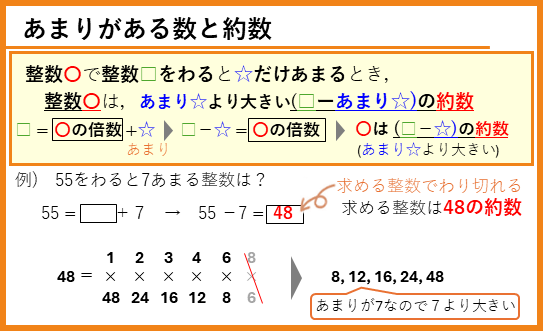
あまりがある数ー約数
整数〇で整数□をわると☆だけあまるとき,
(整数□-あまり☆)は,整数〇の倍数
ですが、倍数と約数の関係から、逆に
整数〇は,(整数□ーあまり☆)の約数
になっています。ここで注意が必要なのは、整数〇はあまり☆より大きいということです。問題を解くとき、このことを忘れないようにしましょう。
例えば、
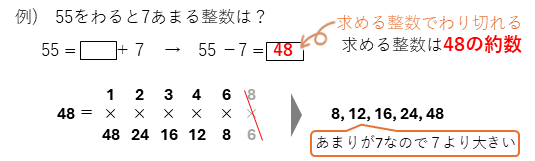
となります。
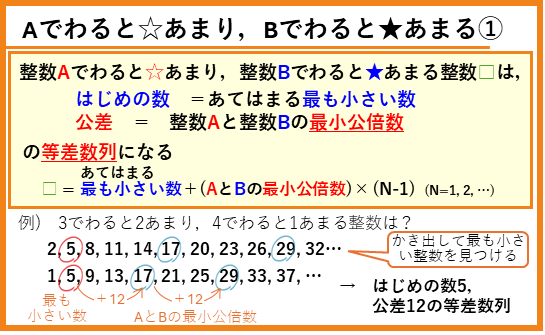
Aでわると☆あまり,Bでわると★あまる
整数Aでわると☆あまり,整数Bでわると★あまる整数□は,
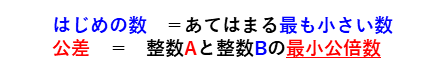
の等差数列になります。

例をあげると、

となります。この例では、3でわると2あまる整数と、4でわると1あまる整数を小さいものからかき出して、最も小さい数を求めます。そのあとは、3と4の最小公倍数12が1つの周期となり、くり返しあらわれることがわかります。
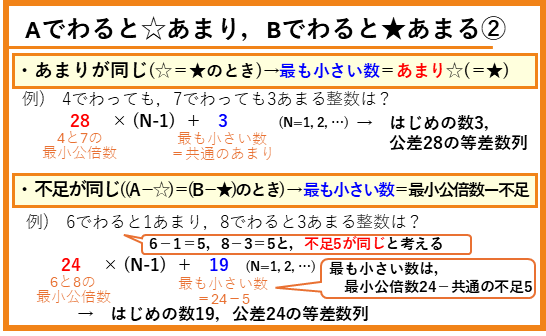
あまりが同じ場合や不足が同じ場合では、かき出さないでもあてはまる最も小さい数(はじめの数)が分かります。
あまりが同じ
あまりが等しいときは、あてはまる最も小さい数は、あまりになります。

不足が同じ
不足(わる数からあまりをひいた値)が等しいときは、あてはまる最も小さい数は、
2つの数の最小公倍数-不足
となります。

順にかき出してあてはまる最も小さい数を求めても解けますが、かき出すのが大変な場合もあります。この2つの場合は、覚えておくと素早く解くことができます。
同じ数でわると、あまりが等しい
整数〇で整数□と整数△をわると,あまりが等しくなるとき(□÷〇と△÷〇のあまりが等しいとき)、□と△の差を、〇でわり切ることができます。つまり、〇は,□と△の差の約数となります。
例えば、次の例題を考えてみます。

線分図をかいて考えると、以下のようになります。
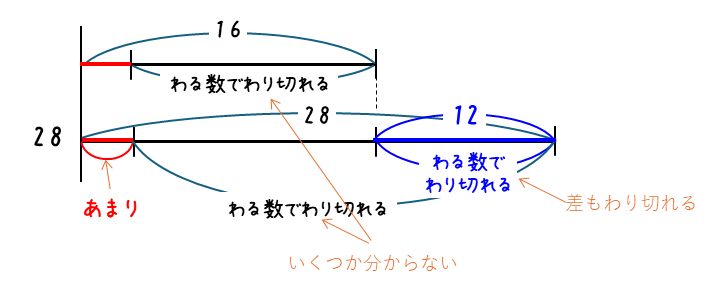
16からあまりをひいた数や、28からあまりをひいた数は、あまりの数が分からないので、いくつか分かりません。しかしながら、16と28の差は12と計算でき、さらに、この差もわる数でわり切れます。したがって、わる数は、差の12の約数となります。
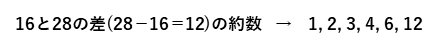
これらすべてが答えではなくて、このうち、あまりが1以上となるものだけが答えです。したがって、
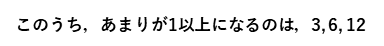
となります。このように差もわり切れることがポイントですので、これを理解して、覚えておきましょう。
まとめ
今回の内容をカードにまとめます。

練習問題
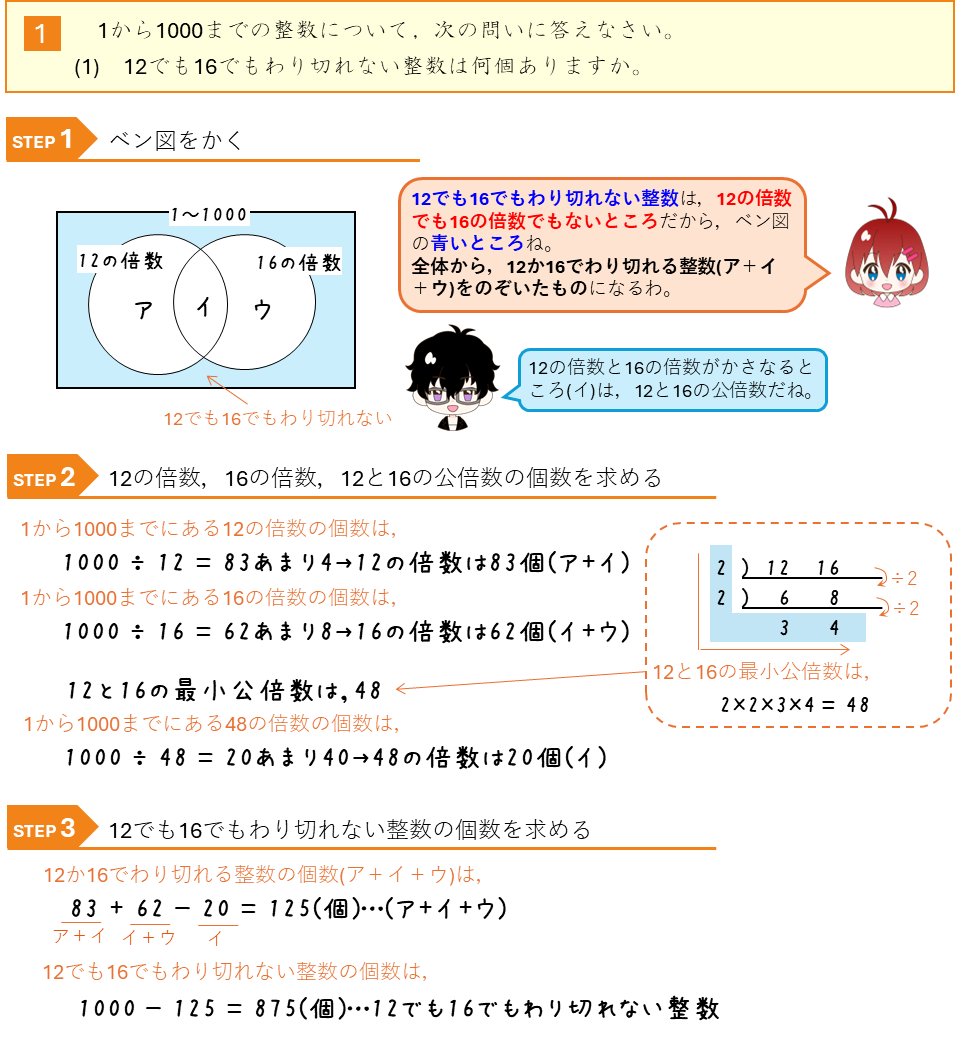
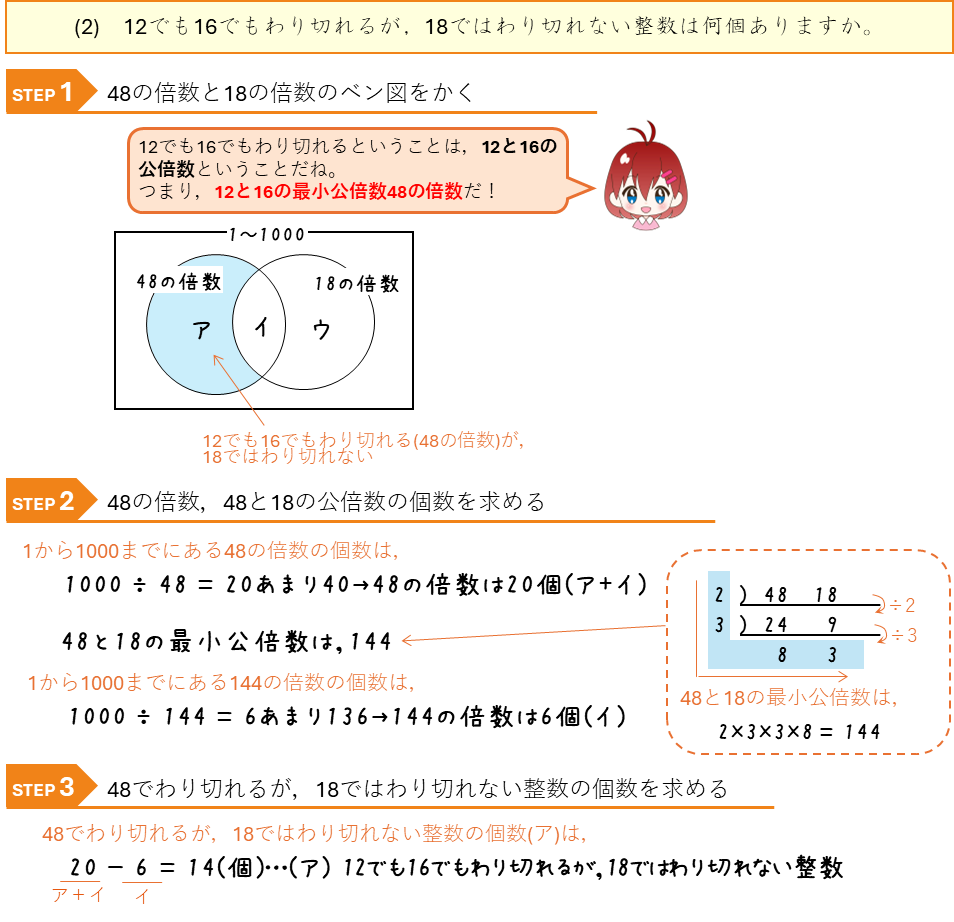
倍数ーわりきれる整数とわり切れない整数の個数
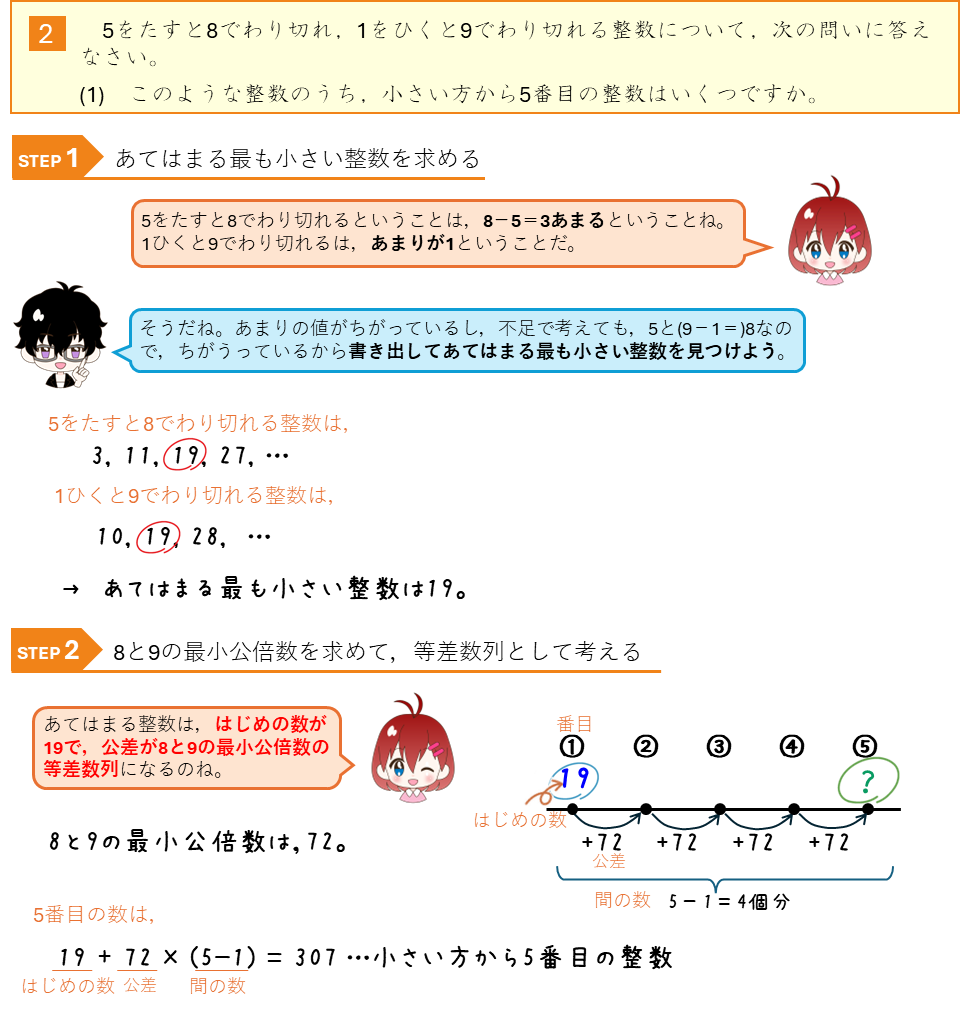
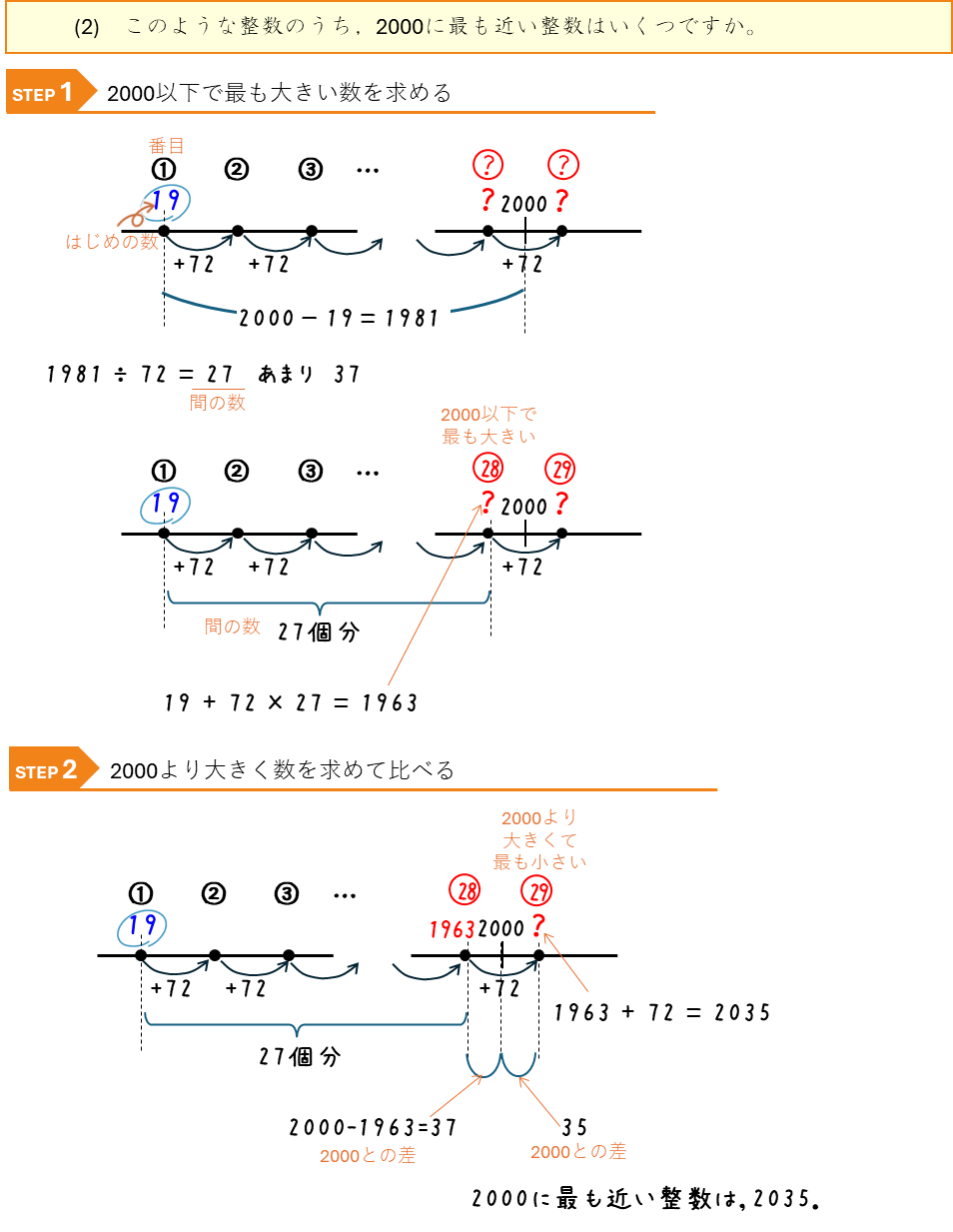
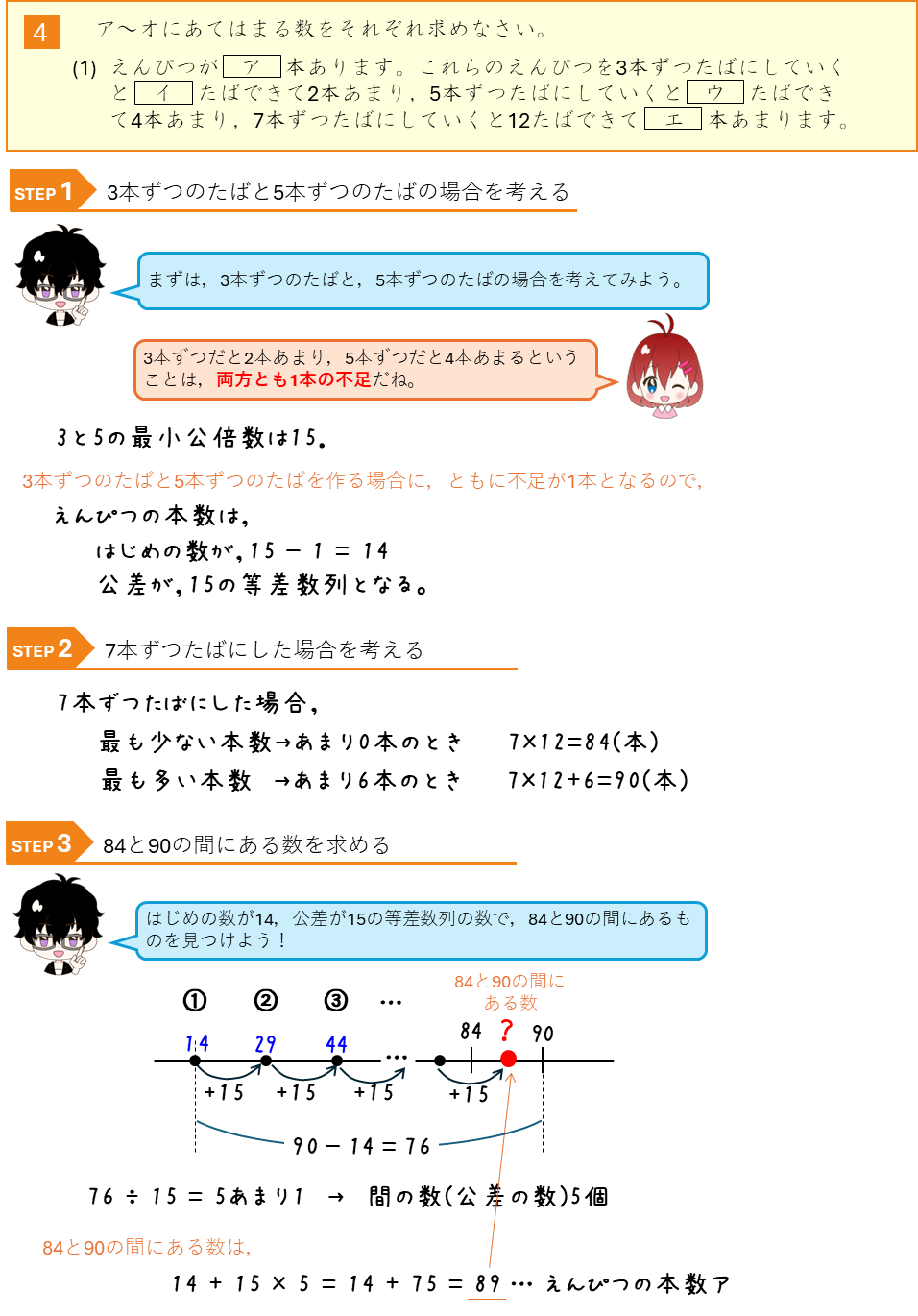
わり算のあまりと等差数列ー不足とあまり
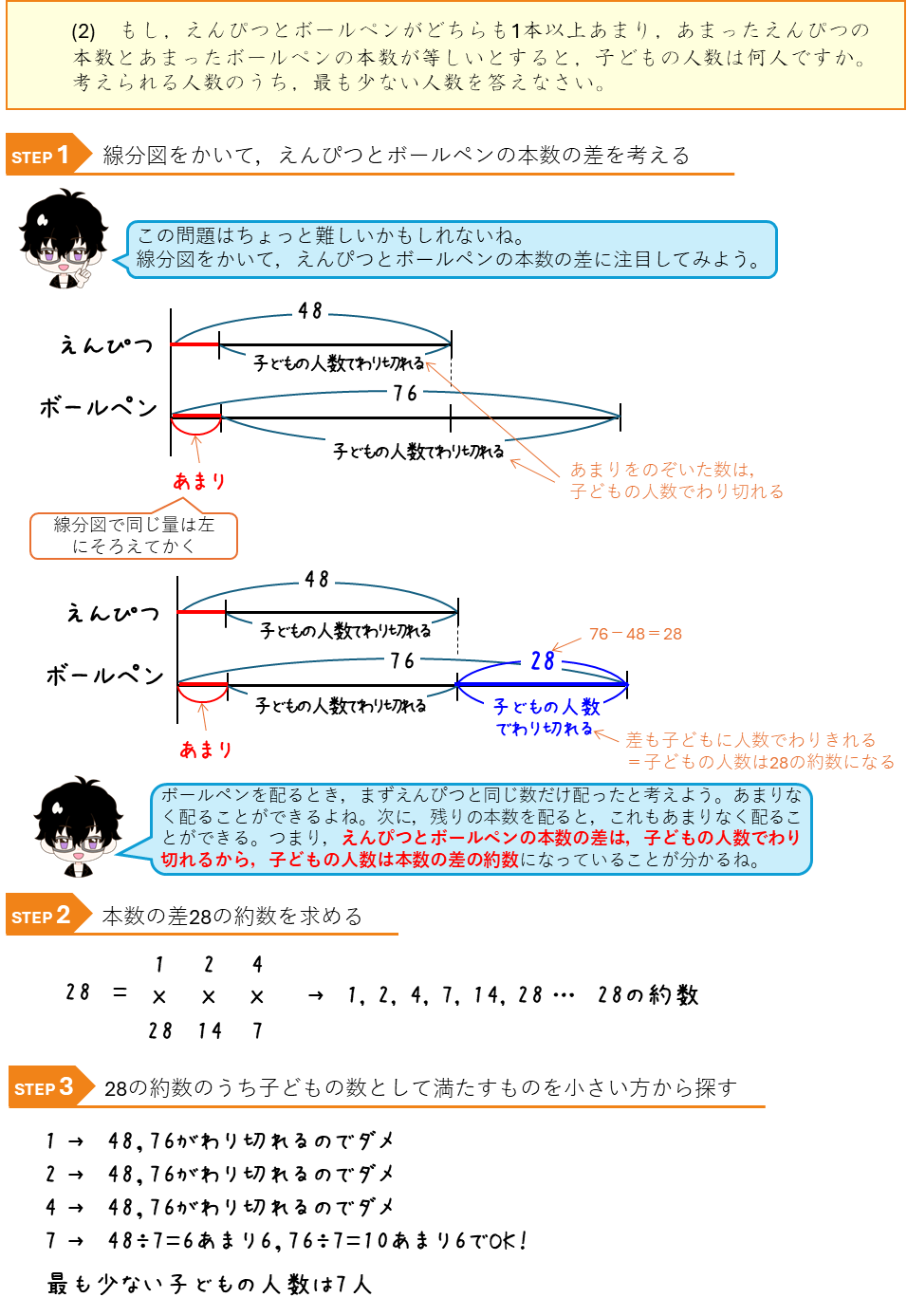
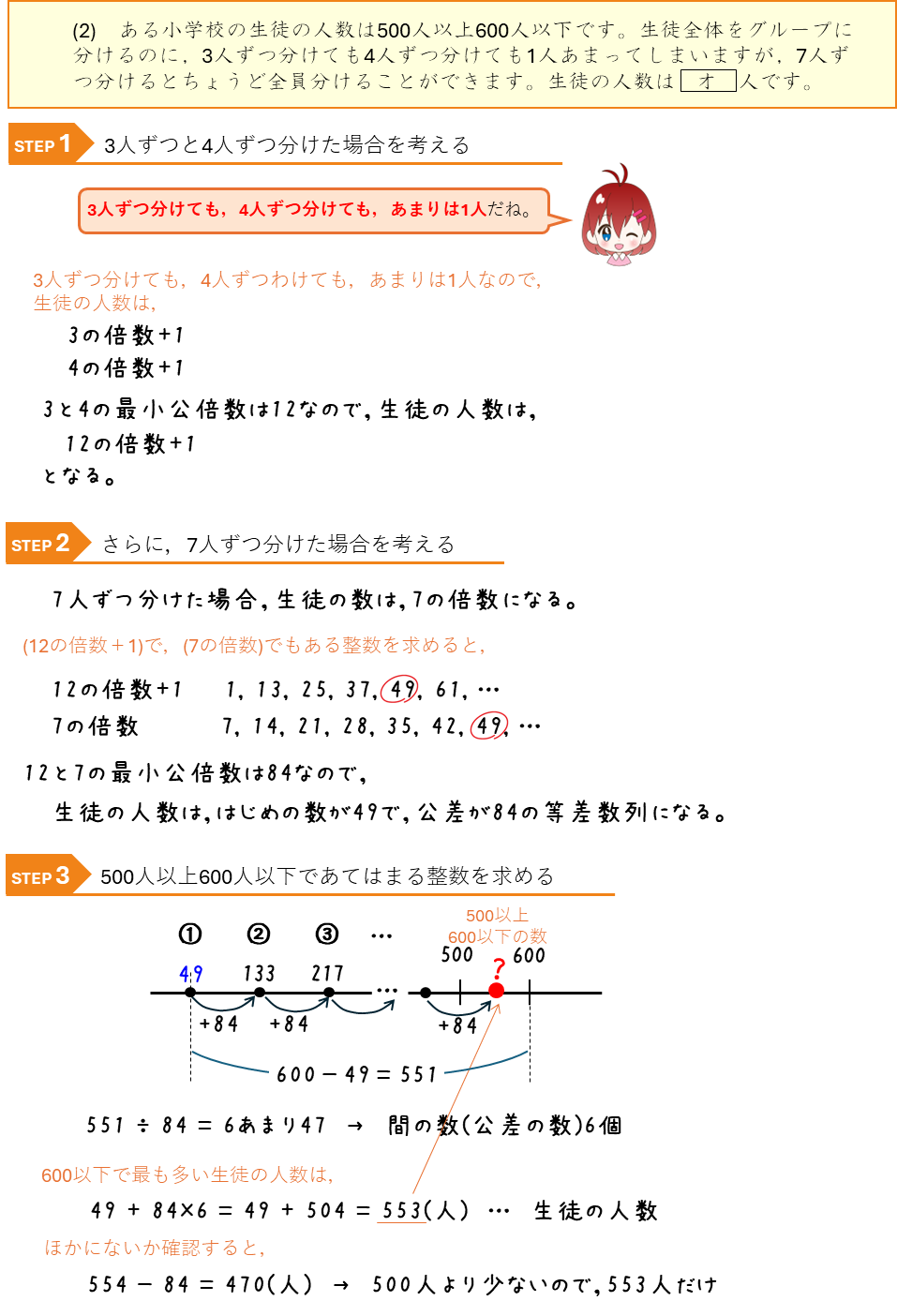
公約数ーえんぴつとボールペンを配るとあまりがでる

わり算のあまりと等差数列ー3つのパターンでわる

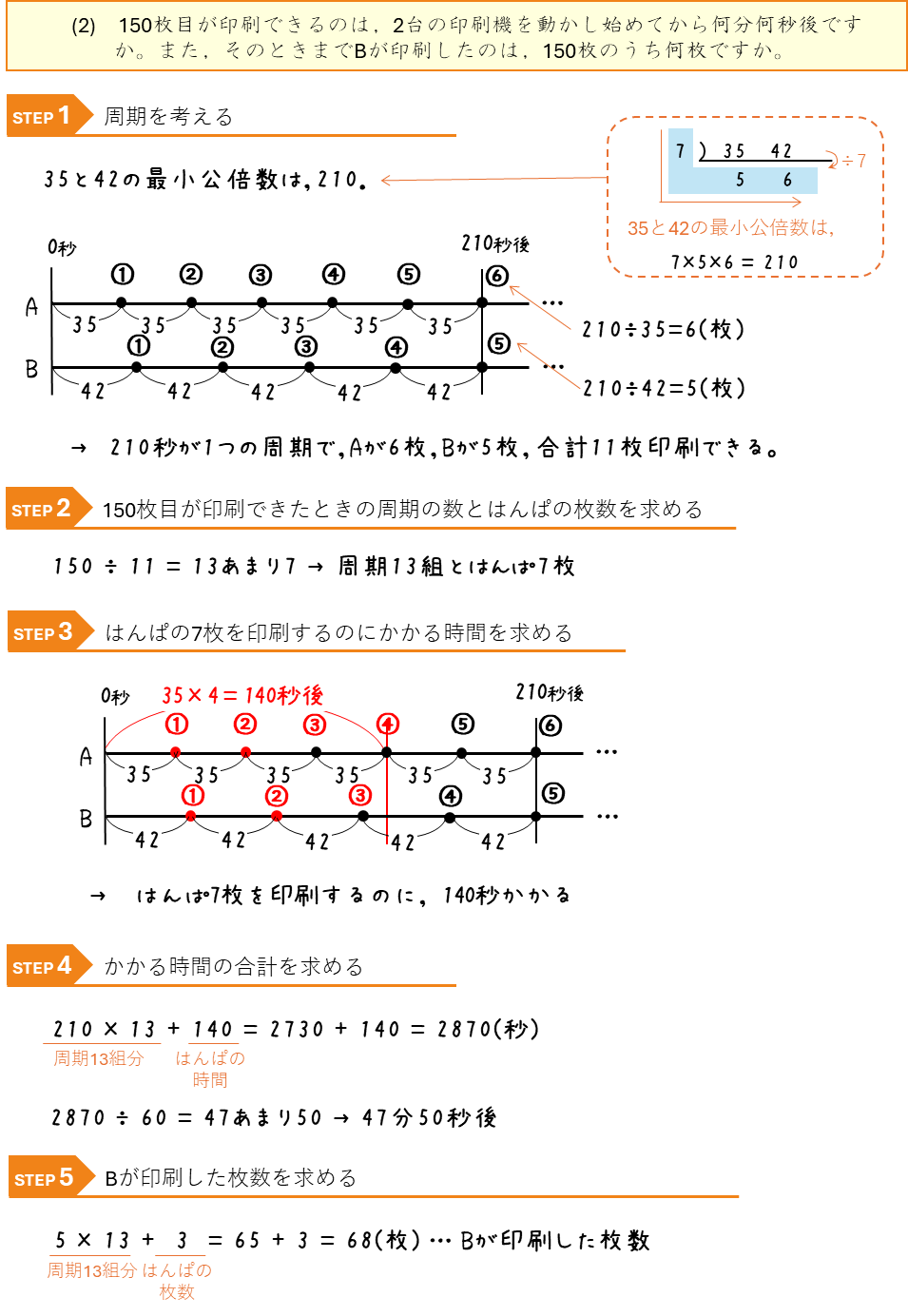
周期算ー2台の印刷機で印刷できる枚数

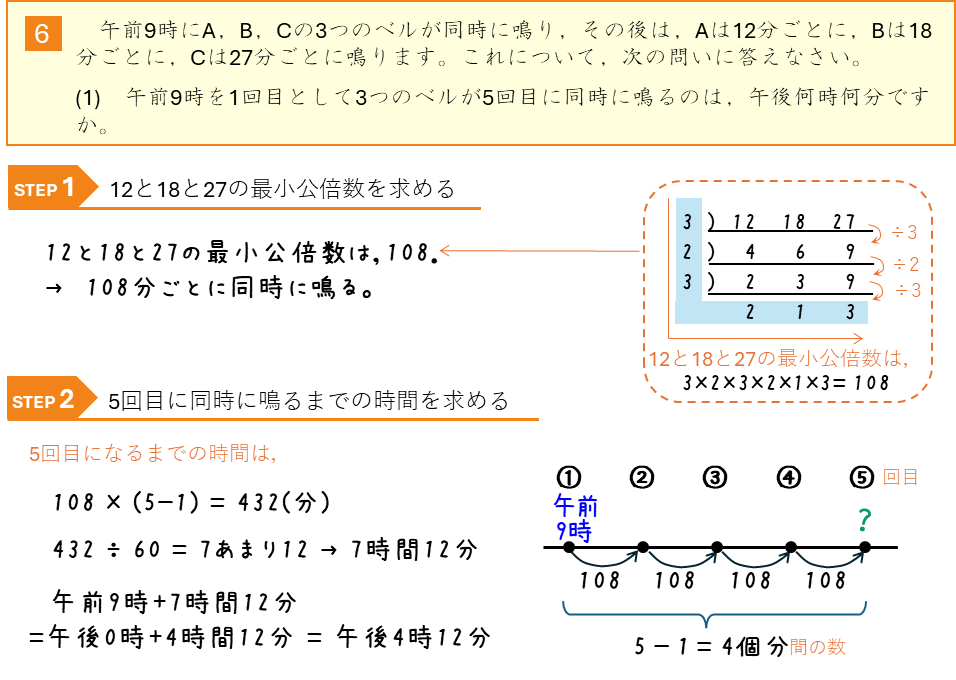
周期算ー3つのベルが鳴る
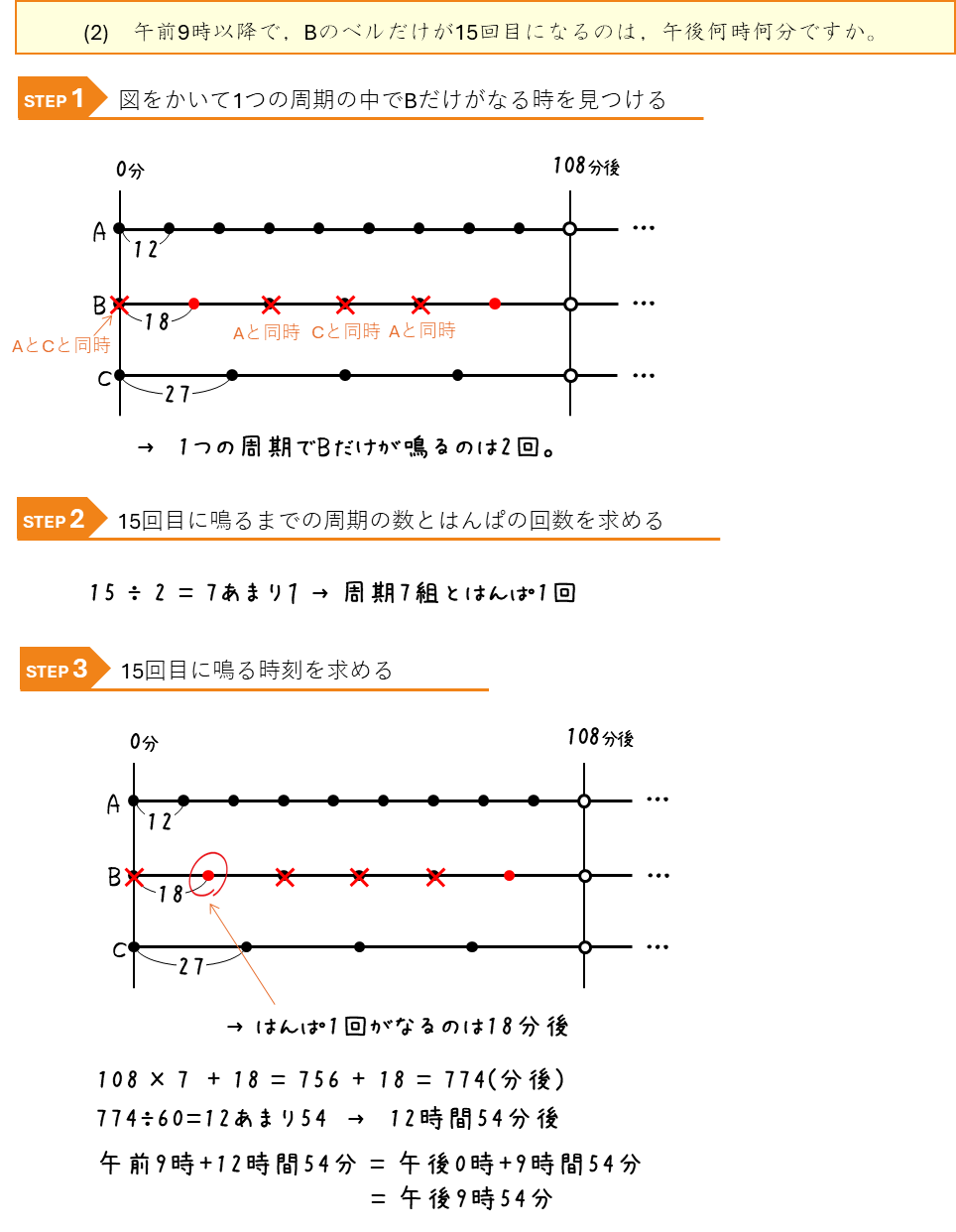



コメント