
今回は、「割合」について勉強します。
割合と5年生で習う比を苦手とする人が多いようです。「割合」を簡単に言うと、「AはBの何倍」の「何倍」のことです。
「くらべる量」、「もとにする量」という新しい言葉と「割合の3つの用法の公式」が出てくるので、単に公式を丸暗記するだけだと難しく感じてしまい、苦手になってしまうようです。ここでは、「もとにする量の見つけ方」や「暗記方法」も覚えていきましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
割合とは
割合とは,「もとにする量を1としたとき,くらべる量がどれだけにあたるか 」を表すものです。この言葉だけだと分かりづらいので、「AはBの何倍」の何倍が割合です。
例1) Aが10で、Bが5です。Bを1としたとき、Aの割合は?(AはBの何倍?) → 10÷5=2
例2) Aが4で、Bが10です。Bを1としたとき、Aの割合は?(AはBの何倍?) → 4÷10=0.4
例3) Aが5で、Bが13です。Bを1としたとき、Aの割合は?(AはBの何倍?)→ 5÷13=$\frac{5}{13}$
例2や例3のように、何倍といっても、割合が小数や分数になる場合があるので、慣れておきましょう。
割合の3用法
割合の式には、割合、くらべる量、もとにする量の3つが出てきます。それぞれを求める問題が出題されるので、その公式をまとめていきます。
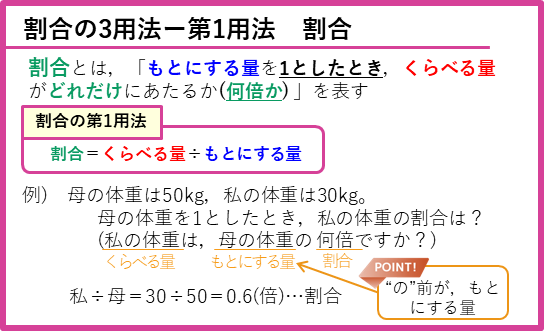
第1用法 割合を求める公式 …「母の割合」
まずは、割合を求める公式です。次の例を考えます。


この問題で、「母の体重を1としたとき」とあるので、母の体重が「もとにする量」になります。この問題を言いかえると、

となります。この問題文での、くらべる量、もとにする量、割合は、

です。「母の体重の」の「の」の前の「母の体重」がもとにする量です。「の」の前がもとにする量ということを覚えておきましょう。

この問題の答えは、私の体重が30kgで、母の体重が50kgなので、
私 ÷ 母 = 30 ÷ 50 = 0.6(倍)…割合
で求まります。これを割合の第1用法の公式の、

となります。「割合はもとにする量でわる」をしっかり覚えましょう。
わり算を分数で表すと、”の”の前の”もとにする量が分母”になるので、「”母の”割合」という言葉で一緒に覚えてしまいましょう。もとにする量が母というのも、なんとなくイメージに合いますね。

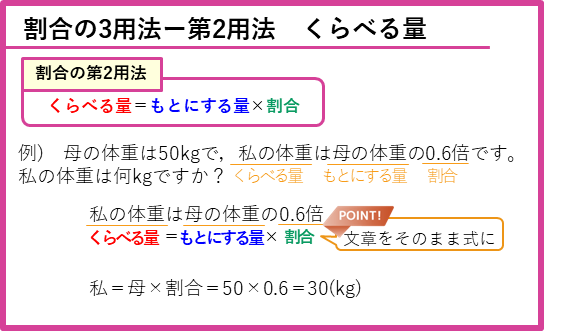
第2用法 くらべる量を求める公式
次は、くらべる量を求める公式です。

問題文の

を、”は”を”=”に、”の”を”×”に変えることで、そのまま式にすることができます。

これが、くらべる量を求める第2用法の公式です。

したがって、この例題は、
私 = 母 × 割合 = 50 × 0.6 = 30(kg)
で求めることができます。第2用法のポイントです。

第3用法 もとにする量を求める公式
最後の3番目は、もとにする量を求める公式です。これが一番わかりづらい公式です。
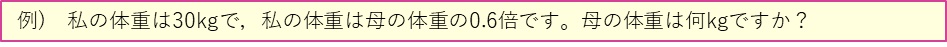
問題文の、

から、

となり、この問題は、母の体重、つまり、もとにする量を求めるものです。割合が0.6倍と小数になっているのが、さらに分かりづらくしています。

と言う問題であれば、母の体重は私の半分ということがイメージできるので、
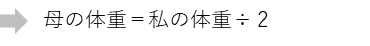
と、割合の2でわればよいことがすぐ分かると思います。同じように割合が小数や分数の場合も「もとにする量は、くらべる量を割合でわる」ことで求めます。
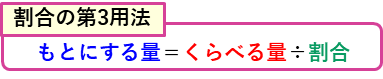

やはり、1より小さい数で割るというのはイメージしづらいのですが、結果の2人の体重を比べてみると、
私(30kg) < 母(50kg)
となっています。「1より小さい数でわった結果はもとの数より大きくなる」ことから、母の方が重いから、(1より小さい)0.6でわるので正しいと確認するのもいいと思います。
また、この計算を線分図をかいてイメージをもつこともできます。
線分図
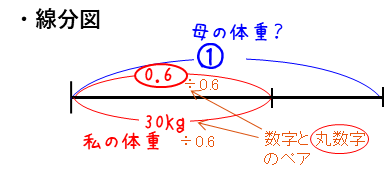
線分図をかいて、実際の数字と丸数字のペアを作ります。この例で丸数字の(0.6)を0.6でわると①になるので、同じように30kgを0.6でわれば、①のあたる量を求めることができます。
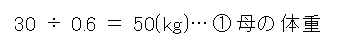
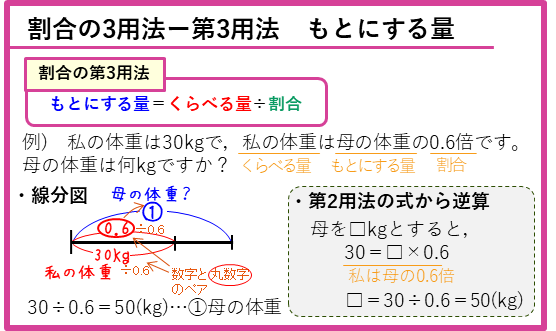
第2用法の式から逆算で解く
あるいは、式を立てるのが簡単な、くらべる量を求める第2用法から逆算で解くこともできます。

割合のポイントまとめ
以上、割合のポイントをまとめておきます。
・もとにする量を問題文から見つけられるようにしましょう。

・割合は、もとにする量でわります。

この2つは、「母の割合」と言って、一緒に覚えてしまいましょう。

・くらべる量は、文章をそのまま式にします。


・もとにする量は、割合でわります。
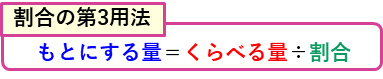
この公式に自信がない場合は、線分図をかいて考えたり、第2用法から逆算で求めるなどしてください。
まとめのカード
練習問題
割合ーくらべる量と割合を求める

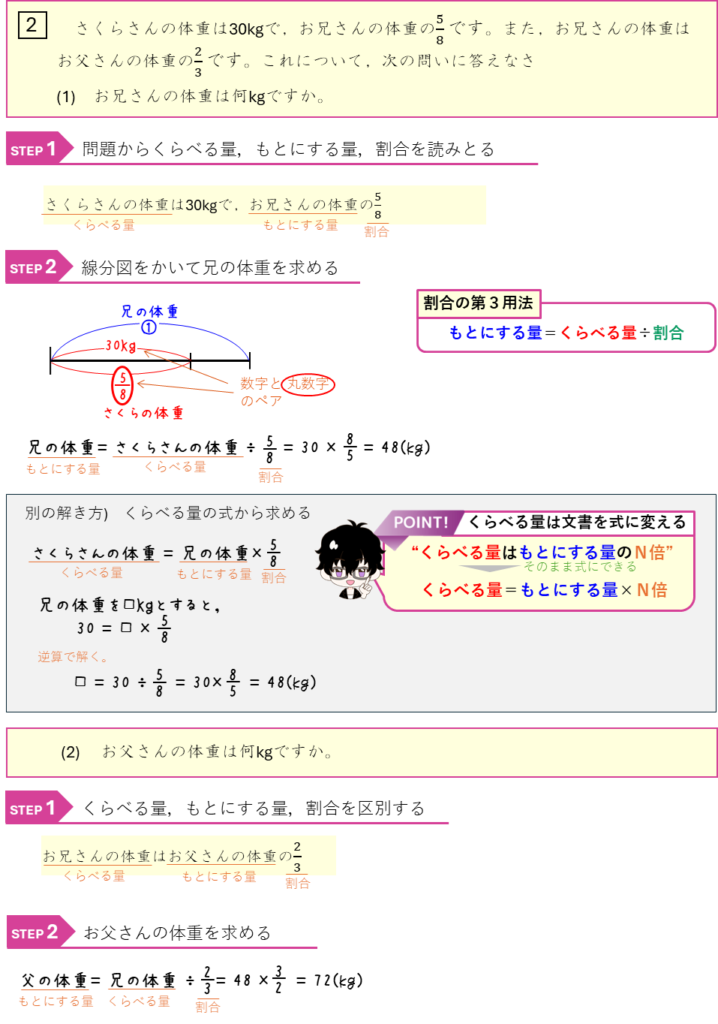
割合ーもとにする量・割合を求める

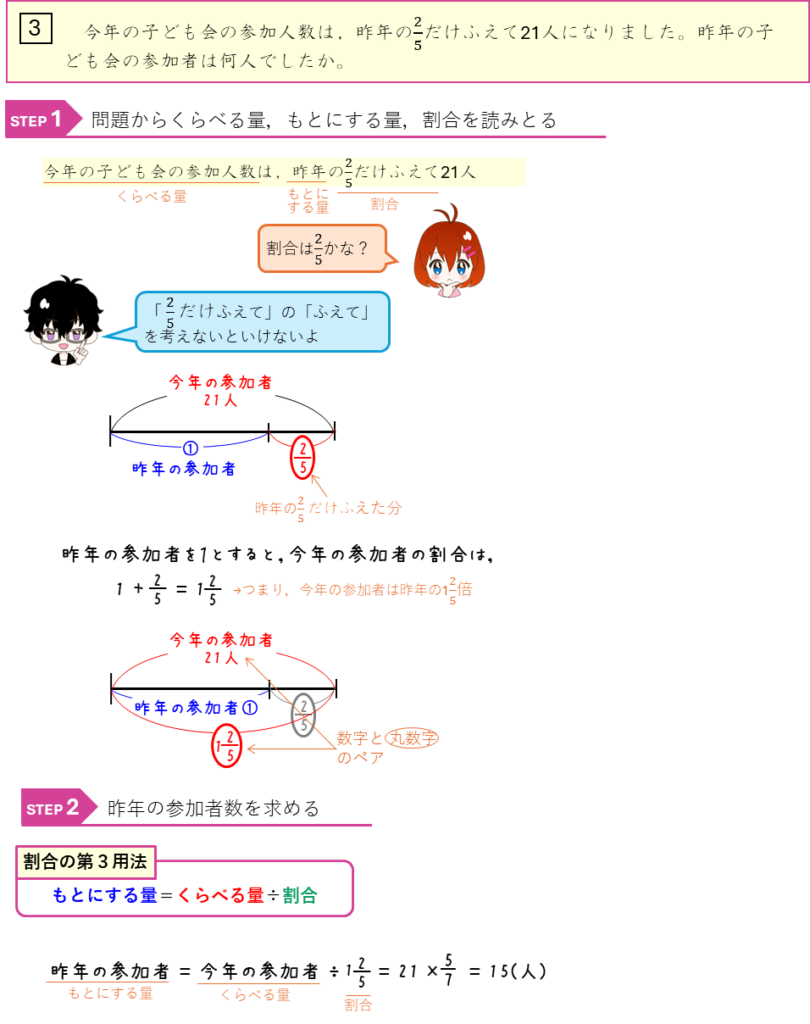
割合ー$\frac{2}{5}$だけふえる
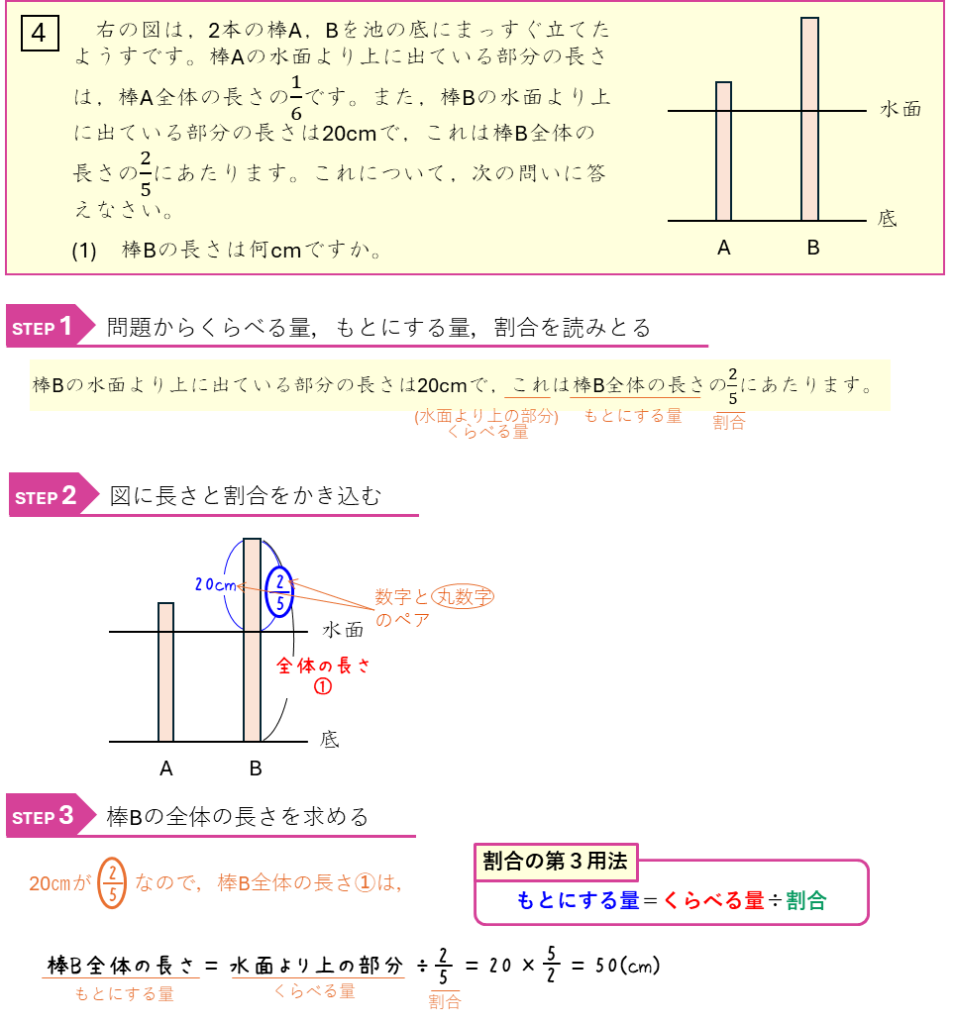
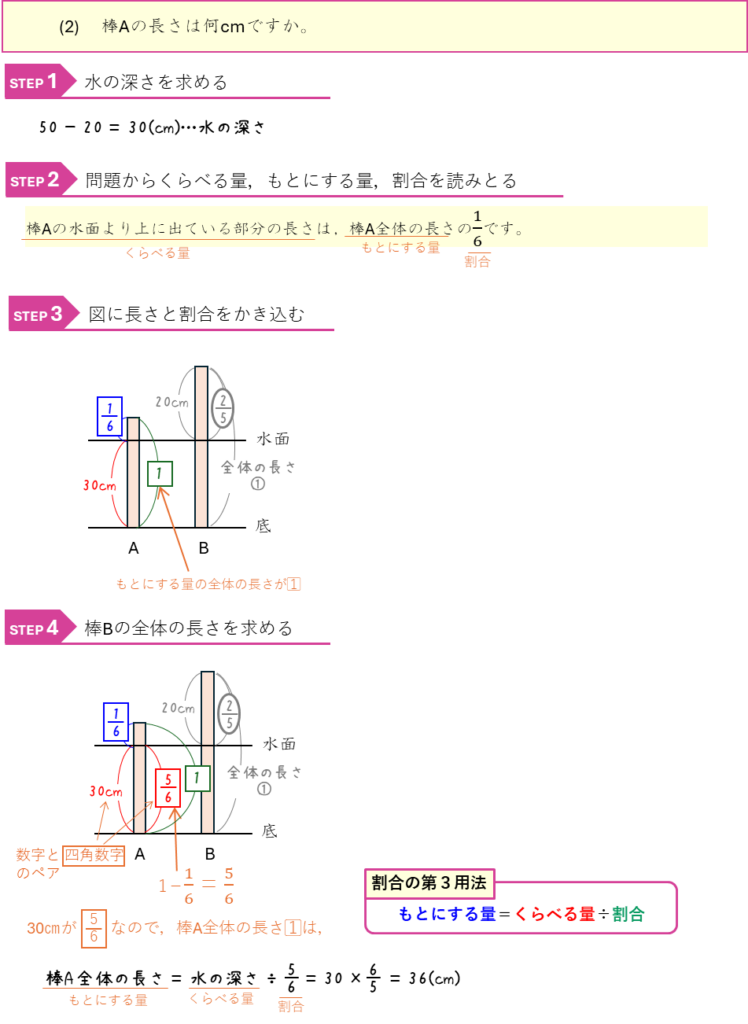
割合ー池に棒をまっすぐ立てる
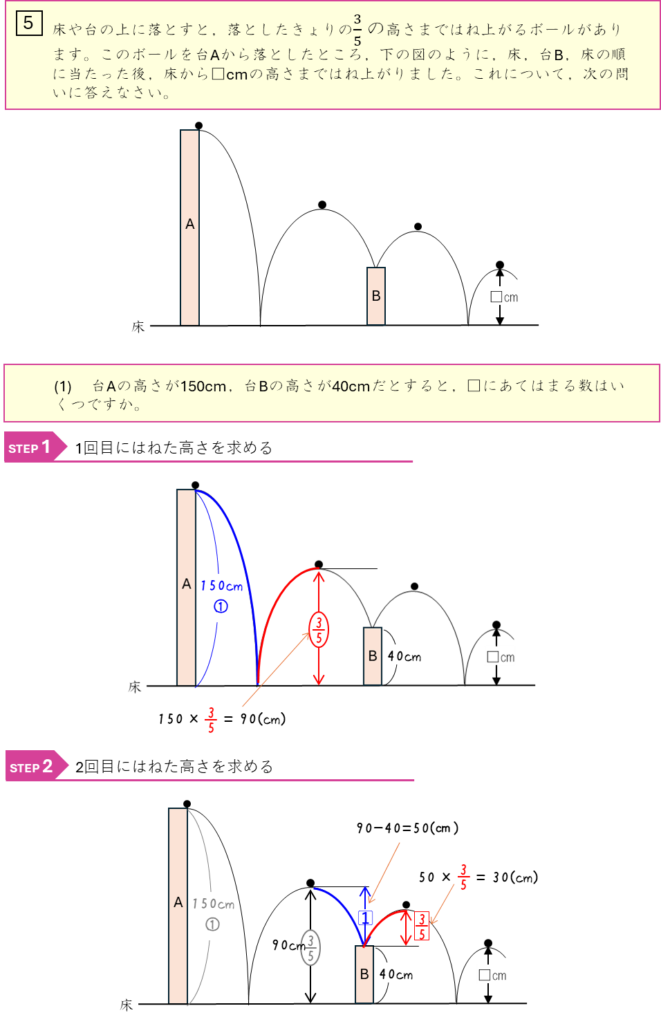
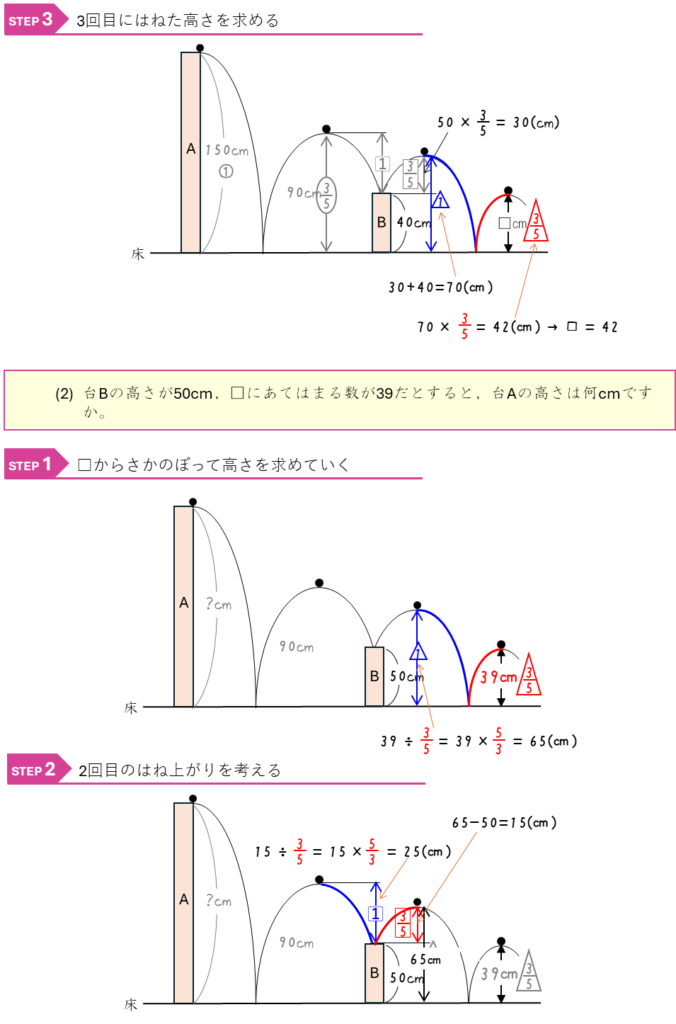
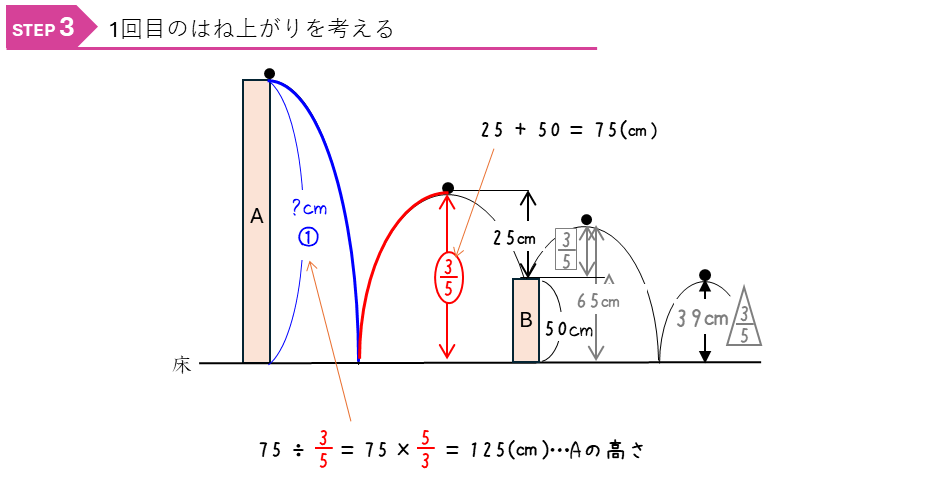
割合ーボールがはね上がる
コメント