
今回の単元では、「水量とグラフ」について学びます。立方体、直方体、角柱などの容器に水を入れていくときの水の量や水面の高さについての問題を解きます。
容器に水を入れる問題では、水面の高さの変化に注目して解く方法と、水の量に注目して解く方法があります。水の量に注目する方法は、体積を求めて解くのでイメージしやすいと思います。一方、水面の高さに注目する方法は計算が簡単になります。
水量の変化の問題は、5年生以降で応用問題を勉強します。ここでしっかりと基本を理解しておきましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
水の量(水の体積)
直方体、角柱、円柱の容器に入っている水の量(水の体積)は、
水の量(水の体積)=底面積×水の深さ
で求められます。

かさの単位(L、dL、mL)
かさの単位(L、dL、mL)と体積の単位(cm3)は、
1L=1000㎝3
1dL=100cm3
1mL=1cm3
の関係になります。牛乳の縦長のパックは1L=1000㎝3のものが多いです。日常生活の中で、L、mL、㎝3で表されるものを見つけてみてください。

水量の変化とグラフ
水量の変化は、
たて軸: 水面の高さ(㎝)
横軸: 時間(分)
のグラフで表されます。

練習問題
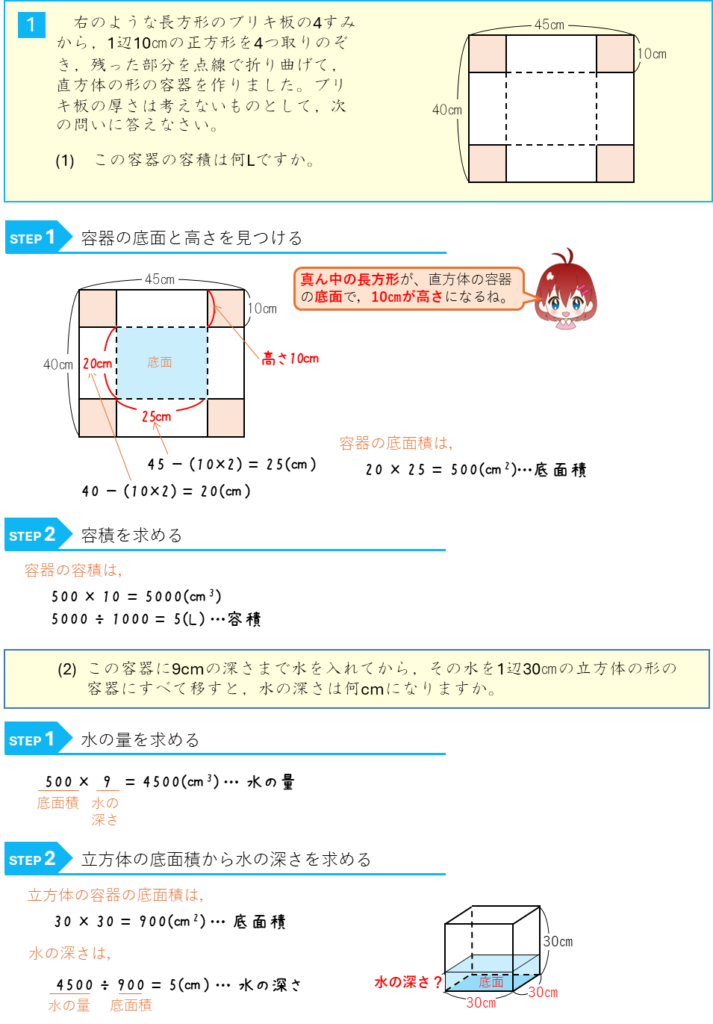
水量と水の深さー展開図から容積を求める
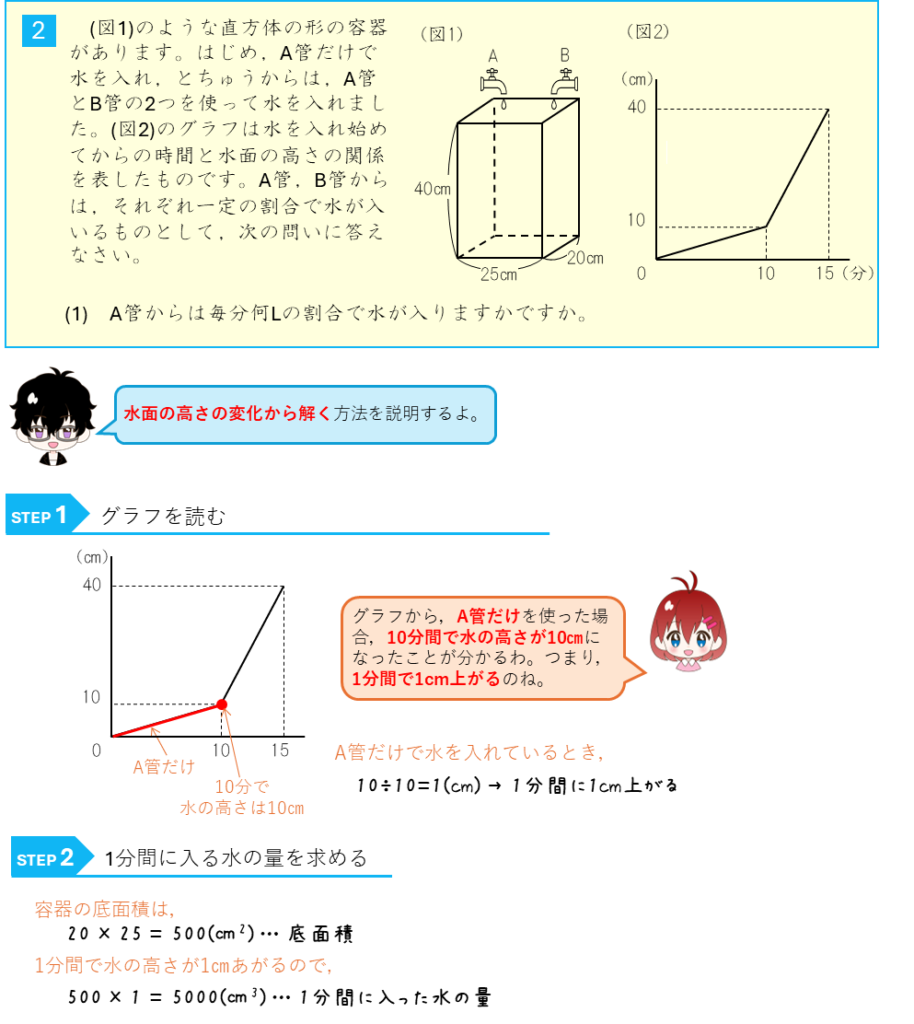
水面の高さの変化とグラフー2つの給水管から水を入れる
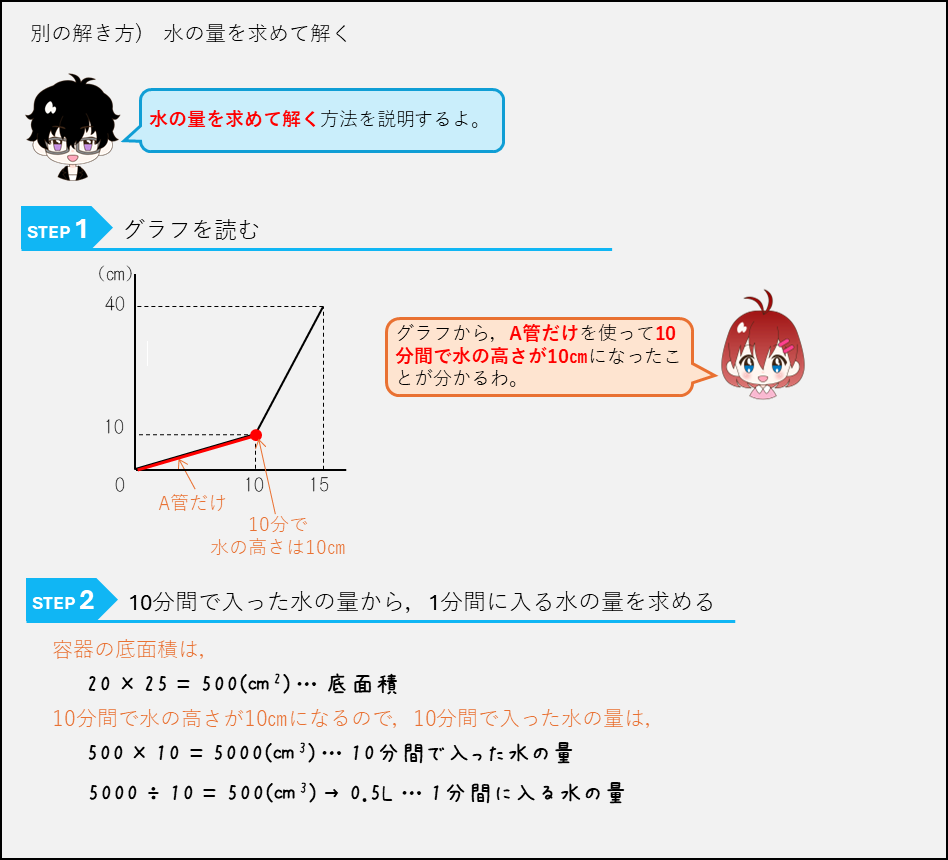
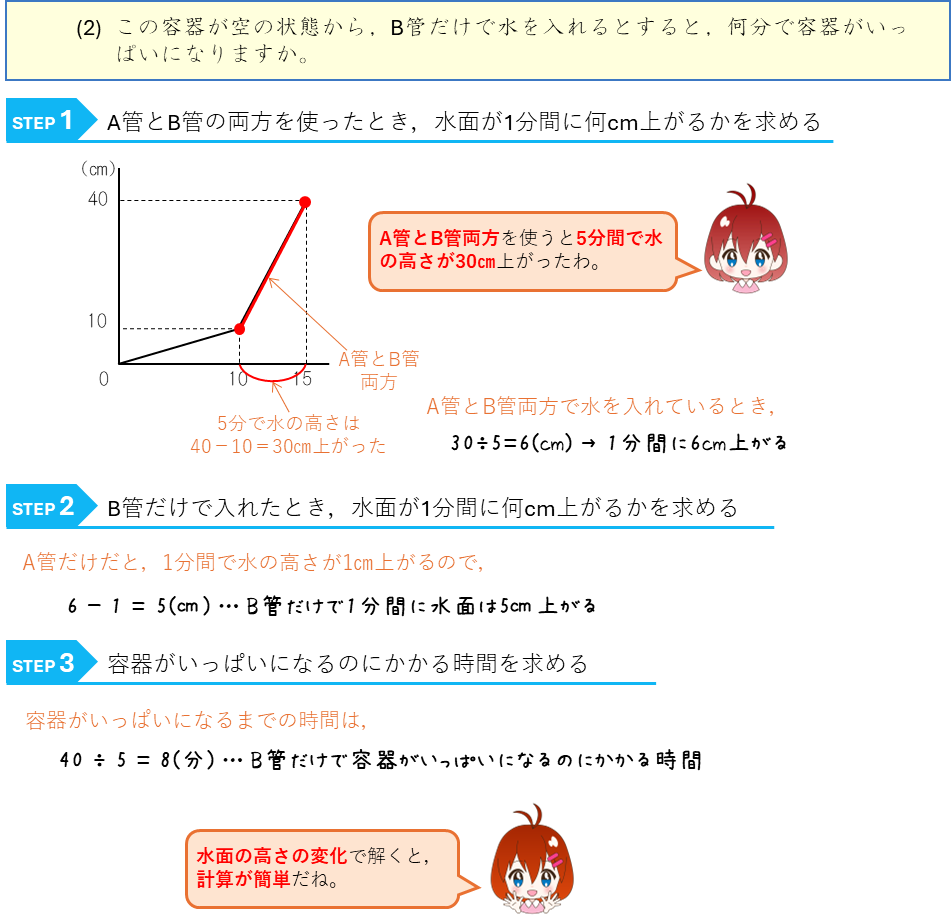

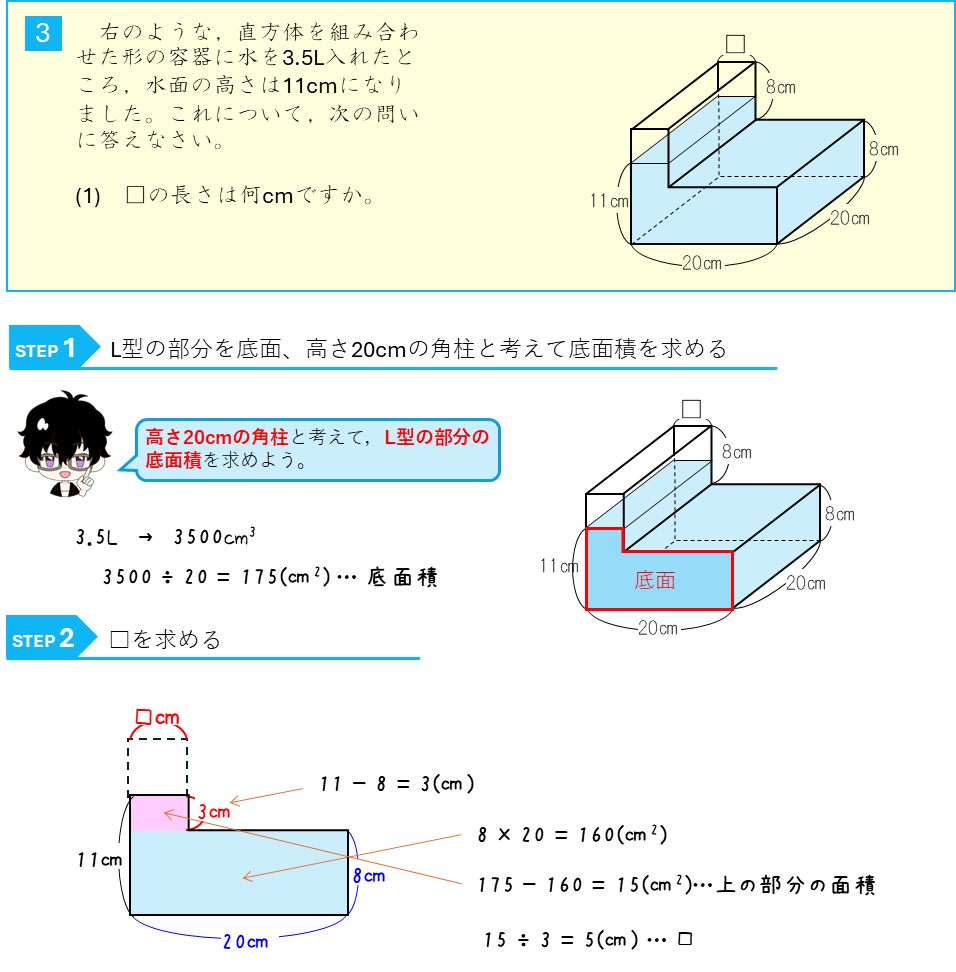
水量と水の深さー直方体を組み合わせた容器に水を入れる


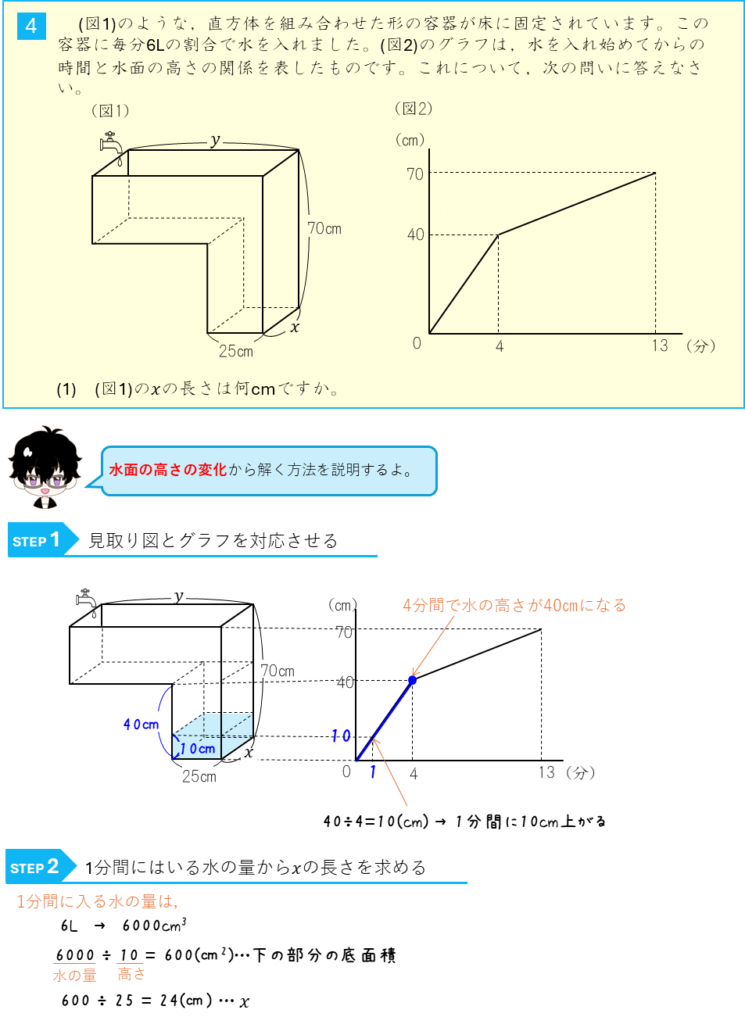
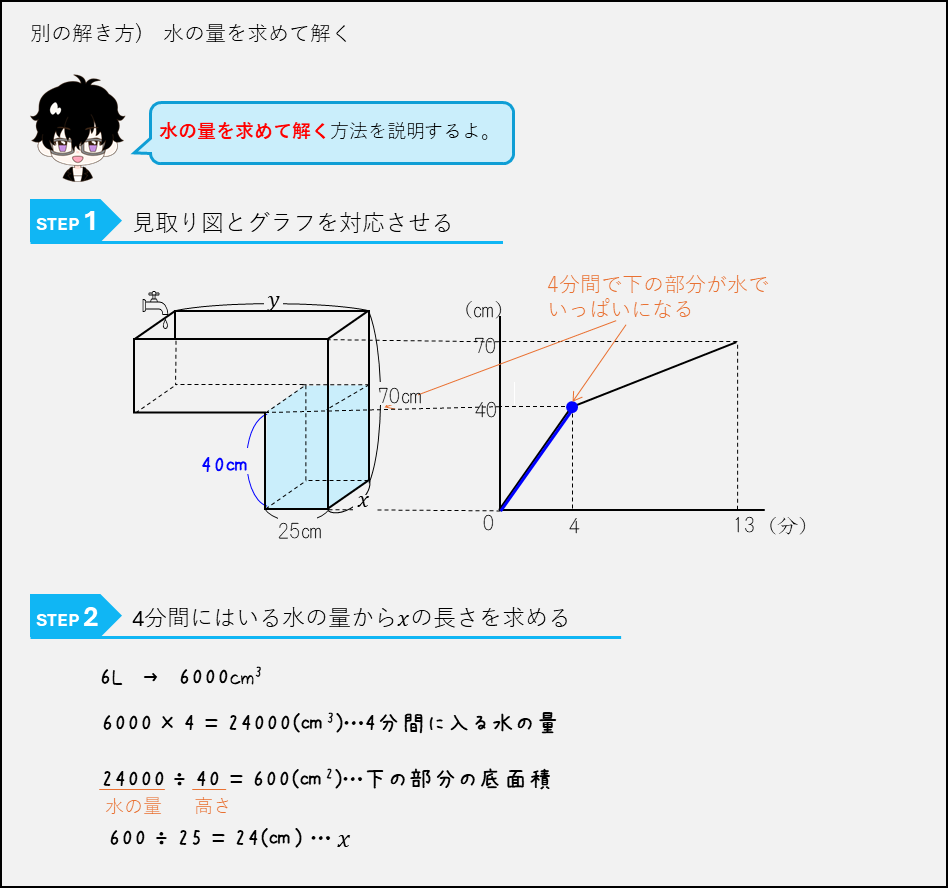
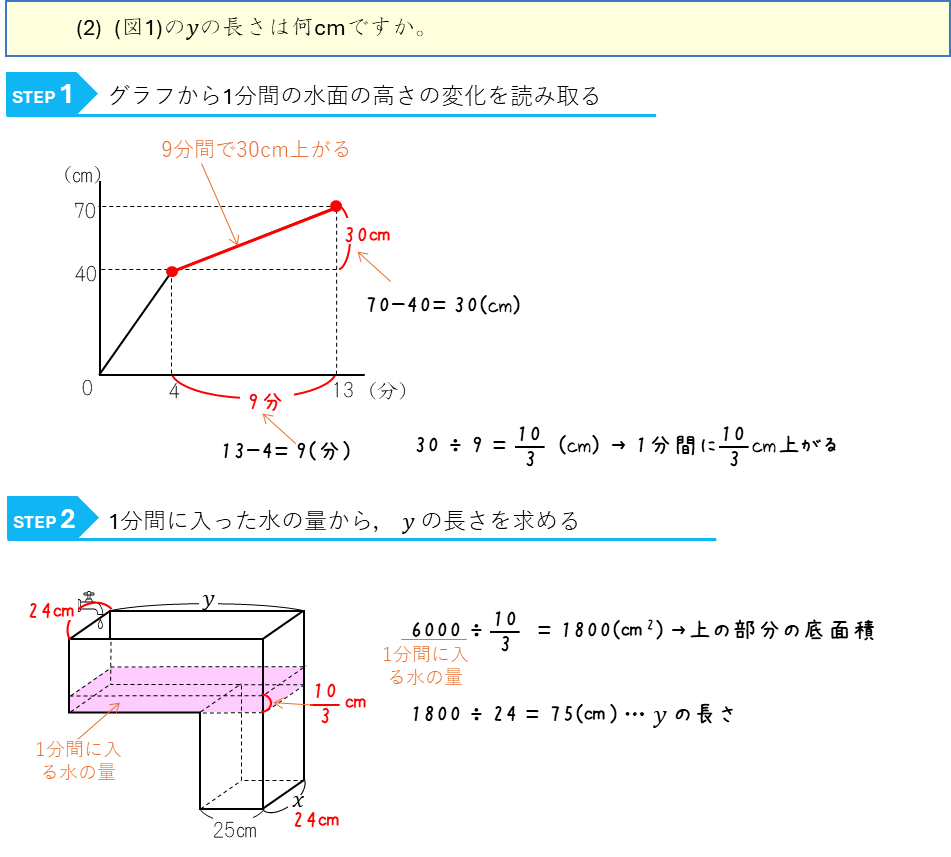
水面の高さの変化とグラフー直方体を組み合わせた容器に水を入れる


コメント