
今回の単元では、立体図形の「角すいと円すい」について学びます。角すいと円すいの体積は、
体積=底面積×高さ÷3
という公式で求められます。問題から、底面とそれに垂直な高さを見つけ出せれば、この公式から体積を求めることができます。÷3を忘れないようにしましょう。
円すいの側面については、
底面の円周の長さと、側面の弧の長さが等しい
という関係があります。これから側面の公式を導き出すことができます。すばやく問題を解くために、側面の公式を覚えましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
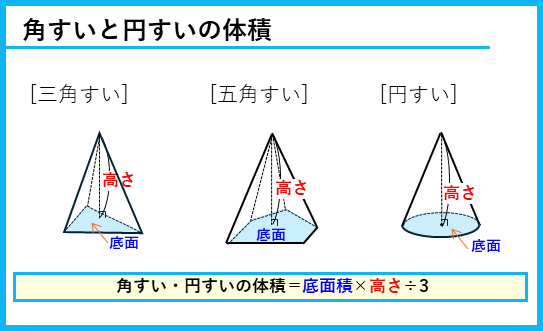
角すいと円すいの体積
角すいと円すいの体積は、
体積=底面積×高さ÷3
で求められます。同じ底面積の角柱や円柱の体積の$\frac{1}{3}$になります。計算で÷3(×$\frac{1}{3}$)を忘れないようにしましょう。
円すいの側面の公式
円すいの展開図を見ると、底面の円と側面のおうぎ形からできていることが分かります。このとき、底面の円周の長さと側面のおうぎ形の弧の長さが等しくなります。
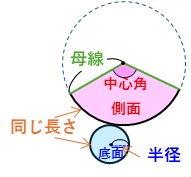
これがとても大切な性質で、ここから、円すい側面のおうぎ形の中心角や、側面の面積を求めることができます。これを整理すると、次のような公式になります。
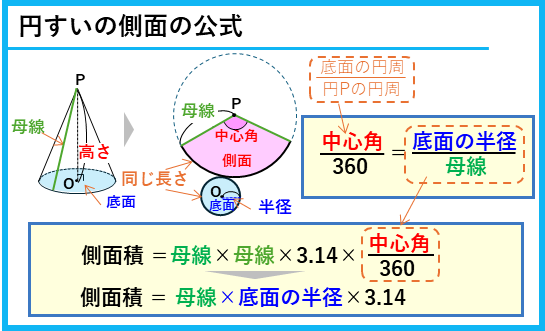
公式を使うと計算が簡単になるので、覚えて活用しましょう。もしも、公式を忘れてしまった場合には、
底面の円周の長さ=側面のおうぎ形の弧の長さ
の性質から解くことができますので、この原理はしっかり覚えておきましょう。
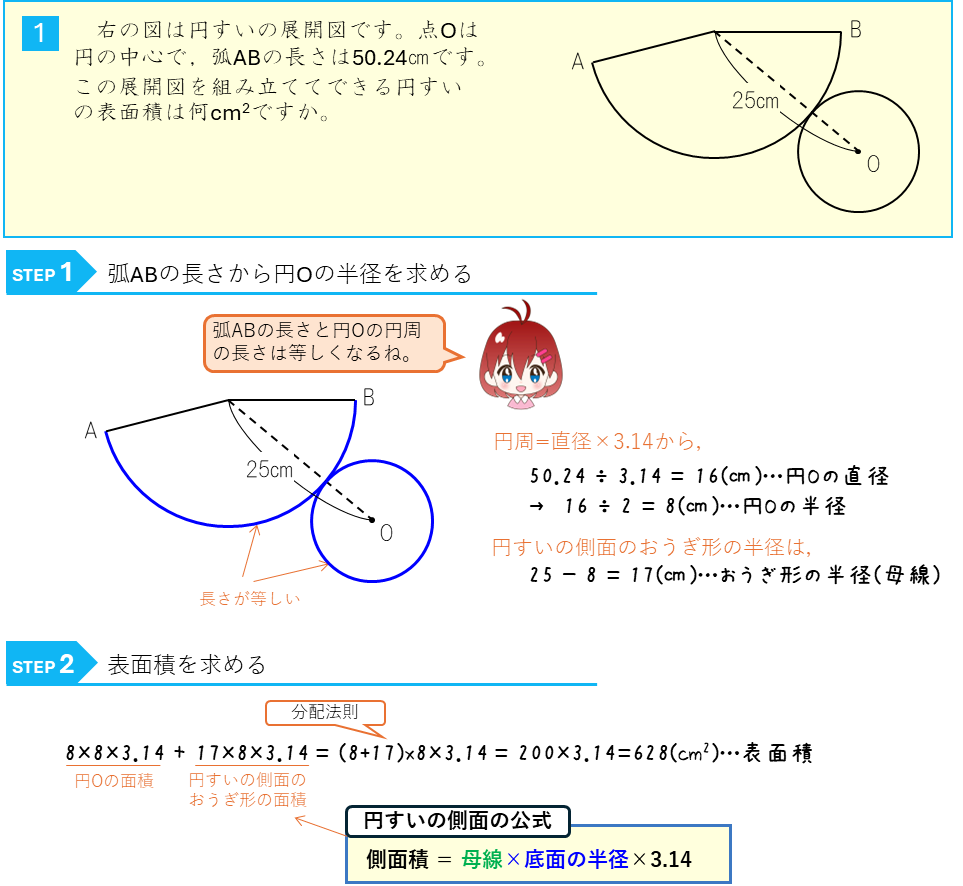
練習問題
円すいの表面積ー弧の長さから求める
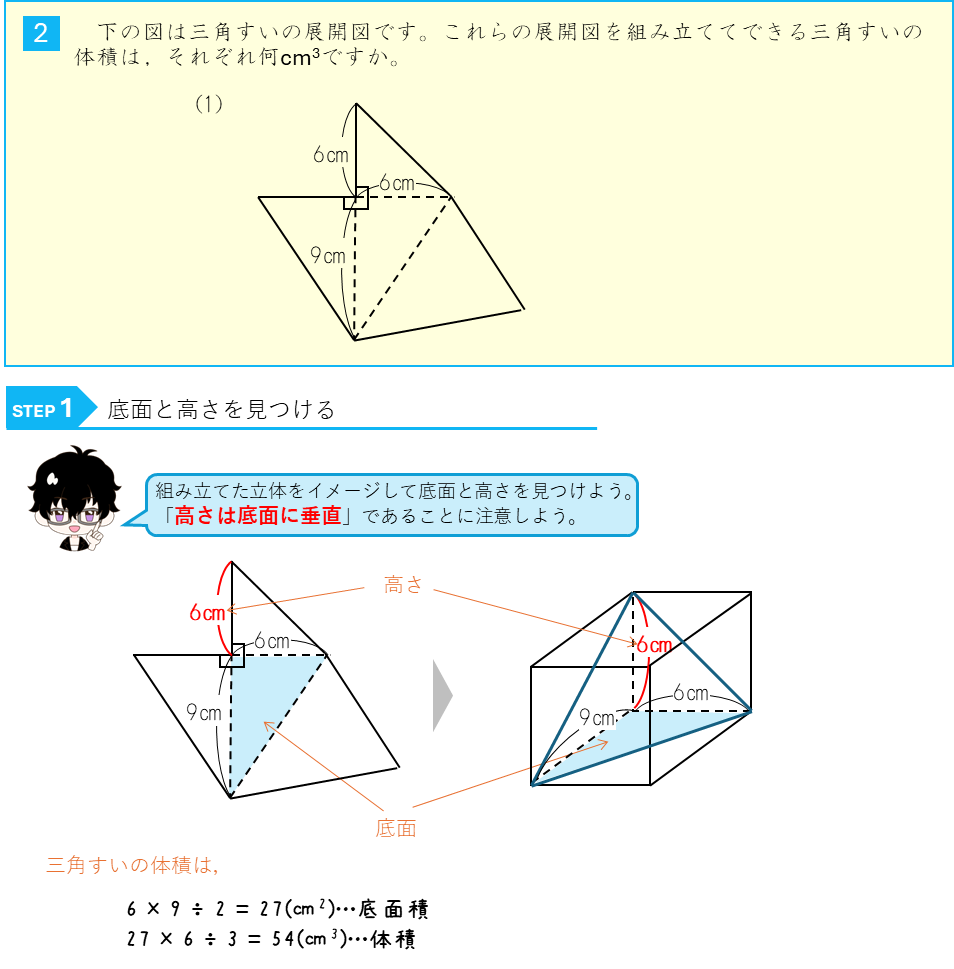
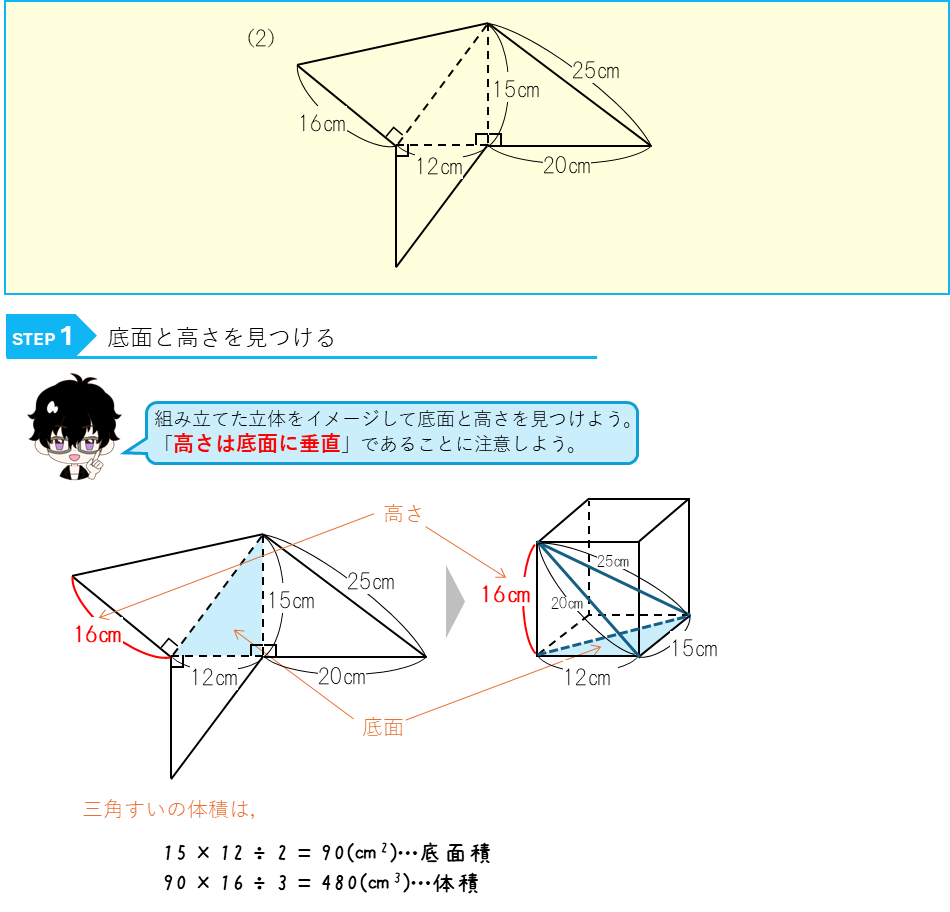
三角すいの体積ー展開図から求める
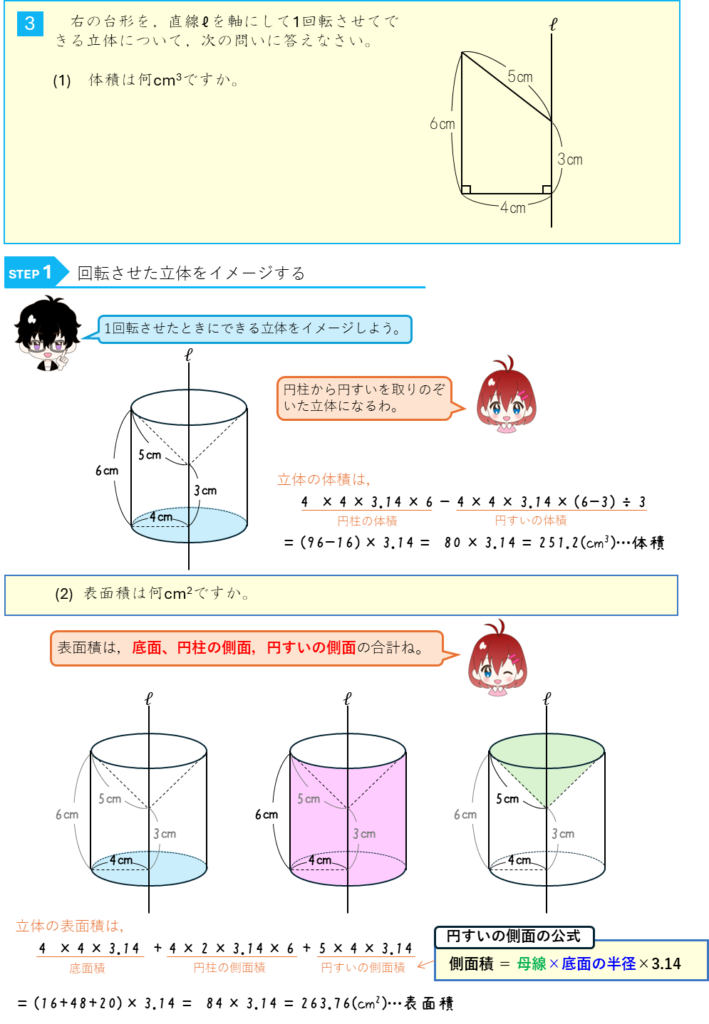
回転体ー円柱から円すいを取りのぞいた立体
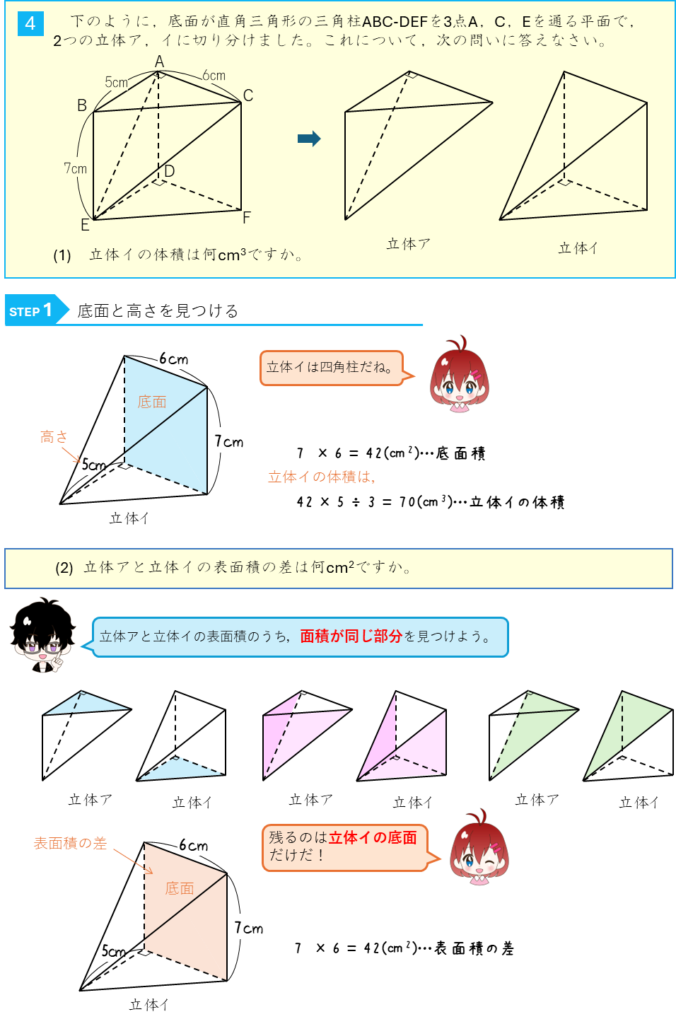
三角柱を切り分ける
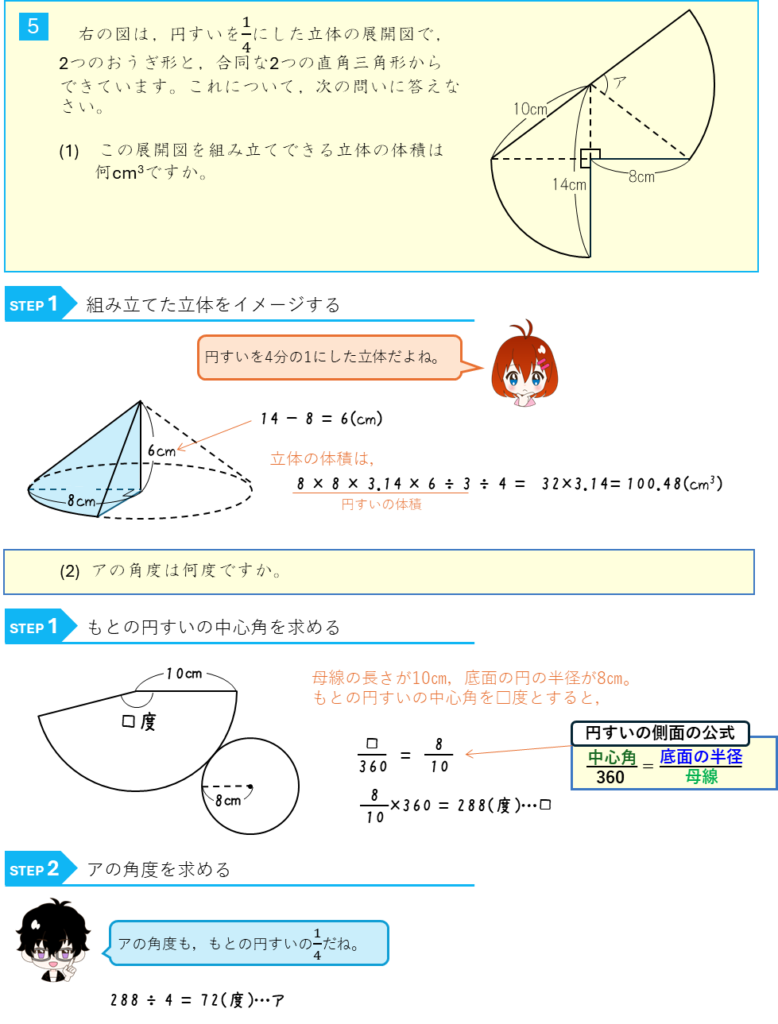
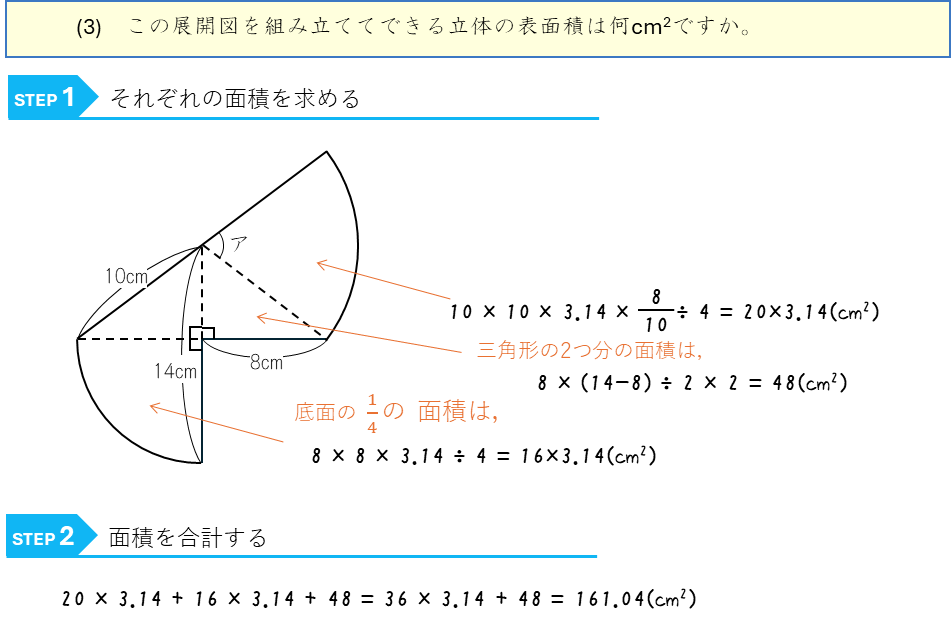
円すいを4分の1にした立体の展開図

コメント