
図形の単元が続いていましたが、今回は、「消去算」という式で問題を解いていく内容になります。
問題文から複数の式を立てて、それらの差から解く「加減法」や一方の数量をもう一方の数量におきかる「代入法」を使って解いていきます。これらの解法を使えば、同じように解いていけるので、しっかり理解して身に付けましょう。
(四谷大塚 予習シリーズ算数 四年下の解説です。テキストは四谷大塚から購入してください。)
解説
消去法の式の基本
消去法の例題の1部です。


のように絵をかくとイメージがわきますが、問題を解くたびに、このような絵をかいていたら大変ですね。そこで、

のように、式を使って表現します。ここで、問題から右の式を作って、その式から左の絵をイメージできることが大切です。
また、消去法の式では次のように、たし算、ひき算、かけ算、わり算ができます。
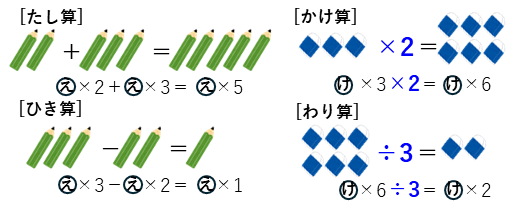
絵と式の対応を確認してください。

のようにイメージできていれば、普通のたし算、ひき算、かけ算、わり算と同じように計算すればよいことが分かると思います。
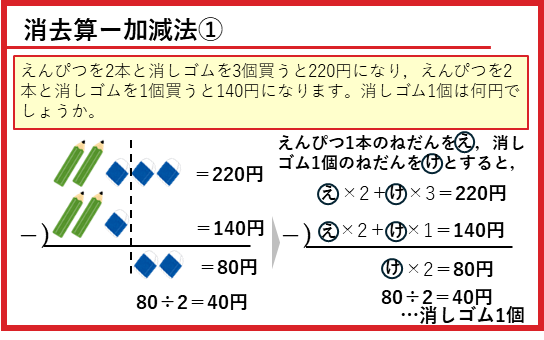
消去算ー加減法

を解いていきます。まず、絵を描いて考えてみます。

2つの差を考えると、えんぴつと消しゴム1個が消えて消しゴム2個分が80円だと分かります。したがって、消しゴム1個のねだんは40円です。これを式で解いていくと次のようになります。

この式の計算で、上の絵と同じことが理解できればOKです。このように、消去算を式の差をとって、一方の量を消して解く方法を「加減法」と言います。
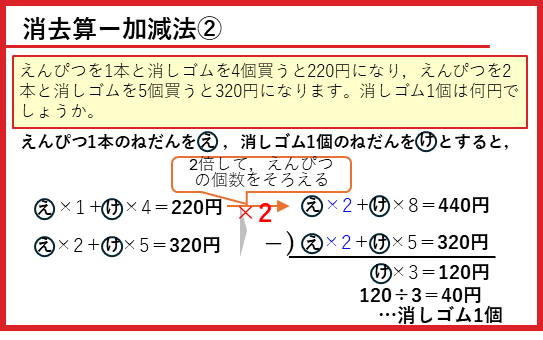
次の例題です。

式をたてると、

になります。そのまま差をとってもうまくいきません。この場合は、式を何倍かしてえんぴつの本数をそろえます(あるいは、消しゴムの個数をそろえる)。上の式を2倍してえんぴつの本数を2本にそろえてみます。その後で差をとることでえんぴつが消え、消しゴムだけの式を作ることができます。

式を2倍するとき、えんぴつの本数だけでなくて、消しゴムの個数、合計の代金もしっかり2倍することを忘れないようにしましょう(あたり前なのですが、うっかり忘れることがよくあるので要注意です)。
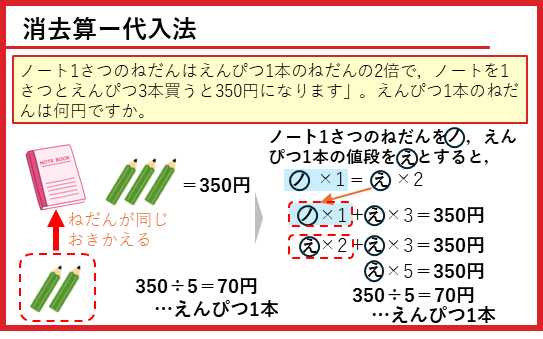
消去算ー代入法

この問題では、
ノート1冊のねだん=えんぴつ2本分のねだん
が分かっています。そこでノートをえんぴつにおきかえることで、解くことができます。この方法を「代入法」と呼びます。

式をかいて解いていくと、

となります。絵と同じようにイメージを持って解くことができたでしょうか?
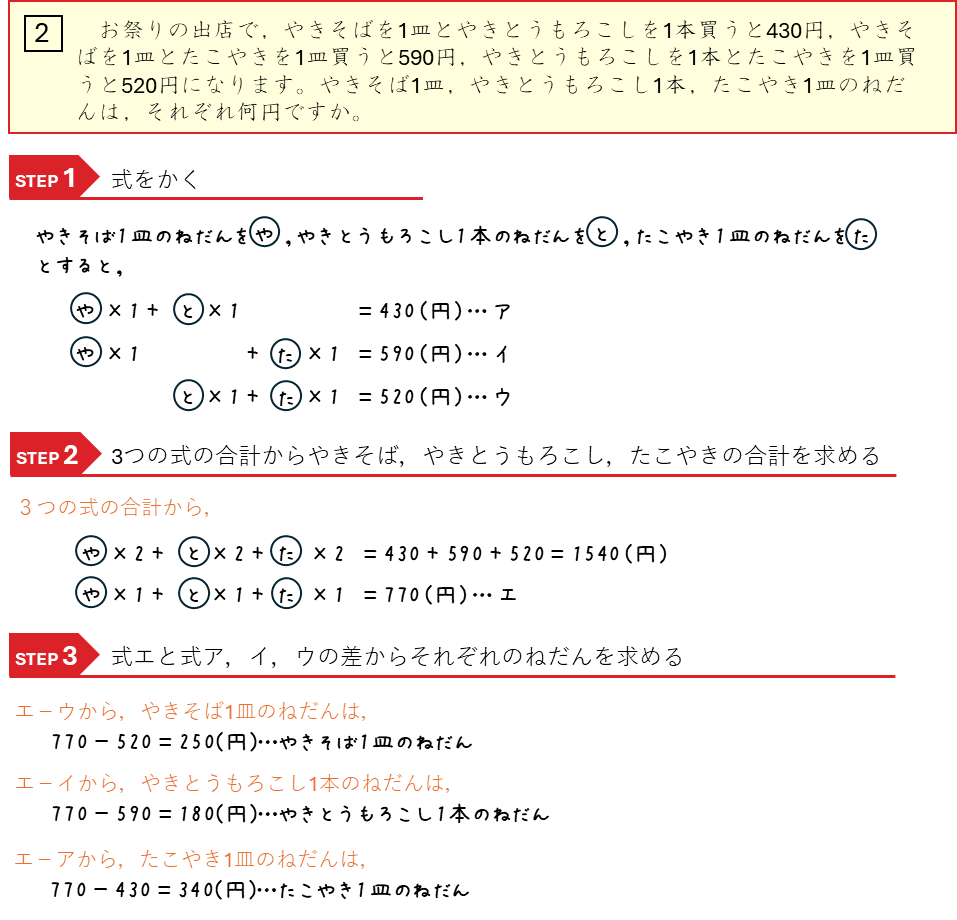
3量以上の消去算
3量以上の消去算では、それぞれ1個ずつのセットの合計のねだんを求めてから、個々のねだんを求めていきます。

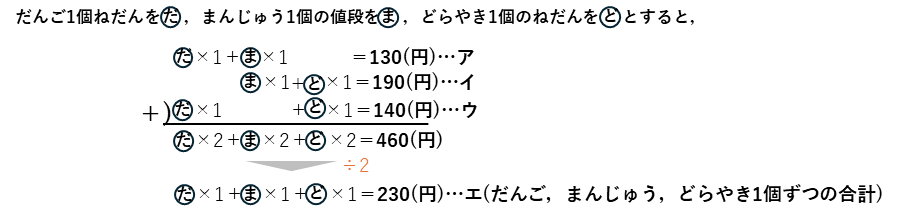
エとの差で、だんご、まんじゅう、どらやき1個のねだんを求めます。
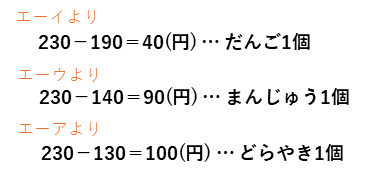
消去算まとめ
以上の内容を、復習用にカードにまとめます。
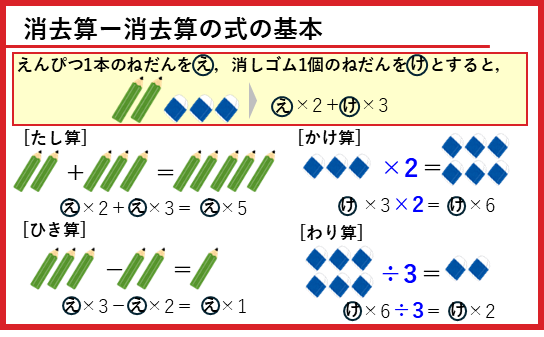

練習問題
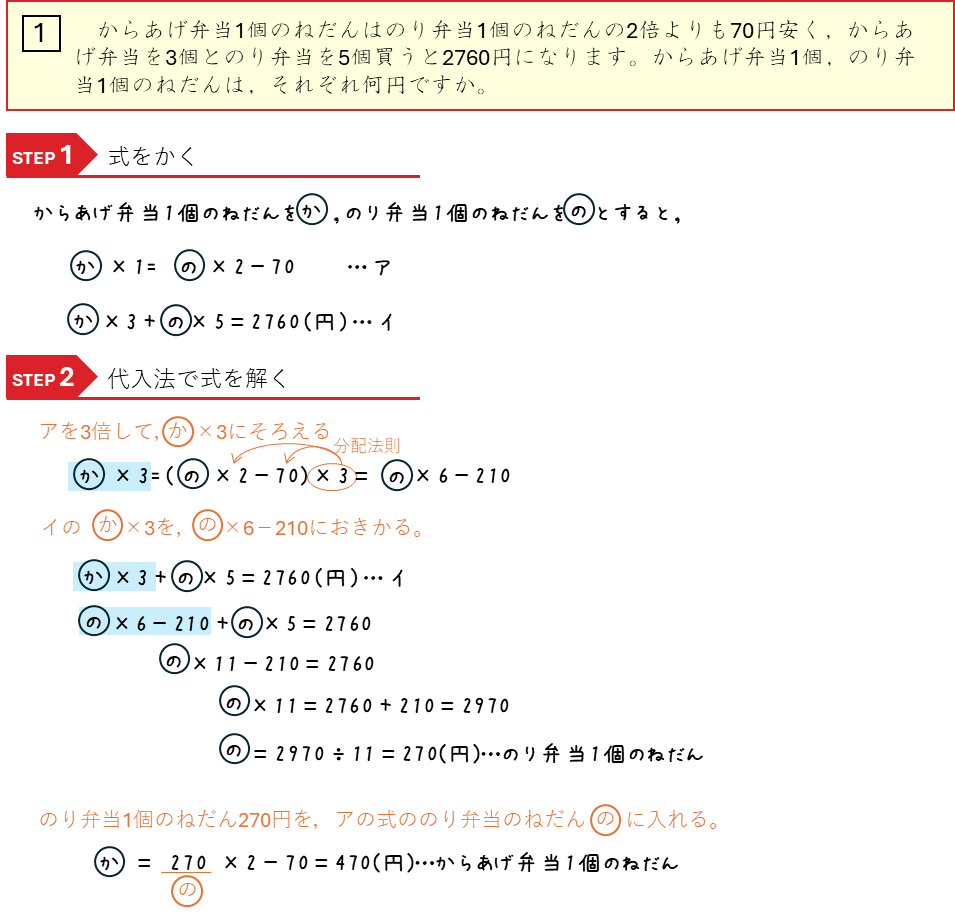
消去算ー代入法(はんぱあり)
からあげ弁当のねだんが、のり弁当のきっちり2倍ではなくて、2倍より70円安いというはんぱがあります。分配法則を使って解きましょう。
消去算ー3量の消去算
消去算ー180人の生徒の合計

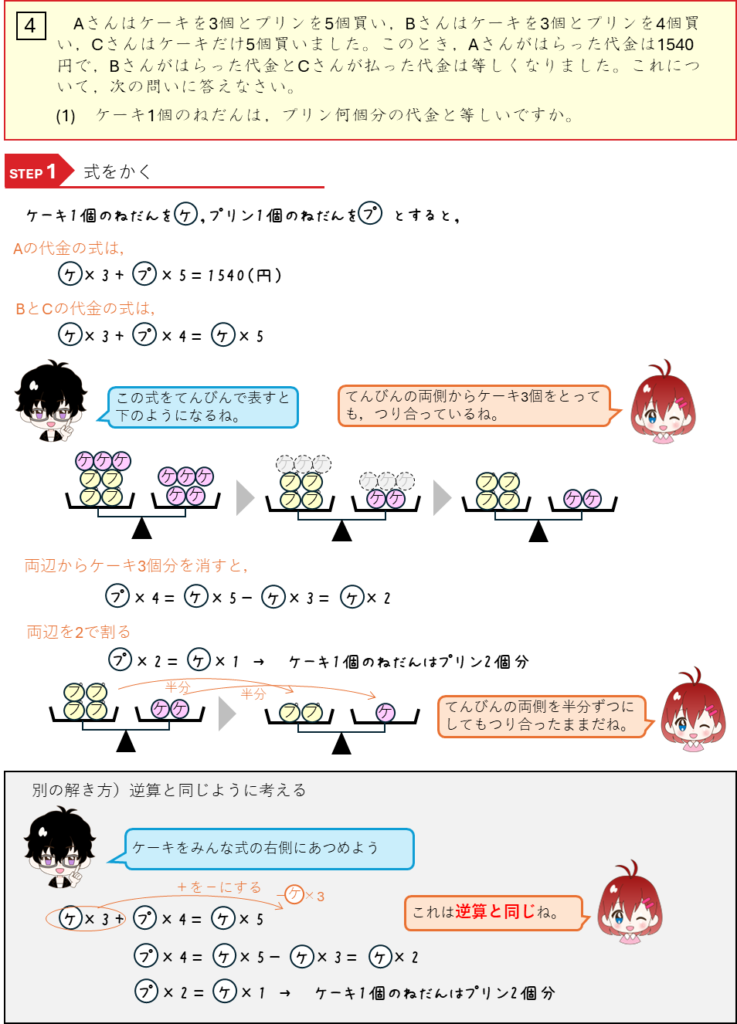
消去算ーケーキ3個とプリン4個の代金とケーキ5個の代金が等しい

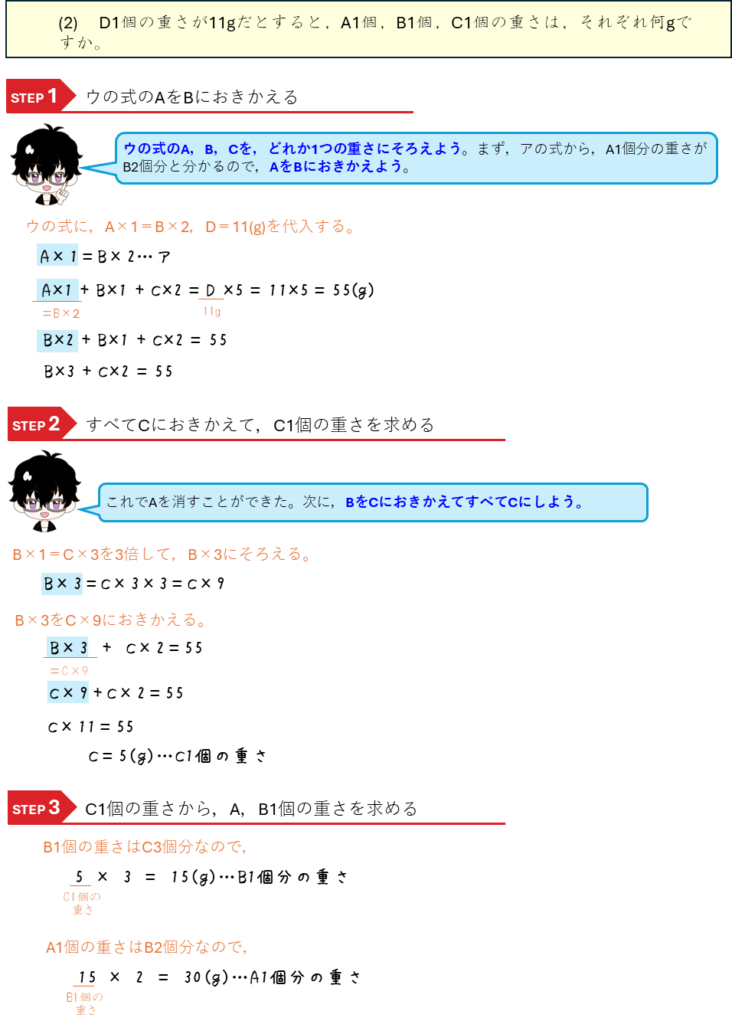
消去算ー3量以上の消去算


コメント