この単元では、立方体と直方体について勉強していきます。立方体の展開図やさいころについての問題を、立方体の性質を使って解いていきます。立体図形についてはじめて取り組みで、難易度の高い単元になっていると思います。特に、立体図形をイメージするのが難しいので、わかりやすい図にかきかえて解いていく方法を理解していきましょう。(四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
解説

今回は、立方体と直方体について勉強するよ。立体図形としてはじめてだね。立体図形は、イメージするのがとても難しいのと、問題の難易度も高いのでかなり苦戦しそう。展開図についての問題が多いので、展開図の性質をしっかり使えるようにしよう。
これからできるだけ、ていねいに説明していくので、いっしょに勉強していこう。
立方体と直方体
まずは、立方体と直方体の基本だ。
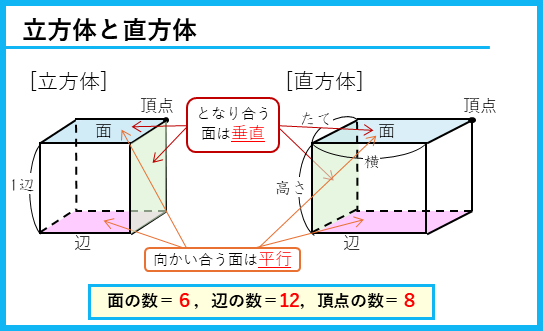
立方体は正方形に、直方体は長方形に囲まれた立体だ。ふだんの生活でも見なれた立体だよね。立方体、直方体の、
- 向かい合う面は平行
- となり合う面は垂直
という性質がある。また、
- 面の数は6
- 辺の数は12
- 頂点の数は8
になる。図形からこれらの数はわかるよね。
立方体の展開図
立体の辺を切り開いて平面にした図を「展開図」というよ。立方体の展開図については、次のような性質がある。
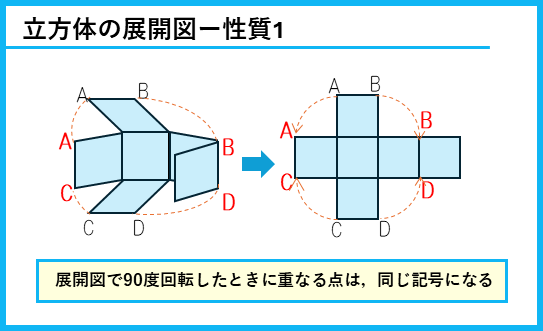
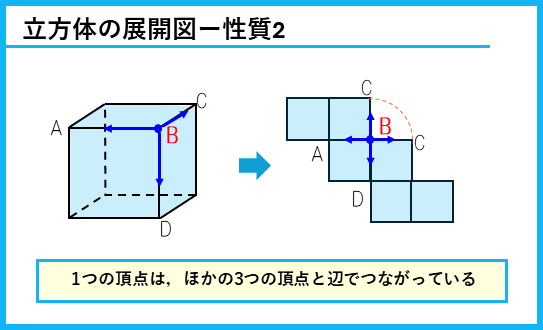
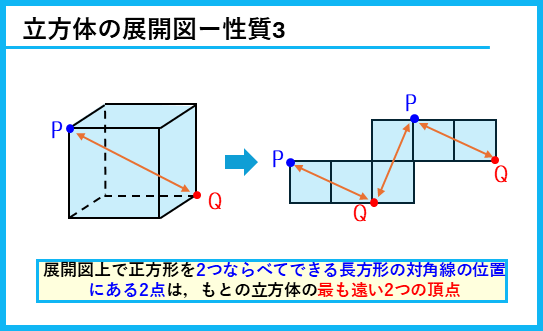
これらの性質は、問題を解くのに使っていくのでしっかり覚えておこう。
立方体の展開図の種類・・・11種類
展開図が立方体に組み立てられるかを問う問題がよく出題されるよ。立方体の展開図は11種類ある(左右対称、回転したとき同じになるものをのぞく)。
それぞれの行の正方形の数で分けると、1-4-1型、1-3-2型、2-2-2型、3-3型の4種類になる。
●1-4-1型・・・6種類
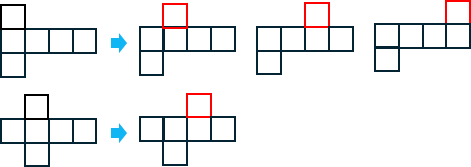
左のを基本形に上の正方形の位置がことなるものがあると考えると覚えやすいよ。
●1-3-2型・・・3種
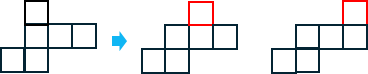
左の基本形に上の正方形の位置を変えたものをふくめて3種類ある。
●2-2-2型・・・1種

●3-3型

ほかに、2-2-2型、3-3型が、それぞれ1種類ずつある。3-3型だけが2段になるね。
さいころは、向かい合う目の和が必ず7になることは知っているよね。これらの展開図で向かい合う面がどの組になるかも整理しておこう。
向かい合う面の判定
向かい合う面のパターンは以下の4つがある。
特に、左の2つのパターンはよく覚えておこう。では、11種の展開図で向かい合う面はどうなるかな?

一度、自分でもぬり分けてみるといいよ。ぜひやってみて。
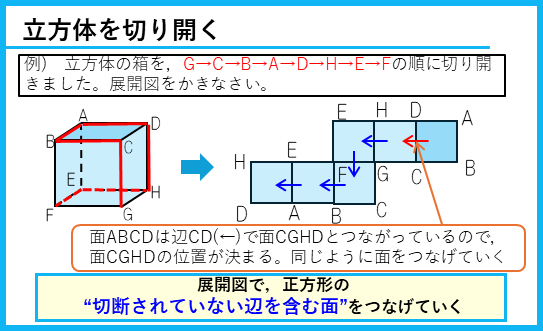
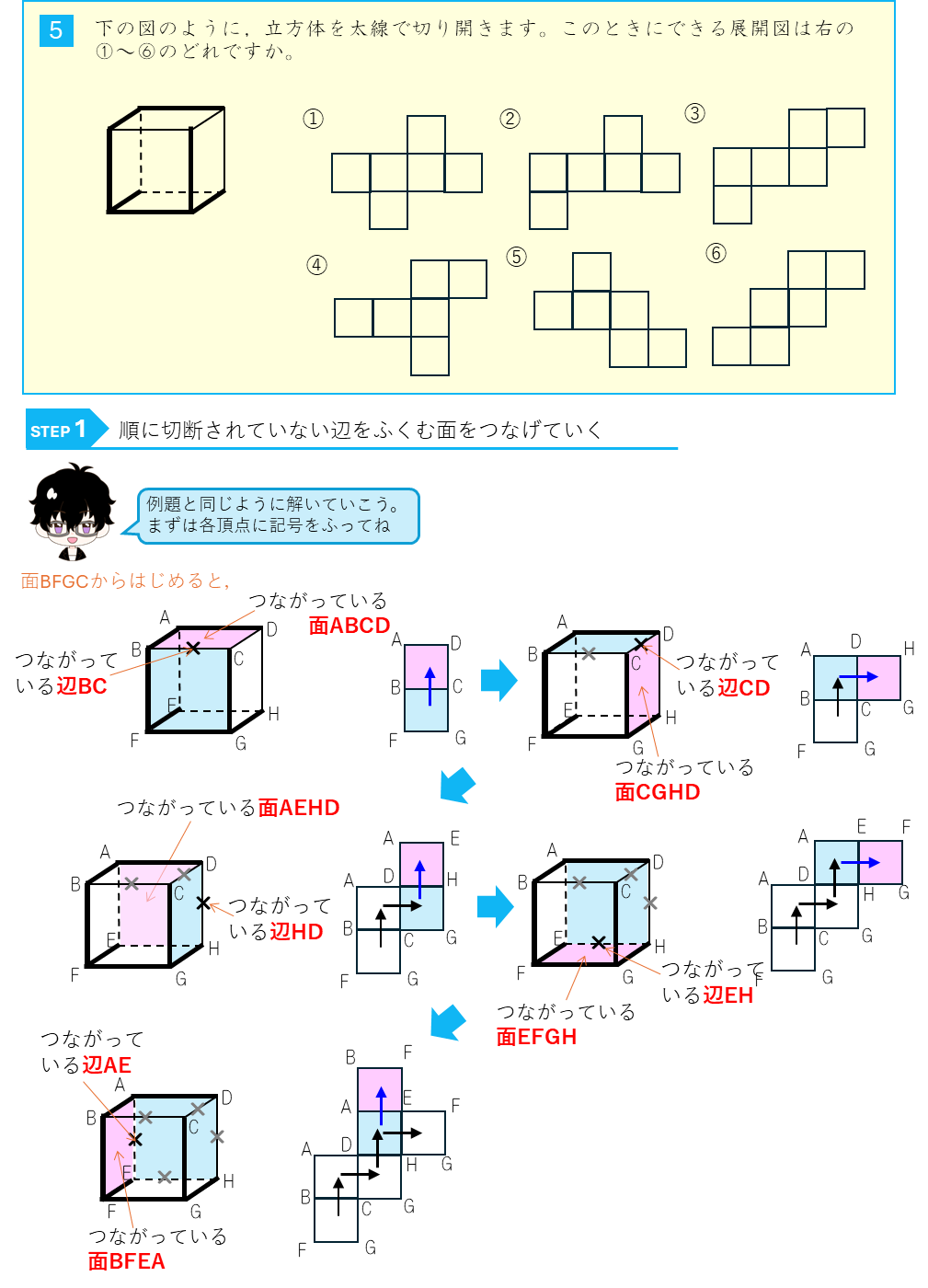
立方体を切り開く
例題4はかなり難しい問題だ。解き方を詳しく説明していくよ。
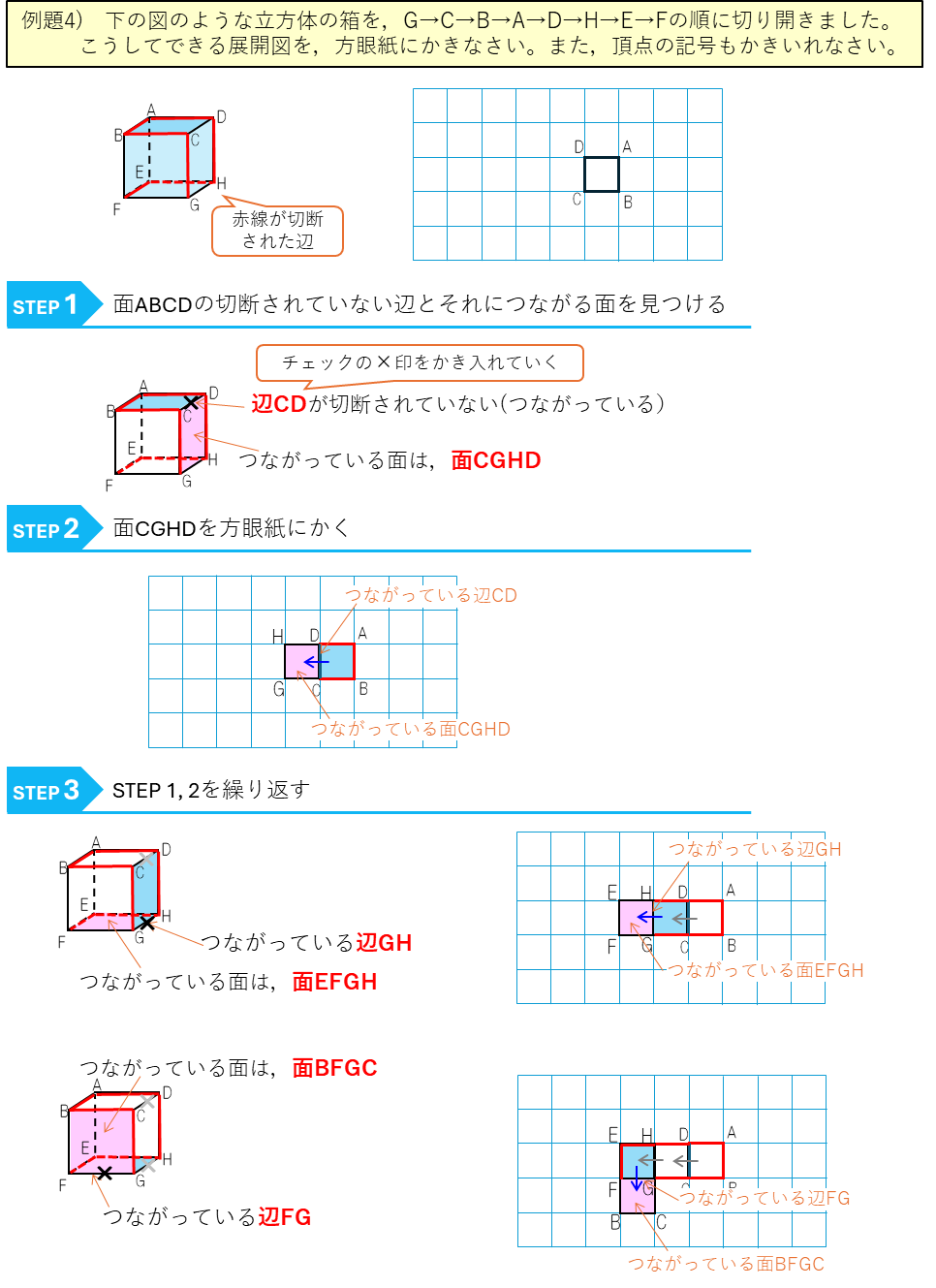
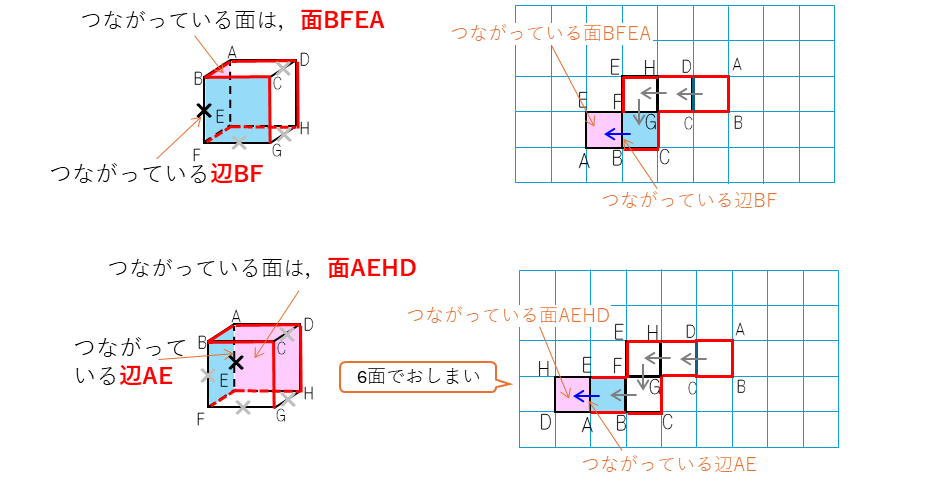
ちょっと大変だけど、このように一面ずつ考えていけばいいんだ。解法としてカードにしておくよ。
練習問題
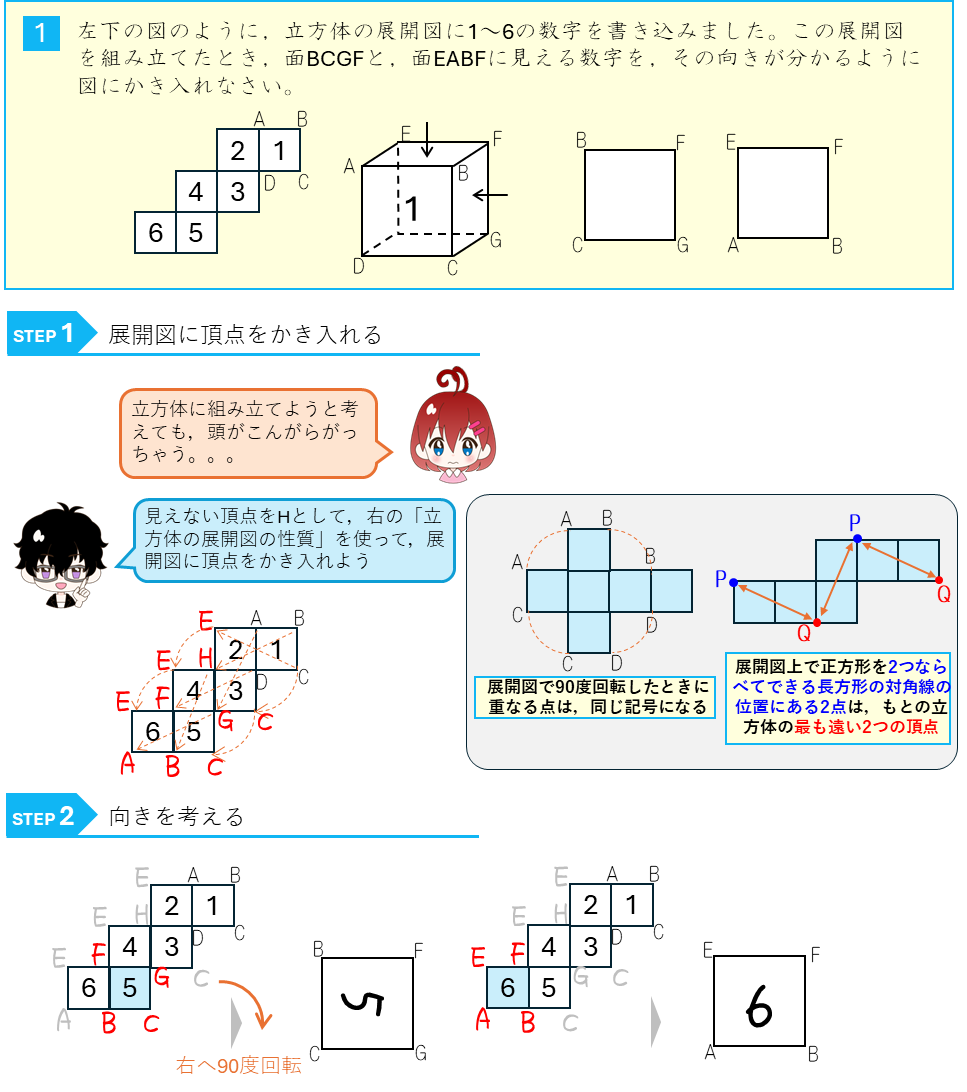
立方体の展開図ー対応する面
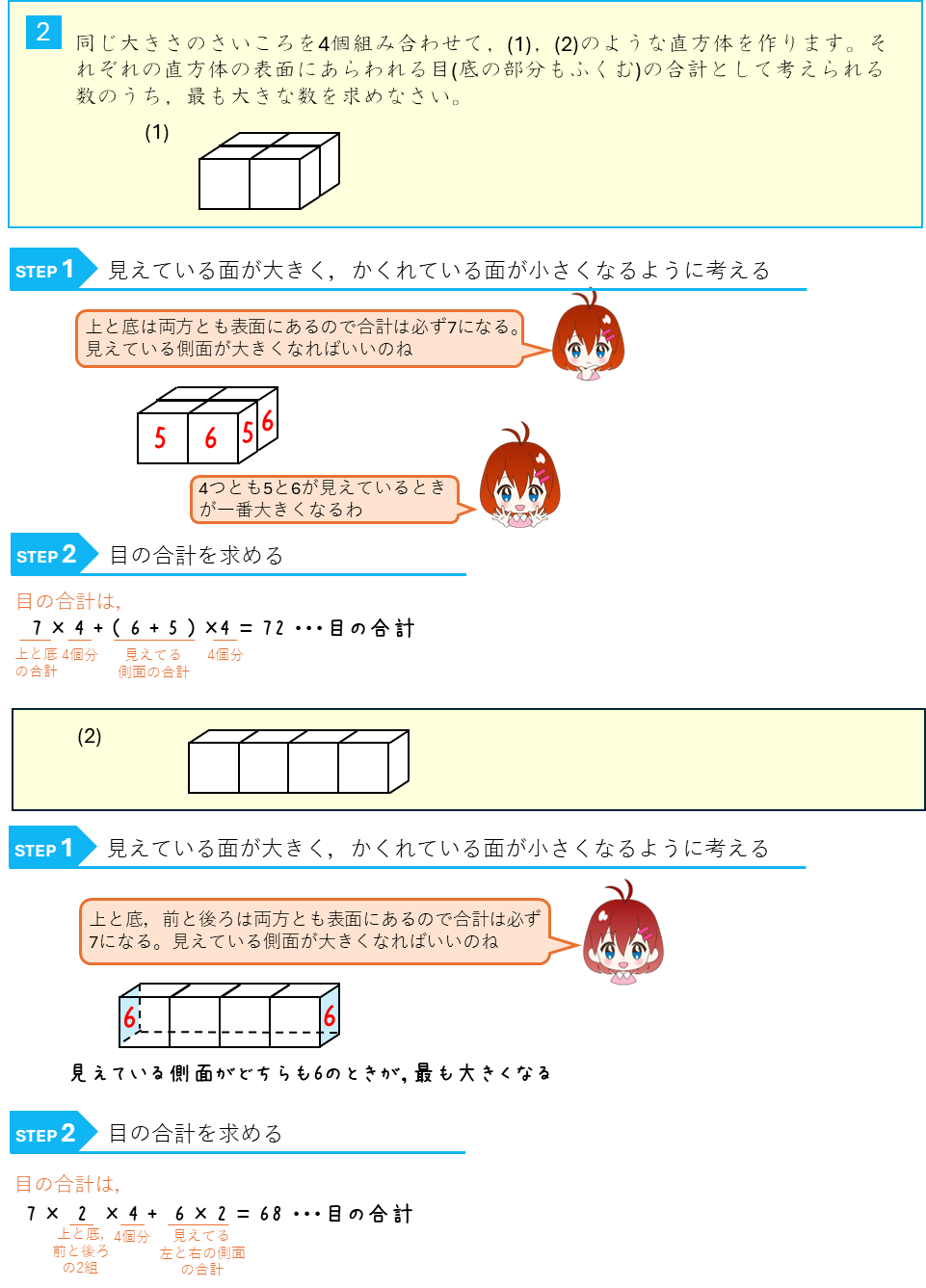
さいころの目の合計
立方体の展開図
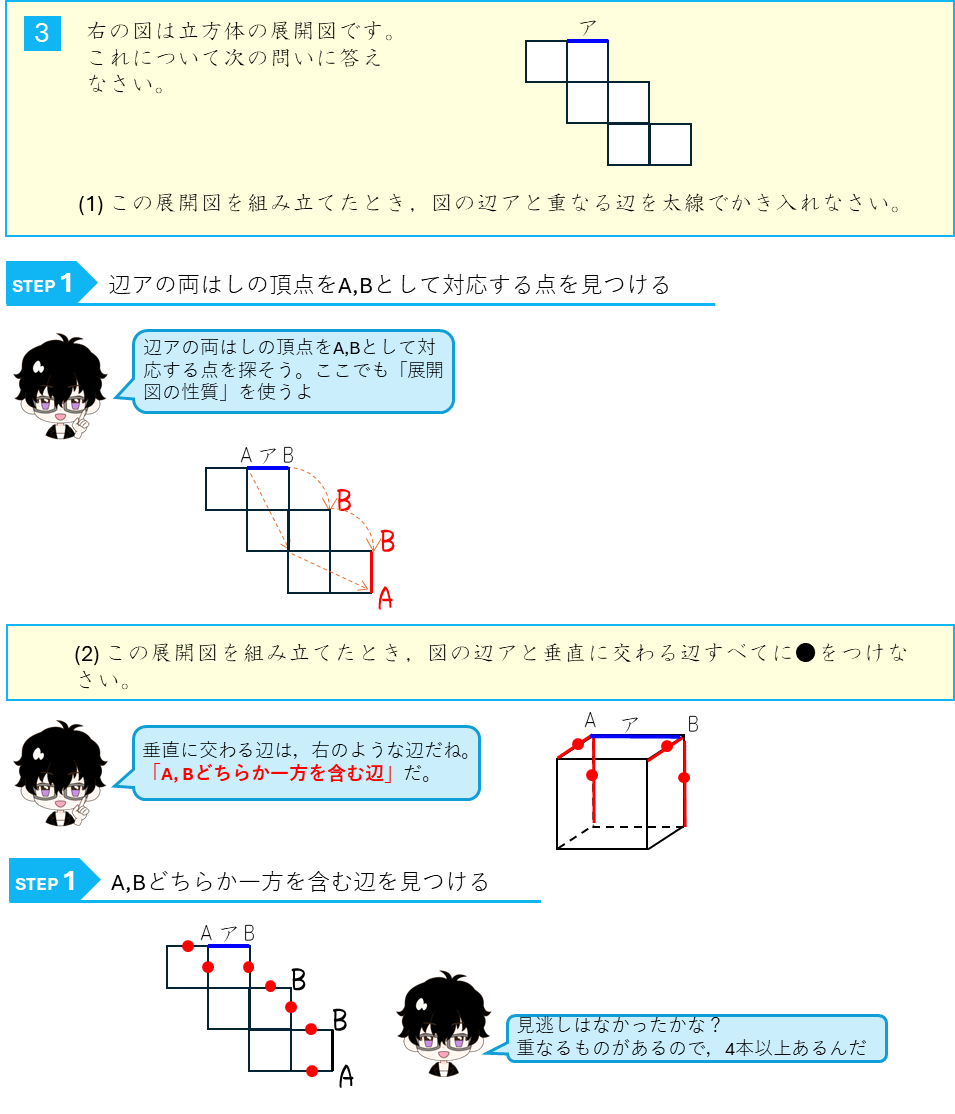
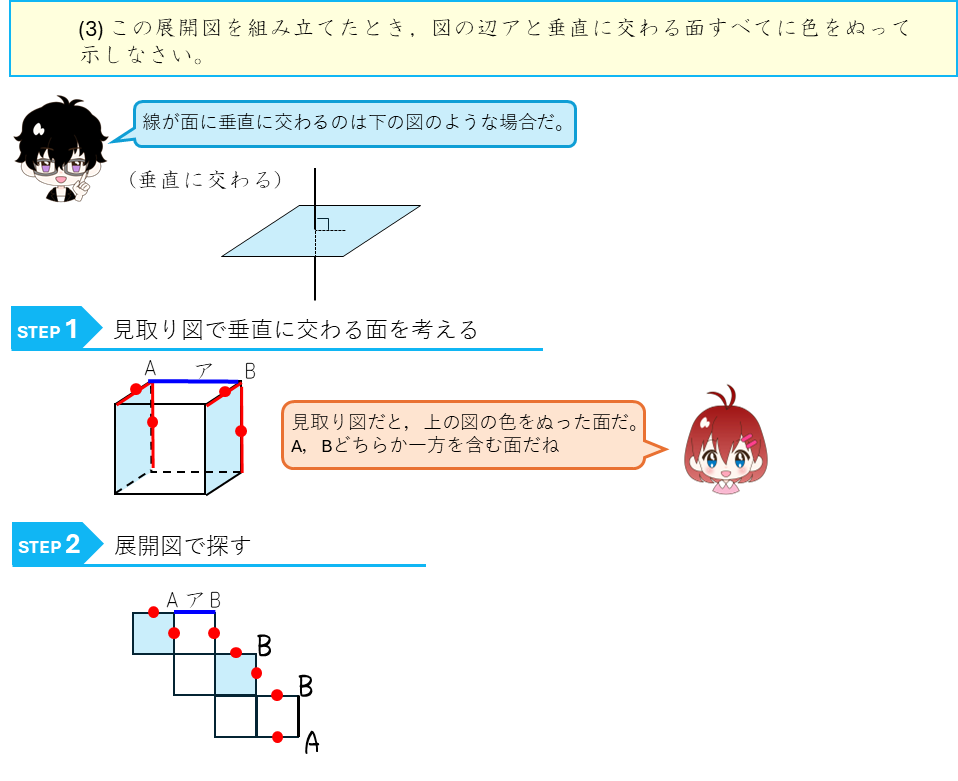
この問題で出てきた、線と平面の関係をまとめておくよ。線と平面の関係には、「平行」(どこまで行っても交わらない)、「交わる」、「ふくまれる」の3種類がある。この問題では、交わるの特別な場合である「垂直に交わる」が出てきたね。
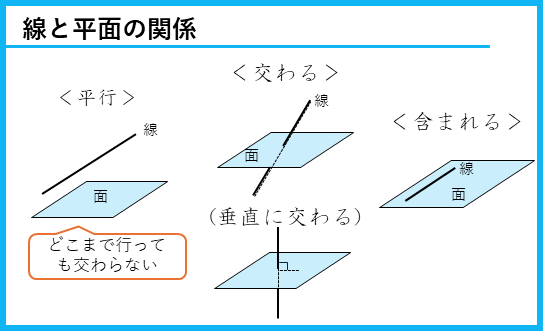
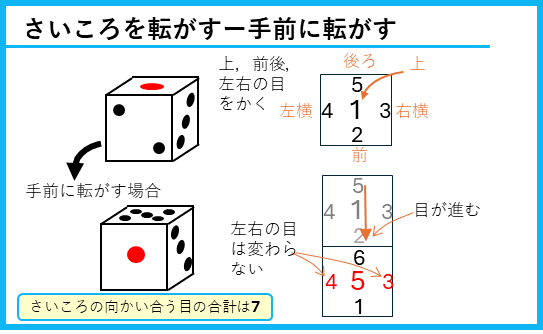
さいころを転がす

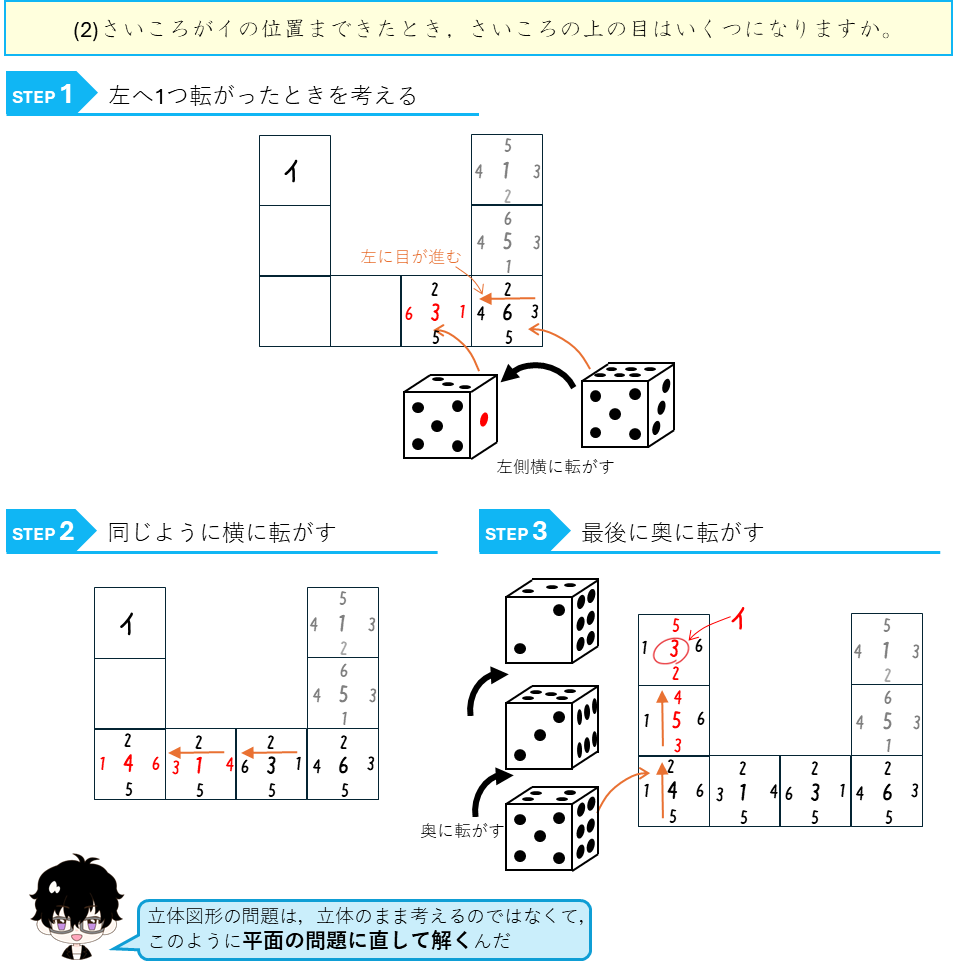
上からみた図をかいて解くという解法をカードとしてまとめておくよ。
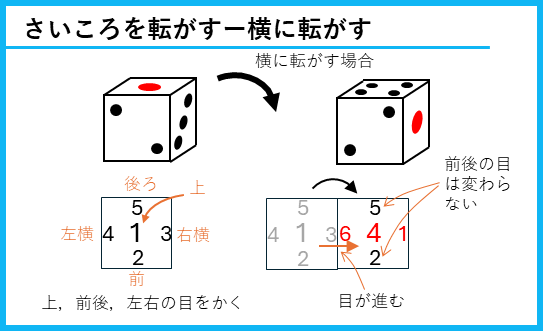
立方体を切り開く

コメント