
前回の単元では約数について勉強しました。この単元では、倍数について勉強していきます。倍数は、ある整数を1倍、2倍、3倍、…と整数倍した数です。□=〇×△(□、〇、△は0でない整数)の関係があるとき、□は〇、△の倍数となり、逆に、〇、△は□の約数という関係になります。共通の約数を公約数というように、2つ以上の整数に共通な倍数を公倍数といい、また、公倍数のうち最も小さいものを最小公倍数といいます。最小公倍数と最大公約数など混乱しないように、前回の約数と合わせて理解していきましょう。
(四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
解説
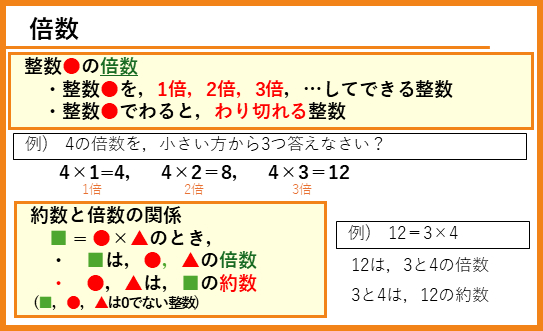
倍数
「整数●の倍数」とは、ある整数●を1倍、2倍、3倍、…と整数倍した数です。また、整数●でわり切れることができる整数とも考えることができます。
式で、
■=●×▲(■、●、▲は0でない整数)
とかくと、
整数■は整数●、▲の倍数 ⇔ 整数●、▲は、整数■の約数
という関係になります。倍数と約数の関係は理解できたかな?
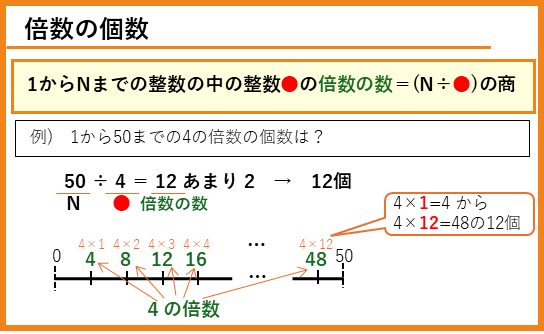
倍数の数を求める問題はよく出題されます。1からNまでの整数の中の整数●の倍数の数は
整数●の倍数の数 = (N÷●)の商
になります。例えば、1から50までの4の倍数の個数は、50÷4=12あまり2から、商の12個となります。4×12=48が、50以下で最も大きい倍数になるので、倍数の個数が12個ということも理解できますね。
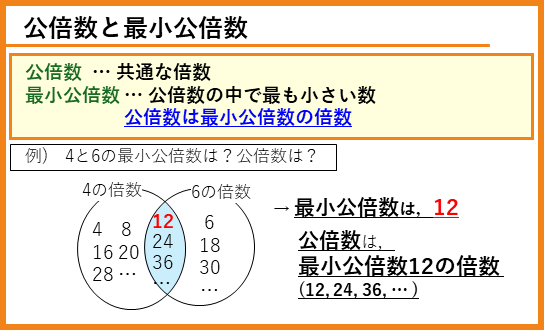
公倍数と最小公倍数
前回、2つ以上の整数の共通な約数「公約数」、公約数の中で最も大きい「最大公約数」について勉強しました。同じ考えで、2つ以上の整数の共通な倍数を「公倍数」、公倍数の中で最も小さい数を「最小公倍数」といいます。ここで、「公倍数は最小公倍数の倍数になる」ということも覚えておきましょう。
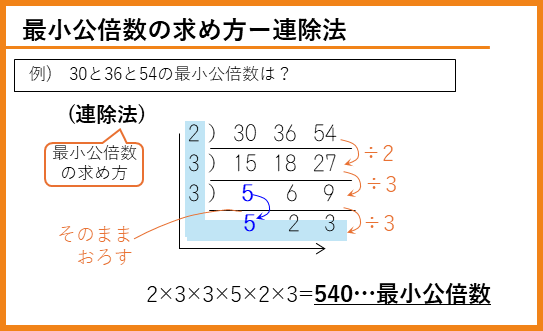
「連除法」によって、最大公約数を求めたのと同じように最小公倍数を求めることができます。最小公倍数の求め方では、かけ合わせる範囲や、3つ以上の整数の公倍数の求め方での最大公約数と違いがあるので注意しましょう。
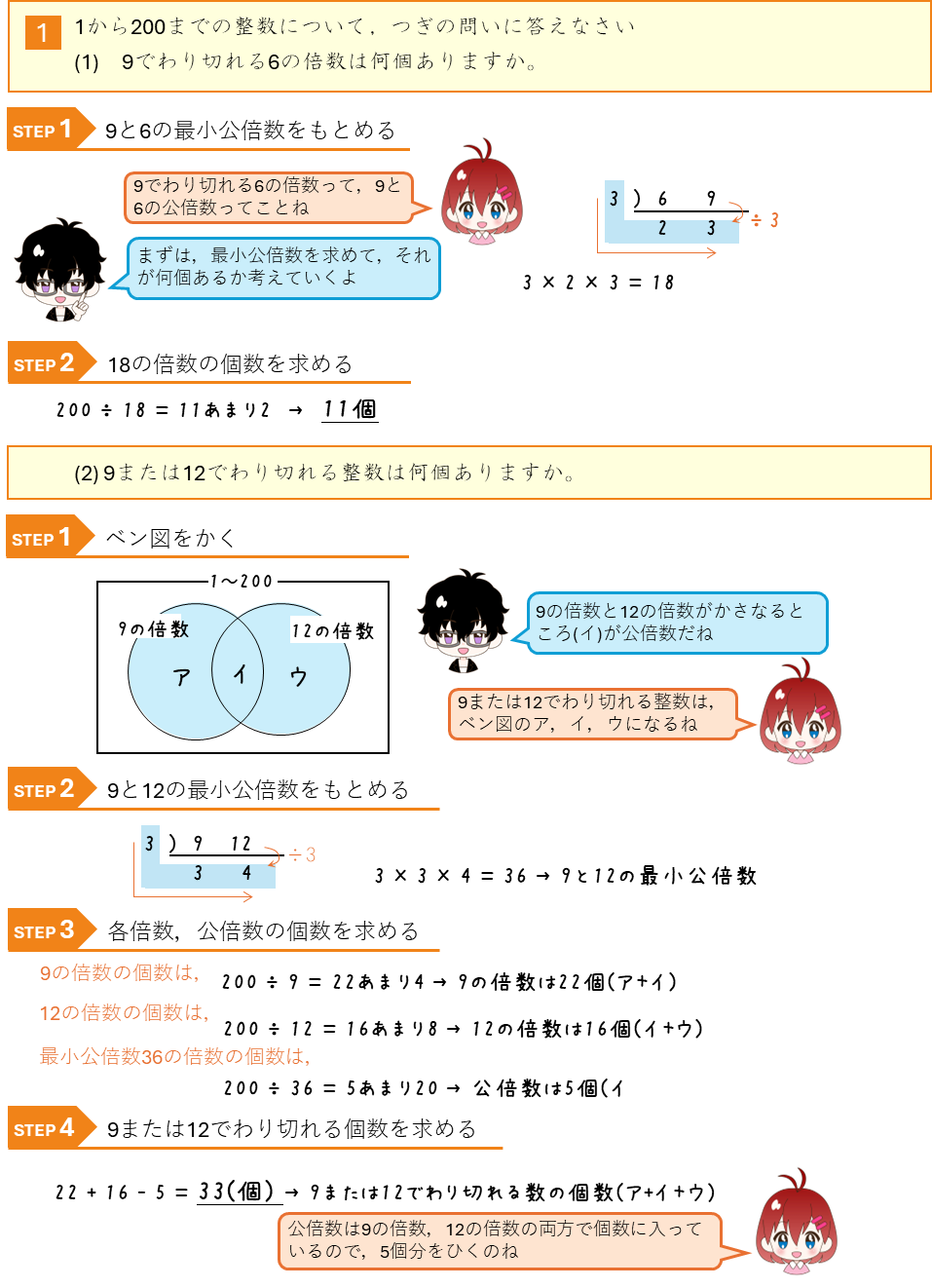
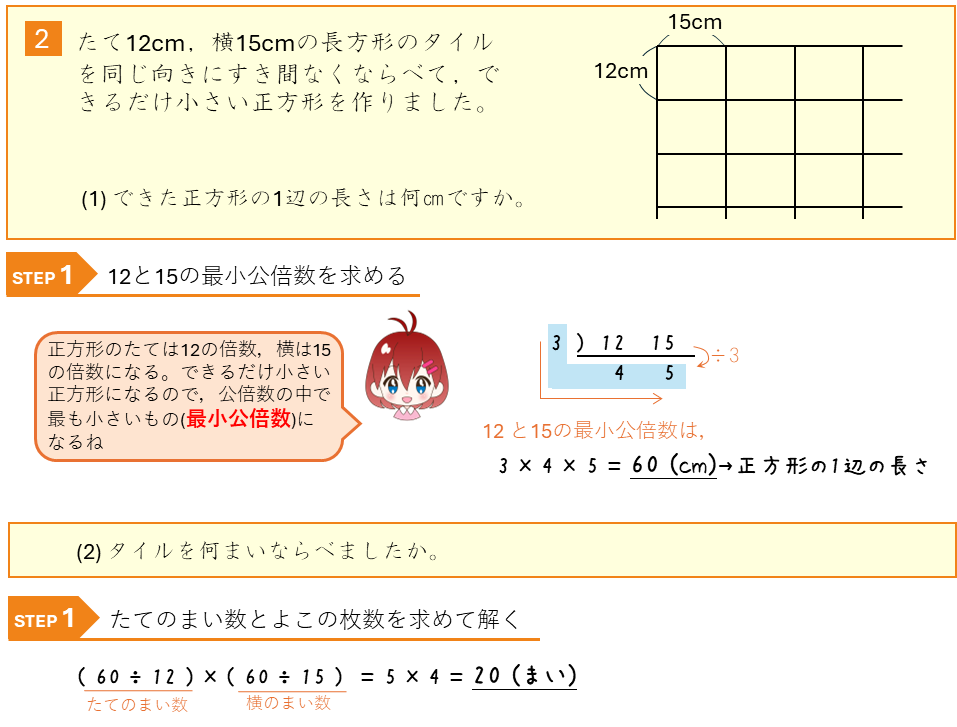
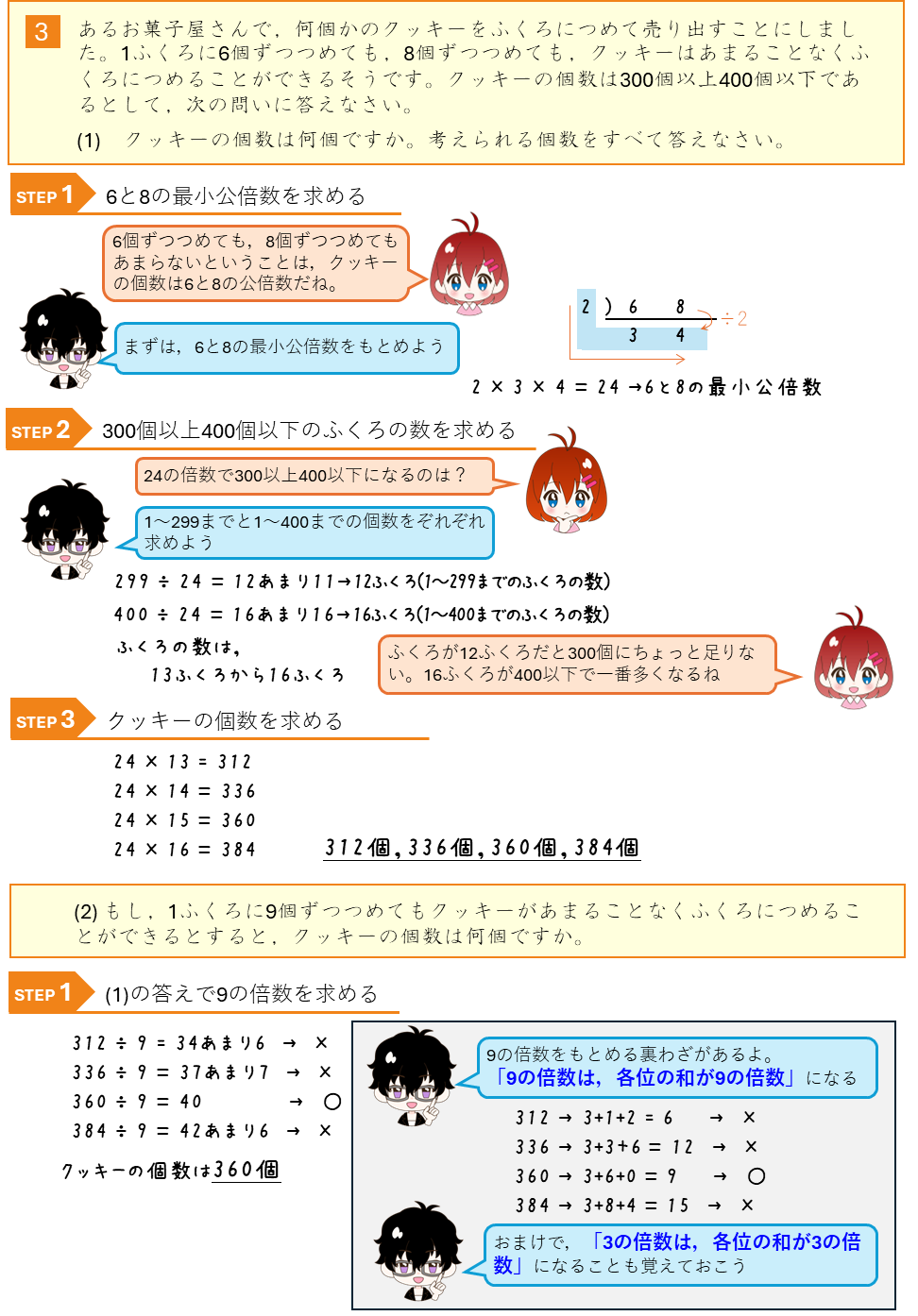
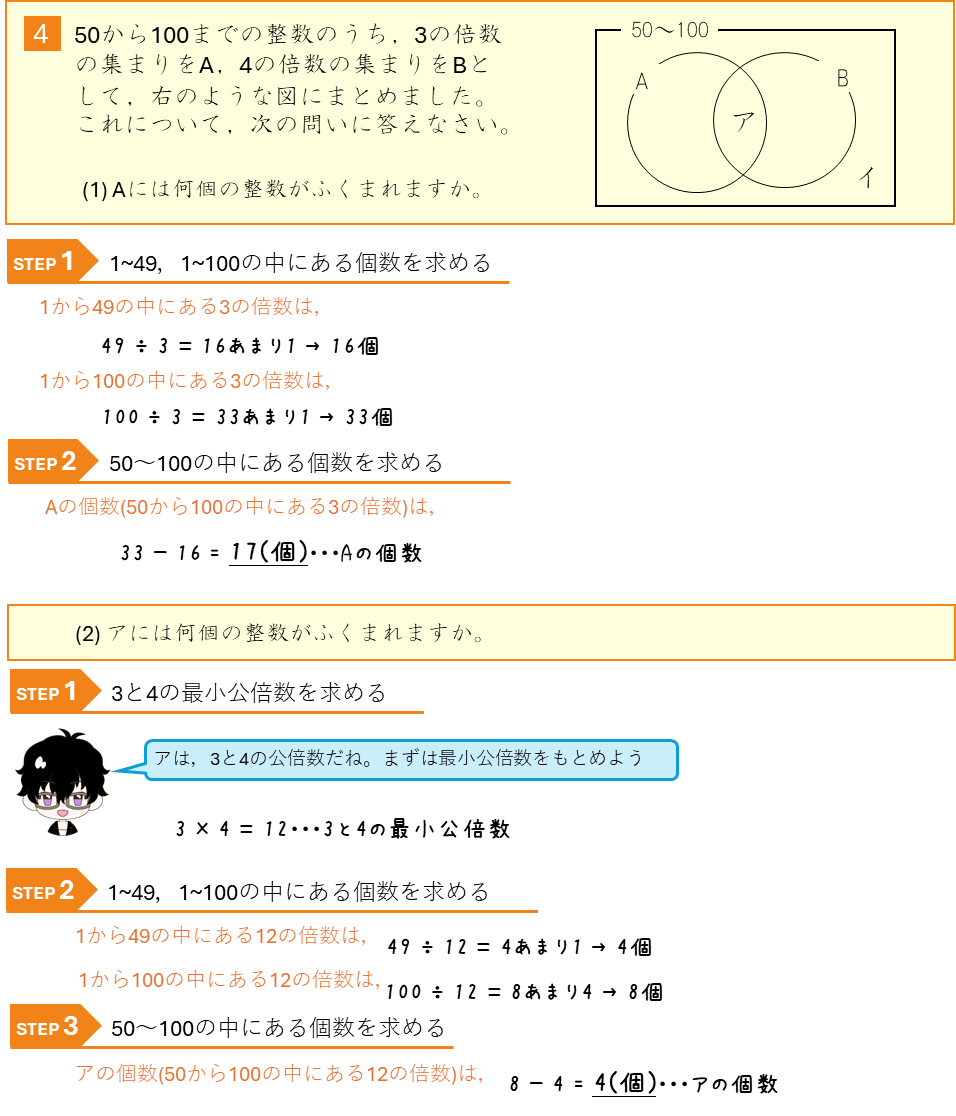
練習問題
公倍数の個数
最小公倍数を求める
最小公倍数とその個数
倍数・公倍数の個数
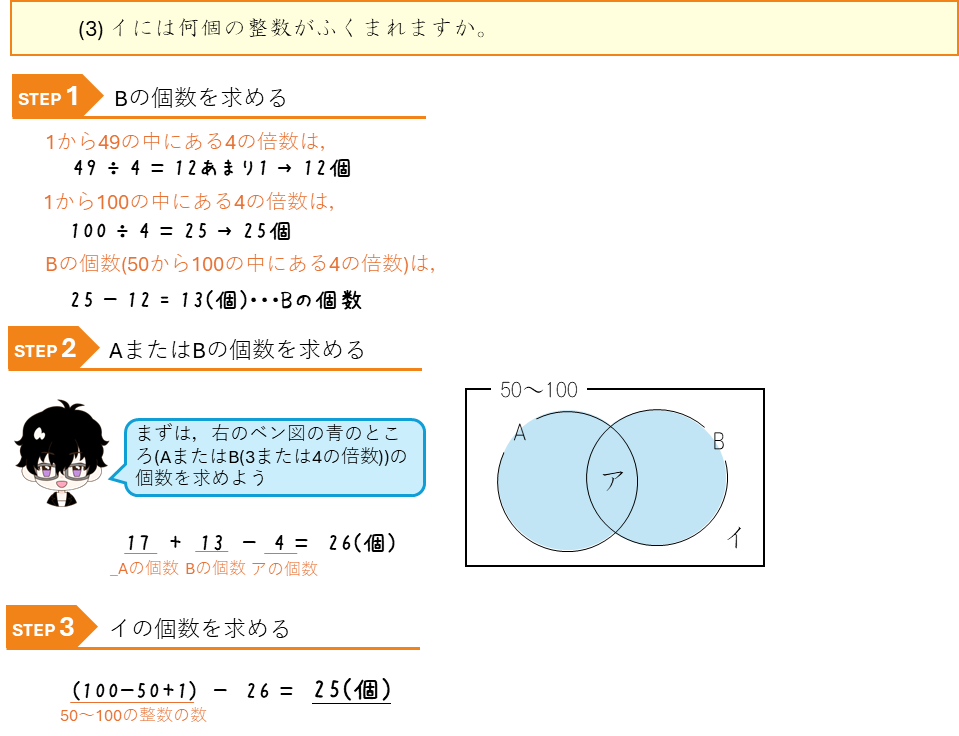
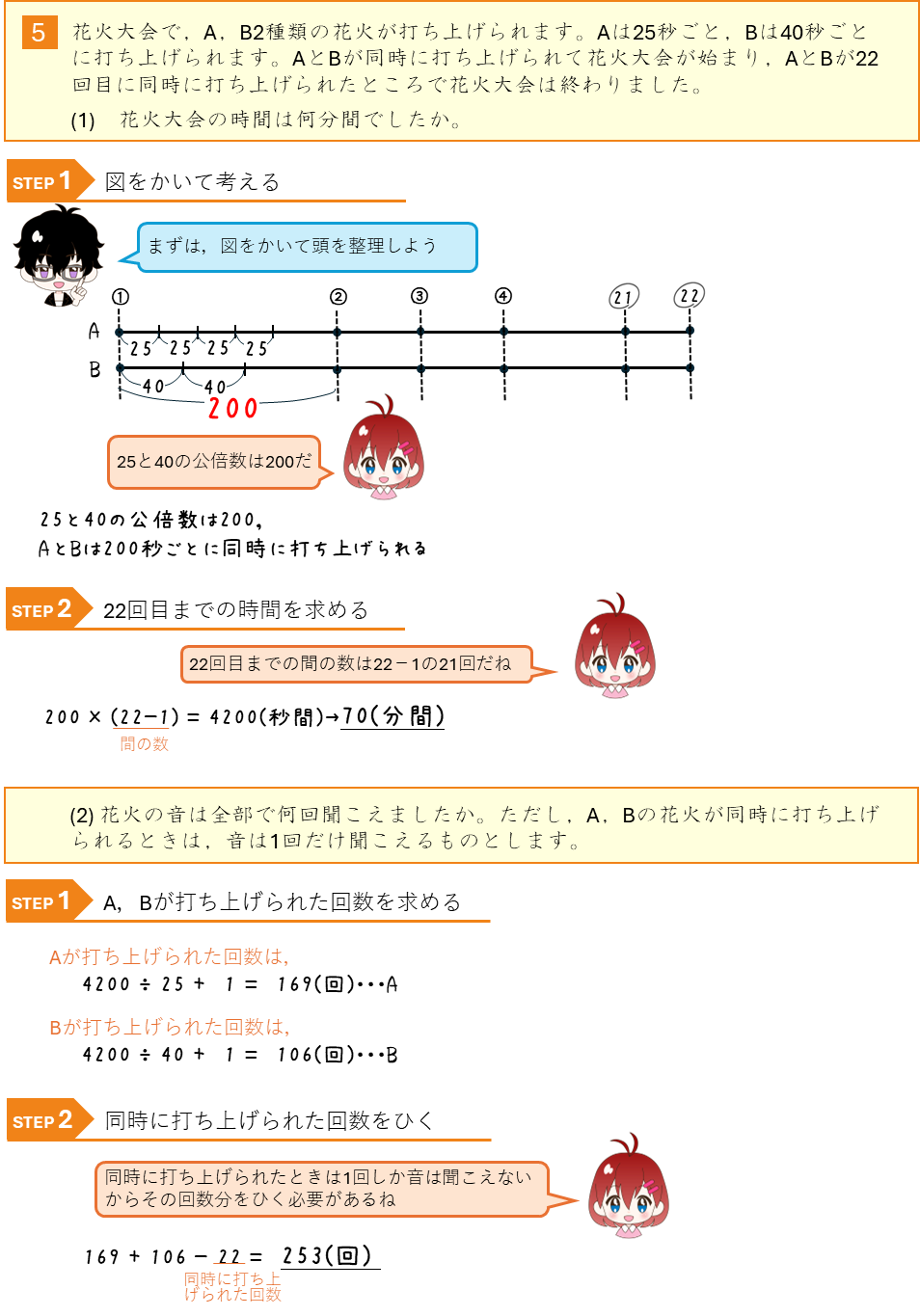
倍数の利用

コメント