
この単元では、数の性質の約数ついて勉強していきます。約数は、ある整数を割り切ることができる整数です。2つ以上の整数に共通な約数の公約数、それ以上割り切れない整数である素数などはじめて学ぶものがありますが、約数や公約数の求め方を覚えて、その性質を理解していきましょう。
(四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
解説
「約数」とは、ある整数を割り切ることができる整数のことです。この単元では、約数の求め方、素数、公約数と最大公約数を学んで、約数の性質を利用した問題をといていくきます。数の性質に関する問題は、イメージをもつのがはじめは少し難しいかもしれないけど、問題をときながら理解をふかめていきましょう。
約数
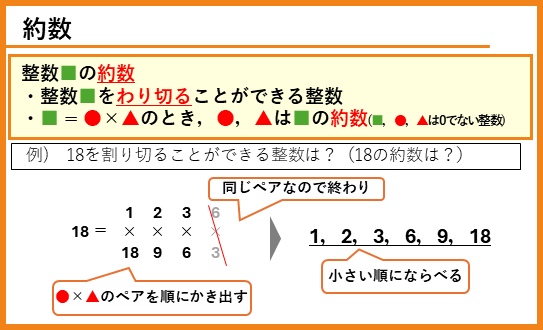
約数は、ある整数を割り切ることができる整数なので、ある整数□は、
■ = ● × ▲ (■、●、▲は0でない整数)
で表されるとき、●や▲は、■の約数になっている。したがって、約数の求め方は、かけ合わせると■になる●と▲のペアを見つけることになります。下の図のように、例えば18の約数を求める場合には、順に、(1×18)、(2×9)、…という風にぬけがないように書いていきましょう。(3×6)の次は(6×3)になりますが、すでに同じペアが出ているのでこの前まで終了です。あとは、小さい順に、1、2、3、6、9、18とかき出していけば完成。
素数
整数の中には、約数が1とその数自身の2個しかない、つまり、ほかの数では割り切ることができない数があります。例えば、2、3、5、7、11とか13です。これらの数は、「素数」と呼ばれています。約数を求める場合には、素数と素数のかけ算のペアを見つけたり、素数でわっていくので、ある数が素数かどうかすぐにわかるようにしましょう。
1から100までの素数をまとめておきます。丸暗記する必要はないけど、素数かどうかをすぐに判定できるようにしておきましょう。
2以外の2の倍数は素数ではない、3以外の3の倍数は素数ではない、5以外の5の倍数は素数ではない、7以外の7の倍数は素数ではないと、素数の倍数を消した残りが素数になります。
2以外の2の倍数(偶数)を消す、5以外の5の倍数を消すことから、2と5以外は、一の位は必ず1、3、7、9のどれかになります。さらに残りの数のうち素数は、3や7で割り切れない(3,7の倍数ではない)数であることに注意しましょう。特に、51(=17×3)、57(=19×3)、87(29×3)、91(=13×7)は素数ではないので気をつけましょう。

公約数と最大公約数
2つ以上の整数の共通な約数を「公約数」、公約数の中で最も大きい数が「最大公約数」といいます。

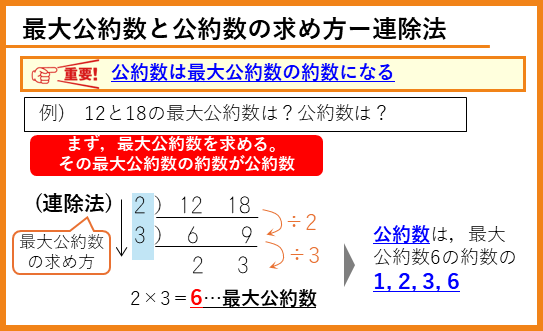
「公約数は最大公約数の約数になる」ことはしっかり覚えておきましょう。最大公約数をもとめる便利なやり方に「連除法」というものがあります。共通な約数をみつけて、順にわっていき、最後にその約数をぜんぶかけ合わせたものが、最大公約数になります。計算方法は難しいものではないので、使いこなせるようにしましょう。
公約数の求め方は、まず、この連除法で最大公約数を求めます。その最大公約数の約数が公約数になります。
互いに素
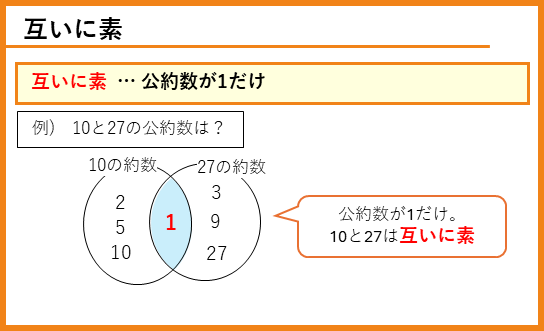
公約数が1だけの場合は「互いに素」といいます。
あまりがある数と約数
最後は、あまりがある数です。
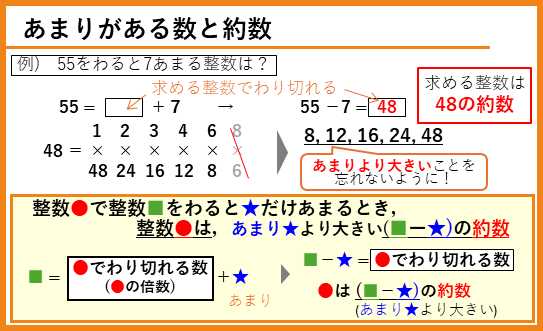
55をわると7あまる整数を考えると、55からはんぱの7をひいた48はわり切れる数になることが分かります。したがって、求める整数は48の約数になります。ここで、7あまるので、約数のうちの7より大きい整数になることを忘れないようにしましょう。
「はんぱ(あまり)をひけば、わり切れる(つまり、約数)」ということをイメージできるようにしよう。
練習問題
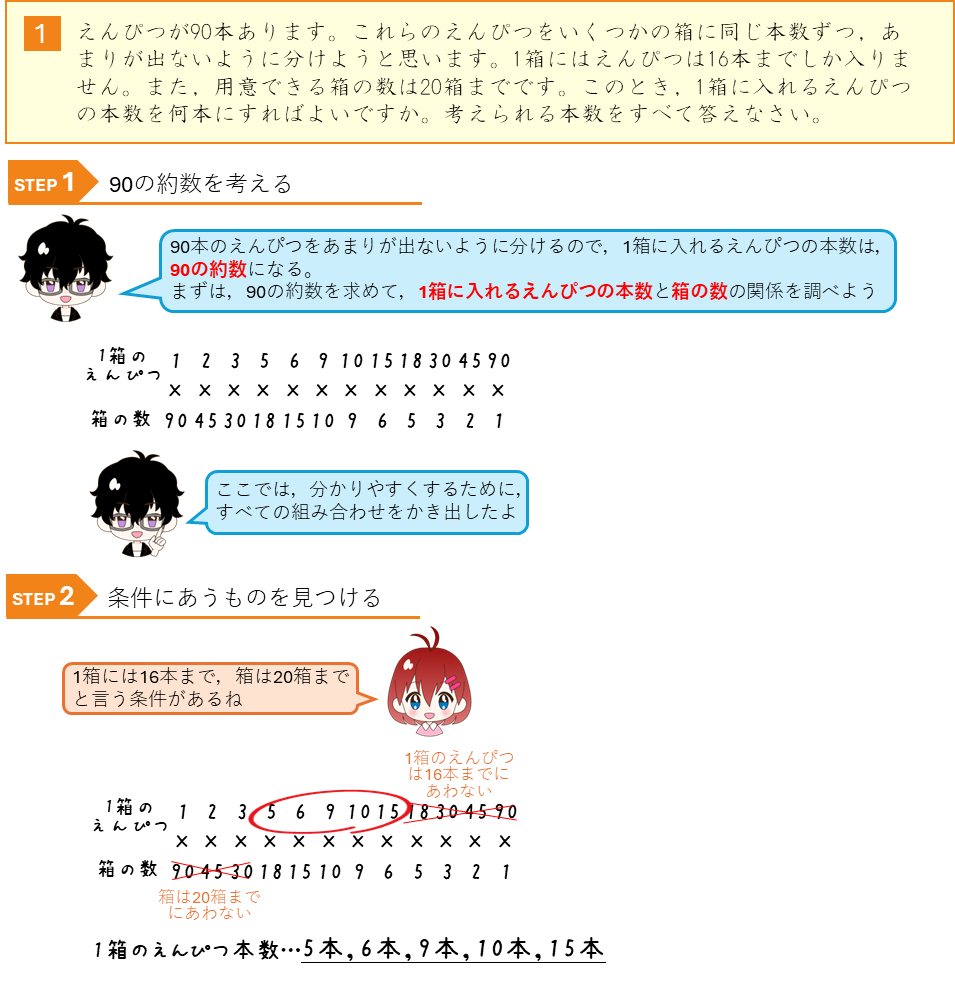
約数ー条件にあうものを見つける
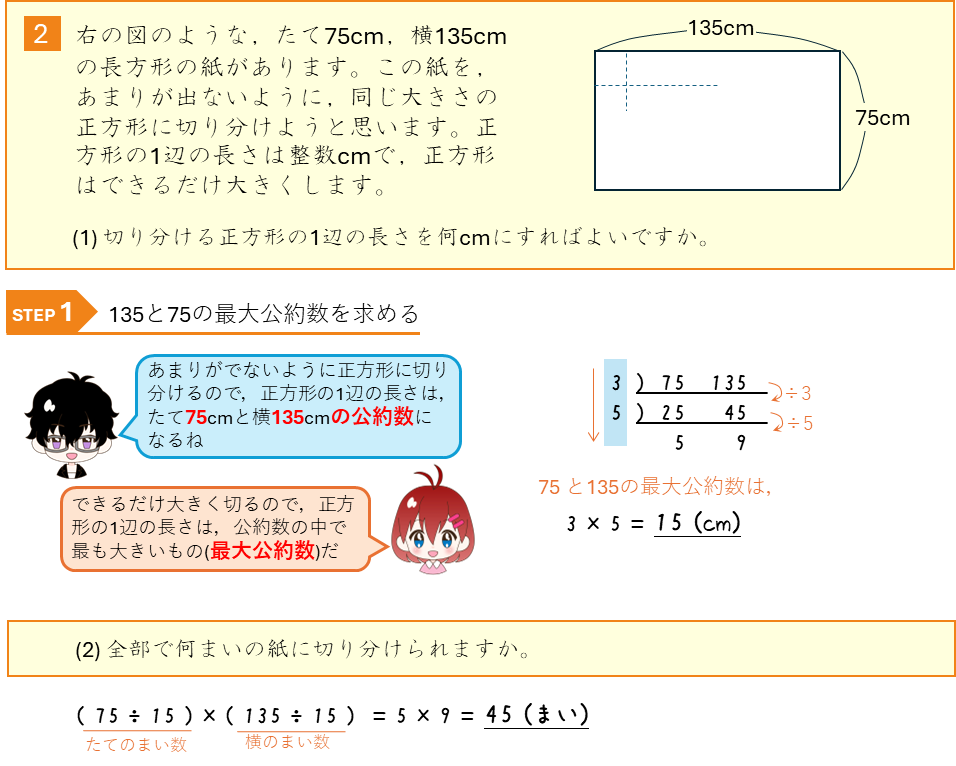
最大公約数を求める
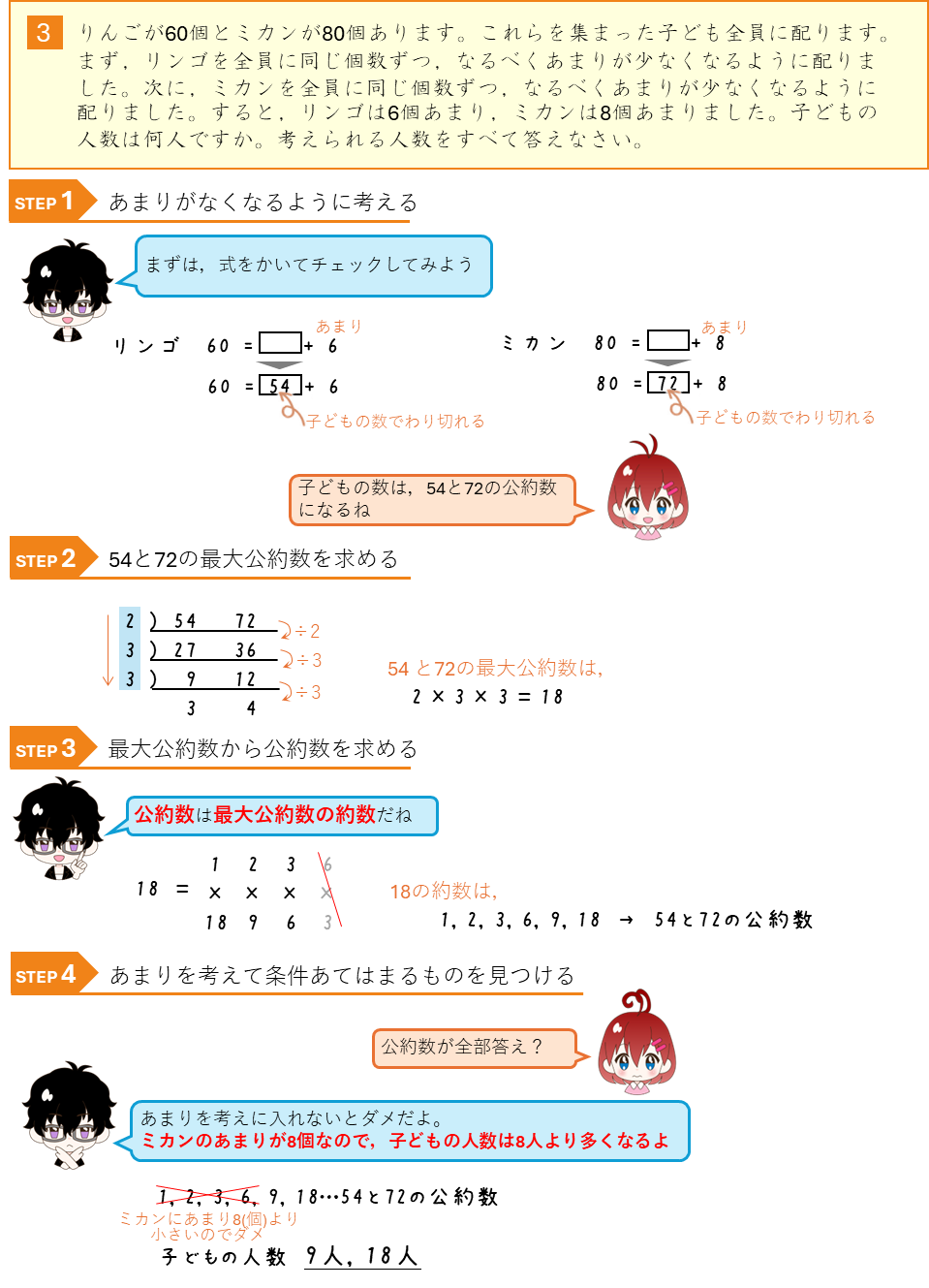
あまりがある数の公約数
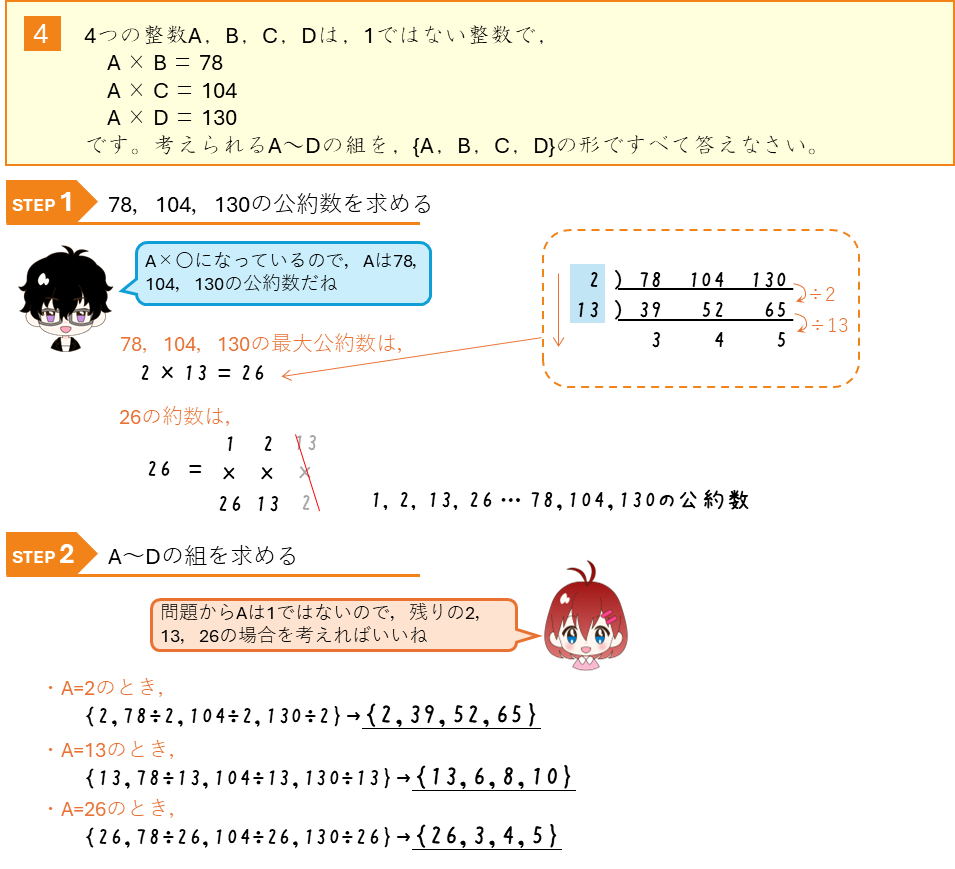
3つの数の公約数
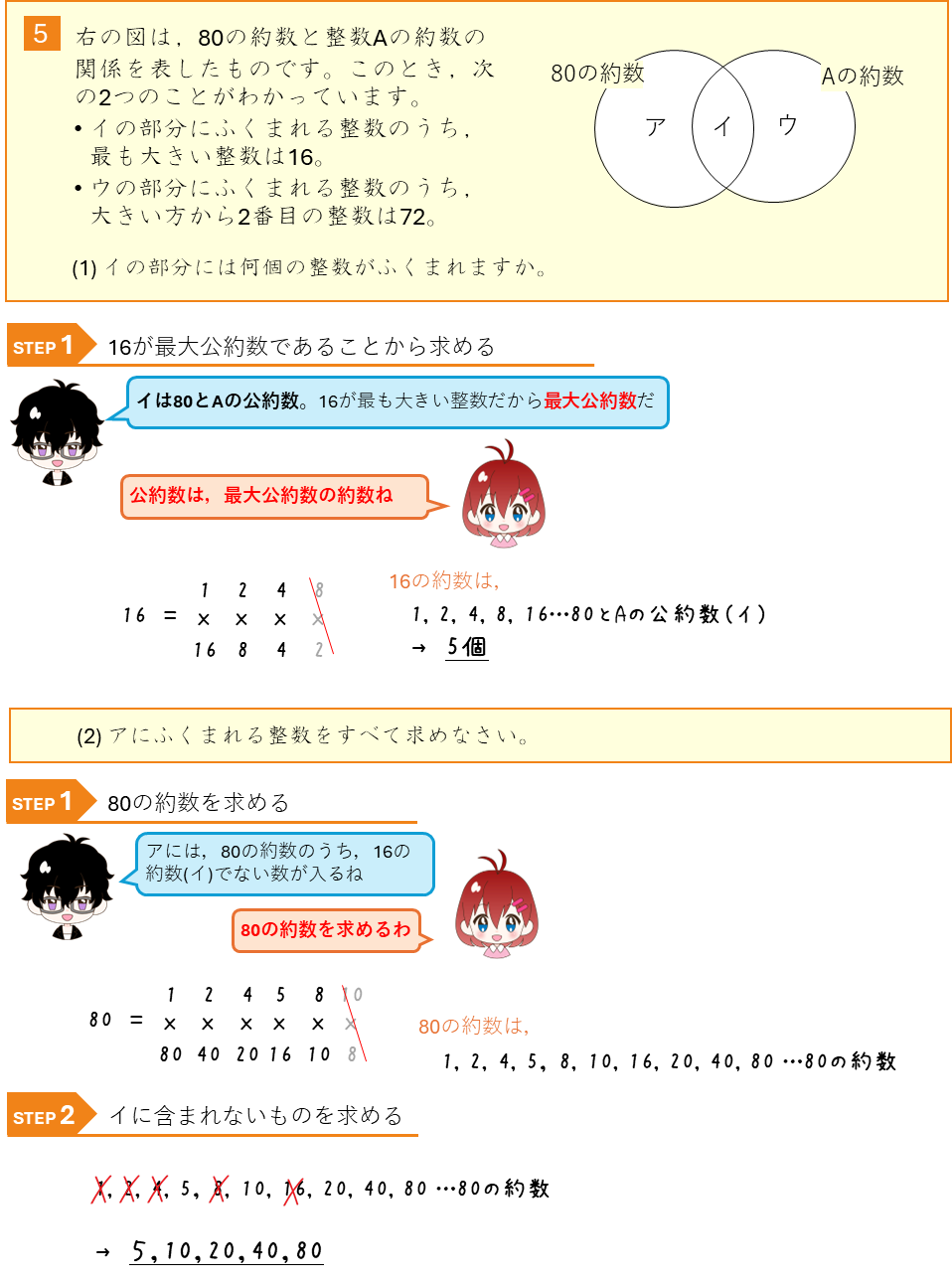
公約数ーベン図


コメント