この単元では、数のならび(数列)の一つである「等差数列」について勉強していきます。等差数列はその名前の通り、次の数との差が等しい数列です。その性質から何番目の数の値や数列の和を求めることができます。公式を丸暗記してしまうのではなくて、その原理をよく理解しておきましょう。図をかいてイメージをつかんでください。また、奇数をならべた数列は等差数列の特別なものです。特に、その和が平方数(NxN)になることを覚えておきましょう。（四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
- 2024年6月27日 解説などを更新
解説
数のならび(数列)の一つの「等差数列」について勉強していくよ。等差数列は、「はじめの数から一定の数を次々と加えたり、ひいたりして作られる数列」だよ。一定の数を「公差」と呼ぶので覚えておこう。
等差数列の線分図をかいてみよう。 7, 10, 13, 16, 19, ……を例に考えるよ。
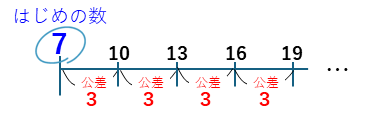
はじめの数7から、公差の3だけ増えていくね。じゃあ、問題です。
等差数列ーN番目の数を求める
これも図をかいて考えよう。上の図を10番まで伸ばしてみるよ。
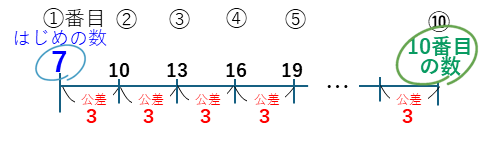
この図から、10番目の数を求めていこう。まず、１番目から10番目の間の数(公差の数)はいくつあるかな？
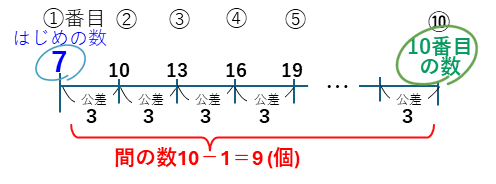
１番目から10番目の間の数(公差の数)は10－1＝9個だね。したがって、1番目から10番目までは、
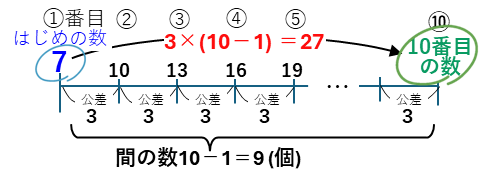
3×9＝27だけはなれている。これで、もう10番目の数は分かった！ 7＋27＝34だ。
この問題は、植木算と同じに考えられるね。
木をスタート地点から順に植えていきます。はじめの1本をスタート地点から7mの位置に、それから10m、13m、16m、19ｍと等しい間かくで植えました。10本目の位置はスタート地点から何mですか？
図でかくと、
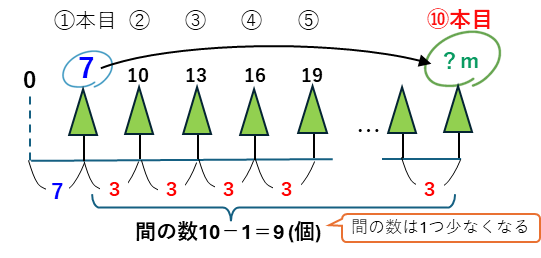
となるね。これは等差数列の線分図と同じ。間の数は、10－1＝9個。間の長さは3mなので、1本目と10本目までは、3×9＝27(m)だけはなれている。したがって、10本目の位置は、スタートから7＋27＝34(m)となるよね。これは、等差数列の10番目を求めるのと一緒だ。等差数列は数だけなのでむずかしいかもしれないけど、植木算と同じと考えればイメージしやさすくなると思うよ。
N番目の数の公式
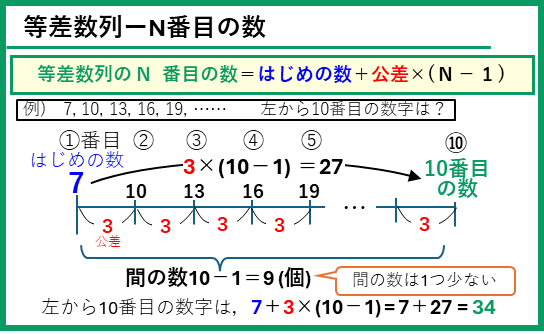
公式でかくと、等差数列のＮ番目の数は、
Ｎ番目の数 = はじめの数 ＋ 公差×(Ｎ-１)
となる。これを公式として丸暗記しても忘れてしまうので、はじめはかならず図をかいて解いていこう。そうすれば自然と公式を身につけることができるよ。
あと、等差数列は、階段の高さとしてもイメージできるようになるといいよ。
このイラストみたいに、最初のステップだけ高さがちがう階段をイメージしてみよう。階段の高さを順にならべたものが等差数列になるよ。
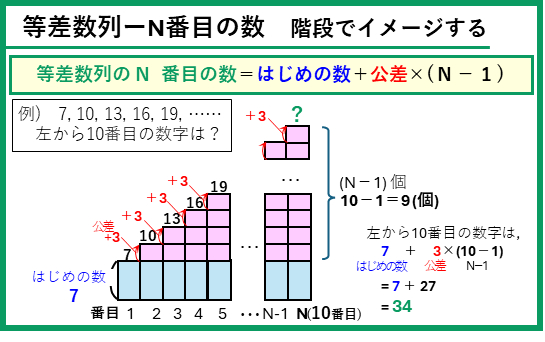
階段の１段目の高さが「はじめの数」で、２段目以降のステップの高さが「公差」になるね。2段目以降のステップの数は、最初の段をのぞいたN-1段となるね。これから、Ｎ段目の高さは等差数列の公式になることがわかるよね。
等差数列ー何番目かを求める
等差数列の問題として、数列の値からその番号を求めるものもよく出題されるよ。これも線分図をかいてとけるようになろう。
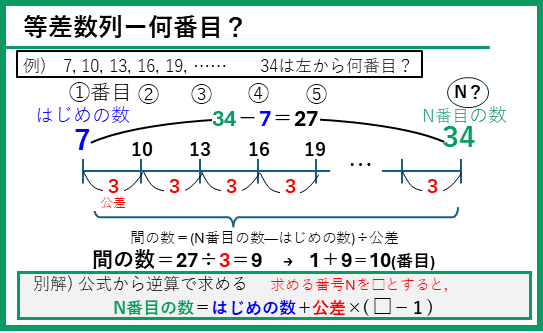
別のとき方として、等差数列の公式から逆算で求めるやり方もある。これは等差数列と逆算がしっかり身についてから使っていこう。
等差数列の和
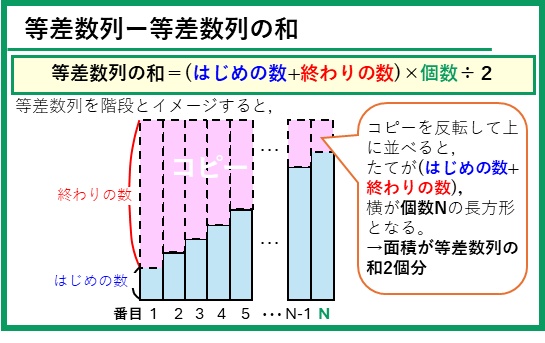
等差数列の問題として、等差数列の和を求めるものもあるんだ。等差数列のそれぞれ数に逆順の数を足すと一定になるという性質を利用して、
等差数列の和 = (はじめの数+終わりの数)×個数÷２
と言う式で求めることができる。下の図ように、等差数列の階段をコピーして反転してならべると、たてが(はじめの数＋終わりの数)、横が数列の個数Ｎの長方形となることをイメージしよう。この長方形は数列２個分なので、数列の和は、その面積の半分として計算できる。
奇数をならべた数列ー平方数
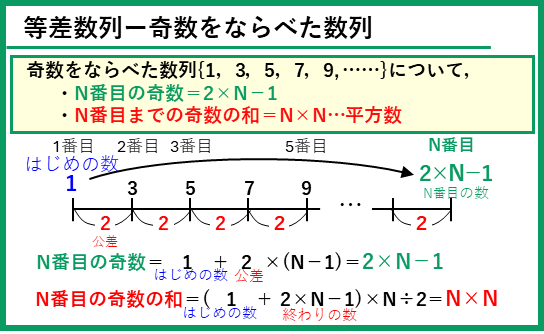
最後に、奇数をならべた数列について説明するよ。奇数をならべた数列は「１からはじまり、公差が２」の数列と考えられるので、等差数列の公式を使うことができるけど、特に、
Ｎ番目の奇数＝２×Ｎ-１
Ｎ番目までの奇数の和＝Ｎ×Ｎ（平方数）
と、もっと簡単な式で計算できる。特に、奇数の和は、同じ数をかけ合わせた数（平方数）となることはよく覚えておこう。
練習問題
等差数列の基本問題
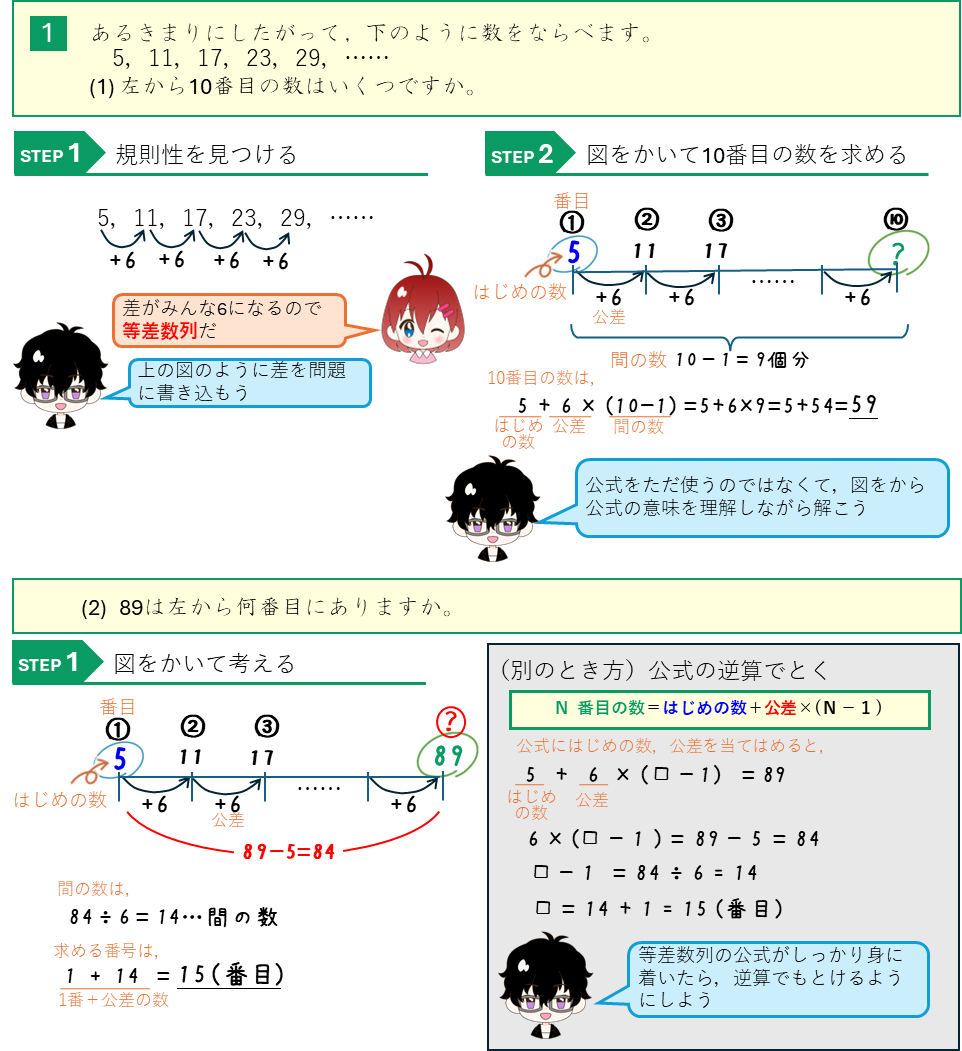
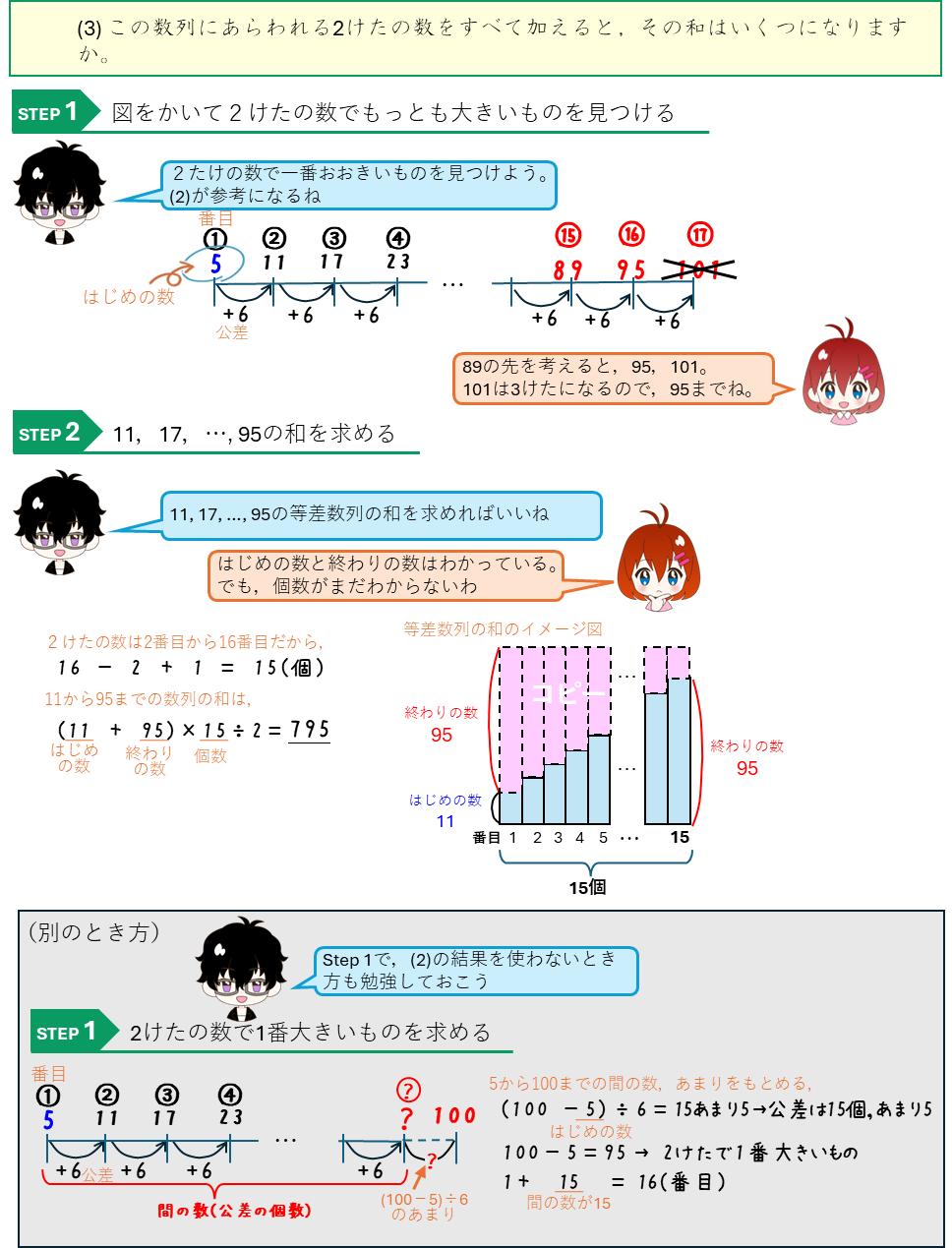
等差数列ーＸＸ以下で最も大きい数
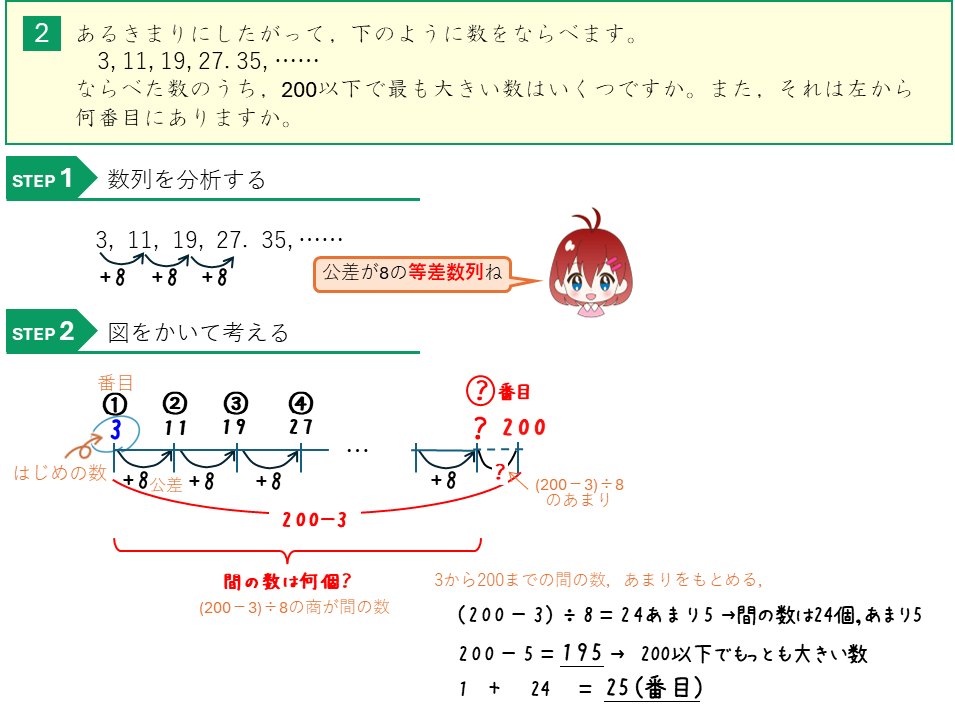
等差数列ーテープをつなげる
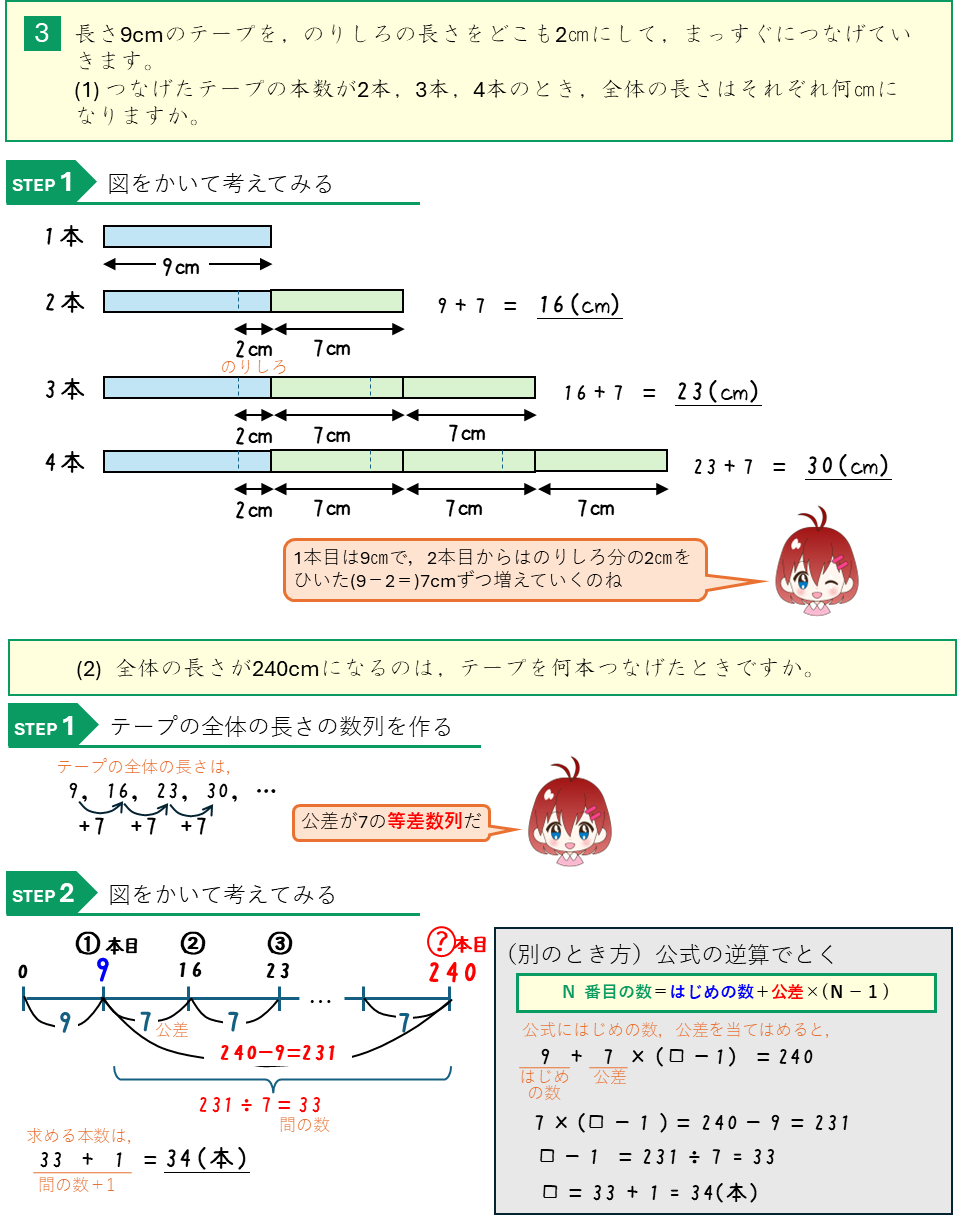
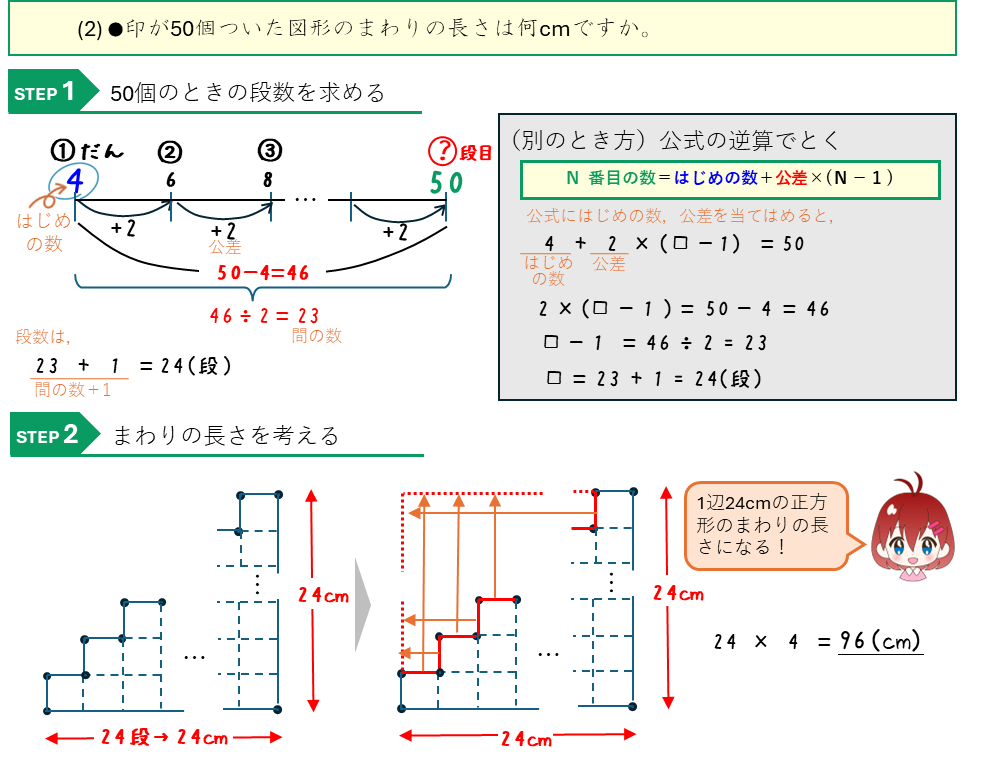
等差数列ー図形の問題
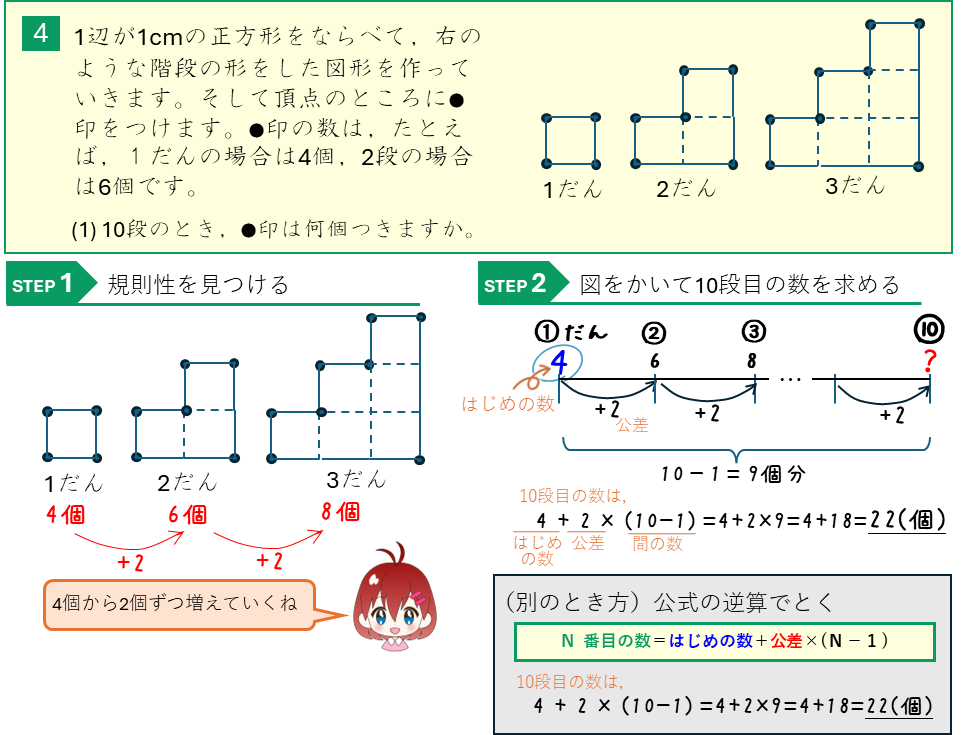
等差数列ー奇数をならべた数列
コメント