この単元では、文章題の「周期算」について勉強していきます。くり返し(周期)を見つけて問題をといていきます。ご石のならび、数字のならび、図形などいろいろな問題がありますが、周期1つ分の個数や和から、周期の数やはんぱを計算してといていきます。はじめは難しい感じがするかもしれませんが、基本の考え方は同じですから問題をといて基礎をかためましょう。(四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
解説
周期算ー個数の公式
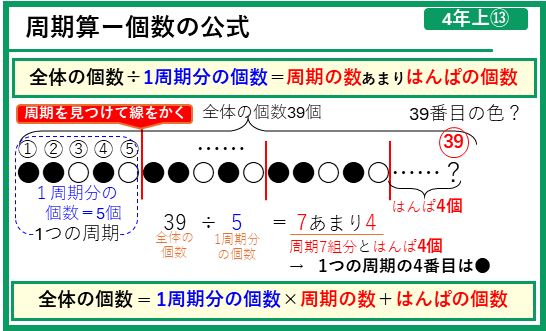
くり返し(周期)をみつけて問題をとく「周期算」について勉強していくよ。「全体の個数」を「1つの周期あたりの個数」で割ると、何周期分あるか、つまり「周期の数」が分かるよ。割り切れなかったときは、あまりは1つの周期の一部の「はんぱの個数」となるね。
全体の個数 ÷ 1周期分の個数 = 周期の数 あまり はんぱの個数
逆に、「1つの周期の個数」と「周期の数」、「はんぱの個数」がわかれば次の式から、「全体の個数」を求めることができる。
全体の個数 = 1周期分の個数 × 周期の数 + はんぱの数
周期算ー和の公式
数字がならぶ(数列の)問題では、数の和で考えていくものもあるよ。周期をみつけたらその「1つの周期の数の和」を求めよう。「全体の和」をこの「1つの周期の和」で割ると、「周期の数」がわかる。このとき割り切れなかったあまりは、「はんぱ分の和」になるね。
全体の和 ÷ 1周期分の和 = 周期の数 あまり はんぱ分の和
公式として丸暗記するのではなくて、自然と使えるようになるように問題をといて身に着けよう。

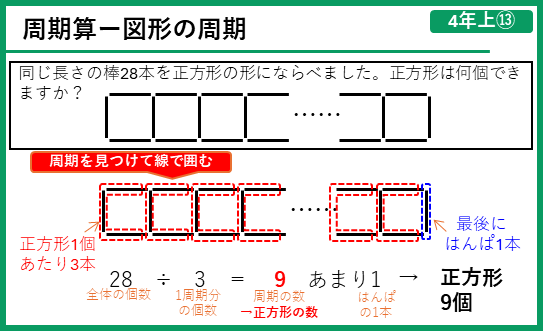
周期算ー図形の周期
同じ形がくり返し続く図形に関する問題でも、周期を見つけて解いていくよ。
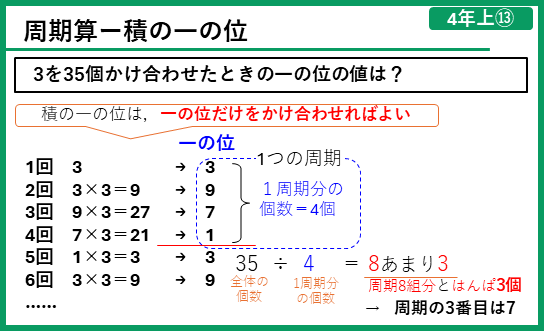
周期算ー積の一の位
積の一の位は、一の位だけをかけ合わせることで求められます。積の一の位の値を求める問題では、このことを使って、積の一の位を計算してその周期を見つけて解きます。
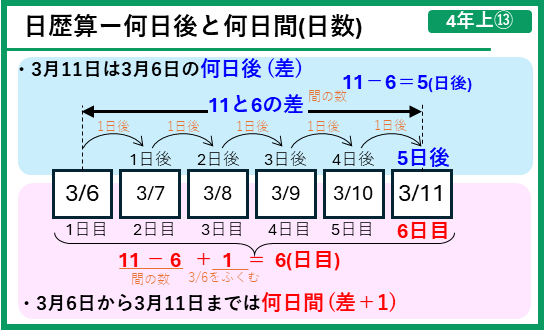
日歴算
日付や曜日に関する問題を「日歴算」と言います。日歴算について覚えておくことをまとめます。
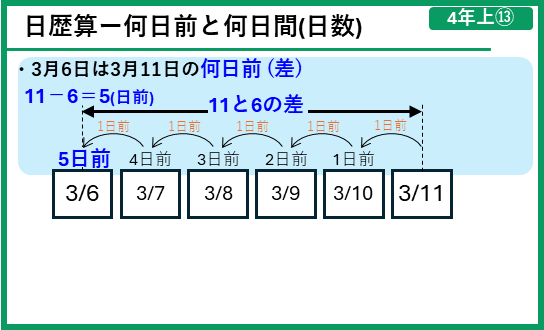

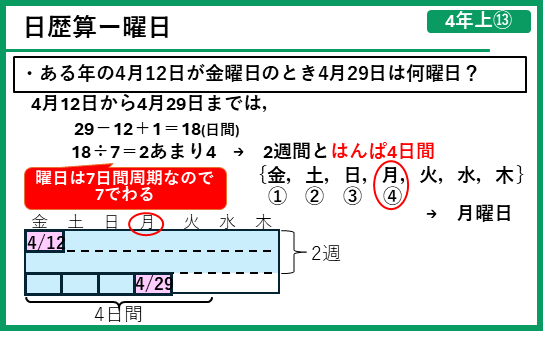

練習問題
周期算ー数の並び
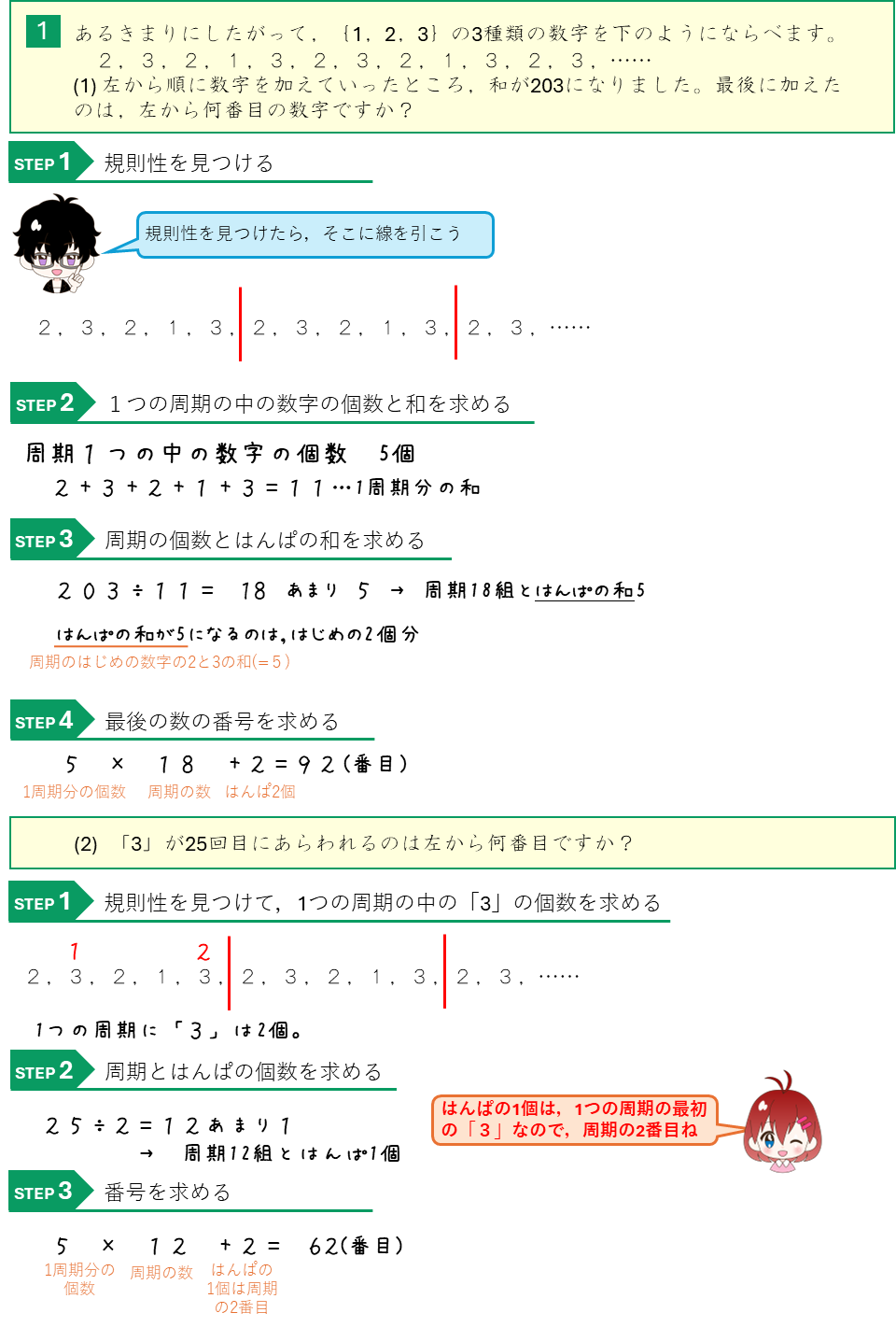
周期算ー積の一の位の約束記号
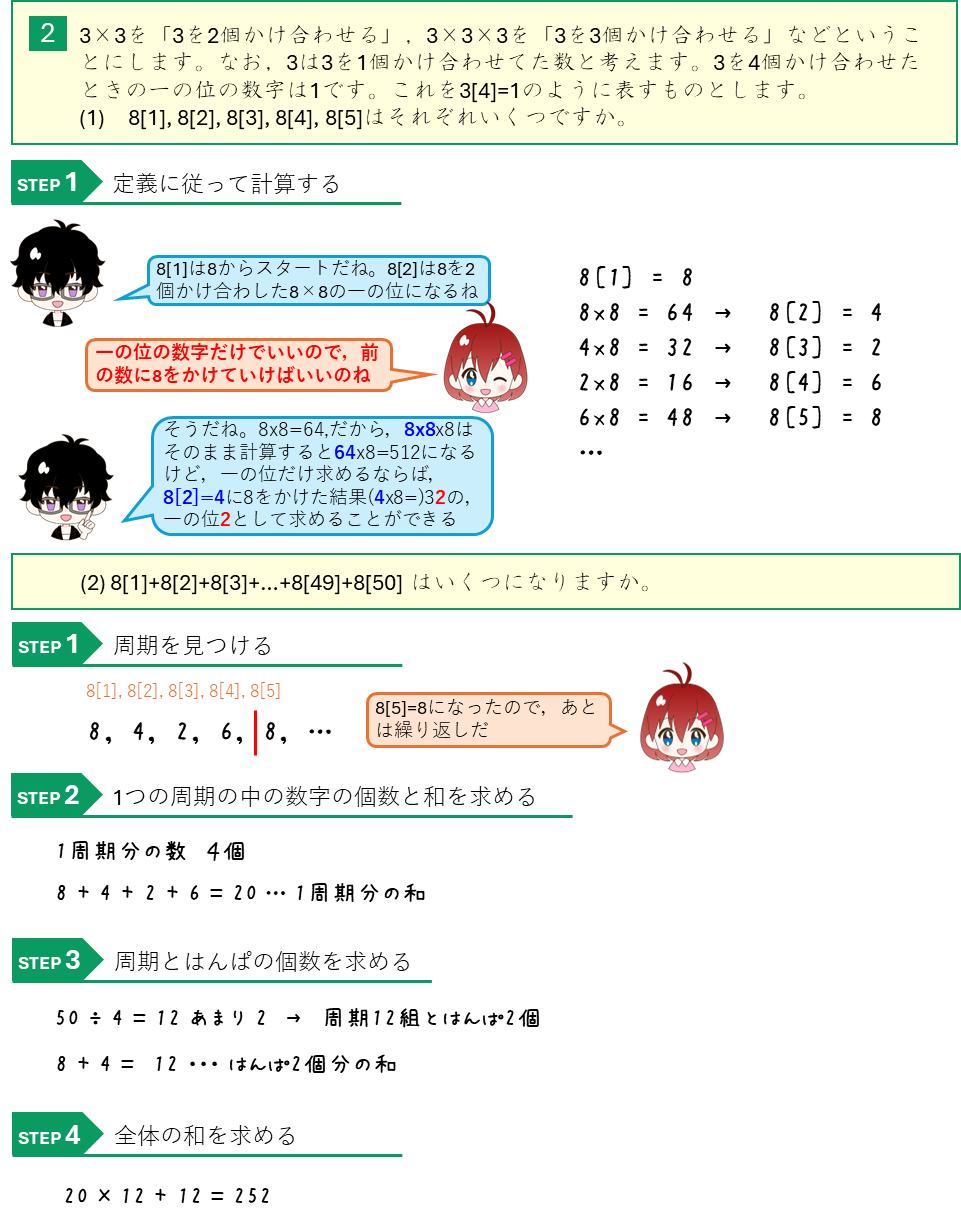
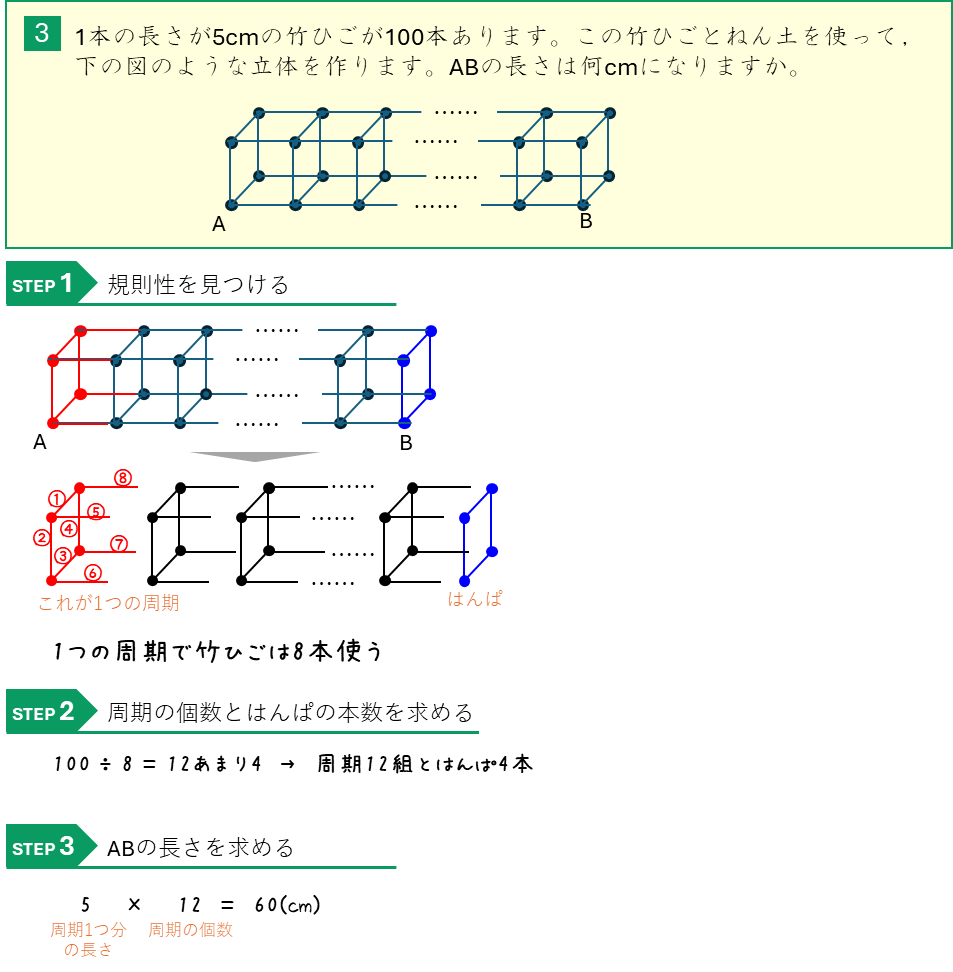
周期算ー図形の周期
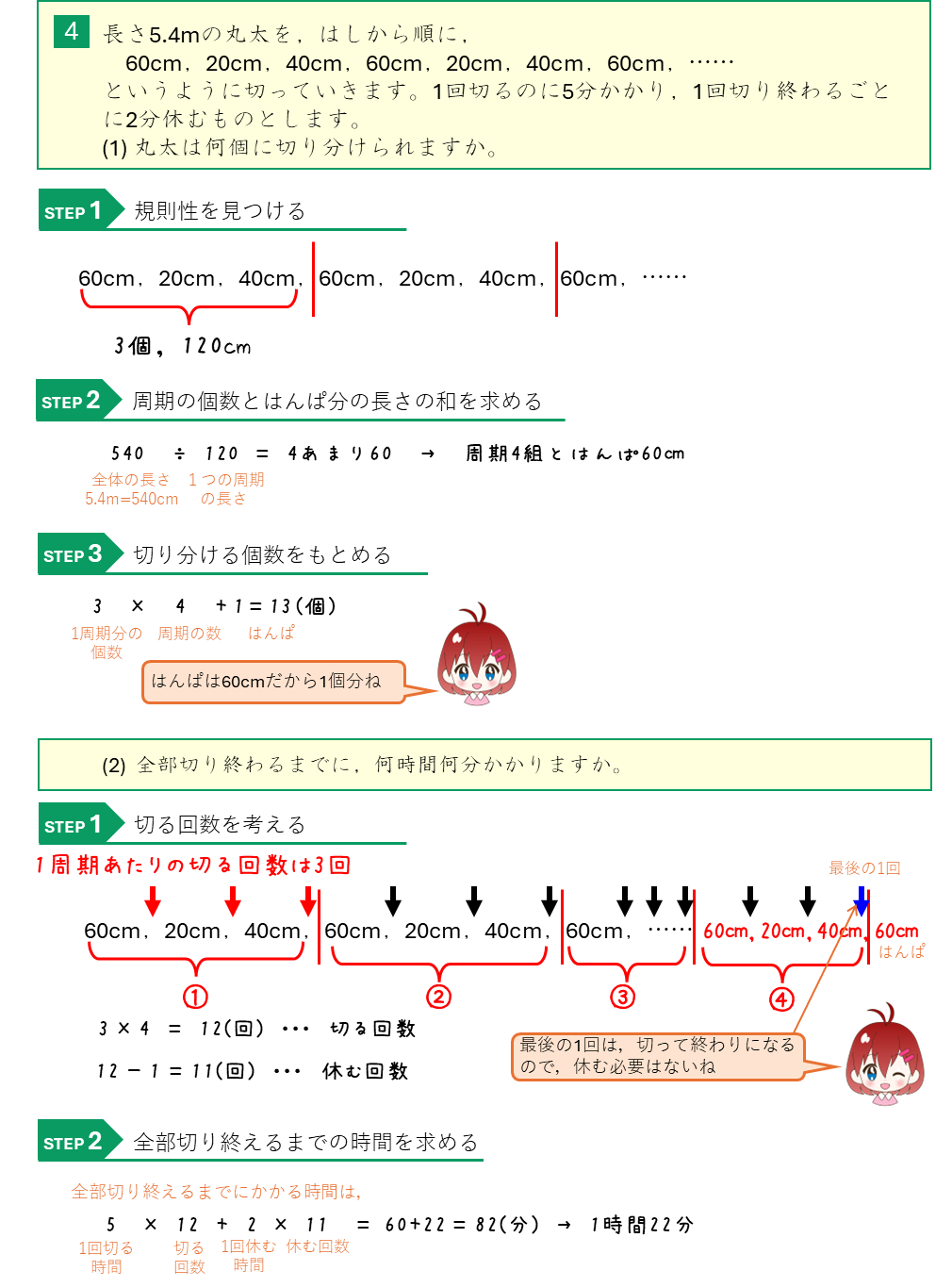
周期算ー丸太を切って休む
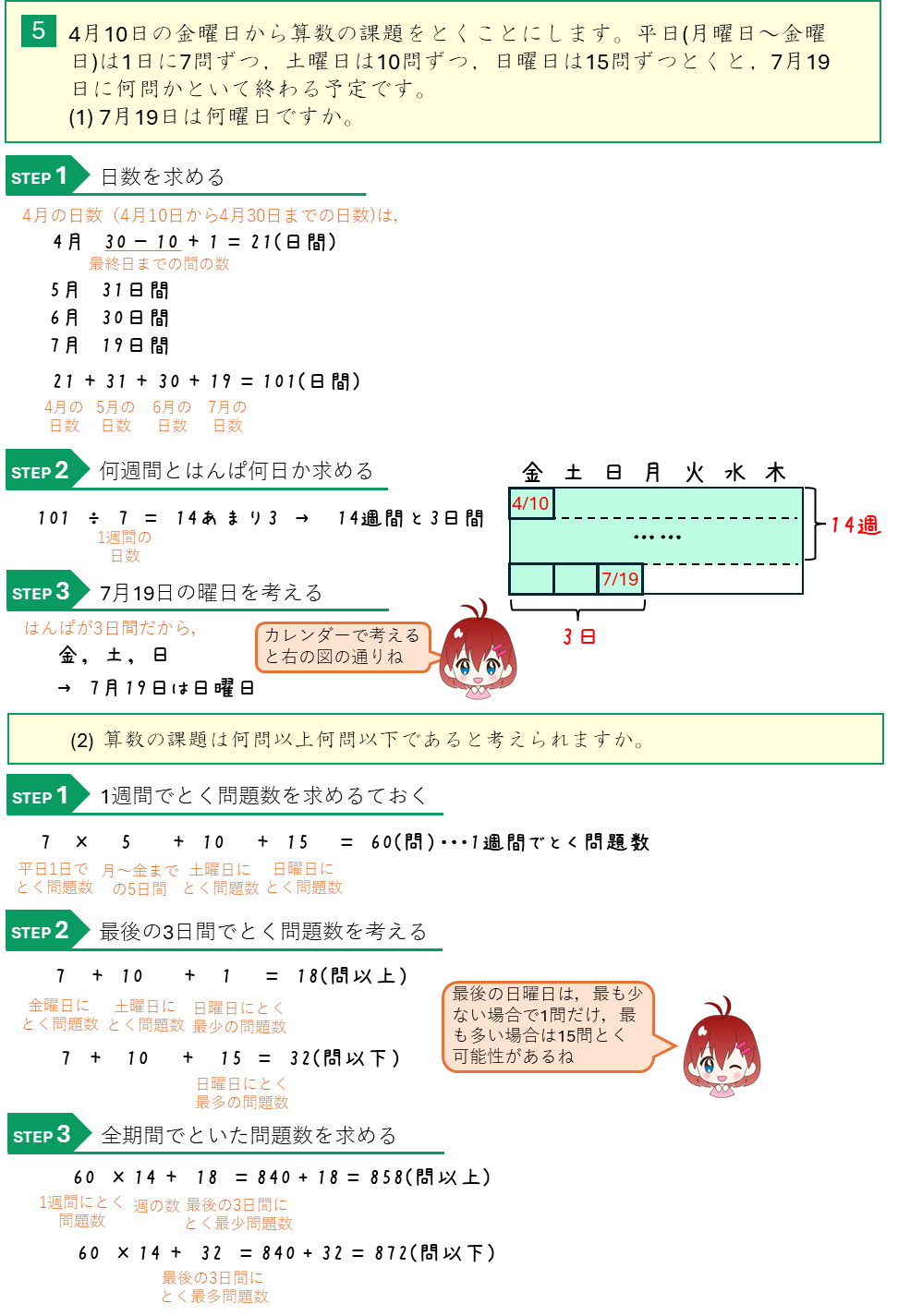
日歴算-日数・曜日を求めて考える

コメント