
今回は、分数について勉強します。 分数は、ある大きさを〇等分したときの1つ分の大きさを$\frac{1}{〇}$と表したものです。$\frac{1}{〇}$が2つで$\frac{2}{〇}$、$\frac{1}{〇}$が3つで$\frac{3}{〇}$、、、となることをしっかり理解しましょう。
単位のついた分数では、$\frac{1}{5}$mや、$\frac{3}{4}$時間などをcmや分になおして計算することを学びます。
また、分数の表し方の真分数、仮分数、帯分数では、仮分数と帯分数の変換について学びます。上の分数の意味から、変換についても理解できると思います。
分数もまた、様々な問題の計算にでてきますので、ここで原理から理解することが大切です。
(四谷大塚 予習シリーズ算数 四年上の解説です。テキストは四谷大塚から購入してください。)
解説
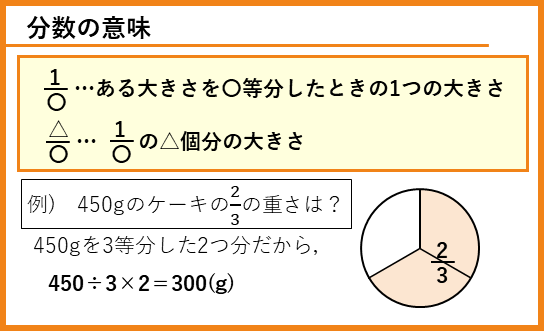
分数の意味
分数では、例えば、ある大きさを5等分したときの1つ分の大きさを$\frac{1}{5}$と表します。この$\frac{1}{5}$2個分で$\frac{2}{5}$、$\frac{1}{5}$3個分で$\frac{3}{5}$、、、のようになります。分数のこの意味をイメージできれば、分数のたし算やひき算などの計算方法を理解することができます。
分数の大きさは、もとの量を分母の数で等分したものの、分子の個数分になるので、
もとの量÷分母×分子
で計算できます。
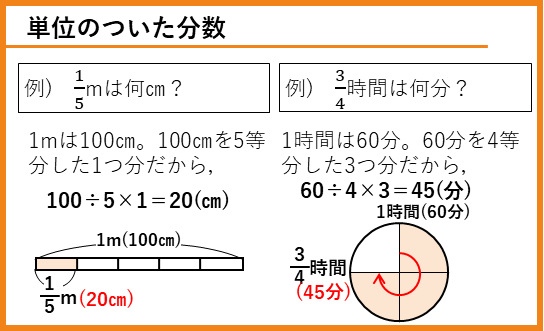
単位のついた分数
$\frac{1}{5}$mは、1mが100㎝なので、
100÷5×1=20(㎝)
で求められます。
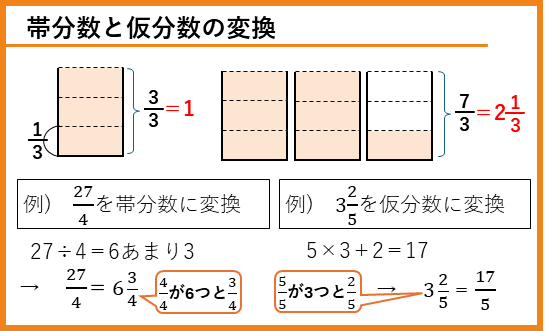
真分数・仮分数・帯分数
真分数、仮分数、帯分数という分数の表し方を覚えましょう。

帯分数と仮分数の変換
分数のたし算とひき算
$\frac{3}{7}$+$\frac{2}{7}$というたし算は、$\frac{1}{7}$が3つ分と$\frac{1}{7}$が2つ分をたし合わせるので、答えは$\frac{1}{7}$が5つ(3+2=5)分の$\frac{5}{7}$になります。このことから、分数のたし算では、分母は同じままで分子だけをたせばよいことがわかります。
分数のひき算も同じように考えられます。

帯分数のたし算とひき算
帯分数のたし算とひき算は、整数部分どうし、分数部分どうしを計算します。分数どおしのひき算ができないときは、整数部分から1をかりてきて計算します。
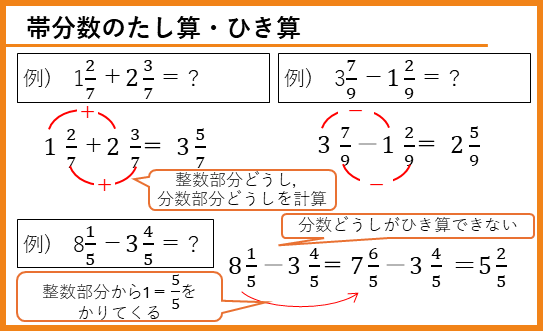
また、分数部分どうしのたし算の結果が仮分数になった場合は帯分数になおします。
練習問題
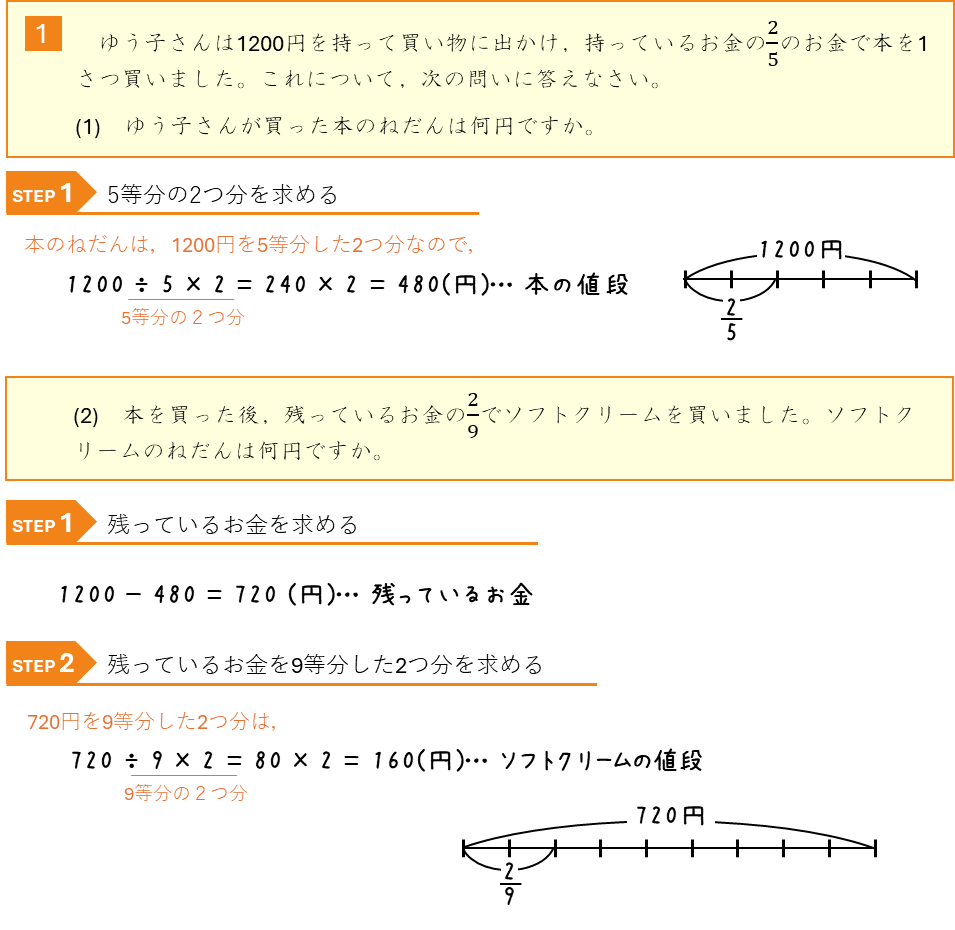
分数の計算ーもとの量の〇分の△を求める
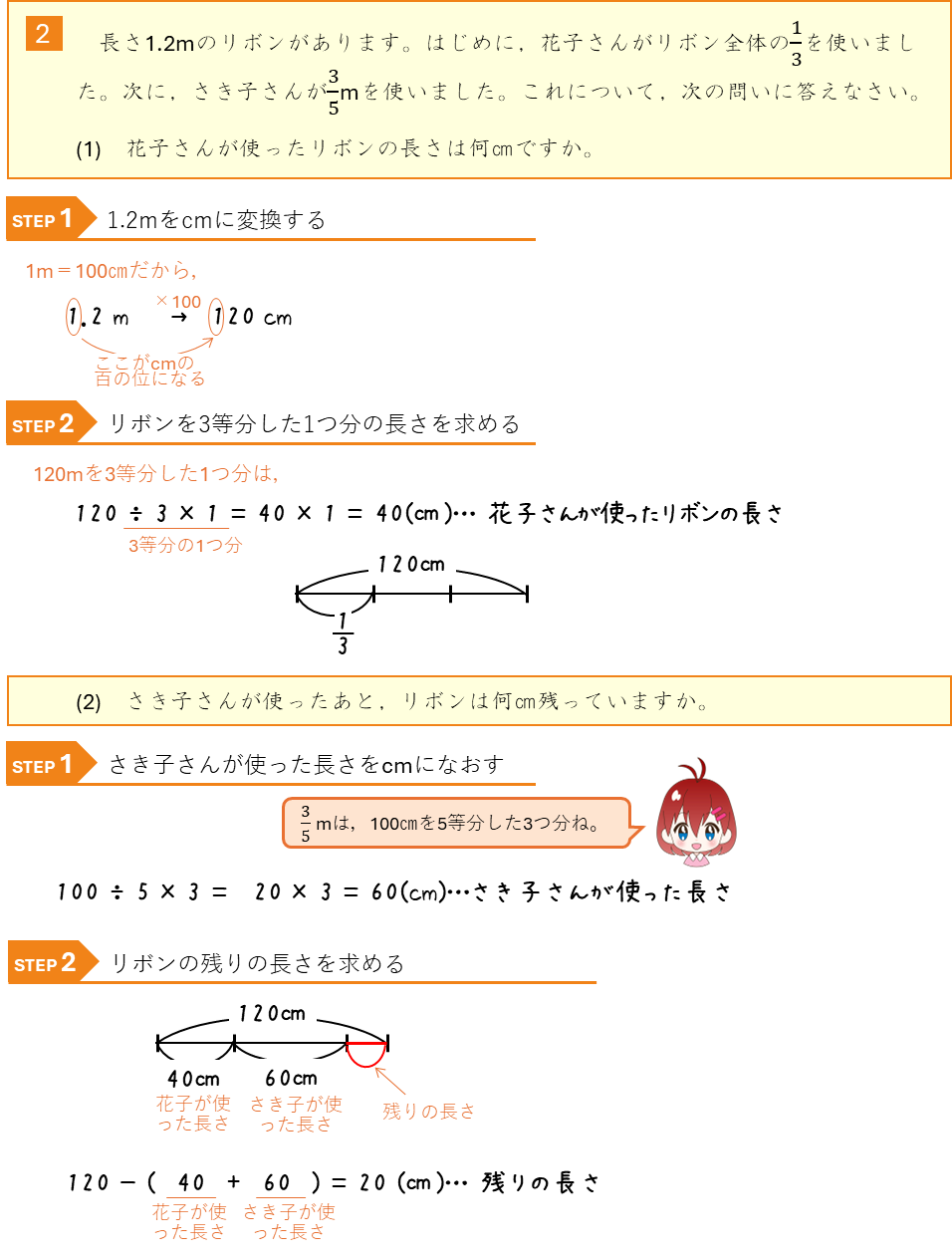
単位のついた分数の計算ー長さ
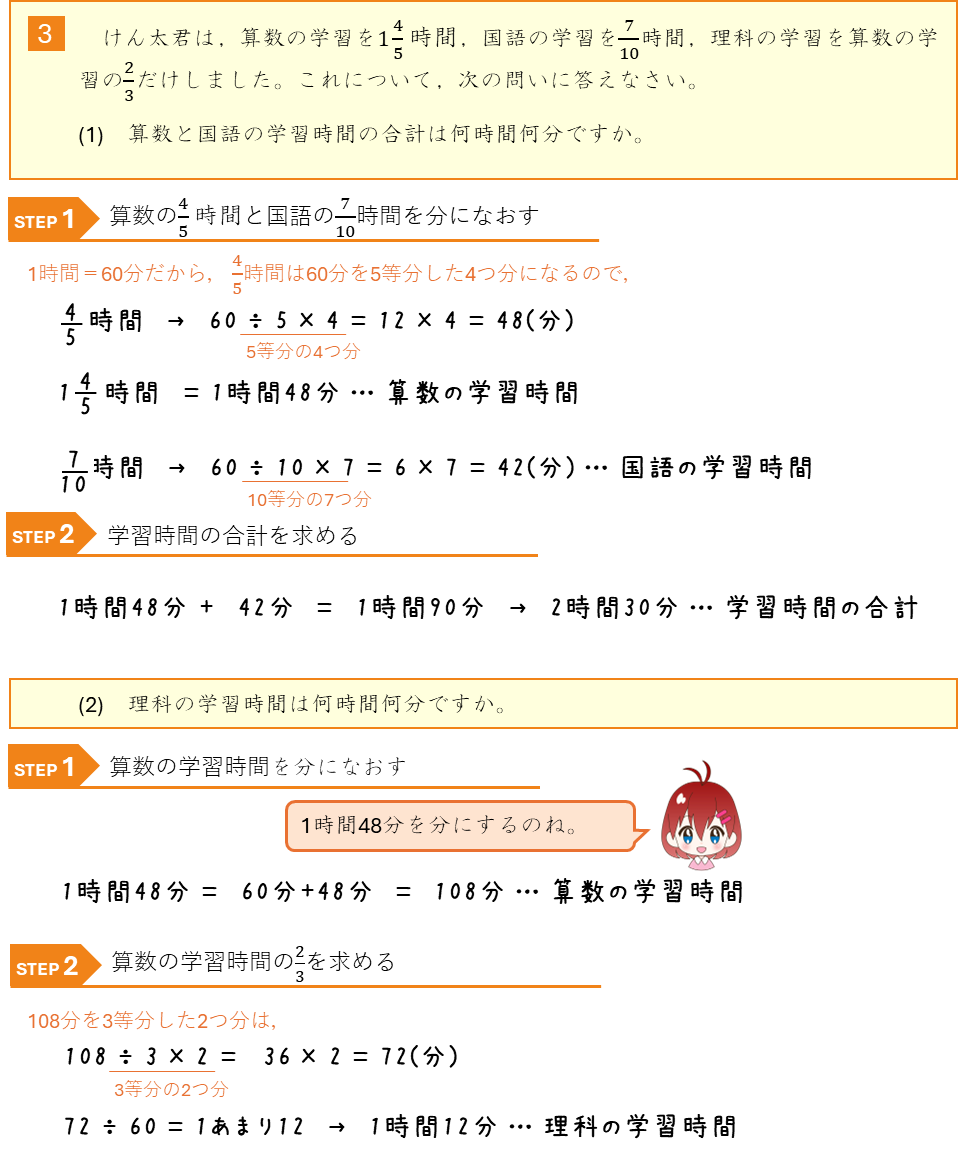
単位のついた分数の計算ー時間
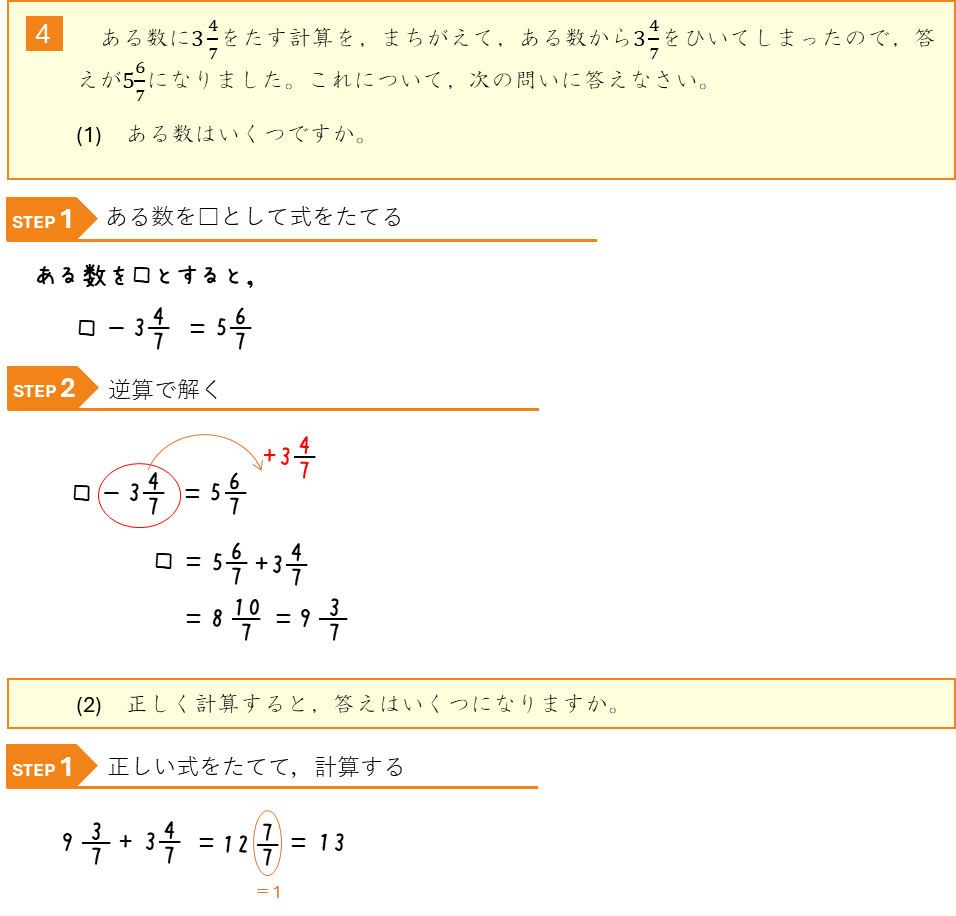
分数ー計算をまちがえた
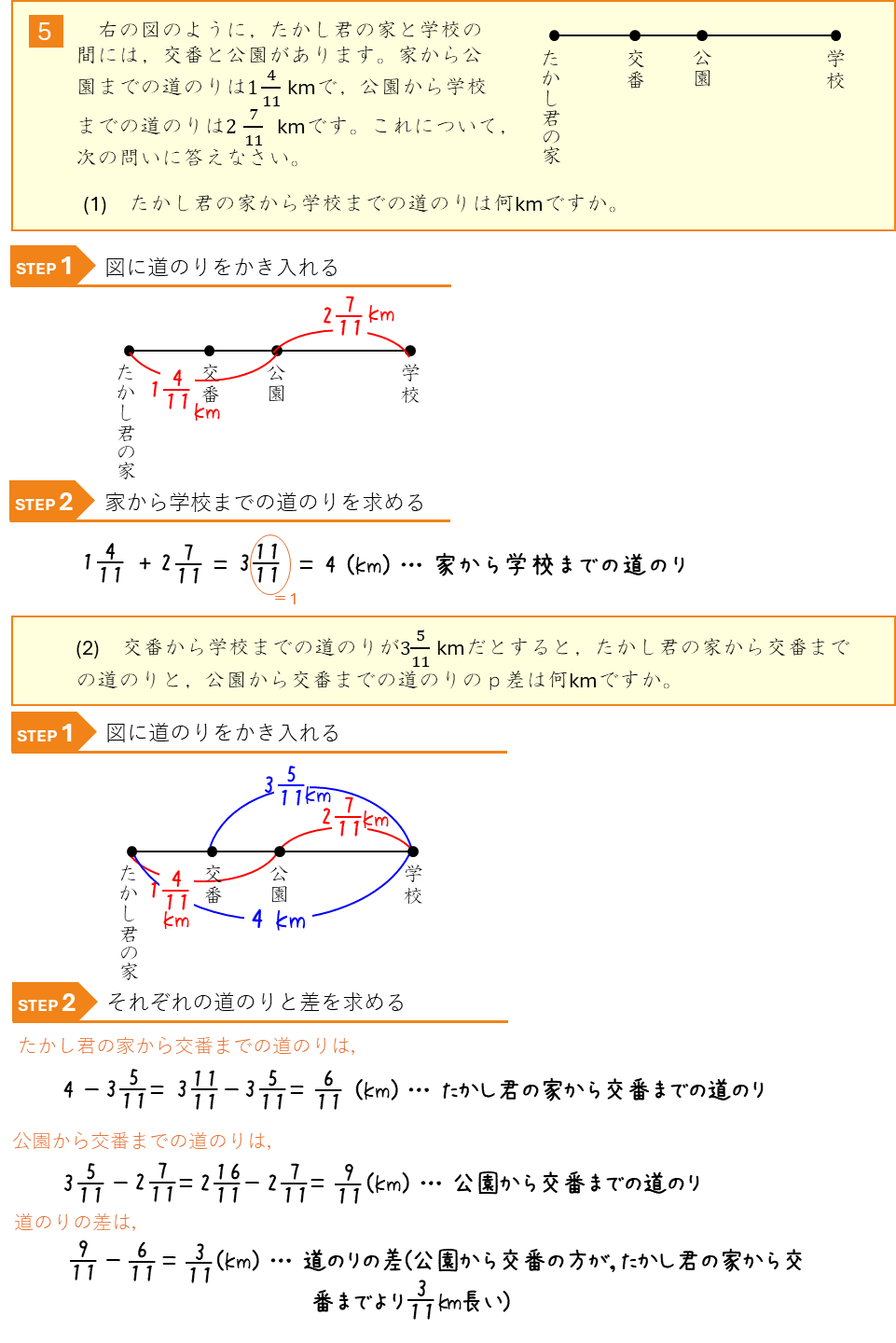
単位のついた分数の計算ー道のり

コメント