
「面積図で解こう!」の第3回目は、特殊算の平均算と濃度算の例題を解いていきます。
平均算と濃度算の面積図を使った解法も、つるかめ算と同じように3つの手順(ステップ)になります。「平均算・濃度算の面積図3ステップ解法」として覚えましょう。
面積図で解く平均算と濃度算ー3ステップ解法
前回のつるかめ算と同じように、平均算、濃度算でも2つの量があって、積の式が2つができる問題では長方形を2個つ組み合わせた面積図をかきます。ここに、さらに全体の平均の長方形、全体の濃度の3つ目の長方形を重ねて解いていきます。この面積図から、面積が等しくなる部分を見つけるのがポイントです。
平均算と濃度算の面積図による解法をまとめます。
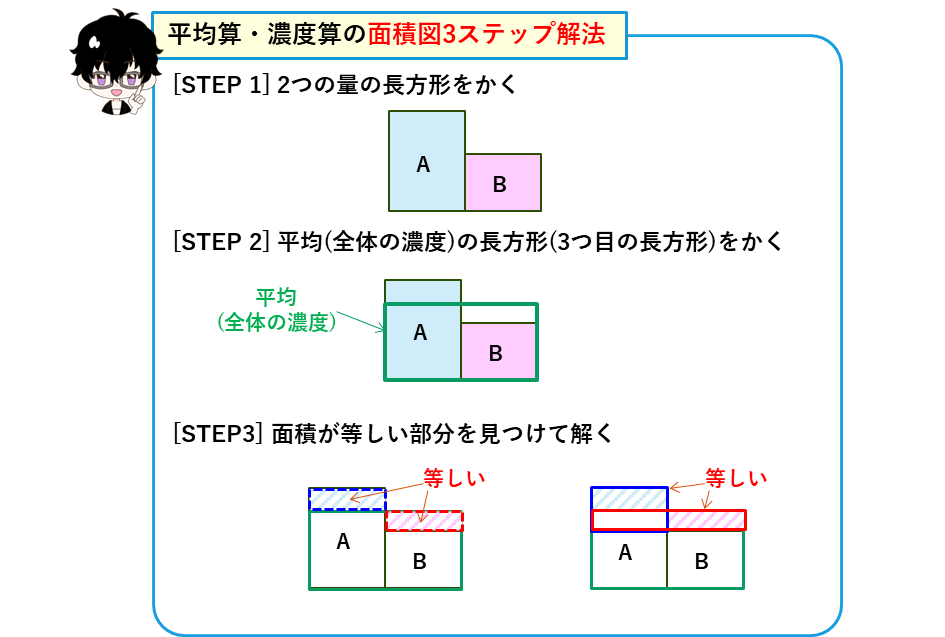
STEP 1: 2つの量の長方形をかく
STEP 2: 平均(全体の濃度)の長方形(3つ目の長方形)をかく
STEP 3: 面積が等しい部分を見つけて解く
の、3つのステップです。
この解法を使って、平均算と濃度算の例題を解いていきます。
面積図で解く平均算
人数を求める平均算
最初の平均算の例題です。

問題から、
・大人の年令の平均は30才
・子どもの年令の平均は15才
と,2つのグループの平均があります。
・大人の年令の合計=30× 大人の人数(人)
・子どもの年令の合計=15× 子どもの人数(人)
と、2つの積の式ができるので、それぞれ平均の長方形の面積図をかきます
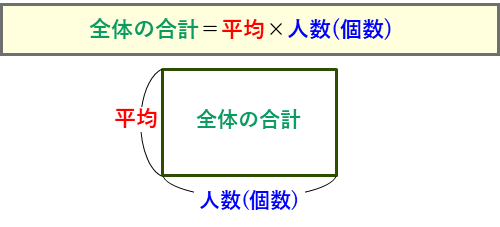
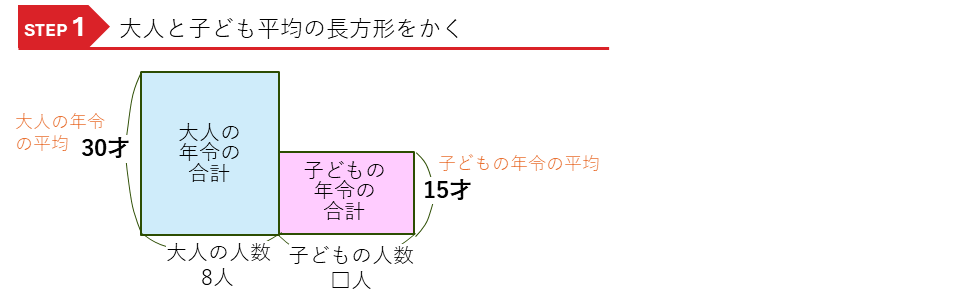
次に、この面積図に全体の平均の長方形を重ねてかき加えます。
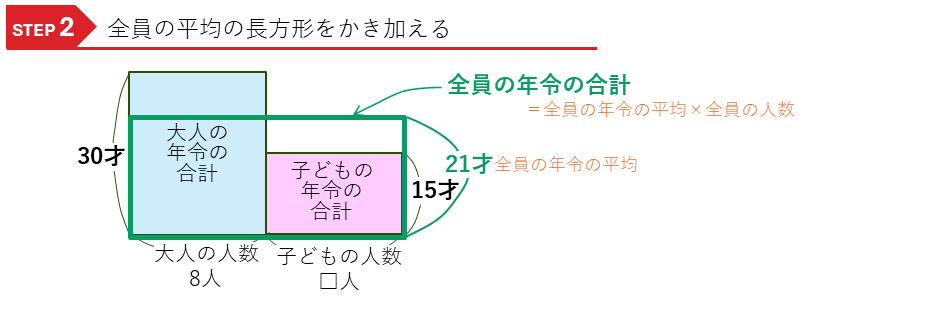
この面積図で面積が等しいところに注目して解いていきます。

まず、年令の合計は、大人の年令の合計と子どもの年令の合計で、これは、全員の年令の平均から計算した合計と等しくなります。
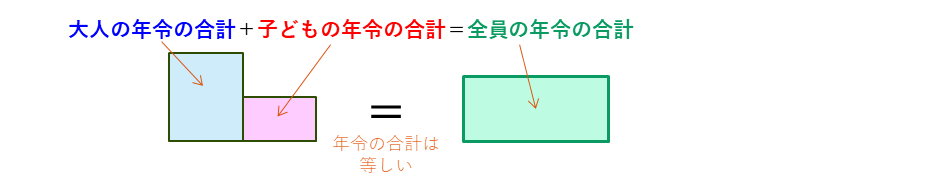
面積図では、大人の年令の長方形(青の長方形)と子どもの年令の長方形(赤の長方形)の面積の和が、全員の年令の長方形(緑の長方形)の面積と等しくなります。
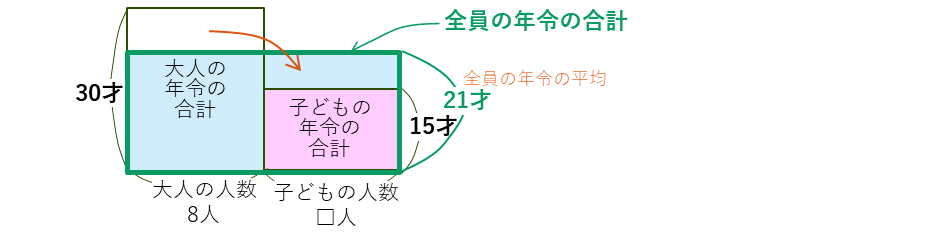
これから、大人の年令の長方形の飛び出した部分の面積、子どもの年令の上の部分にあるすき間の面積と等しいことがわかります。このことから、子どもの人数を求めます。
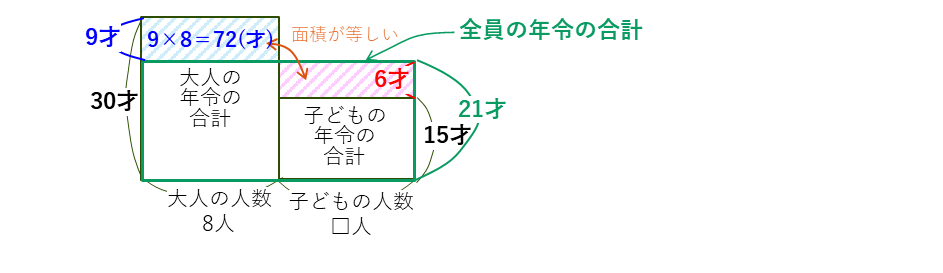
大人の年令の長方形の飛び出した部分の面積は、
9×8=72(才)
で、子どもの年令の上の部分の面積も72(才)となることから、
72÷6=12(人)…子どもの人数
から、子どもに人数が求まります。
合格者の平均点
平均算の次の問題では、2つのグループ(合格者と不合格者)の人数と全体の平均が分かっていて、それぞれの平均を求めるものです。

問題から、
・合格者の人数が180人、平均点は不明
・不合格者の人数が420人、平均点は不明
となっています。2つのグループがあります。
・合格者の点数の合計=合格者の平均点× 180(人)
・不合格者の点数の合計=不合格者の平均点×420(人)
と、2つの積の式ができるので、それぞれ平均の長方形の面積図をかきます。
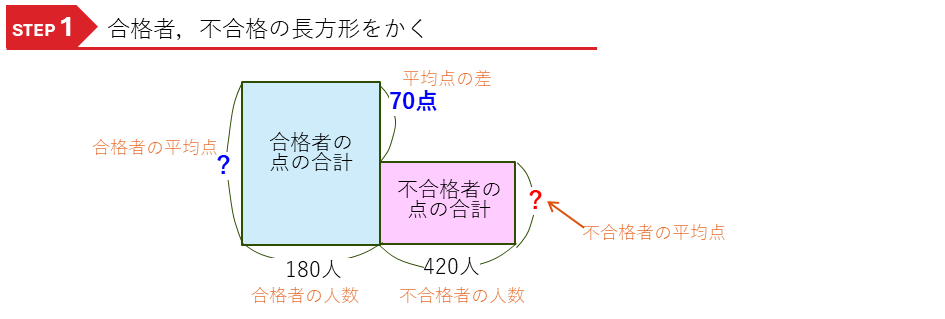
ここに、3つ目の長方形として、受験者全員の点数の合計の長方形をかき加えます。
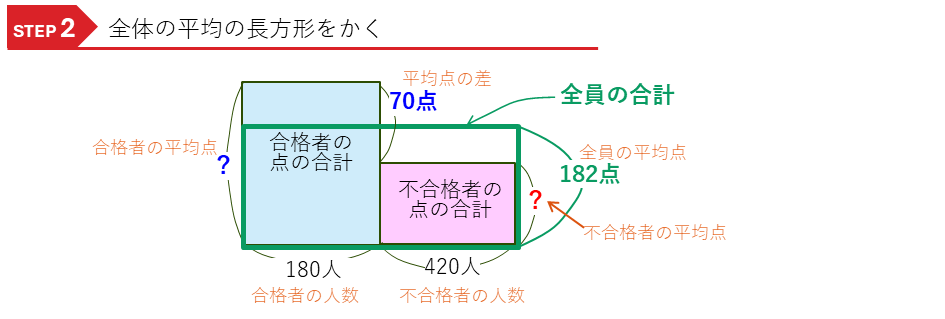
最後に、面積が等しいところに注目して、合格者の平均を求めます。

前の問題と同じように、全体の平均から飛び出した合格者の点数(でこ)と、全体の平均に届いていない不合格者の点数(ぼこ)が等しくなりますが、それぞれの平均点が分からないので、面積を求めることができません。そこで共通な部分を加えた長方形で考えます。

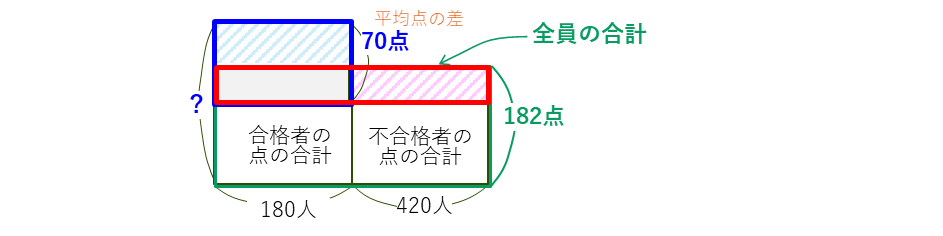
青の長方形は、たての値も横の値も分かっているので、面積が求まります。これが赤の長方形の面積と等しくなることから、

赤の長方形のたてが、21(人)と分かるので、
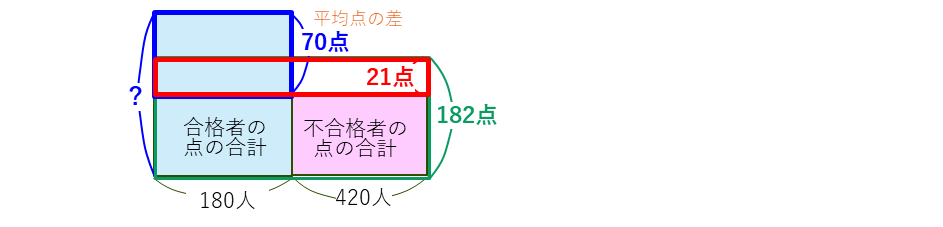
不合格者の平均点は、
182-21=161(点)…不合格者の平均点
となり、合格者の平均点は、
161+70=231(点)…合格者の平均点
となります。
面積図で解く濃度算
次に、濃度算の問題を解いてみます。濃度算は、異なる濃度の食塩水を混ぜ合わせる問題です。2種類の食塩水を混ぜる問題では、それらの食塩水の2つ積の式と混ぜ合わせた後の全体の食塩水の積の式ができるので、その長方形をかいて考えます。
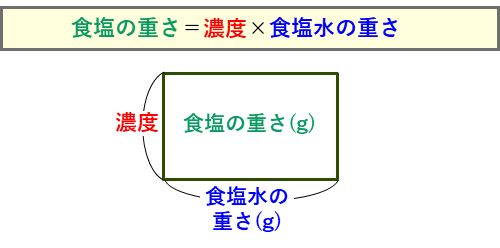
濃度算ーもう一方の食塩水の重さを求める
次の問題は、
・5%の食塩水
・20%の食塩水
と,2種類の濃度の食塩水があります。

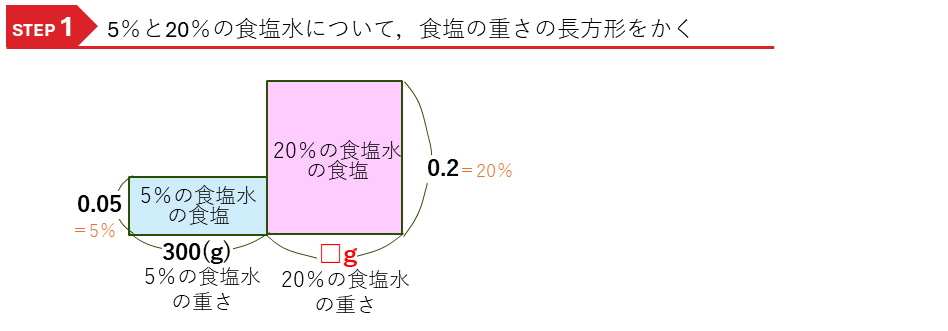
・5%の食塩水の食塩の重さ(g) =0.05× 5%の食塩水の重さ(g)
・20%の食塩水の食塩の重さ(g) =0.2× 20%の食塩水の重さ(g)
という2つの積の式ができるので,それぞれの長方形をかきます。
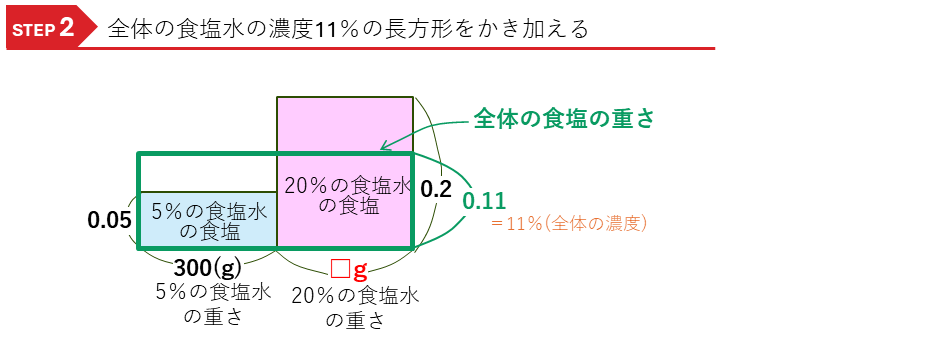
ここに、全体の食塩水の長方形をかき加えます。
最後に、面積が等しいところに注目して、20%の食塩水の重さを求めます。

全体の食塩の重さは、5%の食塩水の食塩と20%の食塩水の食塩の合計であり、全体の食塩水の濃度から計算した全体の食塩の重さと等しくなります。

面積図では、5%の食塩水の食塩の長方形(青の長方形)と20%の食塩水の食塩の長方形(赤の長方形)の面積の和が、全体の食塩水の濃度から計算した全体の食塩の重さの長方形(緑の長方形)の面積と等しくなります。
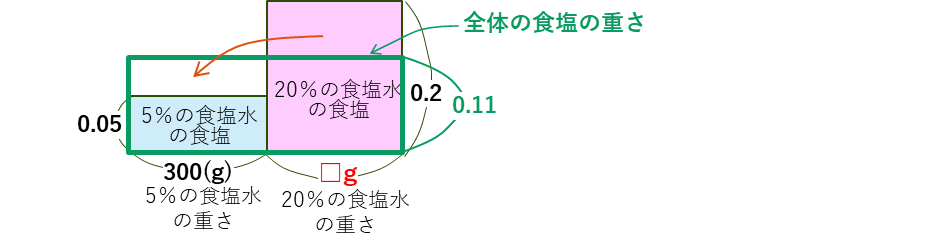
これから、5%の食塩水の食塩の上にあるすき間の面積と20%の食塩水の食塩の飛び出した部分の面積が等しいことがわかります。これから、20%の食塩水の重さを求めます。
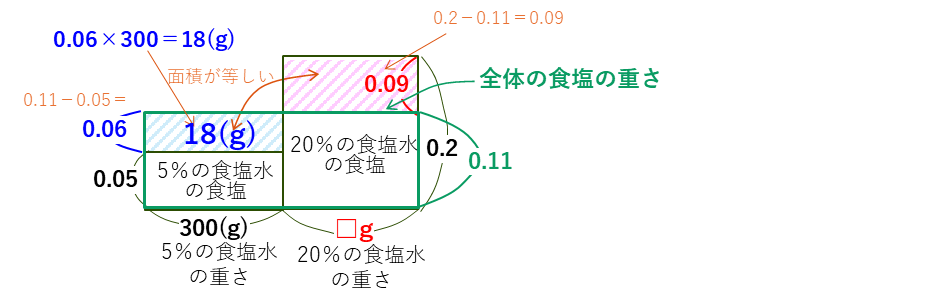
5%の食塩水の上のすき間の面積(青の長方形)は、
0.06×300=18(g)
で、これは、20%の食塩水の飛び出た部分の面積(赤の長方形)と等しくなります。したがって、
18÷0.09=200(g)…20%の食塩水の重さ
から、20%の食塩水の重さが求まります。
濃度算ー全体の重さからそれぞれの食塩水の重さを求める
次の、濃度算の問題は、全体の食塩水の重さが分かっていて、それぞれの食塩水の重さを求めるものです。

・15%の食塩水
・6%の食塩水
と、前の問題と同じように2種類の濃度の食塩水があります。2種類の食塩の積の式できるので,それぞれの長方形をかきます。
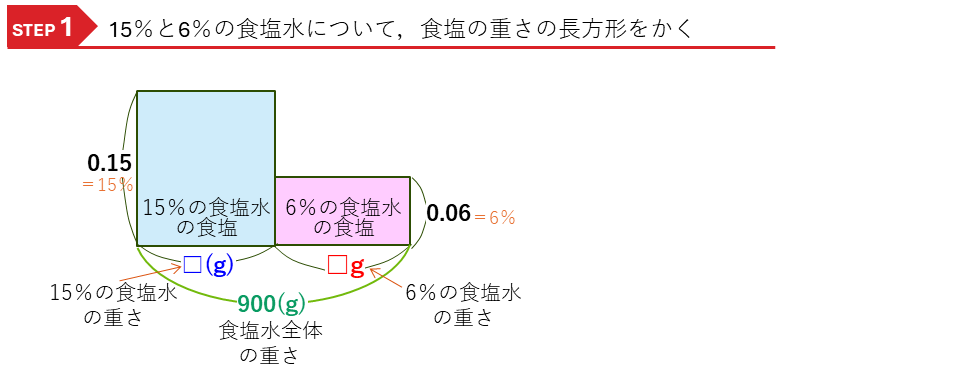
ここに、全体の食塩水の長方形をかき入れます。
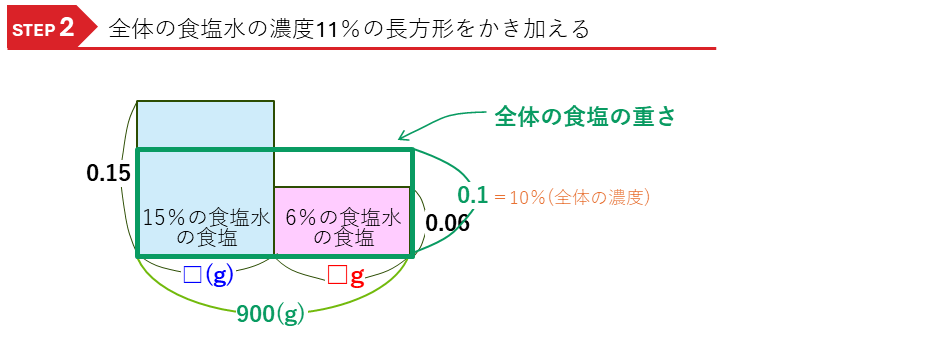
面積が等しいところに注目して、15%の食塩水の重さを求めます。

前の問題と同じように、全体の食塩水の長方形から飛び出した食塩の重さ(でこ)と、全体の食塩水の長方形の中のすき間の食塩水の重さ(ぼこ)が等しくなりますが、それぞれの食塩水の重さが分からないので、面積を求めることができません。

そこで共通な部分を加えた長方形で考えます。

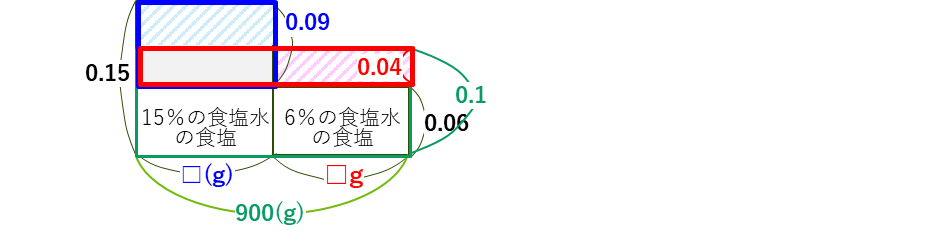

赤の長方形は、たての値も横の値も分かっているので、面積が求まります。
0.04×900=36(g)
これが青の長方形の面積と等しくなることから、
36÷0.09=400(g)…15%の食塩水の重さ
となります。
平均算と濃度算の面積図による解き方を解説しました。濃度算では、全体の食塩水の濃度は、2つの食塩の濃度の平均になるので、平均算と同じように解くことが理解できたかと思います。
平均算と濃度算の面積図による解法ば冒頭の説明の通り、

の、3つのステップです。この手順を身に付けて、いろいろな例題に取り組んでいきましょう。
コメント