
今回が「線分図を攻略するシリーズ」の最終回です。線分図で解く特殊算の3回目になります。「ニュートン算(5年下)」と「差集め算(過不足算)(4年夏期講習)」です。どちらも「わり算の線分図」で解いていきます。
また、特殊算ではありませんが、同じく「かけ算・わり算の線分図」で表す等差数列にも解説します。
線分図で解く特殊算ーニュートン算・差集め算(過不足算)
ニュートン算
ニュートン算は,
・水がわき出る泉の水をポンプでくみ出す
・穴があいた水そうに水を入れる
・毎日はえてくる牧草を牛が食べる
・行列に次々ならぶ人を入場口から中に入れる
など,増えていくのと減っていくのが同時におこることを考える問題です。
ニュートン算ーポンプが毎分くみ出す水の量を求める

このニュートン算の問題では、ポンプ1台で毎分くみ出す水の量(出ていく量)を求める問題です。ニュートン算では、
はじめの量 + 入ってくる量の合計 = 出ていく量の合計
の関係を線分図にかきます。
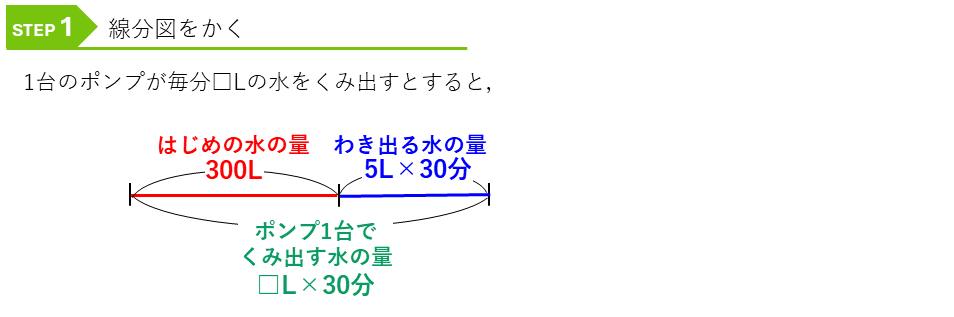
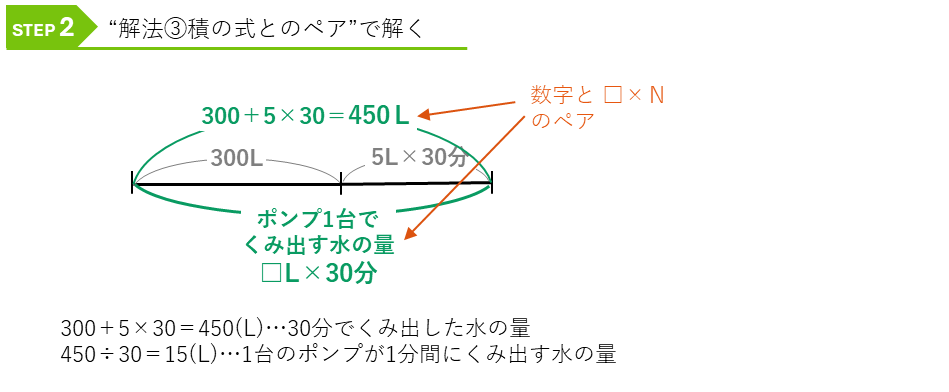
はじめの水の量と30分間でわき出る水の量は、300+5×30=450(L)と求めることができます。ここで解法③積の式とのペアから、解いていきます。

ニュートン算ー泉が空になるまでの時間を求める
次のニュートン算の問題は、泉が空になるまでの時間を求める問題です。線分図をかいて考えます。

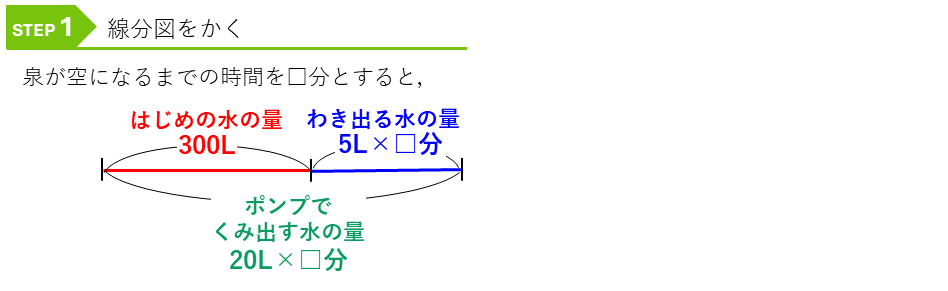
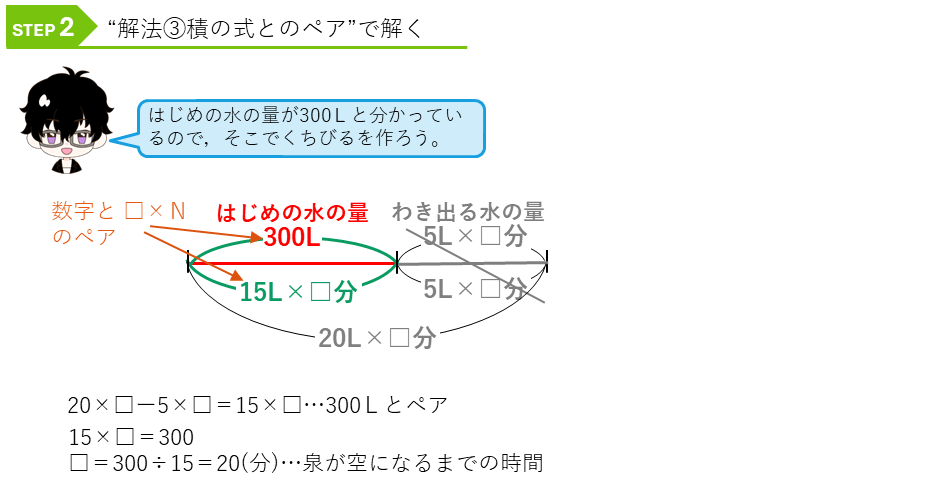
はじめの水の量が300Lと分かっているので、この部分で「数と積の式(N×□)のペア」を作れないか考えてみます。

ニュートン算ー2つの場合があってはじめの量が分からない

このニュートン算の問題では、はじめの量が不明です。毎分10Lくみ出すと空になるまで60分、毎分15Lでくみ出すと空になるまで30分という2つの場合があります。このような問題では、それぞれの場合を線分にする線分図をかいて、その差を考えていきます。
ここでのポイントは、「年令算」であったのと同じように、同じ量は必ず左側にそろえてかくことです。


2つの条件の差に着目します。差の部分に数と積の式(□×N)のペアを見つけて,□を求めます。

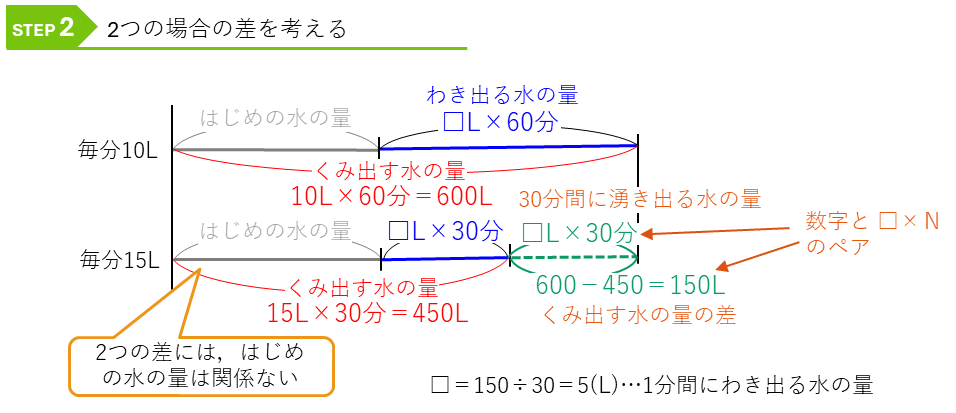
このように「2つの場合があってはじめの量が分からない」ニュートン算の問題では,差の線分図をかいて考えましょう。はじめの量を左にそろえてかくと、はじめの量は差には関係ないことがよく分かるようになります。
差集め算(過不足算)
差集め算は,1個あたりの差が集まって全体の差になるという考え方を使って解く問題です。また,あまりや不足が出る問題では,あまりと不足の差が全体の差になるということから過不足算とも言います。差集め算(過不足算)は,差の線分図をかいて解くことができます。

3まいずつ配る場合と7まいずつ配る場合の枚数を表す線分図をかきます。
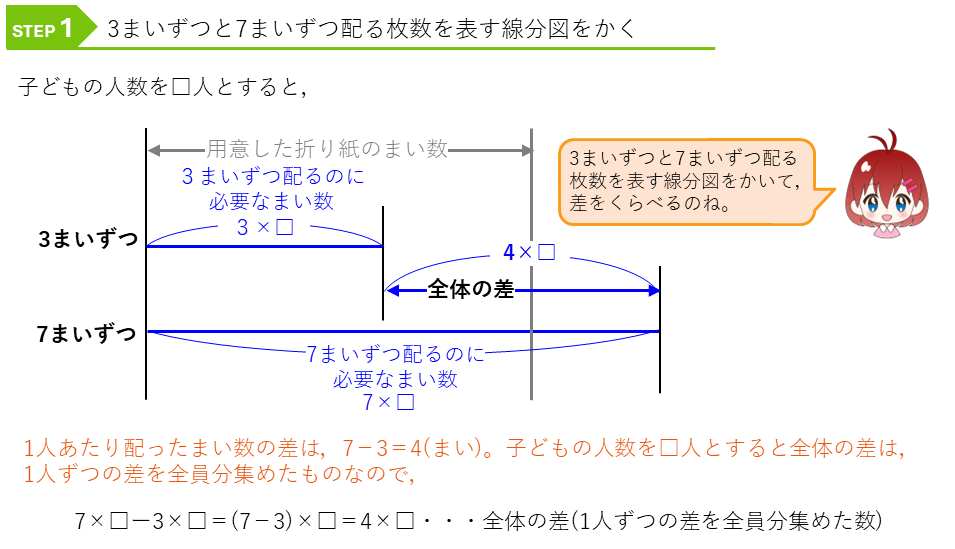
次に、あまりと不足をこの線分図にかき加えます。あまりと不足の差も全体の差になるので、差の数と積の式のペアができます。

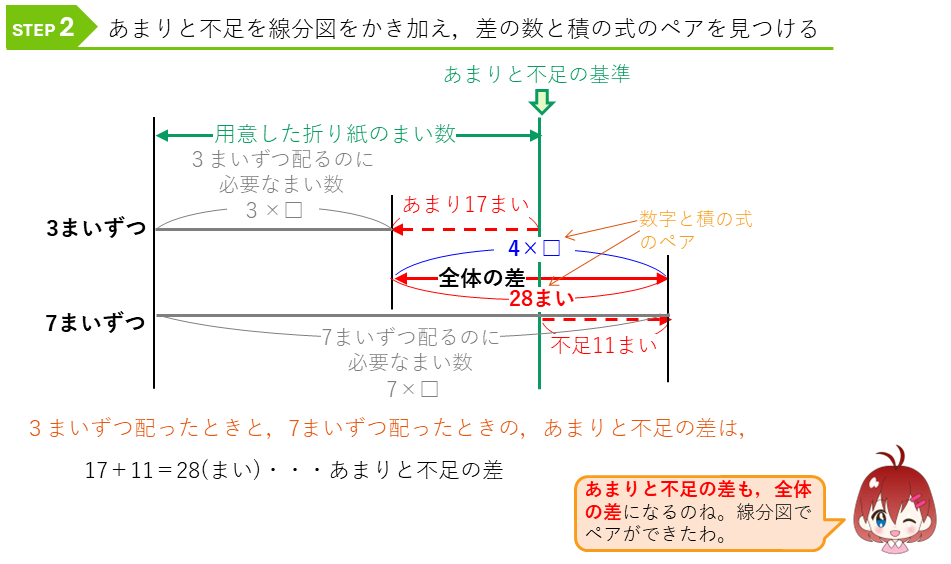

線分図を使うほかの問題
ここまでで説明した特殊算の他に、線分図はいろいろなところで使われます。
等差数列

等差数列の公式

を覚えていれば解けますが、ちゃんと意味を理解しておきましょう。等差数列は、次のような積の線分図で表すことができます。
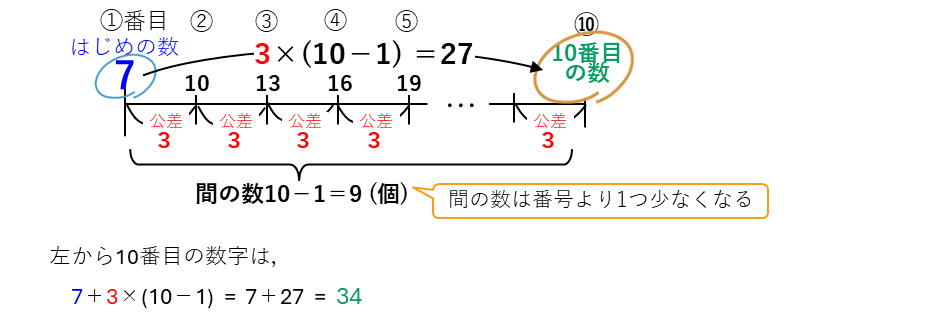
このイメージを身につけることができれば、公式を思い出すことができます。

これで、線分図の解説は終わりです。説明を全部読むのは大変だったと思いますが、それだけ線分図はいろいろな問題で使われていることが分かったと思います。

問題を読んで線分図をかくのが、やっぱり難しいなぁ

はじめはそうかもしれないね。いろいろな問題を解いて、線分図をかけるようになろうね。線分図が正しくかければ、解法は多くないので解けると思うよ。

はい。これから頑張ります!
コメント