
線分図で解く特殊算の2回目です。今回は、5年生で学習する「相当算(5年上)」、「年令算(5年下)」、「倍数算(5年下)」、「旅人算(5年上、5年下)」です。割合・比を使う特殊算を、線分図をかくことで具体的なイメージを持って解くことができます。
線分図で解く特殊算ー相当算・年令算・倍数算・旅人算
相当算
相当算は、割合のもとにする量(1にあたる(相当する)量)を求める問題です。
相当算ー差の量が分かる

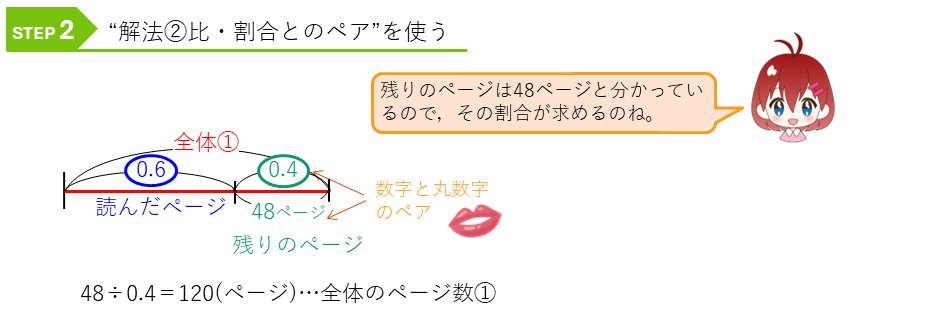
全体のページを①として線分図をかきます。

実際の数と割合を表す丸数字のペアを見つけて解きます。

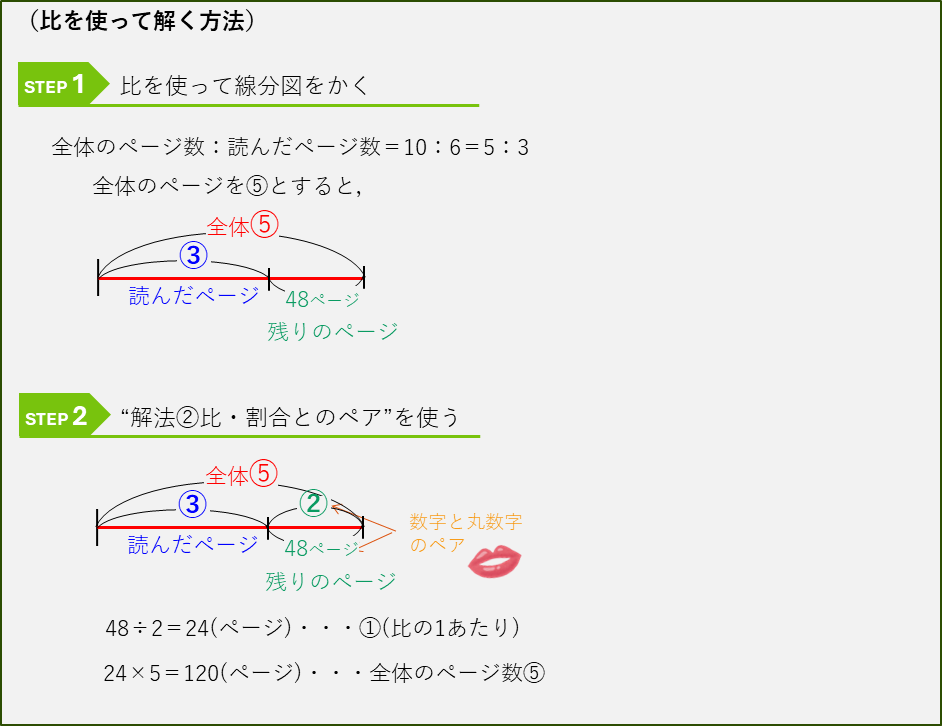
全体のページ数と読んだページ数の比を使って解くこともできます。整数で考えることができるので、分かりやすいです。
相当算ーはんぱな量がある

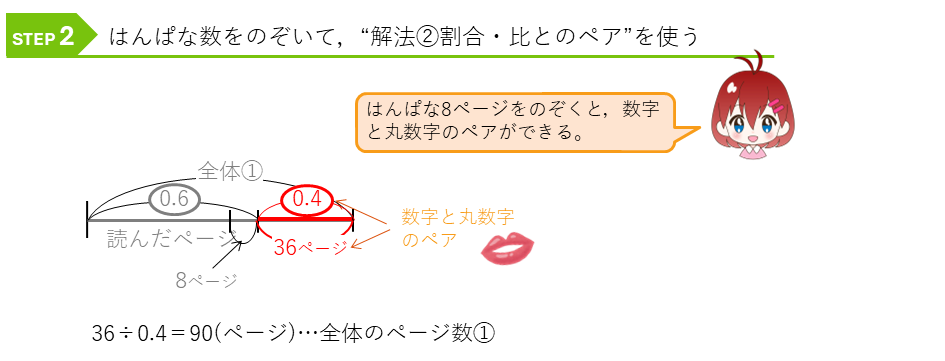
全体を①として、線分図をかきます。

ぱんぱなページをのぞいて、割合・比の解法を使います。

相当算の応用問題では,はじめに読んだ残りをさらに何割か読むという2段階の問題があります。少し複雑になりますが,同じように線分図をかいて「数字と丸数字のペア」を見つけて解くことができます。
年令算
年令算は、年令に関する特殊算です。「だれでも同じだけ年をとる」ので、何年前でも何年後でも「年令の差は一定」という条件を使うことが多いです。
年令算ー何年後に年令がX倍?
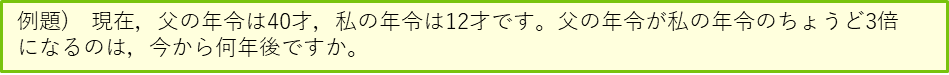
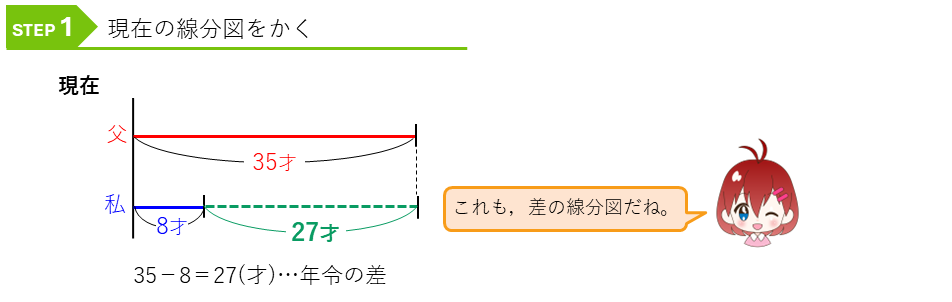
まずは、現在の線分図をかいてみます。
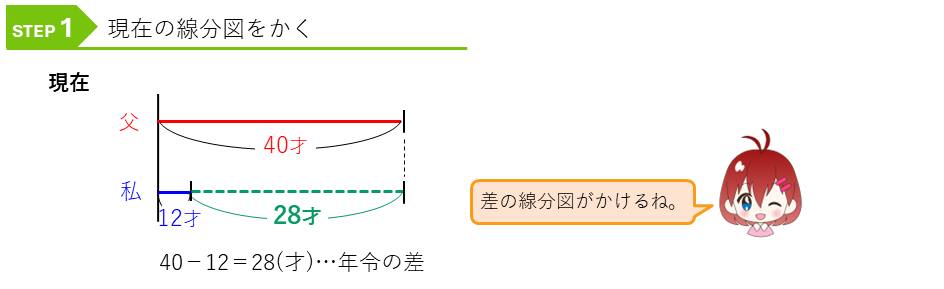
次に、この現在を表す線分図から、「父の年令が私の年令のちょうど3倍になる」ときの線分図にかきかえてみます。
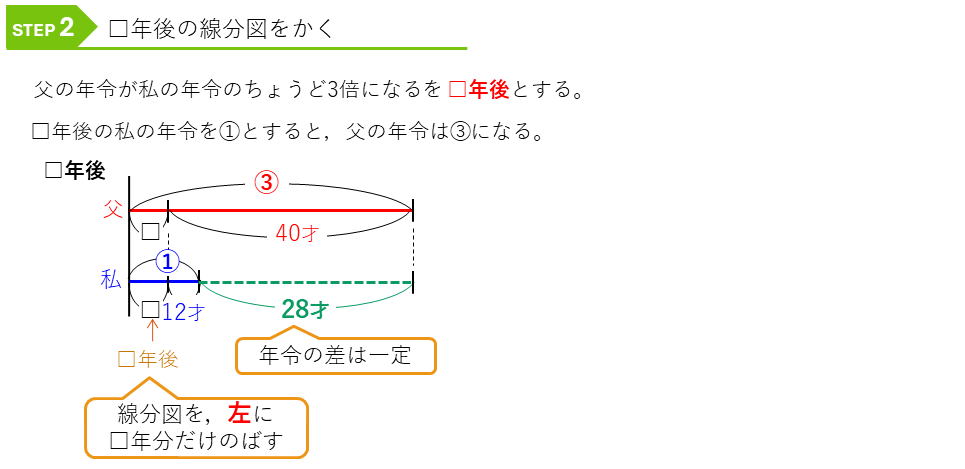
ここでのポイントは、□年後は左にそろえてかき入れることです。同じ量は左にそろえてかくことは線分図の鉄則ですので、しっかり覚えておきましょう。

これによって、父と私の年令の差は(40ー28=)12(才)ということが簡単にわかります。
これで線分図はかけたので、割合・比とのペアの解法を使って解きます。

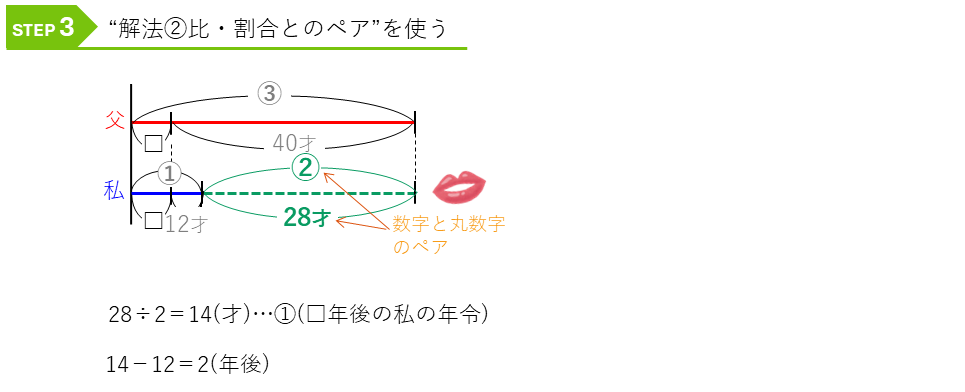
これで回答がえられましたが、STEP 2で、右に線分図をのばしてしまったらどうなるのか、ちょっと考えてみましょう。
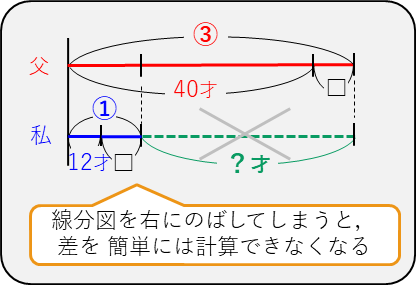
上の図のように、右にのばしてしまうと、図の差の中に”□”が入ってしまいます。

と解けるのですが、線分図を見てもわかりづらく、線分図でかいた効果が激減してしまいます。左側にのばせば線分図から、差が「40-28」であることが一目りょうぜんですので、「同じ量は左側にそろえてかく」という鉄則を覚えておきましょう。
年令算ー何年前に年令がX倍?
次は、何年か前に年令が何倍だったという問題です。

まずは、現在の線分図をかいてみましょう。
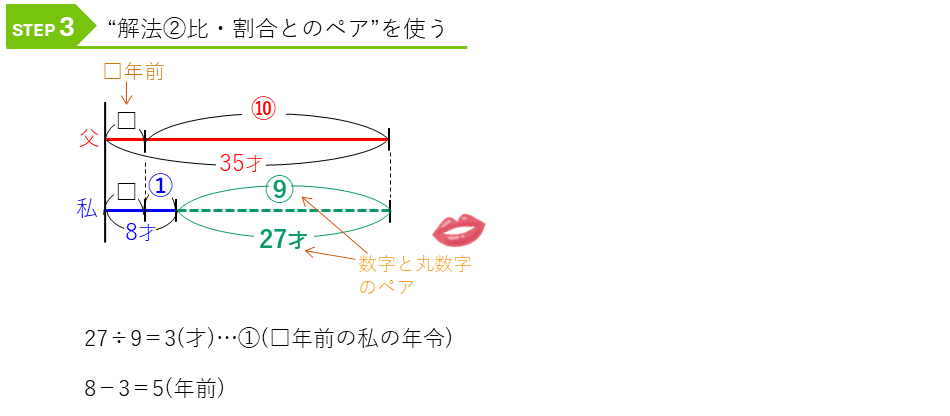
次に、この現在を表す線分図から、□年前に「父の年令が私の年令のちょうど10倍だった」として、線分図にかきかえてみます。

ここでも、「同じ量は左側にそろえてかく」という鉄則を守ってかきます。

さあ、割合・比とのペアの解法を使って解きましょう。

倍数算
倍数算は、「やりとりなどによって、やりとり前とやりとり後で比が変化する問題」です。やりとりする前と後で変わらない量が、2つ比でことなる数で表されているときは、それを最小公倍数にそろえて解きます。
倍数算ー2人の合計が変わらない

まず、やりとり前の比を線分図にかきます。

この問題では、兄が弟にカードを10枚あげたので、2人の持っているカードの合計は変わらないことがわかります。やりとり前後で2人の合計が変わらないように、線分図にやりとり後の比をかき加えます。
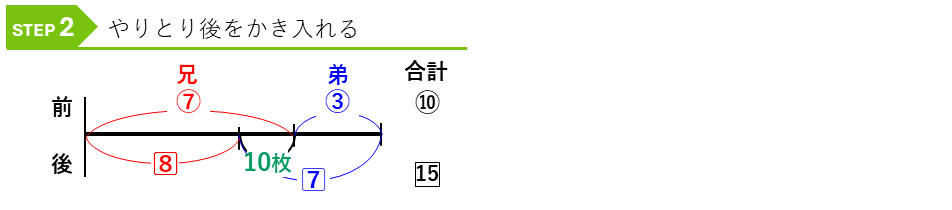
やりとり前後で、兄の枚数が減り、その分弟の枚数が増えたのがちょうど10枚です。
2つの比で2人の合計は、ことなる数になっている(10と15)ので、連比作るときと同じように、これを最小公倍数である30にそろえます。
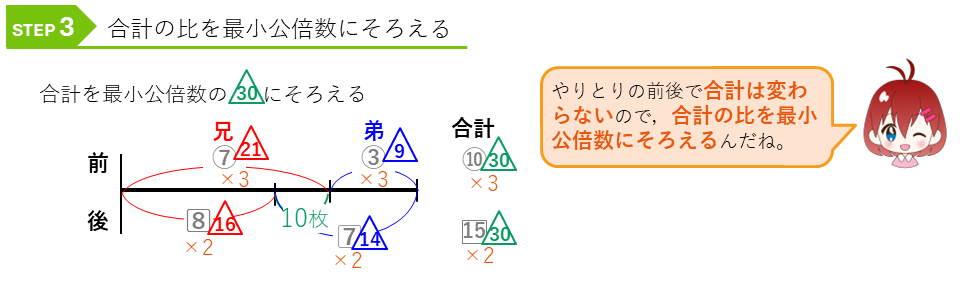
最後に、割合・比の線分図の解法を使って解きます。

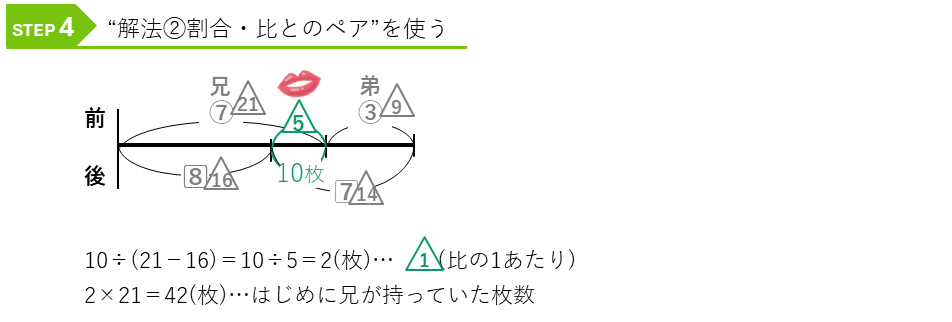
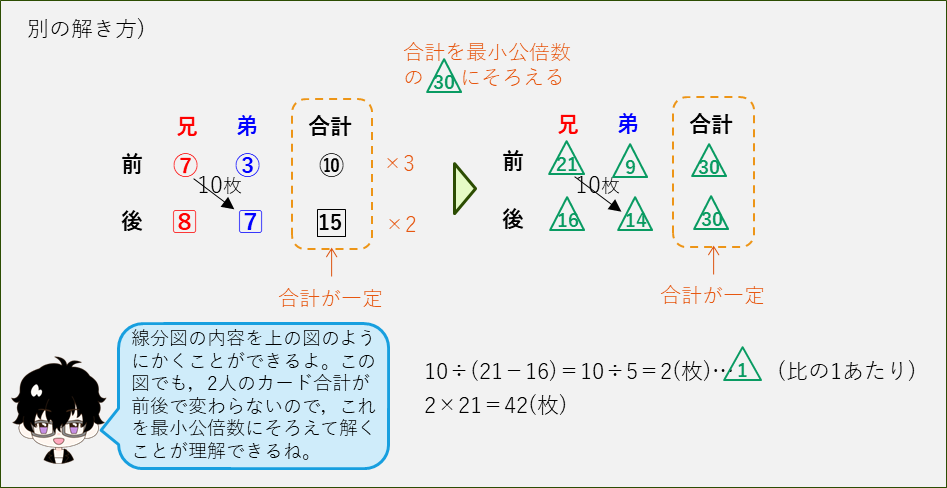
倍数算の線分図の解法を説明しましたが、線分図をかかないで次のような図で解くこともできます。この方が、図も簡単でわかりやすいと思うので理解して、解き方として覚えましょう。
旅人算
旅人算は、「2人が同じ道を進むとき、すれちがうまでの時間や追いこすまでの時間を求めたりする問題」です。
旅人算ー2人が反対方向に進む

A地点とB地点の道のりを表す線分図をかきます。
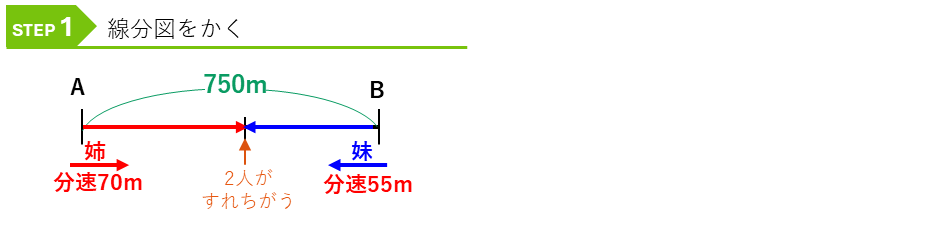
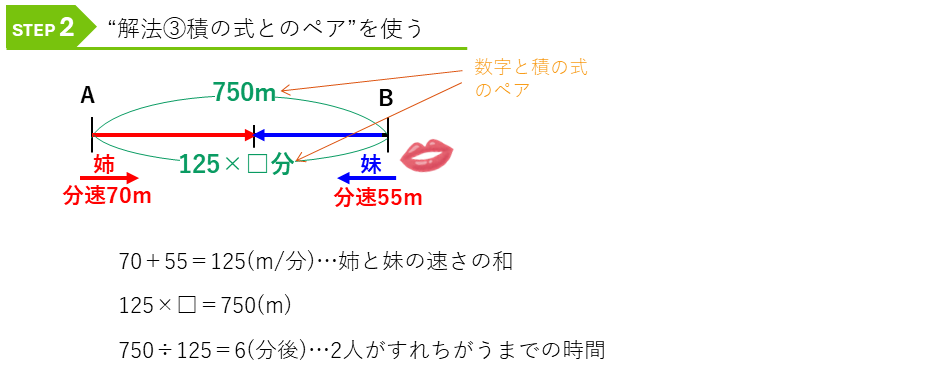
2人で750m進むまでの時間を求めることになり、2人の速さの和、つまり、毎分(70+55=)125mの速さで2人は近づきます。2人がすれちがうまでの時間を□分とすると、進んだ距離は、(125×□)mです。この積の式と実際の道のり750mのペアを作ることができます。

旅人算ー2人が反対方向に進む(速さの比)
次の例は、2人の速さの比がわかっている問題です。

線分図をかくと、
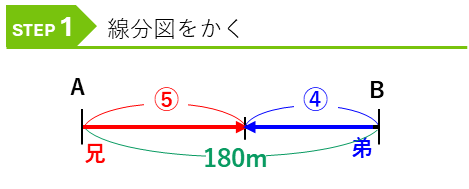
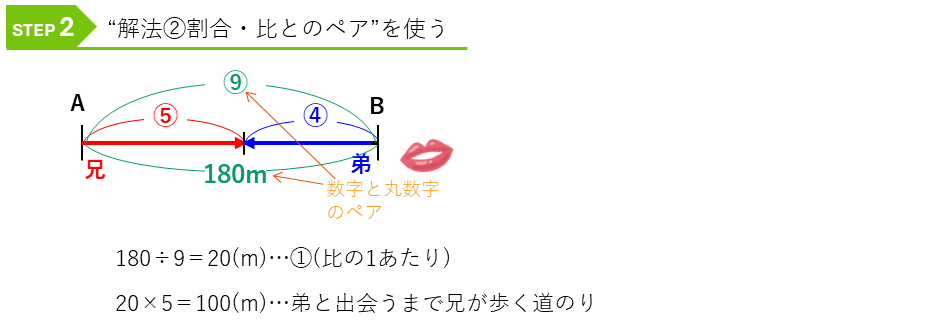
となり、実際の数字と比のペアを見つけて解きます。

旅人算ー2人が同じ方向に進む(速さの比)
同じ方向に進む場合の問題です。

P地点、Q地点と2人が出会うまでの道のりを示す線分図をかきます。姉の進んだ道のりと妹の進んだ道のりを分けた「差の線分図」をかくと分かりやすいです。
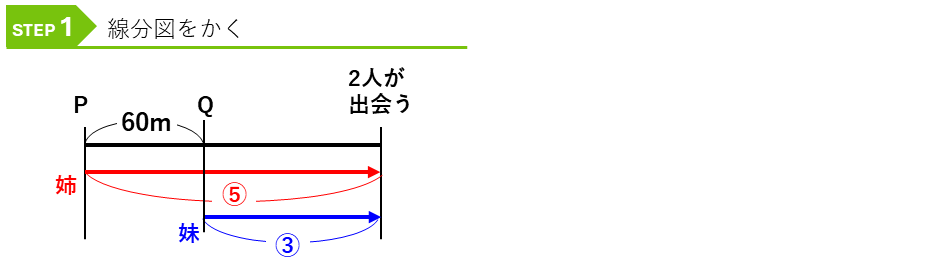
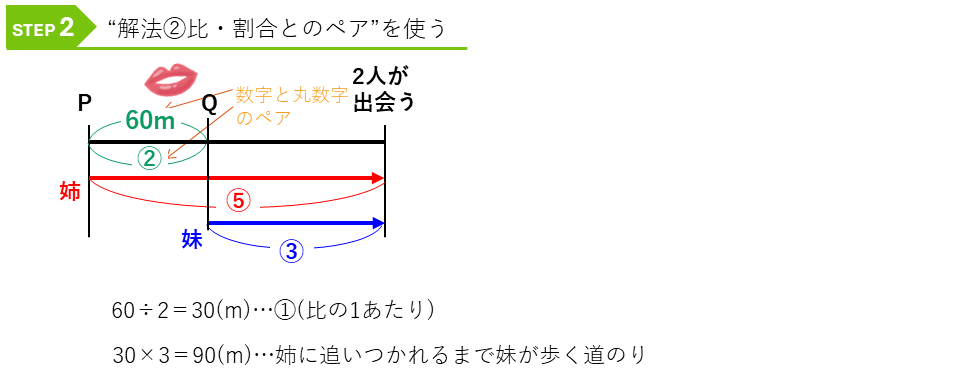
差に注目して、”解法②割合・比とのペア”で解いていきます。


5年生で習う特殊算を線分で解いてみたよ。割合と比に関する問題だったので、難しかったかな。

「数字と割合・比の丸数字のペア」を見つける解法はたくさん出てきたわ。それが大切なポイントなんだね。ただ、問題から線分図をかくところが難しいかな。。

いろいろな問題をやってみて、線分図をかけるようになろうね。
コメント