前回は、逆算のルールと公式を説明しました。逆算は、公式を使えば解くことができます。公式を簡単な例を考えて覚えたり，線分図や面積図を使って理解することができます。しかし，実際に問題を解くときに，いちいち、公式を確認している時間はありませんし，思考が途切れてしまってわけが分からなくなってしまいます。
そこで、今回は、公式を考えないでも一瞬で問題を解き進めることができて、難しい問題にも対応できる逆算の解き方を教えます。記憶に残りやすいように物語風にしてみたので、ぜひ読んでみてください。
逆算の解き方の決定版ーミスターXの正体をあばけ！
今回のきみのミッションは次の通りです。
数式で、“ミスターX□”と一緒にいるのが“仲間”です。＝の反対側を“ろうや”と考えます。仲間をつかまえてろうやにいれて、最後にミスターXの正体、つまり□の値を求めてください。例で示すと、
ミスターXの正体をあばくために、きみは2つの能力を持っています。
能力その①－ミスターXの仲間をみつけたら，ひっくり返して，ろうやにいれる
ミスターXの仲間をつかまえたら、柔道の技で「エィッ！」て投げ飛ばす（ひっくり返す）イメージがいいです。逆算では、+と－、×と÷がひっくり返ることになります。 そして、＝の向こうの”ろうや”へと放り込んでください。
ただし、この能力を使えるのは、ミスターXと仲間がたしざん”＋”か、かけ算”×”の関係、あるいは、ミスターXの後に”ー”、”÷”がある（”□ー”か、”□÷”）のときです。
逆算の公式にあてはめると、
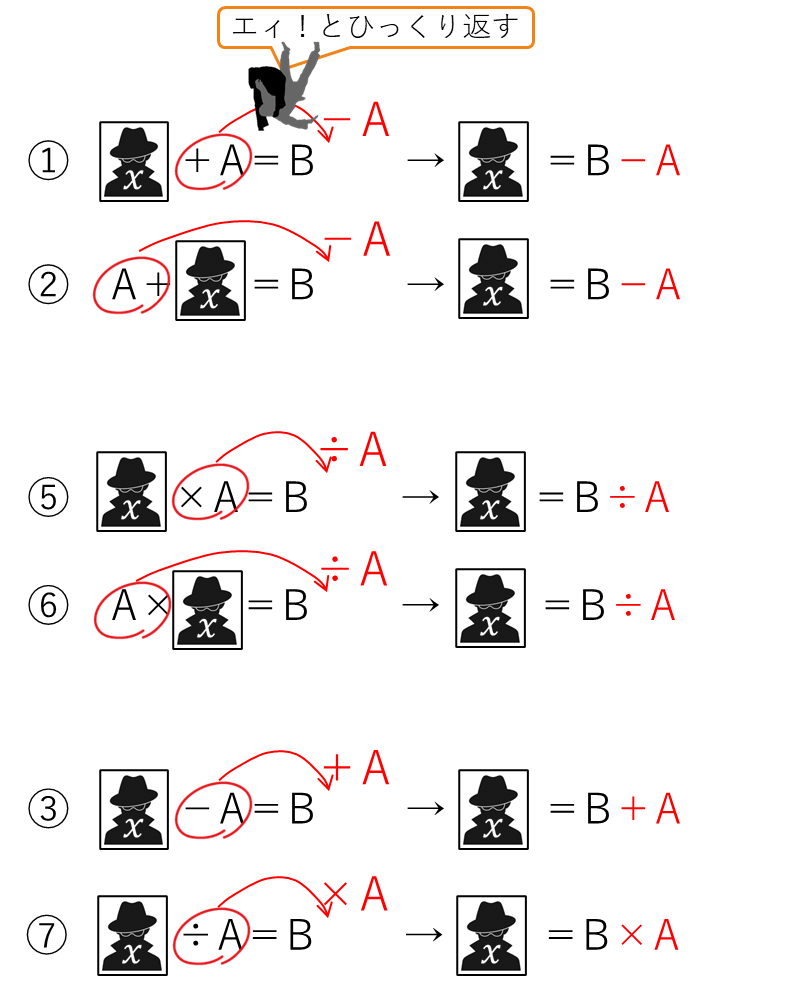
ここで上の図のように、式に直接、ひっくり返す数字に〇をつけて、＝の反対側まで矢印、ひっくり返した演算と数字を書き込んでください。
能力その②－ミスターXがアジトに潜伏していたら（－□，÷□の場合），ろうやにつかまえているミスターXの仲間と交換できる
ミスターXが”－”と”÷”のあとにいる場合（”－□”、”÷□”の場合。「一口、悪口」の場合）は、ミスターXが自分のアジトに隠れてしまって、そのままでは正体がわからない状況です。ここできみの2番目の能力を使って、すでにろうやにつかまえているミスターXの仲間とミスターXを交換して、ミスターXをアジトの外に連れ出してください。
逆算の公式の④と⑧にあてはめると、
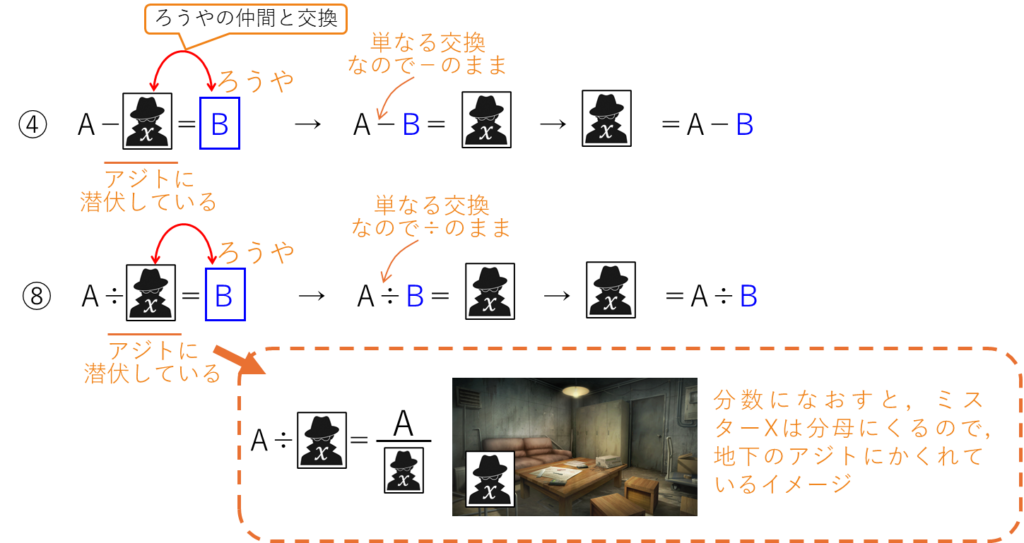
ここでは上の図のように、ミスターX□と交換する数字に、両方向の矢印をかいておくと、直感的にわかりやすくなります。
さあ、きみのこの2つの能力で、ミスターXの正体をあばくことができるようになりました！
基本の例題
式に矢印をしっかりかいて、次の問題を解いてみてください。
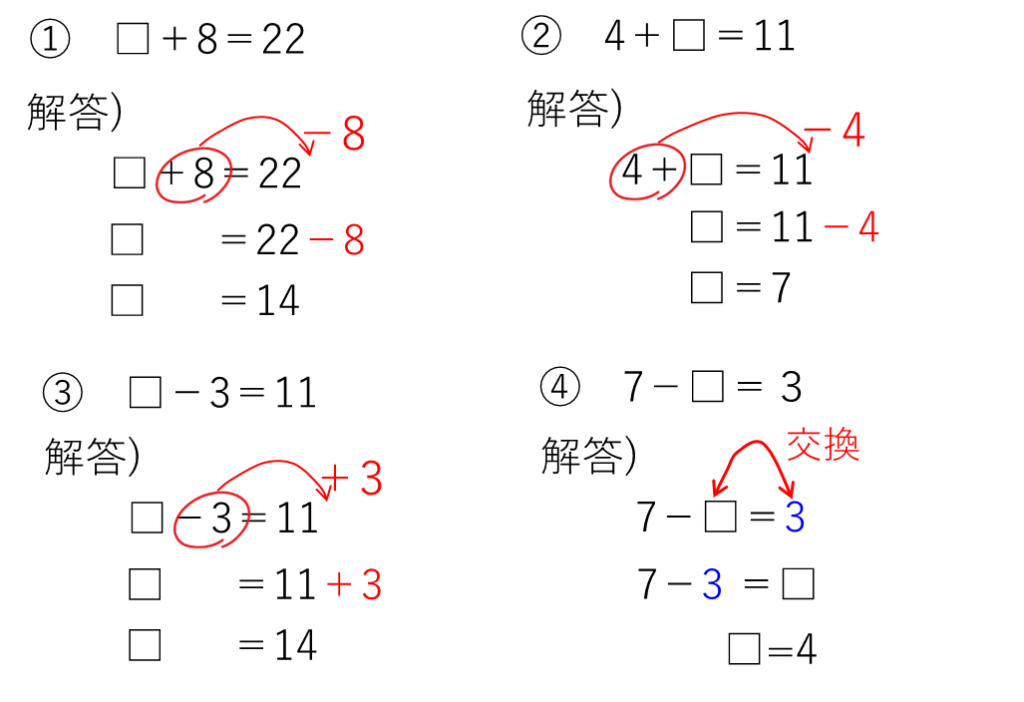
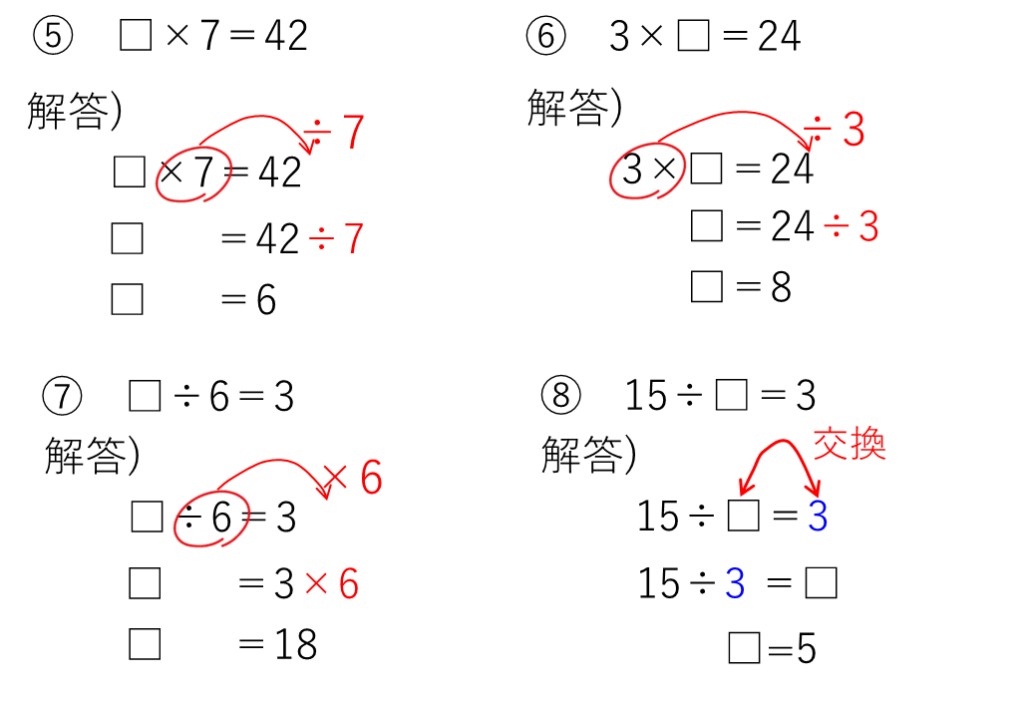
検算
間違ってつかまえてしまったら大問題ですから、本当にミスターXなのか、ちゃんと裏を取っておきましょう。
逆算では、答えをもとの式に入れて計算することで検算が簡単にできます。計算ミスでの失点をなくすためにも、答えをだした後に検算して、確認しておきましょう。
例題①の例
ミスターXの仲間がたくさんいる場合
その①ーミスターXから一番遠い仲間から始末する
ミスターXの仲間がたくさんいる場合もあります。そのときは、ミスターXに気づかれないように、ミスターXから一番遠い仲間から順に始末していきましょう。
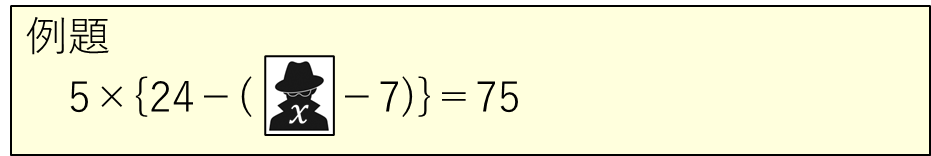
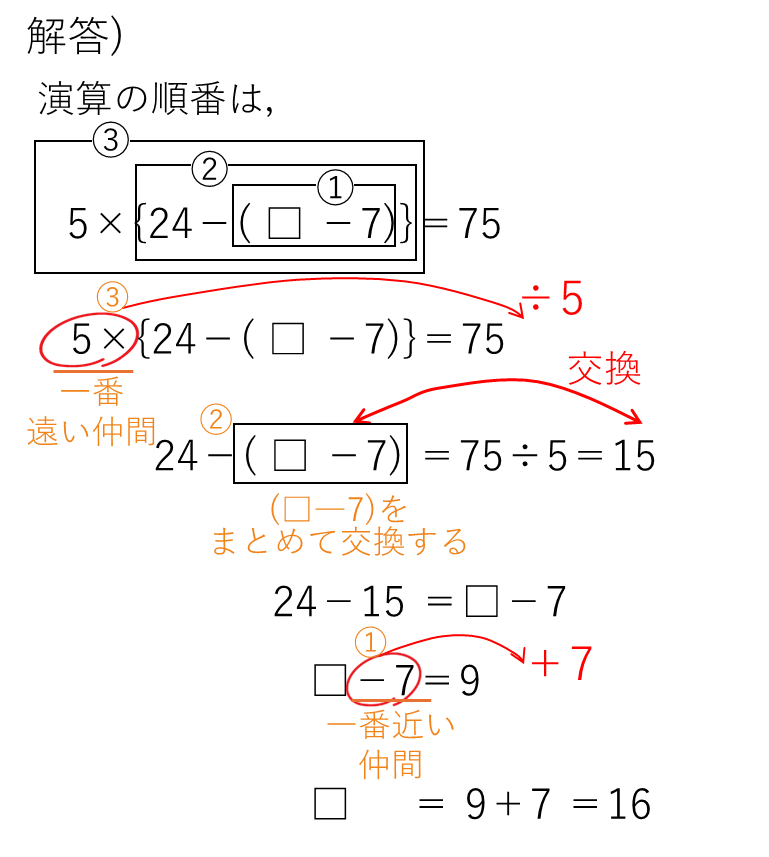
その②ーはじめに仲間をまとめておく
ミスターXの仲間たちを、はじめにまとめてから始末できるケースもあります。
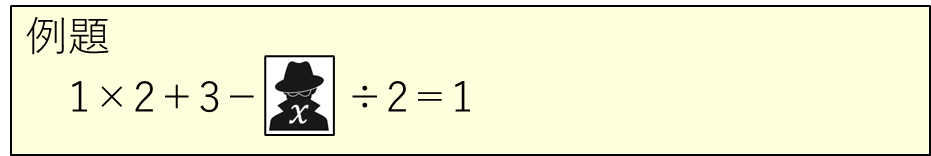
まとめ
今回，逆算の解き方を物語風に説明しました。ミスターXの正体を見やぶることができましたか？
ここで使うワザは２つでした。
〇 ミスターXの仲間をみつけたら、ひっくり返してろうやにいれる
→ たし算＋、かけ算×、□－、□÷の場合は、＋と－、×と÷を入れかえて反対側に持っていく
〇 ミスターXがアジトに潜伏していたら（－□，÷□の場合）、ろうやにいる仲間と交換できる
→ －□、÷□の場合は，□と反対側の値を入れかえる
これらを逆算の公式のように覚えるのではなくて、下のように
と、式に矢印を直接かいて解いていきましょう。これで考える必要はなくなり、機械的に計算することができます。思考がとまることはなくなりますので、あとは計算の順序や小数や分数が混ざっている計算に集中しましょう。
このミスターXの方法で正しく計算できるか疑問に思った場合には、前回説明した線分図や面積図で確認してみてください。
コメント