
「逆算」とは、
わからない数を□として式を作り、□を求める計算のこと
です。入試問題の大問1の計算問題の1つとして出題されることが多いので、計算問題の基本の1つとして確実に解いておきたいですね。
また、特殊算で求めたい数を□とした式をたてて、解いていく場合にも使います。
逆算の公式があり、それを使って解いていくのですが、大問1では,小数と分数が組み合わさった複雑な式もでてきます。公式を確認しながら解くのではなくて計算問題ですから、すらすらと解き進められるようになることを目指しましょう。
2回の連載で、今回は逆算の基本をまとめます。次回は、公式を覚えることなく一瞬で解き進められる方法を教えます。
逆算の基本ルール
逆算の基本ルールは2つです。
- 逆の演算(+⇔-,×⇔÷)を行う
- 逆の順番で演算を行う
逆の演算(+⇔-,×⇔÷)を行う
例)
□+23=61
「+23」の逆の演算である「-23」を行うと
□+23-23=61-23
□=38
逆の順番で演算を行う
例)
(□+25)÷3=12
この式で計算する順番は、

□+25が最初、次に÷3になります。
逆算では,逆になるので,はじめに÷3の逆の×3を行います。
(□+25)÷3×3=12×3
□+25=36
次に、+25の逆の-25を行います。
□+25-25=36-25
□=11
このように,通常の計算とは逆の演算を逆の順に行うので「逆算」と呼ばれるのです。また,演算をさかのぼってもとに戻すので「還元算」とも呼ばれます。
逆算の8つの公式
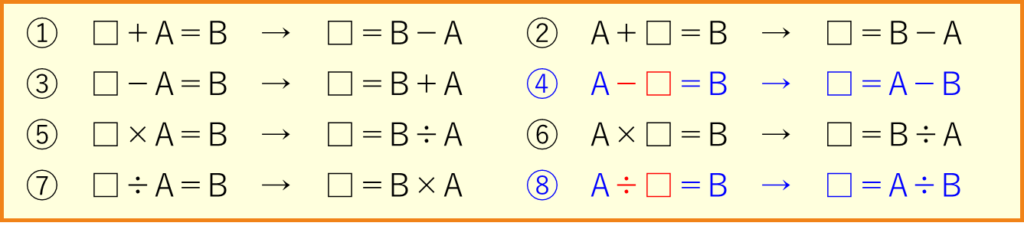
逆算の8つの公式です。この8つの公式を使えば、どんな逆算の問題も解けます。
ここで、④はひき算なのにひき算のまま、⑧はわり算なのにわり算のままなので、注意が必要です。「悪口一口(÷口、-□)」と言って区別すると覚えやすいです。
公式の確認ーたし算
それでは小さい数で公式を確認してみましょう。
① □+A=B → □=B-A
□+2=6
□は、6-2=4になります。線分図にかくと下のようになります。
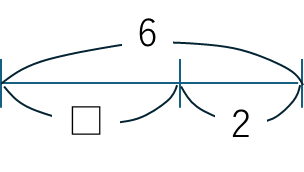
② A+□=B → □=B-A
2+□=6
これも同じように、□は6-2=4になります。線分図も,2と□の位置が変わっただけです。
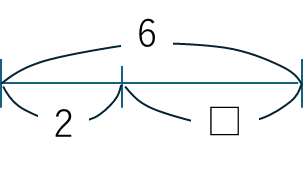
このように、たし算の①と②はたし算の交換法則から
□+A=A+□
となるので,同じように計算できます。
公式の確認ーひき算
③ □-A=B → □=B+A
□-2=6
□は,6+2から8になります。線分図にかくと下のようになります。
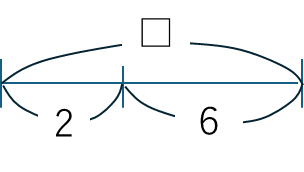
④ A-□=B → □=A-B
6-□=2
この場合、□は6-2=4ですね。③では□は線分図の上(2つ値の和)だったのが,④では下の図のように変わっており,計算の仕方も違っています。
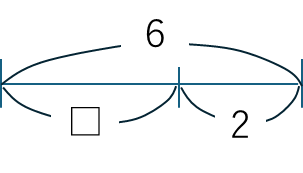
ひき算では交換法則は成り立ちません。Aが等しい場合に③と④の結果は異なります。
□-A≠A-□
したがって,③と④は同じようには計算できません。
公式の確認ーかけ算
⑤ □×A=B → □=B÷A
□×2=6
□は、6÷2から3になります。面積図でかくと下のようになります。
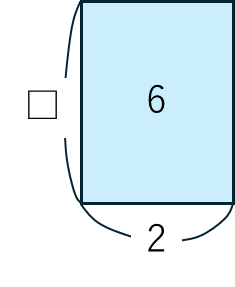
⑥ A×□=B → □=B÷A
2×□=6
これも⑤と同じように、□は6÷2から3になります。
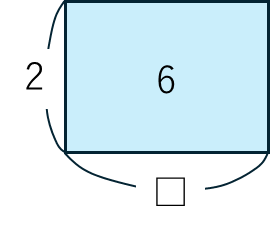
かけ算の交換法則から、⑤と⑥は
□×A=A×□
と等しくなるので、同じように計算できます。
公式の確認ーわり算
⑦ □÷A=B → □=B×A
□÷2=6
□は,6×2から12になります。面積図でかくとすぐわかると思います。
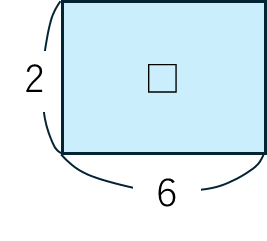
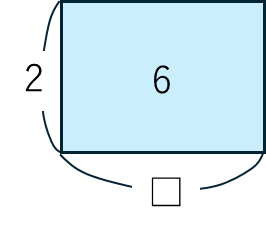
⑧ A÷□=B → □=A÷B
6÷□=2
□は、6÷2から3になります。面積図でかくと下のようになります。⑦では□は2つ値の積だったのが、⑧ではかける数(あるいは,かけられる数)になっているので、計算の仕方も違います。
わり算では交換法則は成り立ちません。Aが等しい場合に⑦と⑧の結果は異なります。
□÷A≠A÷□
したがって、⑦と⑧は同じようには計算できません。
まとめ
逆算のルールと公式を説明しました。公式について理解できたでしょうか?
「-□」と「÷□」 (一口と悪口と覚える)を特別として,ほかの6つは演算を逆にすればよいので覚えやすいと思います。
公式がぱっと浮かばない場合、自信がない場合は、簡単な数字の式を横にかいて解く方法が参考書などで紹介されていますが、計算の途中でいちいち考えていたら複雑な計算を解くことができません。次の回では、逆算の解く方法を物語風に説明して、パッと解き進められるようしていきます。(逆算② 一瞬で解き進められる裏技を教えます!)
コメント