中学受験　算数　覚えておきたい8種類の「数字」

覚えておきたい8種類の「数字」

　ここでは、覚えておきたい8種類の数字、分数と小数の変換、3.14×□、素数、平方数（四角数）、三角数、立方数、$\frac{中心角}{360}$、速さの単位変換をまとめておきます。

分数と小数の変換

　0.25や0.125などの数字は、簡単な分数で表すことができます。小数のまま計算するのではなくて、分数になおすと計算が楽になります。

　分数と小数がまざった計算の例題です。

解答(クリックすると表示)

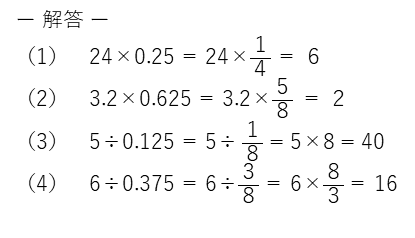
　分数に変えてから計算すると、楽になりますね。

3.14×□

　図形の問題で、円周率として3.14をかける計算は、3けたの小数のかけ算になるのでなかなか大変ですね。3.14×□の計算を、速く、正確に行うために、3.14×□の答えを暗記してしまいましょう。

　3.14×2から3.14×9までのごろ合わせをまとめておきます。

　これだけを覚えておくだけで、あとは筆算を高速に行うことができます。

解答（クリックすると表示)

余裕があれば，問題によく出る

　　3.14×12＝37.68

　　3.14×16＝50.24

　　3.14×25＝78.5

も覚えておきましょう。

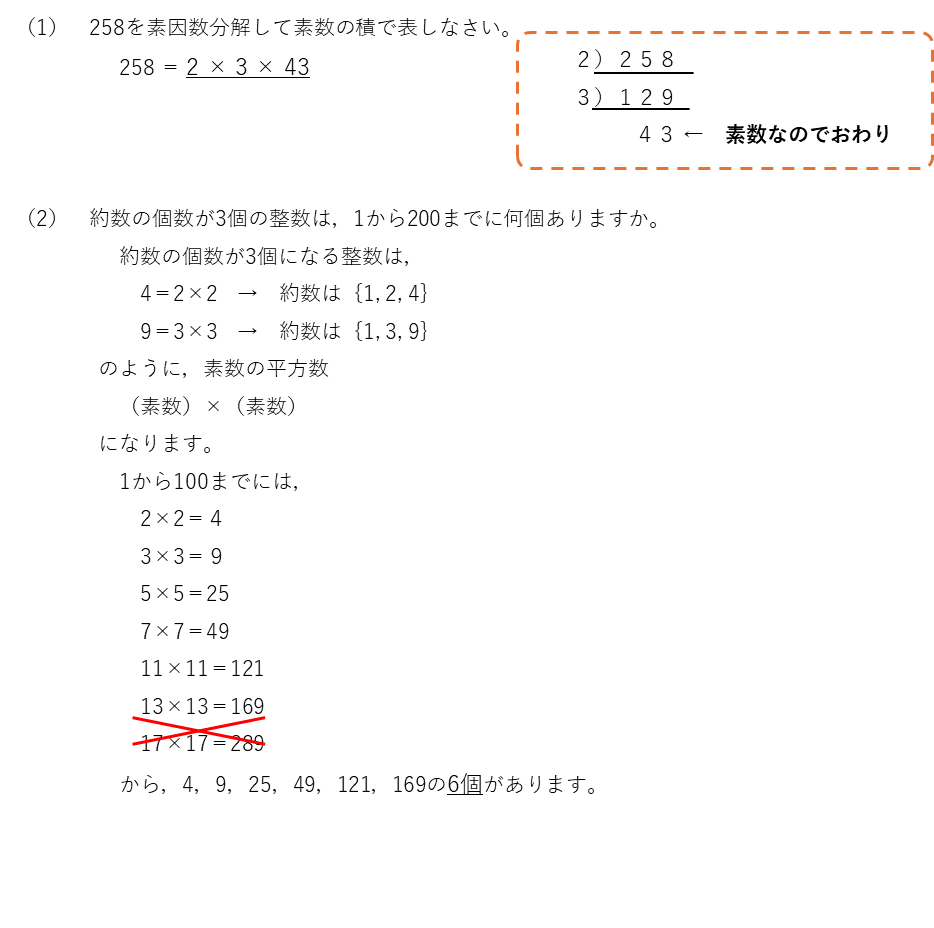
素数

　素数とは、約数が1とその数自身の2個しかない(1以上の)整数です。ここで、1は素数にふくまないことに注意してください。

　素因数分解など素数を使って解く問題や、素数をすべてかき出させるという問題もあります。

　まずは1から30までの素数をしっかり覚えておきましょう。100までは覚えきれないようでしたら、素数の判別方法を使って、見つけられるようにしてください。また、1から50までには15個、1から100までには25個と素数の個数を覚えておくと、かき出した素数にぬけがないかを確認できます。

解答（クリックすると表示）

平方数

　平方数とは、Ｎ×Ｎ（Ｎは整数）で表される整数です。ご石を四角（正方形）にならべたときのご石の個数になるので四角数ともいいます。　平方数は、四角の形にならべた数列や平面図形の相似の問題など問題によく出てきます。

平方数の例）

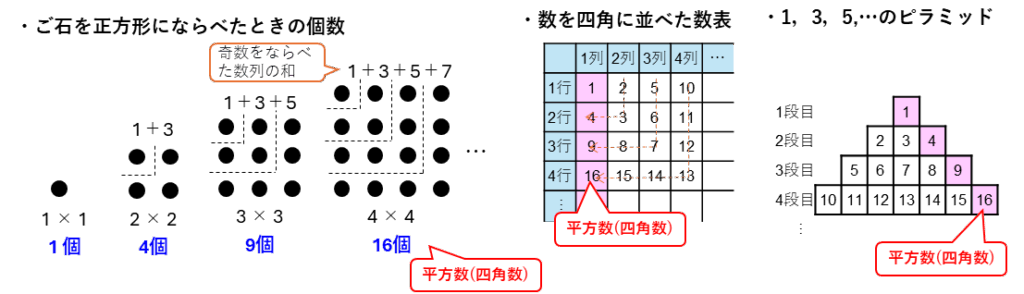
　1+3+5+7+…のように、奇数をならべた数列の和が平方数（四角数）になっています。

　1×1～9×9は九九にでてくるので自然と覚えていると思います。10×10=100も大丈夫でしょう。できれば、その続きの11×11～19×19までを覚えてください。

　平方数が出てくる例題を2つのせておきます。

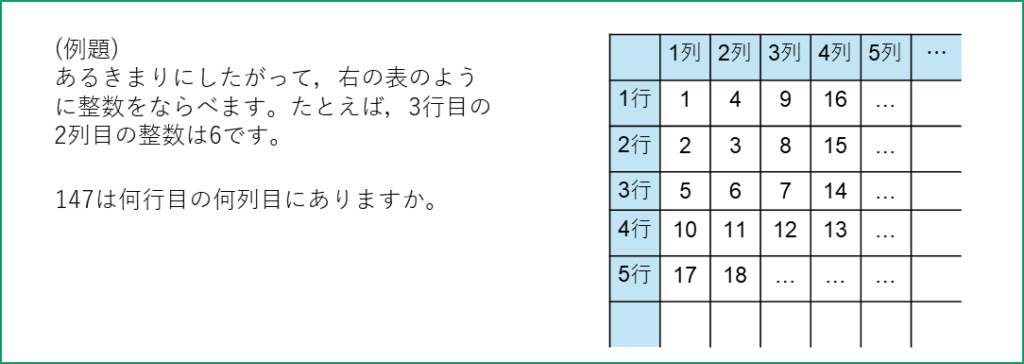
解答（クリックすると表示）

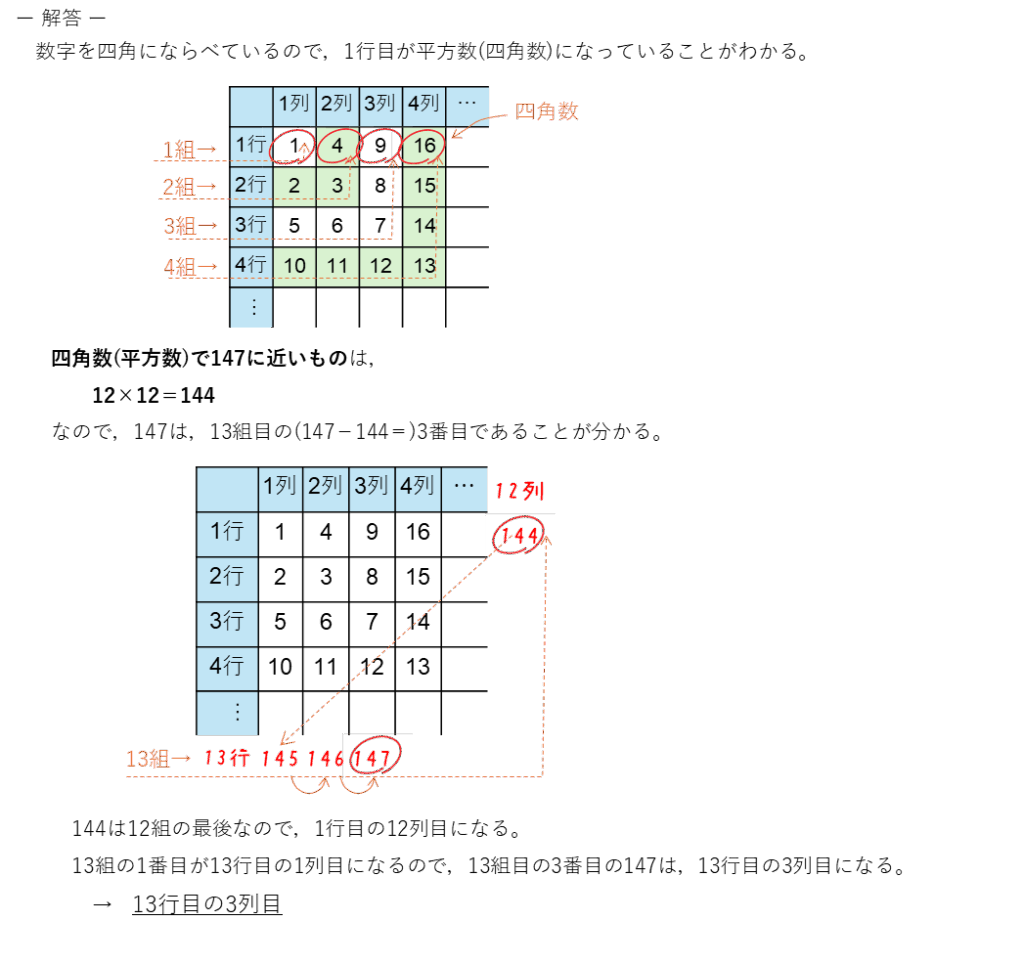
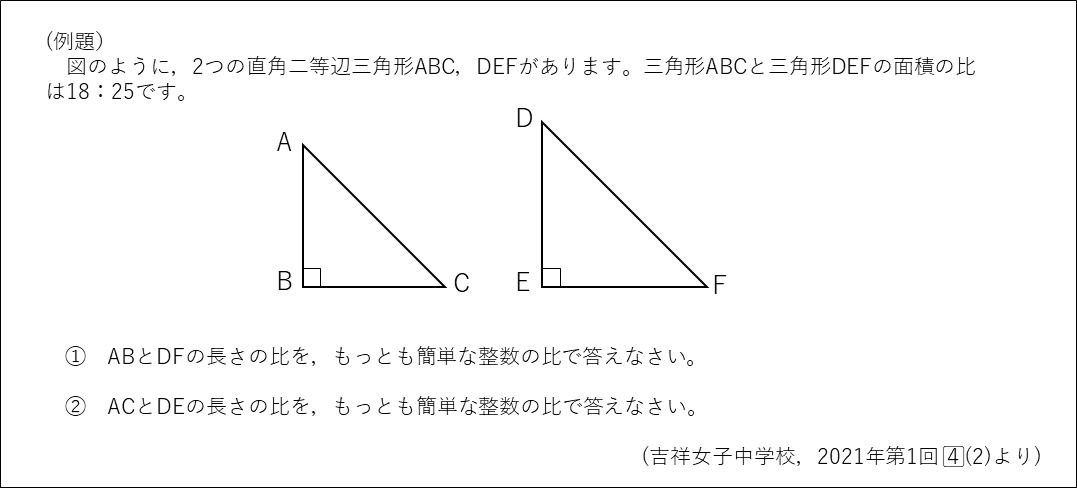
解答（クリックすると表示）

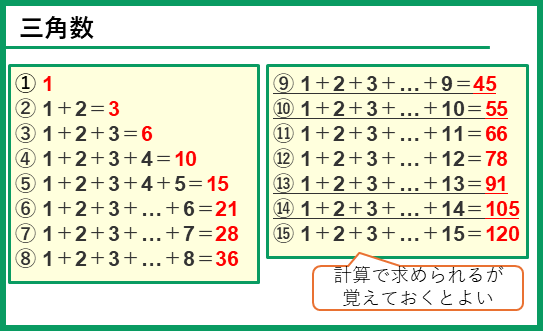
三角数

　三角数とは、1+2+3+4+…のように１から連続した数列の和です。ご石を正三角形にならべたときなど、数を三角の形にならべたものです。

三角数の例）

　

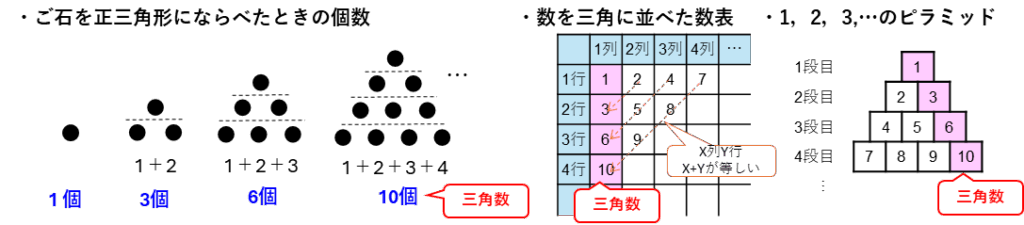
　Ｎ番目の三角数は、1+2+3+…+Ｎになるので、等差数列（はじめの数1、公差（加える数1））の和で求められます。

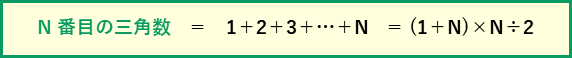
　これを理解しておけば計算で求めることができますが、覚えておくと問題を解くのが楽になることがあります。特に、10番目の三角数は(1+2+…+10)なので55、100に一番近いのは14番目の三角数(105)あたりをしっかりおさえておきましょう。

立方数

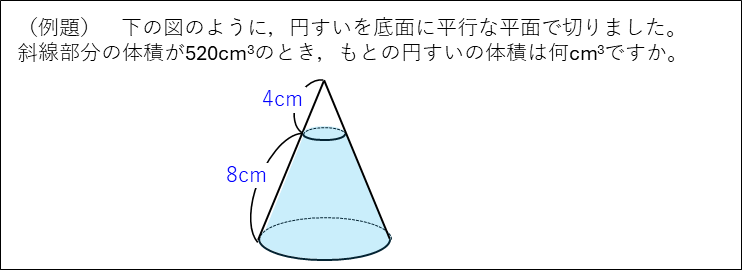
　立方数とは、Ｎ×Ｎ×Ｎ（Ｎは整数）で表される整数です。平方数が平面図形（特に、正方形や直角二等辺三角形の面積比）で出てくるのに対して、立方数は立体図形の体積比でよく出てきます。

　三角すい台、プリンのような形の円すい台の体積を求める問題では、立方数をつかって体積比で考えると計算が楽になります。立体数を覚えて比で考えられるようにしましょう。

解答（クリックすると表示）

中心角／360

　おうぎ形の面積や弧の長さを求めるときに、円の面積や円周に$\frac{中心角}{360}$をかけて計算します。$\frac{中心角}{360}$が簡単な分数になる角度を覚えておきましょう。

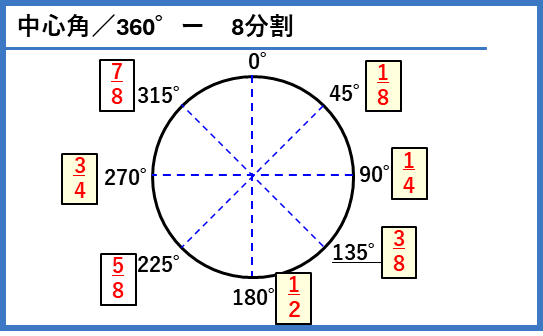
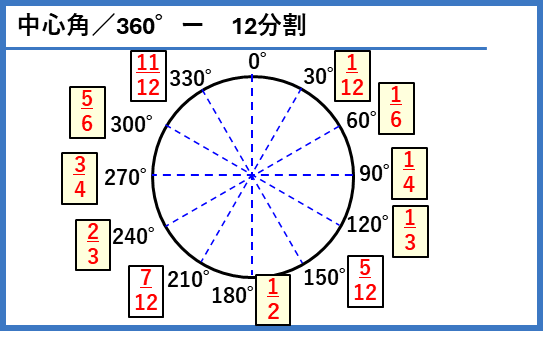
　円を12分割したときは、時計の1時間ごとの目盛りに対応しています。

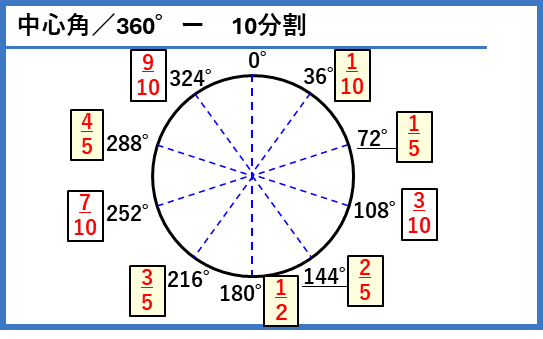
解答（クリックすると表示）

速さの単位変換

　通過算では、速さの単位を時速と秒速で変換する必要があります。よく問題に出る数字を時速□kmと秒速□mの変換の式と一緒に覚えておくとよいです。

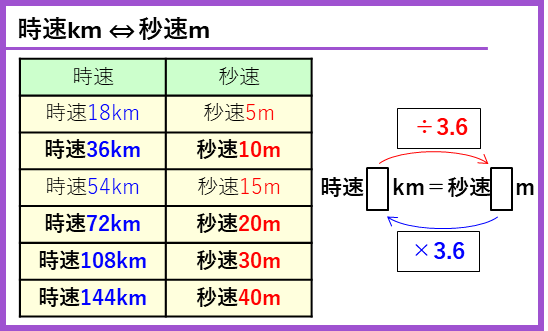
速さの変換は、次のように考えられます。

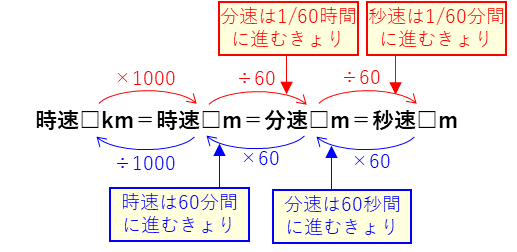
　分速をとばして考えると、

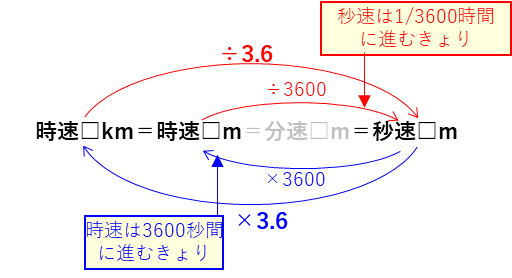
となるので、

　時速□kmから秒速□mへの変換では÷3.6

　秒速□mから時速□kmへの変換では×3.6

すればよいです。

まとめ

　8種類のカードを1枚にまとめておきます。Ａ４等倍で印刷すれば、名刺サイズになりますので、切り分けてカードとして活用することもできます。