
おだんご図で解く特殊算ー差集め算(過不足算)・つるかめ算・弁償算・とりちがえ算
差集め算(過不足算)
差集め算は、2種類のものが同じ数だけあった場合に、1つあたりの差の合計(つまり、差を集めたもの)が全体の差と等しくなることを使って個数を求める問題です。あまりや不足から全体の差を求めてから解く問題を、特に過不足算ということもあります。
差集め算の基本ー2本の串だんごの図
次の例題を考えてみましょう。

まずは、この問題のおだんご図をかきます。
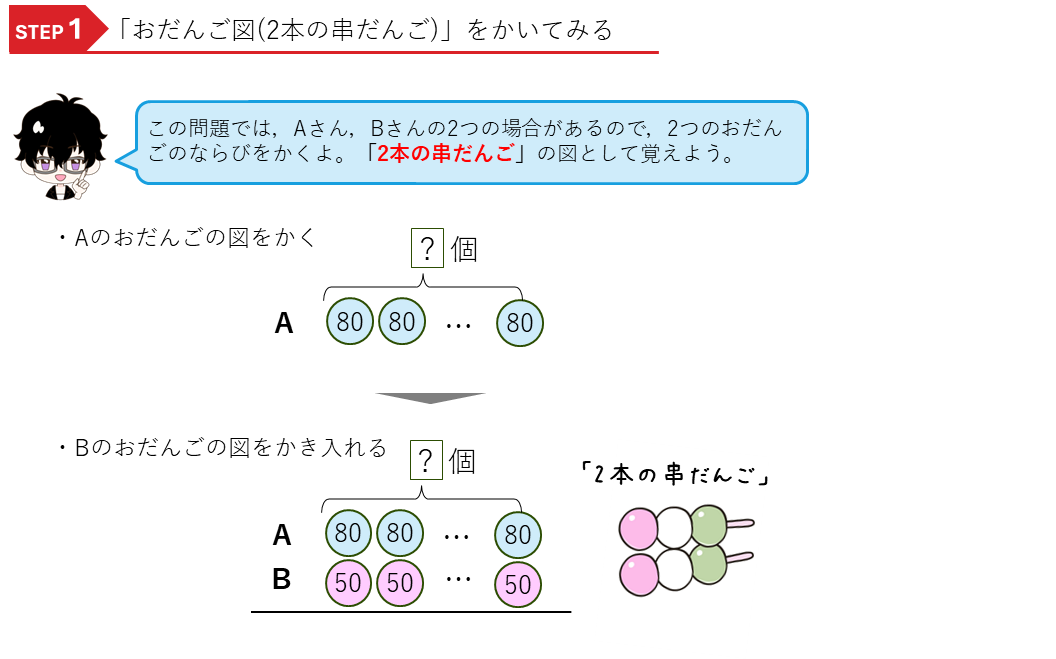
次に、差を考えます。
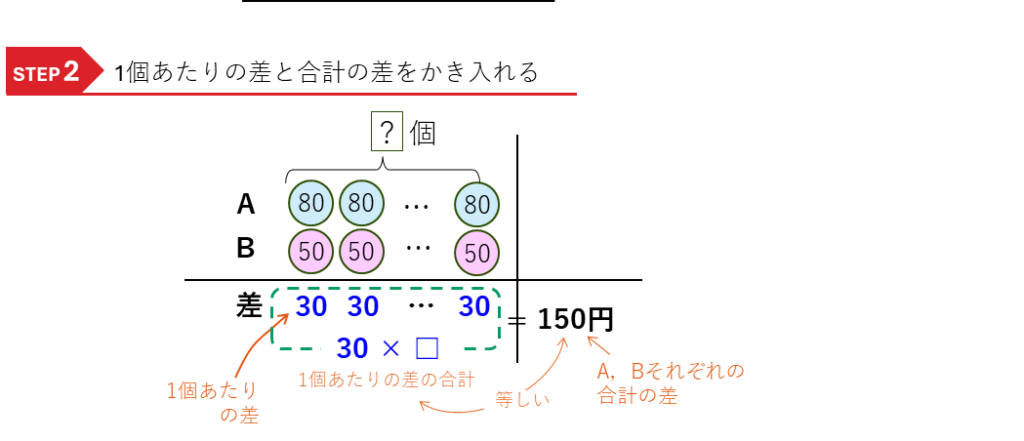
最後に、だんごの数を求めます。

このように、差集め算では”2本の串だんごの図”をかいて、差の合計から解くのがポイントです。

では、次に、あまりと不足がある差集め算(過不足算)の例をおだんご図を使って解いてみましょう。
あまりと不足がある差集め算(過不足算)

この問題では、まず、線分図をかいて「あまりと不足の差」が「全体の差」になっていることを確認してみましょう。
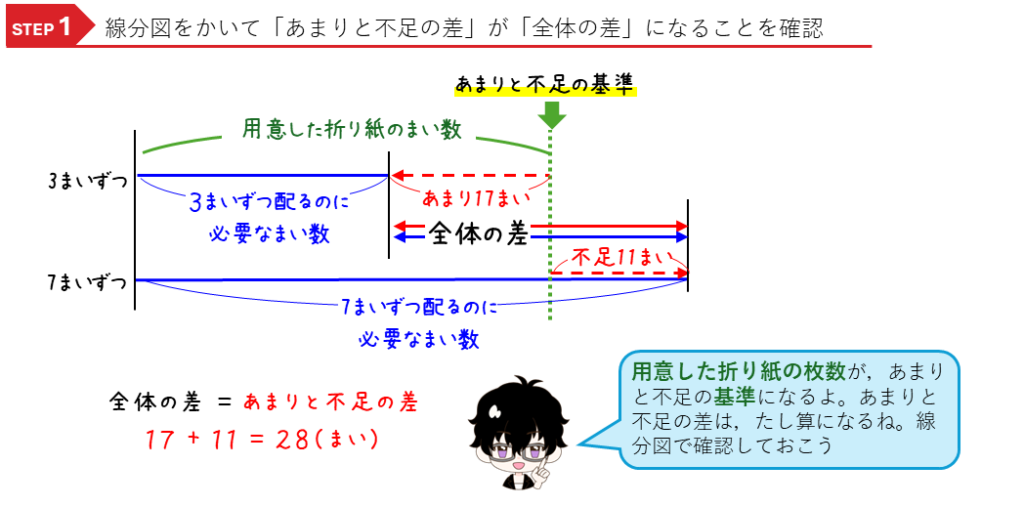
次に、おだんご図をかきます。この問題では、3まいずつと7まいずつの2つの場合があるので、2本の串だんごの「おだんご図」をかきます。

この図に差をかき入れます。

ともに「全体の差」になるので、1人あたりの差の合計(4×□人)が、あまり・不足の差28と等しくなることが分かります。ここから、子どもの人数を求めることができます。

このようにあまりと不足がある差集め算では、あまりと不足の差が全体の差になるので、次の式から求めたい個数を計算できます。

おだんご図をかけば自然とこの式がでてきます。公式にあてはめて解けたとしても、公式なんてしばらくすると忘れてしまいます。公式として覚えるのではなくて、図をかいて解けるようにしましょう。
つるかめ算
つるかめ算については,面積図を使った解法も紹介しています(面積図で解こう!②-つるかめ算とその仲間たちを分かりやすく解説)が,ここではおだんご図を使った解法を説明します。面積図のところで説明していますが、弁償のつるかめ算(弁償算)では面積図がうまく使えないので、普通のつるかめ算もおだんご図を使って解くことを理解しておきましょう。
つるかめ算の基本問題

・つるは、1羽あたりの足の数が2本
・かめは、1匹あたりの足の本数が4本
と,1つあたりの数が2種類ある問題です。
つるかめ算つるかめ算では、みんな”つる”、あるいは、みんな”かめ”のように、どちらか一方にみんなおきかえた場合を仮定して、この場合と実際との差を考えて解きます。こでは、みんな”かめ”として考えます。(問題では”つる”が何羽か聞いているので、反対の”かめ”にすべておきかえます。)
では、みんなかめと実際の2つの串だんごの図をかいていきましょう。
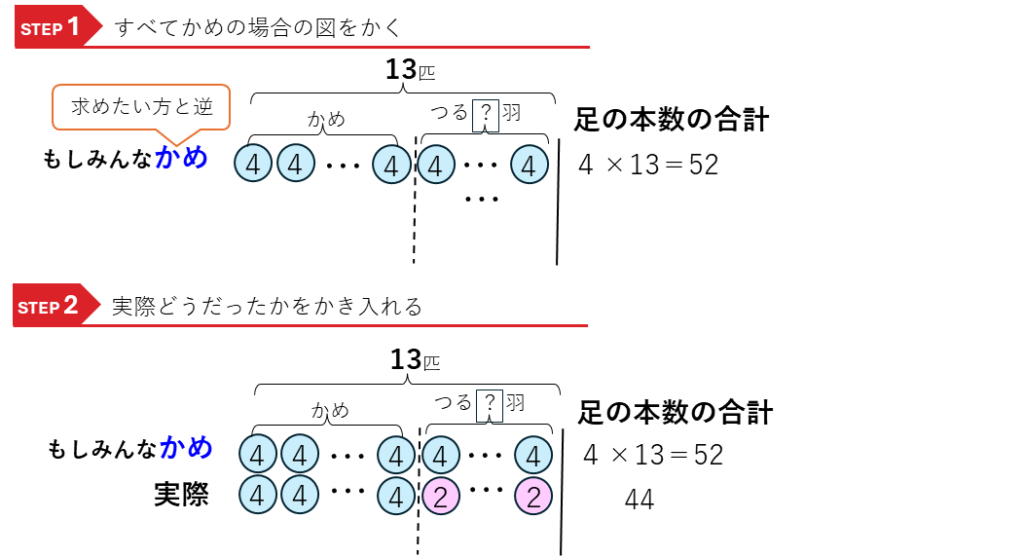
次に、差をかき入れます。
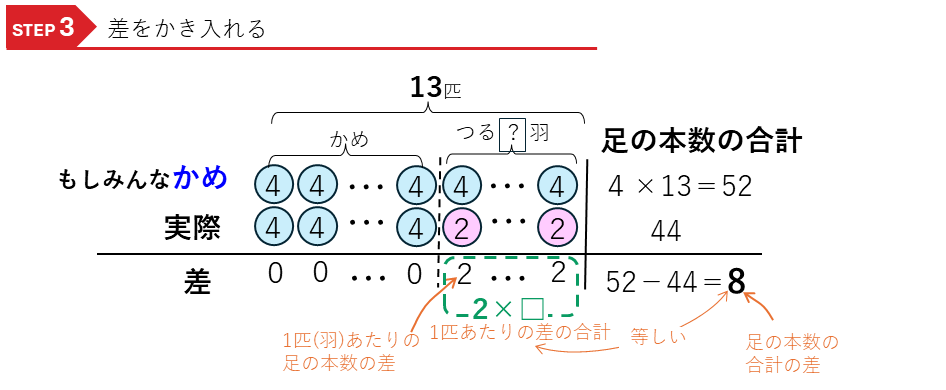
差集め算と同じように、足の本数は、1匹あたりの差の合計がつるとかめそれぞれの合計の差と等しいことから,つるの数を求めることができます。

このように、つるかめ算では、「もしみんな”〇〇”だったら」と、一方にすべておきかえた場合を考えることで、差集め算と同じようにおだんご図をかいて解くことができます。
弁償のつるかめ算(弁償算)
次に、弁償のつるかめ算(弁償算)の問題を解いてみます。(4年上 第18回 一方におきかえて解く問題での解説と同じです。)

この問題のように、弁償の問題では、お皿を洗うと20円もらえ、わってしまうと50円はらうというように、もらうとはらうの2つがある問題です。次のように、おだんご図をかいて解いていきます。
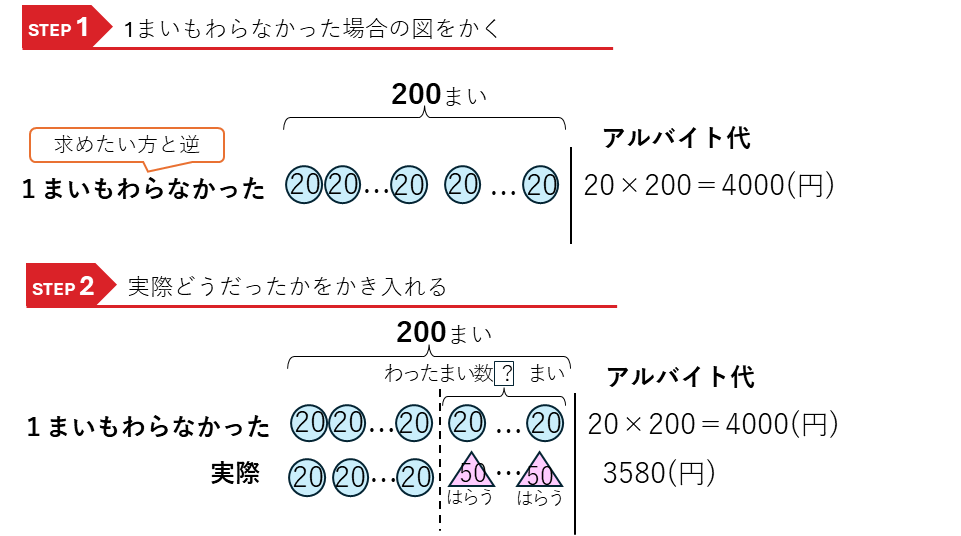
実際にアルバイト代としてもらった金額は3580円です。何枚か、わってしまったので、そこは50円はらうことになる。もらうと区別するために△にしてかきましょう。
では、この2つの場合の差をかき入れて、わったお皿の枚数を求めましょう。
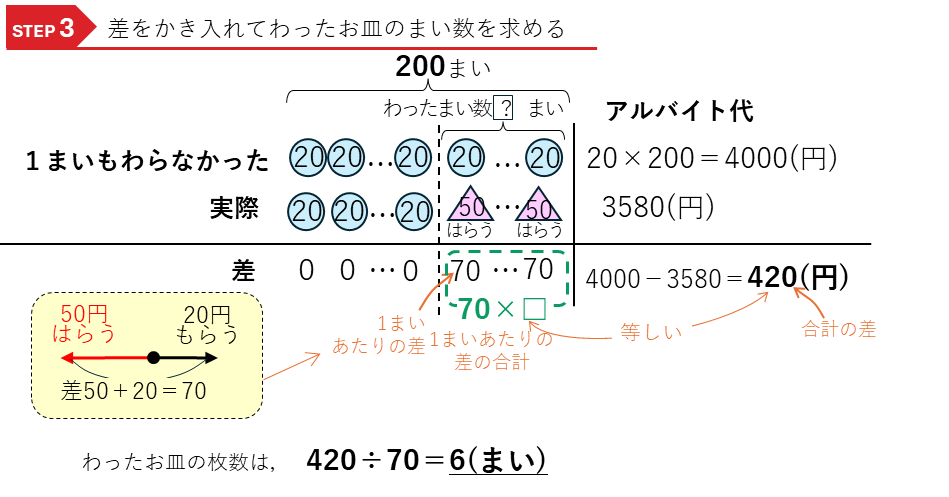
全体の差は、4000-3580=420(円)となります。1枚当たりの差は、洗うと20円もらえ、わってしまうと50円はらうので、70円になる。ここが弁償算のポイントです。
したがって、わったお皿の枚数は、
420÷70=6(枚)
となります。
とりちがえ算
おだんご図の最後は、とりちがえの問題(とりちがえ算)です。とりちがえの問題は、AとBを買うときに買うまい数をまちがって逆にしてしまったというものです。次の例題を考えてみます。

とりちがえの問題では、まず、どちらを多く買ったのかをはっきりさせます。

予定ではチョコレートの方を多く買うはずでしたが、実際にはガムを多く買ってしまったことが分かったので、これを「おだんご図」でかいてみます。

このように、とりちがえ算では予定と実際でそれぞれ2本、合計で4本の串だんごの図をかきます。次に、代金の差から、ガムとチョコレートの個数の差を求めます。
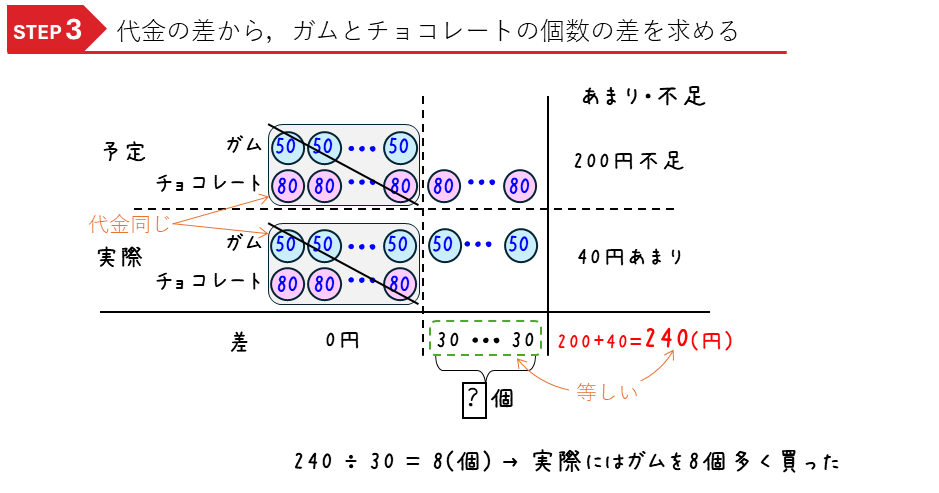
このように、予定と実際の両方で、ガムとチョコレートを同じ数だけ買ったところは差として消えることが図から分かるので、ガムとチョコレートの差のところだけに注目して解くことができます。
おだんごで解く特殊算のまとめ
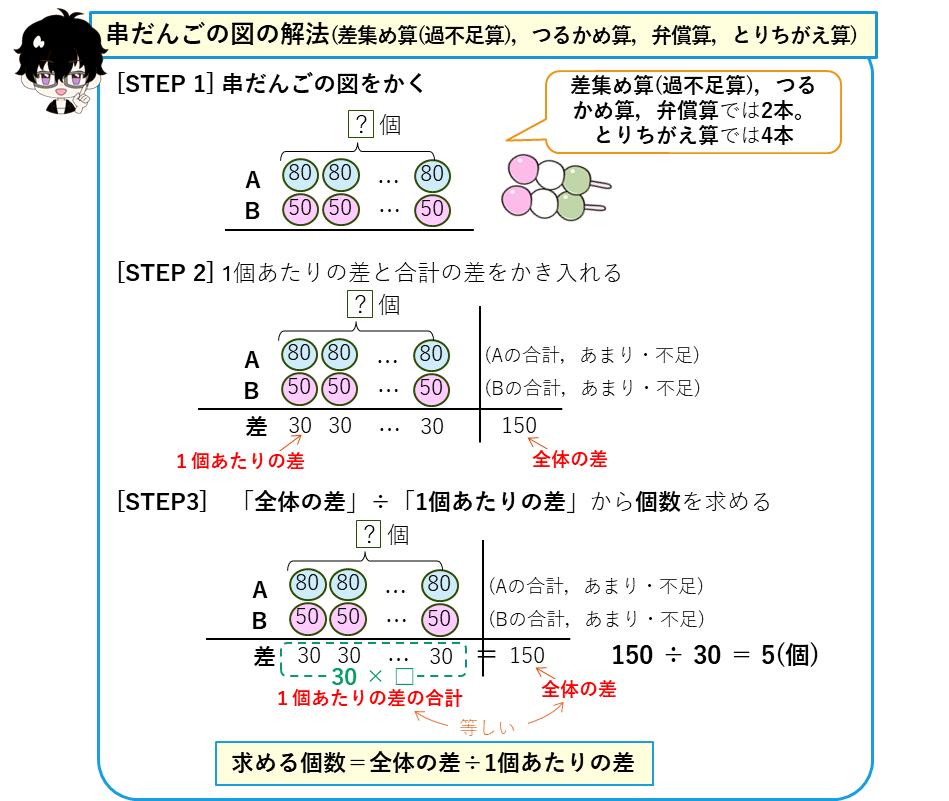
おだんご図(串だんごの図)で解く、差集め算(過不足算)、つるかめ算、とりちがえ算の解法をまとめます。2つの場合のおだんご図をかいて、全体の差と1個あたりの差が明らかになるので、
求める個数=全体の差÷1個あたりの差
から、個数を求めることができます。
おだんご図のメリット
おだんご図には、次のメリットがあります。
・ パッと見て分かりやすい(と思う)
・ 1個(1人)あたりの差が図にならんでかかれるので、「1個(1人)あたりの差の合計」が「全体の差」になることが分かりやすい
・ 個数をそろえることを強く意識できる(特に、個数がちがう差集め算(過不足算)で重要)
・ 弁償算、とりちがえ算は、おだんご図でないと解けない(面積図でかくのが難しい)
一方で、差集め算(過不足算)において、「あまり・不足の差」が「全体の差」であることや、あまりと不足の差がたし算になること、あまりとあまりの差や不足と不足の差がひき算になることが、図からは直接的には分かりません。この点については、線分図などで理解した上でおだんご図を使いこなせるようにしましょう。
コメント